Modelling shock drift acceleration of electrons at the reconnection outflow termination shock in solar flares

A. Warmuth; G. Mann; H. Aurass

doi:10.1051/0004-6361:200810101

Free Access

Issue		A&A Volume 494, Number 2, February I 2009


Page(s)		677 - 691
Section		The Sun
DOI		https://doi.org/10.1051/0004-6361:200810101
Published online		03 October 2008

Observational constraints and parametric study

A. Warmuth - G. Mann - H. Aurass

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 30 April 2008 / Accepted 18 September 2008

Abstract
Context. The acceleration of electrons to nonthermal energies in solar flares is one of the main unsolved questions in solar physics. One possibility for producing these energetic electrons is acceleration at the reconnection outflow termination shock (TS).
Aims. By comparing theoretical results with observations of nonthermal electrons, we determine whether shock drift acceleration (SDA) at the TS is a viable electron acceleration mechanism.
Methods. We used radio observations to constrain the characteristics of the TS, and hard X-ray observations provided by RHESSI, INTEGRAL, and HXRS to obtain the characteristics of the injected electrons. Invoking relativistic shock-drift acceleration at the TS, we calculated electron flux spectra, which are then compared with the corresponding observational results from RHESSI. A parametric study of the model allows us to answer the question under which conditions the TS is a viable electron accelerator.
Results. SDA at the TS is able to reproduce the required fluxes and kinetic power of nonthermal electrons in solar flares as long as there is significant heating of the outflow jet and a sufficiently large shock area. A prediction of the model is that the flux and power of injected electrons is higher than the values that are usually given by fitting observed spectra, since the low-energy cutoff is generally below 10 keV. The synthetic spectra are consistent with the observed spectral indices up to $\approx$ 100 keV. Beyond that, they soften too quickly. Possibly this is because we have not yet considered various additional effects, such as multiple reflections at the shock or some form of preacceleration. The observed relation between electron flux and spectral index is reproduced by the model, as well as the temporal evolution of the energetic electrons. We conclude that SDA at the TS is a viable electron acceleration mechanism that deserves further study.

Key words: Sun: flares - Sun: corona - Sun: radio radiation - Sun: X-rays, gamma rays - shock waves - acceleration of particles

1 Introduction

During solar flares a large amount of energy originally stored in coronal magnetic fields is suddenly released and converted into thermal energy of heated plasmas, bulk mass motions (such as flare sprays or coronal mass ejections), and accelerated particles (electrons, protons, and heavier ions). Studies of the energetics of these different components have shown that nonthermal electrons carry a significant fraction of the total energy released (e.g. Lin & Hudson 1976; Emslie et al. 2005). Therefore it is imperative to understand the acceleration mechanism of these energetic electrons.

The generation of nonthermal electrons (and ions) is still one of the main unsolved questions in solar physics. There are several demanding requirements for any potential acceleration mechanism: it must be able to accelerate a large number of electrons to high energies at sub-second timescales. The currently discussed models generally fall into three categories: direct-current (DC) acceleration (e.g. Holman 1985; Benz 1987; see Litvinenko 2003, for a review), where electrons are accelerated in large-scale electric fields, stochastic acceleration, where electrons gain energy from turbulent waves (e.g. Melrose 1994; Miller et al. 1997), and finally shock acceleration, where electrons are reflected and accelerated by a shock wave (e.g. (Holman & Pesses 1983; Mann et al. 2001).

While the nature of the acceleration mechanism is still vigorously debated, it is widely accepted that the process is taking place within the magnetic reconnection scenario of solar flares. In a two-ribbon flare, for example, an erupting prominence leads to the close contact of oppositely-directed underlying magnetic field lines. At this point, the onset of anomalous resistivity can lead to the formation of a diffusion region (DR) in which the oppositely-directed magnetic field lines can reconnect. Due to their curvature, the newly-formed field lines have a strong magnetic tension and are thus rapidly propagating away from the DR, taking the plasma with them. In this manner, two reconnection outflow jets are formed. Outflow jets have recently been identified in SOHO/SUMER spectra (Wang et al. 2007).

The outflow is separated from the inflow by two pairs of slow-mode standing shocks (SMS) that are attached to the DR. The inflowing plasma is heated at these shocks. If the outflow is supermagnetosonic, a fast-mode standing shock (FMS), also called termination shock (TS), is formed at the transition between super- and submagnetosonic propagation. Such a transition must necessarily occur for the downward jet (the lower TS), and may also occur for the upward one (upper TS). Somewhere within this configuration, particles are accelerated, which then propagate down along the magnetic field lines until they reach the dense chromosphere where they generate thick-target hard X-ray (HXR) radiation (Brown 1971) and are finally thermalized.

While the ``central ingredients'' of both DC and stochastic acceleration - large-scale electric fields and small-scale turbulence - cannot be directly observed, fast-mode shocks can be observed due to the plasma radiation they generate, which is seen in dynamic radio spectra as type II bursts (e.g. Nelson & Melrose 1985). It is well-established that energetic particles can be produced by moving coronal and interplanetary shocks which are driven by coronal mass ejections (CMEs). As we have seen, fast-mode shocks suitable for particle acceleration can also be found in solar flares: the TS is a standing fast-mode shock at which particles could be accelerated. This possibility was first suggested by Tsuneta & Naito (1998).

For a long time, the TS has remained a theoretical concept (e.g. it was found in numerical simulations by Forbes 1986; Shibata et al. 1995), however, we now have evidence from radio observations that it actually exists in solar flares (e.g. Aurass et al. 2002, see also Aurass 2007, for an overview). Prompted by these observations, we study quantitatively if acceleration at the TS could be a viable electron acceleration mechanism by combining HXR and radio data with modeling. The advantage of this approach is that radio data constrain several vital parameters of the accelerator (e.g. ambient density at the shock), something which is not possible for other scenarios.

The acceleration is modeled with a fully relativistic shock drift mechanism, which has been developed by Mann et al. (2006) and Mann et al. (2009, henceforth Paper I). While the focus of Paper I was on deriving a relativistic theory of SDA and comparing the model output with a single large event, this work will study systematically how the model output changes as a function of the input parameters and how this compares to observations. In short, we will study how well the SDA model fulfills the observational constraints.

The radio and HXR observations constraining our model will be discussed in Sect. 2. The model of electron acceleration based on SDA will be reviewed in Sect. 3 (for further details, see Paper I), and a parametric study of this model will be discussed in Sect. 4. The conclusions will be drawn in Sect. 5.

2 Observational constraints

Our model of SDA at the TS is constrained from two sides. On the one hand, radiospectral and radioheliographic observations provide information on some of the model parameters. On the other hand, HXR data are used to derive the accelerated electron fluxes, which are then compared with the results given by the model. This allows us to determine under which conditions SDA at the TS can be considered as a viable electron acceleration mechanism.

2.1 Constraints on the TS from radio observations

In dynamic radio spectra recorded with the radiospectropolarimeter in Tremsdorf (Mann et al. 1992) we have observed radio signatures that have all the characteristics of metric type II bursts (see e.g. Nelson & Melrose 1985), including narrow bandwidth, bandsplitting and fine structures such as herringbones. It is generally accepted that type II bursts are generated by shock waves propagating outwards through the corona. This results in emission lanes drifting from higher to lower frequencies. However, the features we observed show no or only weak drift with frequency (see Aurass et al. 2002). It is reasonable to assume that also these non-drifting bursts are generated by coronal shock waves, just like the normal type II bursts are. Moreover, the Nançay Radioheliograph (NRH; Kerdraon & Delouis 1997) shows that the corresponding radio sources are stationary (e.g. Aurass et al. 2006). Thus, the radio emission must be caused by a standing shock wave. Since the radio source is always located close to a flaring active region (AR), we interpret these radio features as signatures of the TS. In one event, signatures of both a lower and an upper TS were observed (Aurass & Mann 2004). The fluxes of these two features were anticorrelated, which is actually predicted by numerical simulations of magnetic reconnection (Forbes 1986). This is a strong indication that the observed radio burst features really are signatures of a TS, and not some other physical phenomenon.

In three of the five events that have been conclusively identified (see Aurass 2007), radio signatures of the TS are visible only after the impulsive phase of the flare. In case the TS actually did not exist during the impulsive phase, it would no longer be a candidate for the acceleration of the bulk of the nonthermal electrons, but could still be responsible for the continuous heating that is needed in the late phase of long-duration flares (e.g. Harra-Murnion et al. 1998). However, a TS signature will be more difficult to observe during the impulsive phase, when other kinds of radio emission features are present (e.g. type III bursts, type IV continua) which can obscure a TS signature. Moreover, the impulsive phase is accompanied by violent plasma motions and probably bursty reconnection. Thus, no smooth and homogeneous shock will be created, instead it will be highly fragmented in space and time. This will wash out characteristic TS signatures such as narrow bands or fine structures, ultimately leading to a nondescript continuum emission.

These issues imply that it is not possible to determine how frequently termination shocks are present in solar flares. All that can be said is that clear signatures of TS are rather rare. Between 1997 and 2003, we have conclusively identified the five events mentioned above through simultaneous high-resolution radiospectral observations with the Tremsdorf instrument and imaging data from NRH. Several tentative TS events were observed with the Tremsdorf spectrograph only. However, we have not completed the search for TS events in our database yet, so these values should be considered as lower limits for the occurrence of clear TS signatures.

In certain events the conditions may nevertheless be just right so that even during the impulsive phase a TS signature may be detected. This was the case for the X1.7 flare of 2001 Mar. 29 (Aurass 2007) and the huge X17 flare of 2003 Oct. 28 (Aurass et al. 2006; Mann et al. 2006; Mann et al. 2009). The latter event is particularly intriguing: a comparison of the radio data with HXR and $\gamma$ -ray count rates provided by the SPI spectrometer aboard the INTEGRAL satellite (see Gros et al. 2004; Kiener et al. 2006) shows an excellent temporal correlation, as shown in Paper I.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig1.eps}\end{figure}$

Figure 1:

Top: dynamic radio spectrum (Tremsdorf radiospectrograph) showing the impulsive phase of the X1.7 flare of 2001 Mar. 29. Around 300 MHz a slowly drifting TS signature is visible starting at 10:04 UT. Bottom: HXR count rates in the energy channels (from above) 67-100, 100-147, and 147-220 keV as given by the HXRS instrument for the corresponding time range. Note the temporal correlation with the TS signature.

Open with DEXTER

A similar correlation is found for the event of 2001 Mar. 29: Figure 1 shows a dynamic radiospectrum of the impulsive phase and the HXR count rates in the energy channels 67-100, 100-147, and 147-220 keV as observed by the HXRS instrument for the corresponding time range. HXRS is a scintillation counter spectrometer with 8 energy bands covering the range 13-500 keV (see Fárník et al. 2001). Before 10:04 UT, we note a gradual rise of the HXR count rate, which is significantly increased with the appearance of the TS signature around 300 MHz between 10:04 and 10:05 UT. Note that in this event there is a slight drift of the TS signature, corresponding to speeds below 300 km s^-1. Starting at 10:09, the TS signature becomes obscured by broad-band type IV emission (during this time, the HXR fluxes show a second maximum). This clearly demonstrates that in many events any TS features will swamped by other kinds of emission during the impulsive phase. After the type IV burst, which ends at 10:12 UT, a feature which is probably the continuation of the TS signature is observed below 170 MHz for an additional minute. During this time, the HXR flux quickly decreases and returns to background levels. In summary, the timing suggests that the TS might indeed play an important role in the acceleration of the bulk of the energetic electrons.

In addition to motivating the study of acceleration at the TS in the first place, radio observations can be used to derive several important shock parameters. Most importantly, since the TS signature is due to plasma emission, the electron density N₀ upstream of the shock can be obtained from the frequency at which it is observed. TS signatures have been observed in the range of 125-390 MHz. Only in the case of 2003 Oct. 28 we can unambiguously determine N₀, since this has been the only event where both the fundamental and harmonic emission lanes were detected. In this case, $N_0=3~\times~~10^8$ cm^-3 is found. Assuming fundamental or harmonic emission for the other events, density ranges of $N_0=7 \times 10^8$ - $2 \times 10^9$ cm^-3 and N₀=1.7- $5~\times~~10^8$ cm^-3 are found, respectively.

The increase of the magnetic field strength at the shock, $X=B_{\rm down}/B_0$ , can be estimated from the amount of band-split (Mann et al. 1995; Vrsnak et al. 2001). The measured band-splits are consistent with moderate shock strengths, i.e. compression factors of $X \leq 2$ . However, this rests on the assumption that band-split is caused by emission coming from ahead and behind of the shock (Smerd et al. 1975). We cannot deduce X if band-split is due to some other cause, such as the orientation of the shock and its curvature (Holman & Pesses 1983).

The shock area $A_{\rm s}$ can be constrained by NRH radioheliograms. As an example, Fig. 2 shows the TS source in the flare of 2001 Mar. 29 imaged at 327 and 237 MHz overplotted on a SOHO/EIT image (Delaboudinière et al. 1995) showing the flaring AR. Note that the source at 237 MHz has moved by only 30 Mm with respect to the source at 327 MHz, although it was imaged more than 3 min later. This proves the stationary nature of the TS source.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig2.eps}\end{figure}$	Figure 2: Radio source of the TS in the X1.7 flare of 2001 Mar. 29 imaged by NRH. The background image shows the flaring active region in EUV (SOHO/EIT) at 10:13:20 UT. The white contours show the TS source at 327 MHz and 10:05:24 UT, while the dashed black contours show the TS at 237 MHz and 10:08:44 UT. The white ellipse in the upper left corner shows the NRH beam at 327 MHz.
Open with DEXTER

Taking the 50% contour of the NRH source at 327 MHz (the outermost white contour of the TS source in Fig. 2), we obtain a shock are of $A_{\rm s}=1.3 \times 10^{20}$ cm². Using this method, areas in the range of $A_{\rm s}=1$ - $3\times 10^{20}$ cm² are found for the different TS events. Note that these areas are very large and more comparable to active region sizes than to the areas of HXR sources. Are they realistic? One issue is instrumental resolution - at 327 MHz, the beam size of NRH is $\approx$ 60'' in the east-west direction, and about twice as much in the north-south direction (see Fig. 2). However, this is significantly less than the half-power widths of the TS sources, which range from 150'' to 270''. The second effect that has to be considered is the scattering of radio waves in the corona which leads to an increase of the apparent size of the source. The smallest sources detected at 327 MHz have half-widths of a few 10'' (e.g. Mercier et al. 2006, and references therein). We conclude that while our measured source sizes are certainly affected by resolution issues and scattering, it is unlikely that the true source areas will be significantly less than 10²⁰ cm². For a temporally and spatially fragmented TS, the effective shock area would probably be lower than the observed one. However, such an event would not be identified as a TS because of the lack of the characteristic spectral signature. Thus, the ``filling factor'' in the clear events we have observed is probably close to unity.

Thus far we have assumed that the TS signatures we have observed around 300 MHz are due to the lower TS. However, this identification is only unambiguous for the event of 2003 Oct. 28 (Aurass & Mann 2004), where both lower and upper TS signatures were observed. By inference, one could claim that the signatures around 300 MHz in the other events are also due to the lower TS, but this cannot be proven conclusively.

2.2 Constraints on the TS from other observations

Note that the TS radio sources are quite large and appear at quite high altitudes (of the order of 100 Mm) over the flaring AR. In contrast, there are inferences from time-of-flight studies that the acceleration height of electrons is of the order of a few 10 Mm (e.g. Aschwanden et al. 1996). This is supported by RHESSI imaging observations which suggest that the reconnection site is located at heights of 10 to 40 Mm (Sui & Holman 2003; Sui et al. 2004), as well as by the detection of hot plasmas above the flaring loops by Yohkoh (e.g. Tsuneta et al. 1997; Nitta et al. 2001) and TRACE (e.g. Warren & Reeves 2001). The sizes of these sources are typically a few tens Mm.

Judging from these observations, one would expect the lower TS to be of smaller extent and at lower heights than we have derived from radio observations. This inconsistency between SXR/HXR and radio observations may be explained by interpreting the TS signatures around 300 MHz as being generated by the upper TS. The lower TS would then be located at heights of a few 10 Mm, corresponding to plasma frequencies of $\geq$ 1 GHz. At these heights, plasma radiation suffers strong free-free absorption, thus the lower TS signature would probably be not observable.

The discrepancies between radio-derived and EUV/ SXR/HXR-derived shock sizes and heights will require further investigation. However, two points should be noted here: firstly, only the radio features are an unmistakable shock signature, while EUV/SXR/HXR observations merely show the presence of hot plasma. Secondly, the smaller length scales derived from the HXR observations refer to the impulsive phase. Since the reconnection site rises as the flare progresses, the apparent discrepancy in scales may not exist during the gradual phase, and the radio signatures that are observed late in the events may well be due to the lower TS after all.

Interestingly, a large-area/low-density shock and outflow jet as suggested by the radio observations would be very difficult to detect in other wavelength ranges. Assuming, for the peak of the impulsive phase of a large flare, a shock area of $A_{\rm s}=1 \times 10^{20}$ cm², a distance between shock and reconnection region of 200 Mm, and a uniform outflow density of $N_0=1 \times 10^9$ cm^-3, we obtain an emission measure of $EM=1 \times 10^{48}$ cm^-3 for the outflow (this is almost certainly an overestimation, since densities will be closer to $1 \times 10^{8}$ cm^-3 at the greater heights). Comparable values are derived for the downstream (shocked) plasma. At the same time, the evaporated plasma filling the flaring loops has an EM of typically several times 10⁴⁹ cm^-3 (e.g. Holman et al. 2003). Even if the outflow and/or the shocked plasma are hotter than the material in the flare loops, these components will not be detected in HXR spectra because the evaporated plasma dominates up to several tens of keV, where any high-temperature component will be swamped by the nonthermal radiation. The same applies to GOES SXR measurements, and indeed any EUV or X-ray spectral observations. Similarly, HXR imaging by RHESSI will not detect an extended source of low surface brightness when flaring loops are present. Events where the flare loops are occulted by the solar limb may offer the only opportunity to detect the thermal emission of an extended TS.

2.3 Constraints on electron acceleration from HXR observations

In order to evaluate possible electron acceleration mechanisms, we must first determine the characteristics of the injected electrons, i.e. the electron flux spectrum. The recent years have seen tremendous advances in this field due to the launch of the RHESSI spacecraft, a HXR and $\gamma$ -ray spectroscopic imager (Lin et al. 2002). The high spectral resolution of RHESSI for the first time allows a clear separation between thermal and nonthermal HXR spectral components which is mandatory for obtaining accurate values for both thermal energy content and nonthermal electron flux.

The injected nonthermal electron flux spectrum, F(E) (in electrons s^-1 keV^-1), can be derived from RHESSI spectra by using a forward-fitting method (see Holman et al. 2003, and references therein) under the assumptions that the nonthermal HXR emission is thick-target bremsstrahlung (Brown 1971) and that F(E) is a broken power-law. As an example, Fig. 3 shows a spectrum from the impulsive phase of the well-studied X4.8 flare of 2002 Jul. 23. In this example, a total nonthermal electron flux of $F_{\rm tot}=\int{F(E) dE}=2.1 \times 10^{36}$ s^-1 is obtained.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig3.eps}\end{figure}$

Figure 3:

RHESSI HXR photon spectrum for the X4.8 flare of 2002 Jul. 23, integrated over the period of 00:26:40-00:27:00 UT. The background-subtracted photon flux (plus signs; the background is shown by the horizontal bars) is plotted as a function of photon energy in units of keV and is fitted with a thermal bremsstrahlung contribution from an isothermal plasma (dotted curve) and a double power-law nonthermal electron flux component with a low-energy cutoff (dashed line). The best-fit parameters are shown in the plot.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig4.eps}\end{figure}$

Figure 4:

RHESSI HXR light curves and time series of fit parameters for the X4.8 flare of 2002 Jul. 23. Shown are count rates in three energy bands, spectral indices (crosses denote $\delta _{\rm L}$ and diamonds refer to $\delta _{\rm H}$ ), break energy, low-energy cutoff, total flux and total kinetic power (both integrated over all energies above the low-energy cutoff) of the injected nonthermal electrons.

Open with DEXTER

We can now do this spectral fitting for a whole series of spectra, thus obtaining the temporal variation of the electron parameters over a whole flare. As an example, Fig. 4 shows the fitting results for the flare of 2002 Jul. 23. Apart from the HXR lightcurves of the event, the plot shows the power-law index of the injected electron flux below and above the spectral break, $\delta _{\rm L}$ and $\delta _{\rm H}$ , the break energy $E_{\rm B}$ , the low energy cutoff $E_{\rm L}$ , and the total flux $F_{\rm tot}$ and total kinetic power $P_{\rm tot}$ of the injected nonthermal electrons. For this flare, the same kind of analysis has been done by Holman et al. (2003) and Emslie et al. (2005), and we obtain comparable results. Note that the maximum values of $F_{\rm tot}$ and $P_{\rm tot}$ in Fig. 4 are comparable to what was found for the X17.2 flare of 2003 Oct. 28, where we found the excellent temporal correlation between TS signature and HXR and $\gamma$ -ray emission (see Paper I). It should be kept in mind that $F_{\rm tot}$ and $P_{\rm tot}$ are often only lower limits because the true low-energy cutoff is masked by the thermal emission.

In order to obtain a representative range of spectral parameters that our model must reproduce, we have made spectral fits (with 4 and 20 s integration times) as a function of time for 18 flares, ranging in importance from C5.5 to X17.2 (a detailed analysis of this sample is currently under preparation). In total 1053 spectra with a nonthermal component were fitted. Figure 5 shows $P_{\rm tot}$ versus $F_{\rm tot}$ for all spectra - it is evident that an electron flux of the order of $F_{\rm tot}=10^{36}$ s^-1 and a total kinetic power of $P_{\rm tot}=10^{29}$ erg s^-1 represent reasonable peak values in large flares (extremely large flares may peak at a few times these values). Thus this is the most fundamental constraint that any acceleration mechanism has to fulfill. Further constraints include the spectral shape of the electron flux as well as its evolution in time.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig5.eps}\end{figure}$	Figure 5: Total kinetic power $P_{\rm tot}$ versus total flux $F_{\rm tot}$ of the injected nonthermal electrons as obtained from thick-target fits of 1053 RHESSI spectra observed in 18 solar flares.
Open with DEXTER

3 Modeling

A fully relativistic theory of shock drift acceleration of electrons has been developed in Paper I. Here, we use this mechanism to model SDA at the TS. The TS is a fast magnetosonic shock wave, which is accompanied by a jump of the magnetic field strength across the shock (``switch-on shock''). That jump is connected with an electric field, and consequently with a current in the shock transition region. According to SDA, the inflowing charged particles are reflected at the shock since the sharp increase the field strength is acting as a moving magnetic mirror (moving with respect to the outflow). During the reflection, the particles are accelerated by the electric field localized within the shock transition region. As a result, the combined action of the magnetic and electric field at the shock leads finally to an energy gain of the particles. Thus, the movement of the particles along the electric field within the shock transition region contributes to the current flowing within this region. Note that while SDA is also capable of accelerating protons and heavier ions, we only consider electron acceleration in this work.

The principal input parameters of our SDA model are the temperature T in the outflow jet upstream of the shock, the compression factor X at the shock, the shock speed $v_{\rm s}$ and the angle $\theta$ between the shock normal and the upstream magnetic field. These parameters are sufficient to calculate an electron flux density spectrum normalized by the electron density. A multiplication with the upstream electron density N₀ and the shock area $A_{\rm s}$ then yields the actual electron flux spectrum F(E) (in electrons s^-1 keV^-1).

In Paper I, we have developed the SDA mechanism for an initial Maxwellian distribution function as well as for a Kappa distribution function (e.g. Maksimovic et al. 1997). In the present work, we will primarily be concerned with the Maxwellian case, while aspects of an initial Kappa distribution will be discussed in Sect. 4.3.

3.1 Geometric model

Applying our SDA mechanism to modeling acceleration in a solar flare requires several modifications. Firstly, acceleration in a real flare will not be characterized by a single value of the angle $\theta$ , since the relaxing field lines which are moving with the outflow will have some curvature. This is sketched in Fig. 6. Thus, there will be a whole distribution of angles over the shock surface, starting at some minimum angle $\theta_{\min}$ at the outer edges of the shock. We therefore calculate 100 individual spectra for equally spaced points at the shock between its outer edge ( $\theta=\theta_{\min}$ ) and a point near its center where a maximum angle $\theta_{\max}$ is reached, and take the average of these spectra. The individual values for $\theta$ are given by assuming circular or parabolic curvature of the field lines. We found that both scenarios give very similar results, thus all results shown in this paper will be derived using circularly curved field lines. Details can be found in Paper I. Since the SDA mechanism yields the electron flux parallel to the field lines, $j_{{\rm acc},\parallel}(E)$ (see Paper I), we have to consider a geometric factor of $\cos \theta$ when calculating the contribution of each shock unit area.

$\begin{figure} \par\includegraphics[width=4cm,clip]{fig6.eps}\end{figure}$	Figure 6: Geometry of SDA at the TS. Magnetic field lines are reconnected in the diffusion region (DR) and two outflow jets are formed. The inflow is separated from the outflow by two pairs of slow-mode standing shocks (SMS). In the reconnection outflow jets fast-mode termination shocks (TS) have formed (only the lower one is shown). For details see main text.
Open with DEXTER

The maximum angle is reached at the point where the projected shock speed along the field line reaches the speed of light, i.e. $v_{\rm s} / \cos \theta_{\max}=c$ . Beyond this point, our SDA mechanism is no longer valid. This implies that only a certain fraction of the shock area is actually contributing to the electron fluxes we calculate.

3.2 Input parameters

The second modification concerns the input parameters. For the parametric study, we want to study the effects of the variation of independent input parameters. However, $v_{\rm s}$ is coupled to N₀, X and T by the Rankine-Hugoniot equations (see e.g. Priest 1982). We therefore choose N₀ as an independent variable and calculate $v_{\rm s}$ from the other variables. From N₀ we can derive the height h of the shock. Since we want to reproduce also large events which are typically associated with big and strong active regions, we use a version of the density model developed by Warmuth & Mann (2005). This model represents both the active region and the quiet corona and provides for a smooth transition between both. The parameters are chosen in such a way that the density at the coronal base is equivalent to eight times the density given by the Newkirk (1961) model ( $N_0=6.1 \times 10^9$ cm^-3), while at 1.3 Rs the density of the single Newkirk model ( $N_0=8.7 \times 10^7$ cm^-3) is reached. We then take twice this model to reflect the density enhancement of the outflow jet.

From h we then obtain the upstream magnetic field strength B₀ using the model of Dulk & McLean (1978). Note that this is a rough approximation, since this model reflects a typical active region, and not an outflow jet in a large flare. To study the effect of different magnetic field strengths, we will also vary B₀. We can now calculate the Alfvén speed $v_{\rm A}$ . Combined with the temperature, the plasma beta upstream of the shock is $\beta_{\rm p} = 8 N_0 k_{\rm B} T / B_0^2$ , with $k_{\rm B}$ as Boltzmann's constant. In the quasi-perpendicular approximation, the Alfvénic Mach number is then $M_{\rm A}=\sqrt{(5 \beta_{\rm p} +5+X)X/(8-2 X)}$ (e.g. Priest 1982), and we obtain the shock speed $v_{\rm s}=M_{\rm A} v_{\rm A}$ . Note that $v_{\rm s}$ increases with increasing X, T, and N₀.

Finally we have arrived at the independent input parameters N₀, X, T and $\theta_{\min}$ ( $\theta_{\max}$ is calculated from $v_{\rm s}$ ). The output of the model is now the electron flux spectrum per unit shock area, j(E). This is the flux density averaged over the total shock area, including the part where there is no contribution from SDA. $A_{\rm s}$ remains as the sole multiplicative factor, giving the injected electron flux spectrum via $F(E)=j(E) A_{\rm s}$ .

3.3 Parametric study and input parameter ranges

$\begin{figure} \par\includegraphics[width=8cm,clip]{101fig7.eps}\hspace*{7mm} \includegraphics[width=8cm,clip]{101fig8.eps}\end{figure}$

Figure 7:

Left: integrated nonthermal electron flux density $j_{\rm tot}$ (top) and kinetic power density $P_{\rm tot}/A_{\rm s}$ (bottom) as a function of $\theta_{\min}$ . Right: corresponding acceleration efficiency (top), defined as the ratio of $j_{\rm tot}$ to the total incoming flux density, and shock fraction (bottom), which is the fraction of the shock area where SDA is valid. Crosses represent $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ and acceleration efficiency integrated over all energies, diamonds, triangles and squares represent these quantities above a low-energy cutoff of 10, 20, and 30 keV, respectively.

Open with DEXTER

The parametric study of our model involves a variation of each input parameter. While each parameter is varied, the others are left constant. The variation yields information on how the input parameters affect the resulting electron flux spectra, and on whether the electron fluxes derived from HXR observations can be reproduced. Thus, choosing realistic input parameter ranges is essential if we want to find out if the proposed acceleration model is able to reproduce the observations. We will now discuss the parameter ranges used for the four input parameters, as well as try to determine the most realistic values that are chosen as the ``default'' values (these are the values used for the input parameters which are left constant in each parametric run):

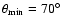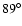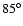the minimum shock angle $\theta_{\min}$ is probably the least well-constrained parameter, thus we include a wide range in the quasi-perpendicular regime, namely $\theta_{\min}=70^\circ$ - $89^\circ$ . As default value, we take $85^\circ$ (cf. the discussion in Paper I).
for the compression factor X practically the whole theoretically possible range is used, namely from 1.1 to 3.9. A default of X=2 is chosen according to the discussion in Sect. 2.1;
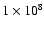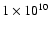N₀ is varied from $1 \times 10^{8}$ cm^-3 to $1 \times 10^{10}$ cm^-3. This range covers the densities derived from the TS radio signatures under the assumption that they are due to the lower TS, as well as the higher densities associated with shocks at very low heights that cannot be observed in radio (see the discussion in Sect. 2.1). In our model, the maximum value of N₀=10¹⁰ cm^-3 corresponds to a minimum height of the shock of h=20 Mm, which is consistent with the acceleration heights found by Aschwanden et al. (1996) and with RHESSI observations of coronal sources (e.g. Sui et al. 2004). 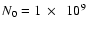A mean value of $N_0=1~\times~~10^9$ cm^-3 is taken as default;
there is not much information on the temperature of the outflow jets, however, there are different observations which point to the presence of high-temperature plasmas above the flaring loops, which is just where an outflow jet or its termination is expected. From Yohkoh observations, temperatures of 20-30 MK have been derived for these plasmas (e.g. Nitta et al. 2001), while Tsuneta et al. (1997; see also Masuda et al. 2000) have even reported temperatures as high as 100 MK. EUV observations have shown emission of the Fe XXIV line in cusps above flaring loops (e.g. Warren & Reeves 2001), suggesting temperatures of over 20 MK. The flaring loops themselves contain plasma up to 40 MK. Magnetic reconnection models predict that the outflow will be heated by the slow-mode shocks to temperatures between 5 and 80 MK, depending on 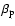$\beta_{\rm p}$ (Vrsnak & Skender 2005). We use the same range for our parametric study, choosing a mean value of T=40 MK as default.

The upstream magnetic field strength is not an independent input parameter but results from our model, however, since it is not well constrained, we also vary B₀ in order to study its influence. For this run, the value of B₀ given is multiplied by a factor ranging from 0.1 to 10. The default input parameters give B₀=6.9 G.

Finally, we have to consider whether the shock speeds that are calculated from our input parameters are realistic. For our default model, we find $v_{\rm s}=1~852$ km s^-1, and the total range of $v_{\rm s}$ from our parametric study is 1000-8000 km s^-1, with the values greater than 4000 km s^-1 corresponding to strong compression (X > 3). Wang et al. (2007) have presented SOHO/SUMER observations showing fast coronal up- and downflows in a solar flares. Accounting for projection effects, outflow jet speeds between 900 and 3500 km s^-1 were derived. This is in agreement with the speed range given by the parametric study as long as we do not go to greater values for compression.

4 Discussion

4.1 Total flux, kinetic power, and acceleration efficiency

The most basic observational constraints on electron acceleration are the total electron injection rate $F_{\rm tot}$ and the corresponding kinetic electron power $P_{\rm tot}$ . We now study how a variation of the different input parameters affects these quantities, and if the values derived from RHESSI observations can be reproduced by the model.

Figure 7 (left) shows the accelerated electron flux densities per unit shock area, $j_{\rm tot}$ (top) and kinetic power densities $P_{\rm0tot}/A_{\rm s}$ (bottom) as a function of $\theta_{\min}$ (the other ``default'' parameters are given at the top of the plot). $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ are shown integrated over all energies (crosses), and above low-energy cutoffs of 10 keV (diamonds), 20 keV (triangles), and 30 keV (squares). According to HXR observations (cf. Fig. 5), the latter two values seem to be reasonable for the low-energy cutoff in large flares, so the following discussion will be focused on these fluxes. The total accelerated flux and power can be easily obtained by multiplying $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ by the shock area.

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig9.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig10.eps} } \end{figure}$	Figure 8: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of X.
Open with DEXTER

As $\theta_{\min}$ is increased, flux and power slowly rise, reach a maximum around $\theta_{\min}=87^{\circ}$ and then drop off rapidly. We note that flux and power vary only by a factor of $\approx$ 2 with $\theta_{\min}$ below the maximum. Thus our lack of information on $\theta_{\min}$ will not significantly affect the results, as long as the minimum angle remains below $\approx$ 88 $^{\circ}$ . Note also that as $\theta_{\min}$ is increased, the different flux curves move closer together. This means that more and more electrons are accelerated to higher energies - at $88^{\circ}$ , all curves have converged, meaning that all accelerated electrons have energies above 30 keV.

$\begin{figure} \par\mbox{\includegraphics[width=8cm]{101fig11.eps}\hspace{1cm} \includegraphics[width=8cm]{101fig12.eps} } \end{figure}$	Figure 9: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of N₀.
Open with DEXTER

The right side of Fig. 7 shows the acceleration efficiency (top) and shock fraction (bottom). The former is defined as the ratio of the accelerated flux density to the total incoming flux density, while the latter is the fraction of the shock where SDA is valid (see Sect. 3.1). Here, the flux density is averaged only over the contributing part of the shock, and the incoming flux density is given by $N_0 v_{\rm s}$ . As for $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ , we plot the efficiency integrated over all energies as well as above cutoff energies of 10, 20 and 30 keV. As $\theta_{\min}$ is increased, less electrons are accelerated, and the total efficiency drops. Initially, the efficiency actually rises for energies >20 keV, because the energy gain per electron rises with increasing $\theta$ . For $\theta_{\min}>88^{\circ}$ , this effect can no longer compensate the fact that less electrons are accelerated in total, and the efficiency begins to drop also at higher energies. Concurrently, the shock fraction shrinks rapidly.

Figure 8 shows the dependence of $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ on the compression ratio X. Again, increasing X leads to higher fluxes and power, until a maximum is reached around X=3 beyond which the flux decreases. Note that an increase of X has a much stronger effect on the flux than an increase of $\theta_{\min}$ : the fluxes increase by two orders of magnitude from X=1.1 to X=3. As for $\theta_{\min}$ , increasing X leads to more electrons gaining higher energies, and at X=3.5 nearly all accelerated electrons have energies above 30 keV. The acceleration efficiency shows the same trend as the fluxes. How can we interpret this behavior? In SDA, the accelerated flux is a monotonously increasing function of X, meaning that it increases all the way to X=4. In our model, however, X is coupled to the shock speed $v_{\rm s}$ over $M_{\rm A}$ , and increasing X also increases $v_{\rm s}$ . As with $\theta$ , higher shock speeds lead to greater energy gains, but a lower total number of accelerated electrons. When this regime is entered at around X=3 (corresponding to $v_{\rm s}=3500$ km s^-1), the total efficiency begins to drop.

The variation of $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ as a function of the upstream electron density N₀ is shown in Fig. 9. Since N₀ represents the initial reservoir of electrons that can be accelerated, the flux increases nearly linearly with N₀. Also, acceleration efficiency and shock fraction stay constant until densities above $N_0=5 \times 10^9$ cm^-3 are reached. At the corresponding low heights, B₀ increases strongly, implying also high $v_{\rm s}$ . This is the cause of the decreasing efficiency and also of the drop in shock fraction.

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig13.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig14.eps} } \end{figure}$	Figure 10: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of T.
Open with DEXTER

Finally, Fig. 10 shows the dependence of $j_{\rm tot}$ and $P_{\rm tot}/A_{\rm s}$ on the temperature T. It is evident that the flux increases dramatically with rising temperature, with a flux increase by almost five orders of magnitude over the range considered. The increase of flux is very rapid at the lower temperatures, say between 5 and 20 MK, and then starts to level off. Flux and power are therefore most sensitive to T. The temperatures is also the only parameter whose increase yields steadily rising acceleration efficiency. As with $\theta_{\min}$ and X, increasing T leads to higher fluxes at higher energies.

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig15.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig16.eps} } \end{figure}$	Figure 11: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of B₀.
Open with DEXTER

The upstream magnetic field strength B₀ is not an independent input parameter, but since it is not well constrained, Fig. 11 shows its influence on the accelerated flux (note that B₀=6.9 G is given by the default parameters). At first the fluxes increase until field strengths of about 15-35 G are reached (higher energy fluxes peak at higher field strengths), then they decrease. The total variation is not very high - 1-2 orders of magnitude, depending on whether flux or power are considered, and at which energies. We note that the fluxes peak at $\approx$ 3-5 times the default field strength. These maximum fluxes are only slightly larger than the ones derived from our model B₀-1.5 times for E>20 keV and 3 times for E>30 keV. Decreasing B₀ has even less effect: a field strength of a tenth of our model value reduces flux and power by less than 20%. Therefore, we do not have to worry about the effect of an inaccurate B₀ - as long as the field strength is not too high, the effect on the fluxes is negligible compared to the influence of the input parameters.

Much higher values of B₀ are not to be expected, since B₀ is the field strength in the outflow, which will necessarily be lower than the ambient magnetic field strength (see Sect. 4.2). Recently Aurass et al. (2005) have developed a method of measuring the magnetic field strength in flaring loops by means of fiber burst observations. Rausche et al. (2007) and Vocks et al. (2008) have applied this method to the 2003 Oct. 28 event, showing that even in large and strong flares/ARs the field strength in the flaring loops is not significantly above the values given by Dulk & McLean (1978). Moreover, considering that the TS is characterized by a magnetic field compression, these measurements reflect the field strengths downstream of the shock, while the upstream B₀ is lower by a factor of X. Shocks at low heights are associated with higher field strengths, but this countered by the effect that a shock at higher densities can accelerate efficiently for higher field strengths - while for N₀=10⁹ cm^-3, $B_0 \approx 30$ G is optimum, while at N₀=10¹⁰ cm^-3, peak efficiency is reached around 100 G.

In order to compare the calculated flux densities with the results obtained from HXR observations, we have to multiply $j_{\rm tot}$ with the shock area $A_{\rm s}$ . Let us now consider some numerical examples. For large flares, $F_{\rm tot}=10^{36}$ s^-1 and $P_{\rm tot}=10^{29}$ erg s^-1 are required (see Sect. 2.3). Taking a moderate temperature of T=10 MK (and again taking our default values for the other parameters), this would require a shock with $A_{\rm s}=1 \times 10^{22}$ cm², which corresponds to a circular area with a diameter of d=1 140 Mm. It is immediately evident that such a large-scale stationary shock - nearly as big as the sun itself - cannot exist in the solar corona. If we take a higher (but still realistic) temperature T=40 MK, a shock area of $A_{\rm s}=6 \times 10^{19}$ cm² is needed. This is still rather large (corresponding to a circle with d=87 Mm), but it is on the same order of magnitude as an AR. Since large flares are typically associated with big and complex ARs, such shock areas may well be realized, and indeed they are consistent with the TS source areas determined from NRH radioheliograms (see Sect. 2.1). If we assume a shock at low heights, i.e. corresponding to N₀=10¹⁰ cm^-3, $A_{\rm s}=5 \times 10^{18}$ cm² is sufficient. This is comparable to the size of coronal thermal sources and above-looptop sources in large flares.

We have performed our parametric study with a default temperature of T=40 MK, however, the required fluxes can also be produced by the same shock area and upstream density with lower temperatures, provided that the compression is increased accordingly. For example, a model with T=20 MK requires X=2.9 to produce the same flux as the default case.

From our parametric study, we have seen that the required nonthermal electron fluxes can indeed by reproduced by SDA at the TS, provided that some conditions are fulfilled. Most importantly, there has to be strong heating of the outflow at the slow-mode shocks, and the shock area has to be large enough. We stress that a quantitative agreement between modeled and observed fluxes has been achieved even for the most demanding case (as shown in Paper I) - the event of 2003 Oct. 28 was one of the largest flares ever observed, while at the same time the associated TS was found at low densities of $N_0 \approx 3 \times 10^8$ cm^-3 (this was the only TS event where we could accurately determine N₀). This close agreement between theory and observations shows that our model is able to reproduce the required fluxes also for individual events, even though we have always used conservative values for the model input parameters.

4.2 Total accelerated electron number and kinetic energy

We have shown that the model is able to reproduce the peak electron fluxes and kinetic powers even in large solar flares. This implies that the time-integrated total number of accelerated electrons and the associated total kinetic energy can be obtained quite easily, since the TS is continuously supplied with electrons from the outflow jet. With respect to these totals, another issue is more important: are there enough electrons and enough magnetic energy available to power the flare?

Let us consider once more our scenario. A fraction of the electrons from the outflow jet is accelerated at the shock and transmitted downstream. The nonthermal electrons then propagate to the chromosphere where they are thermalized. As long as reconnection is going on, the outflow jet will continue to supply fresh electrons to the shock which can then be accelerated. As a plasma volume element passes through the shock, the acceleration will create a charge imbalance. This imbalance in the downstream region will generate electric fields that drive return currents which finally reestablish charge neutrality. No charge imbalance develops in the upstream region, which is continually replenished by the neutral outflow. This also means that the return current does not have to reach the upstream region.

With regard to charge neutrality, return currents are thus not required to cross to the upstream region. However, what such a replenishment from below could achieve is a reduction of the number of electrons that have to be supplied from the ambient corona. However, it is beyond the scope of this work to study if a return current - or also evaporated plasma - could cross to the upstream region, so we retain the more conservative scenario of the electrons coming only from the outflow, without any electron reprocessing going on.

Our RHESSI spectroscopy has shown that in large flares up to several 10³⁸ electrons are accelerated, carrying a total kinetic energy of a few 10³¹ erg. These values are compatible with the results of Emslie et al. (2005). With a typical acceleration fraction of 10% (see Figs. 7 to 11), this means that several 10³⁹ ambient electrons are required. Assuming a mean coronal density of 10⁹ cm^-3, this electron number is contained in a volume of several 10³⁰ cm³. Such a volume is given by the third power of the linear dimensions of the radio TS signatures (i.e. a box with an edge length of $\approx$ 100 Mm), and is consistent with the extent of a big AR.

The second important issue is total energy. It is well accepted that the energy driving solar flares is originally stored in coronal magnetic fields. Via reconnection - and the corresponding annihilation of magnetic fields - the stored energy is converted to other forms of energy, primarily into kinetic energy of the outflow jet. Quite similar to the acceleration efficiency, the energy conversion efficiency (defined as the kinetic energy of nonthermal electrons divided by the total outflow kinetic energy) is typically of the order of 10%, so a total of a few 10³² erg have to be converted from the magnetic energy. Taking the same volume as above, this corresponds to a field strength of $\approx$ 50 G. Since of course not all of the field will be converted, the mean ambient field required will be higher than that. Vrsnak & Skender (2005) have calculated that the ratio of the magnetic field strength upstream and downstream of the slow-mode shocks is typically greater than 5, corresponding to $\geq$ 80% of the field being dissipated. This implies that the average ambient field strength does not have to be significantly higher than 60 G, which should be fulfilled in a big and strong AR. Accordingly, the field strength in the outflow can be low enough to allow efficient acceleration (cf. Sect. 4.1).

4.3 Spectral shape

Apart from the total fluxes of the nonthermal electrons, also their characteristic spectral shape has to be reproduced. Most nonthermal HXR spectra are consistent with single or double power-law injected electron spectra, with spectral slopes $\delta$ in the range of $\approx$ 2-10 (cf. Figs. 4 and 14). In double power law spectra, the spectral index above the break energy is usually larger than the one below the break by $\approx$ 2. (cf. Fig. 4), so the spectra soften at higher energies. The break energy is located between a few ten and a few hundred keV. In large flares, there seems to exist a second electron component above $\approx$ 500 keV which extends beyond 10 MeV and is harder than the component at lower energies (e.g. Lin et al. 2003).

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig17.eps}\end{figure}$	Figure 12: Top: injected electron flux density spectrum j(E) as given by the shock-drift acceleration model using the default values for the input parameters (given in the figure). Bottom: corresponding spectral index $\delta (E)$ as a function of energy. The dotted curves in both plots show j(E) and $\delta (E)$ of the initial Maxwellian distribution for comparison.
Open with DEXTER

Figure 12 (top) shows the injected electron flux density spectrum, j(E), computed with the default values of the model input parameters. Starting from the low-energy cutoff at 2 keV ( $E_{\rm LC}$ ), j increases slightly up to 10 keV. Beyond this maximum ( $E_{\max}$ ), j decreases, slowly at first, but increasingly fast at higher energies, say above 100 keV. This is also reflected by the energy-dependent spectral index, $\delta (E)$ , shown in the lower part of Fig. 12. It is evident that the computed spectrum is not a power law: in such a case, $\delta (E)$ would be constant, while in the broken power-law, there would be two values for $\delta$ with a sharp transition at $E_{\rm B}$ . While the exact location of the low-energy cutoff and the maximum of the flux as well as $\delta (E)$ are of course dependent on the input parameters, these general characteristics are found for all spectra.

Traditionally, nonthermal photon spectra are modeled with simple or broken power laws, giving the photon spectral index $\gamma$ , which is related to the electron spectral index by $\gamma \approx \delta$ -1. However, the application of an inversion technique based on regularization - which does not assume a power-law in the first place - has shown that there are no truly sharp transitions in $\gamma(E)$ , but rather a smoother increase of $\gamma(E)$ at rising energies (Kontar & MacKinnon 2005). The same technique can be applied to the electrons, and first results show that no sharp spectral breaks are found there, either (Kontar et al. 2005). This is consistent with our modeled spectra, and in the range of 10 to 100 keV, the observed spectra are quite well reproduced. However, our synthetic spectra tend to soften more strongly with increasing energy, especially beyond $\approx$ 100 keV. At this energy, we find $\delta \approx 7$ , while Kontar et al. (2005) obtain values of $\delta \approx 2$ -4. Moreover, the computed spectra soften progressively, which means that significant fluxes of 10 MeV electrons, as they are found in large flares, cannot be reproduced, even for extreme values of the input parameters.

This failure at high energies could imply that our model is plainly wrong, or that high-energy electrons belong to a separate population that is accelerated by a different mechanism. There is a third possibility, however - in fact there are at least two effects that will increase the flux at higher energies we have not yet considered:

multiple mirroring: at the reflection of electrons at the shock, their pitch angle is decreased (see Paper I), so that most of the electrons are transmitted through the shock at the second encounter. However, a small percentage of electrons is reflected a second time, gaining even more energy in the process. This would lead to a hardening of the higher-energy part of j(E). A variation of this scenario would be multiple fast-mode shocks that have formed in the outflow jet which lead to multiple shock encounters of the electrons. Such shocks were found in an MHD simulation by Tanuma & Shibata (2005);
nonthermal initial electron distribution and preacceleration: the second possibility to increase the flux at high energies concerns the initial reservoir of electrons. We have seen how important the heating of the original electron population is. In addition to being heated, electrons could also be accelerated to nonthermal energies before they reach the TS. This can happen at the slow-mode shocks, the site of strong electric currents (e.g. Sato & Hayashi 1979) or in the outflow jet, where turbulence may drive stochastic acceleration (Miller et al. 1997; Selkowitz & Blackman 2007). A further possibility is that already the ambient electrons are not conforming to a Maxwellian distribution function, but show some nonthermal tails. There are indications that Kappa distributions are consistent with the coronal plasma (see e.g. Maksimovic et al. 1997). 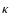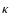In a Kappa distribution, the index $\kappa$ determines the degree of nonthermality: the higher $\kappa$ , the closer is the agreement with a Maxwellian distribution. 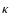Thus, $\kappa$ will not be too small in the quiet corona - 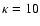$\kappa =10$ is the minimum which is still consistent with microwave observations (Holman, private comm.). In Paper I, we have also developed SDA for an initial Kappa distribution, and Fig. 13 shows j(E) computed for a Kappa distribution with 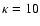$\kappa =10$ (the other parameters have the default values). The spectrum is quite similar to the Maxwellian case (cf. Fig. 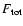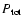12), and indeed $F_{\rm tot}$ and $P_{\rm tot}$ are almost the same. However, we see that 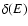$\delta (E)$ is increasing more slowly than for the initial Maxwellian distribution, especially above 100 keV, where 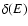$\delta (E)$ begins to increase much faster in the thermal case.
We can lower 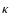$\kappa$ even more if we assume that preacceleration creates electrons with a Kappa distribution. One constraint on such a preacceleration mechanism is that it has to produce nonthermal electrons with an isotropic pitch angle distribution. With 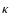$\kappa$ as low as 2, even hard spectra in large flares can be reproduced up to energies of several MeV. 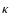However, in such a case preacceleration is actually the main acceleration mechanism: Figure 13 already shows that the increase of the flux with respect to the initial distribution is lower for the case of the Kappa distribution, and the relative increase becomes lower for smaller $\kappa$ .

In conclusion, our present SDA model is able to reproduce the observed spectra up to energies of $\approx$ 100 keV. Above that, the spectra soften too rapidly. There are several different effects that we have not yet considered which could harden the spectra at higher energies. We will address this issue in a quantitative manner in a future publication.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig18.eps}\end{figure}$	Figure 13: As in Fig. 12, but showing j(E) and $\delta (E)$ resulting from SDA acceleration acting on an initial Kappa distribution with $\kappa =10$ (dotted curves).
Open with DEXTER

4.4 Relation between flux and spectral index

We have shown that our model can reproduce the observed fluxes and, within certain limitations, spectral indices. However, this is not sufficient, since it is well known that there is a relation between nonthermal fluxes and spectral indices (first reported by Parks & Winckler 1969). Usually, an anticorrelation between the photon flux and photon power-law index $\gamma$ is observed. This is the so-called soft-hard-soft behavior (SHS; see Grigis & Benz 2004, and references therein). In contrast, some flares show a systematic hardening with time, the soft-hard-harder pattern (SHH; e.g. Kiplinger 1995). Such correlations were found for observed photon spectra, but of course they are also expected for the injected electron spectra.

We have extended the study of Grigis & Benz (2004) - who have used RHESSI spectra to derive a quantitative relation between photon flux and spectral index $\gamma$ in a series of moderately sized impulsive flares - by considering also the relation between injected electron flux and electron power-law index $\delta$ . For this purpose we use the spectral fits discussed in Sect. 2.3. Compared to Grigis & Benz (2004), our sample of 18 flares is more inhomogeneous, comprising both small and large flares, as well as impulsive and gradual ones. We determine $\delta$ in the range from 40 to 80 keV, because only relatively few spectra are consistent with $E_{\rm LC}>40$ keV, while the softening of the modeled spectra is not too strong at 80 keV (see Sect. 4.3). $F_{\rm tot}$ is strongly dependent on the low-energy cutoff, for which we can often only determine an upper boundary, therefore, we consider the electron flux at the fixed energy of 60 keV, F₆₀.

In Fig. 14, $\delta$ is plotted versus F₆₀ for all 1053 fitted spectra (black dots). It is evident that there is generally an anticorrelation between electron flux and spectral index which can be represented as a power-law. Using a least-squares bisector method, we find a power-law index of $\alpha_{\rm e}= 0.18 \pm 0.11$ . Grigis & Benz (2004), using the same technique, obtained a quite similar value for the photon spectra, $\alpha_{\rm ph}= 0.20 \pm 0.05$ . The main difference is the wider confidence range in the case of the electrons, which is probably due to our more inhomogeneous event sample. For example, we note a cluster of data points around $\delta=3$ which actually shows a positive correlation between flux and spectral slope. These points belong to large flares that show progressive hardening of their spectra (SHH).

We have thus verified that the characteristic relation between flux and spectral index must be reproduced by a viable acceleration mechanism. In order to determine whether our model also fulfills this constraint, we use the spectra calculated for our parametric study to obtain F₆₀ and $\delta$ averaged from 40 to 80 keV. The resulting data points for the variation of the different input parameters are plotted over the measured values in Fig. 7.

In order to compare the model results with the values derived from RHESSI spectra, we have to multiply the calculated flux densities by the shock area. Here, we have chosen $A_{\rm s}=10^{19}$ cm². Note that changing $A_{\rm s}$ has no influence on the spectral shape and thus only shifts the calculated curves towards lower or higher fluxes. This also implies that simply changing $A_{\rm s}$ during a flare will not be sufficient for obtaining the observed relation between flux and spectral index. Such a variation will only produce a horizontal line in the $\delta$ -F₆₀ diagram.

Increasing $\theta_{\min}$ (blue curve in Fig. 14) also has little effect on $\delta$ , only when $\theta_{\min}=89^\circ$ is approached, an anticorrelation with F₆₀ begins to develop. A variation of N₀ (orange curve) has even less effect on $\delta$ . Conversely, the variation of both X (green) and T (red) reproduces the observed trend very well. The various curves were derived for the same parameter ranges as defined in Sect. 3.3, with the exception of T, for which the data point for T=5 MK is omitted since it lies at flux values that are five orders of magnitude lower than the lowest measured values. This again proves that outflow jet temperatures of less than 10 MK are insufficient to provide adequate electron acceleration even for small flares.

Decreasing B₀ (magenta curve) has a negligible effect on spectral shape, however, if B₀ is increased by more than a factor of 5 (corresponding to $\approx$ 40 G), $\delta$ is strongly reduced and becomes even less than 1 for a factor greater than 8. This means that as long as the true field strength is less than five times the model value, any errors of our magnetic model will have only a small effect on the results.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig19.eps}\end{figure}$	Figure 14: Plot of electron spectral index $\delta$ versus electron flux at 60 keV, F₆₀. Black dots are values derived from 1053 fitted RHESSI spectra, while the colored symbols represent the model results for a variation of the input parameters $\theta_{\min}$ , X, N₀, and T, as well as for a variation of B₀. Arrowheads indicate the direction in which each parameter increases.
Open with DEXTER

In a real flare, the different parameters will of course not vary independently from each other, and a realistic treatment of the relation between the input parameters is well beyond the scope of this paper. However, what Fig. 14 does clearly show is that the model is at least in principle capable of reproducing the observed relation between electron flux and spectral index. The SHS behavior can be easily modeled by varying either T or X. For instance, it is intuitive to expect that towards the peak of the impulsive phase heating at the TS will reach a maximum, which will result in a decrease of $\delta$ . Reproducing the SHH characteristics requires the additional variation of $A_{\rm s}$ or N₀ to achieve lower fluxes without increasing the spectral index. For example, in the late phase of a flare the TS could move to greater heights, implying lower densities. Combined with a slight increase in compression, as may be the case in some larger flares, this will decrease the flux and the spectral index. Such a late increase of X may be present in only some large flares, which would explain the relative scarcity of SHH events.

Regarding shock area, it seems that $A_{\rm s}=10^{19}$ cm² is sufficient to cover most data points, small flares can even be reproduced with $A_{\rm s}=10^{18}$ cm². For the peaks of the strong events, $A_{\rm s}=10^{20}$ cm² is required for the default values of the input parameters.

We have also compared the RHESSI results with model runs using different default input parameters. We have used a default of $N_0=3 \times 10^{8}$ cm^-3 to represent a TS at large heights (this density was derived for the event of 2003 Oct. 28), and $N_0=1 \times 10^{10}$ cm^-3 is used to model a shock low down in the corona. In both cases, the results are qualitatively the same as described above for $N_0=1 \times 10^9$ cm^-3, only the required shock areas change. For the case of a shock in the low corona, $A_{\rm s}=10^{18}$ cm² is sufficient to reproduce most data points. These results are in agreement with what was found using $F_{\rm tot}$ and $P_{\rm tot}$ in Sect. 4.1. Another run was made for a cooler outflow jet with T=20 MK. Again, the relation between flux and index can be reproduced, and $A_{\rm s}=10^{19}$ cm² covers most data points. In contrast to the other runs, $\delta<4$ can only be reached for a nearly perpendicular shock with $\theta_{\min}>88.8^\circ$ , or alternatively for strongly enhanced B₀.

4.5 Low-energy cutoff

As has already been discussed in Sect. 4.3, the spectra increase from the low-energy cutoff ( $E_{\rm LC}$ ) to an energy where the flux reaches a maximum ( $E_{\max}$ ). Note that this is more consistent with the ``turnover'' model (which has a flat electron distribution below the cutoff) than with the sharp cutoff model that is usually used to fit the spectra. However, the two different cutoff models cannot be distinguished from RHESSI data (see Saint-Hilaire & Benz 2005). Saint-Hilaire & Benz found that the ``turnover'' model offers 20-25% more power. This is in agreement with the synthetic spectra: the flux below $E_{\max}$ is between 0.2 and 0.4 times $F_{\rm tot}$ , and the power residing in these low-energy electrons amounts to only between 0.05 and 0.3 times $P_{\rm tot}$ .

$E_{\rm LC}$ generally lies below 10 keV, but for high values of X or $\theta_{\min}$ , or for a strongly enhanced B₀, $E_{\rm LC}$ can reach several tens of keV. The same behavior is observed for $E_{\max}$ : normally between 2 and 20 keV, it rises up to $\approx$ 100 keV for high X, $\theta_{\min}$ , or B₀. How do these values compare to observations? We have already mentioned that the fitted HXR spectra usually allow only the determination of an upper limit of the low-energy cutoff, because the true cutoff is masked by thermal emission. In the majority of our fitted spectra $E_{\rm LC}$ is between 20 and 40 keV, while some spectra from the early phase of a few flares (``early impulsive flares''; see Sui et al. 2007),were consistent with values as low as $E_{\rm LC} \approx 10$ keV. At the other extreme, some spectra from the late flares of large flares can have cutoffs of up to nearly 100 keV (cf. Holman et al. 2003).

The latter values can be reproduced by using high values for X, $\theta_{\min}$ , or B₀. For all other cases, the SDA model yields cutoffs which are significantly lower than the values obtained by spectral fitting. This is consistent with masking of the cutoff by thermal emission in most spectra. For our default model, we find $E_{\max}=10$ keV, which is consistent with the minimum values found by spectral fitting.

The SDA model thus predicts that in most cases the total electron flux and power will be higher than the values derived by spectral fitting. To quantify this effect, we find that for low values of T or X, $F_{\rm tot}$ and $P_{\rm tot}$ can be up to two orders of magnitude larger than the flux and power above 20 keV. In the default parameter range, the total fluxes and powers are still higher by factors between 2 and 4. Recent observations of white light flares have shown that their luminosities are comparable to the electron beam powers only if $E_{\rm LC}$ is well below 25 keV (Fletcher et al. 2007). They find that the beam power has to be increased relative to the power above 25 keV by a factor of 4-10, which is just what the SDA model predicts for the default values of the input parameters as well as for somewhat lower T or X.

4.6 Acceleration timescales

At nonthermal energies, almost all flares show pulsed time structures on subsecond time scales. In a study of 640 BATSE flare events, Aschwanden et al. (1995) found the most typical HXR pulse durations in the range of 0.3-1 s, with a median of 0.65 s. The origin of these pulses is usually assumed to be bursty reconnection. However, there is also an implication for the acceleration mechanism itself: the acceleration timescales have to be of the same order of magnitude as the pulse durations or shorter, otherwise, the short pulses would be smeared out.

For SDA, the acceleration time of the reflected electrons can be estimated from the magnitude shock electric field, i.e. $\vec{E}_{\rm s}=\vec{v}_{\rm s}/c \times \vec{B}$ . Using our default parameters, this field is able to accelerate electrons up to 100 keV in ${\approx}10^{-6}$ s. This corresponds to a drift length along the shock surface of less than 100 m. The extremely short acceleration times due to the strong electric field at the shock mean that any fast temporal variations of the electron flux can be easily reproduced by SDA, even for GeV electrons.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig20.eps}\end{figure}$	Figure 15: Accelerated electron flux density for a single field line, $j_{\rm bin}$ , integrated over four energy bins (given in the figure) as a function of time.
Open with DEXTER

However, there is another factor in our model which influences the temporal profile of the electron flux, namely the transit of the reconnected field lines through the shock. During this transit, $\theta$ becomes progressively larger along each field line, leading to a constantly changing electron flux accelerated at each field line. When the electron flux of such an individual field line is binned to various energy intervals and plotted as a function of time, a characteristic rise and fall is observed at each energy, which is due to the changing acceleration efficiency at the different energies as $\theta$ increases. Again, this variation due to the shock transit must not be greater than the observed HXR pulse timescales, or the pulses would be smeared out. Figure 15 shows the accelerated flux density accelerated at a single fieldline, $j_{\rm bin}$ , as a function of time in different energy bins. Here, we have used the default input parameters and a shock diameter of 60 Mm, which corresponds to the footpoint separation in the large flare of 2003 Oct. 28. With increasing energy, the fluxes peak later and the pulse width decreases. The pulse width is 0.15 s (FWHM) at 25-50 keV and 0.05 s at 50-100 keV, the two energy ranges used in the study by Aschwanden et al. (1995). These values are lower than the observed pulse widths, thus the model fulfills the constraint posed by fast temporal variations.

4.7 Time lag between reconnection and acceleration

Miklenic et al. (2007) have recently compared the magnetic flux change rate $\dot \varphi$ (in other terms, the global reconnection rate) with the HXR flux as observed by RHESSI in the M 3.9 flare of 2003 Nov. 18. They found a good correlation of $\dot \varphi$ - which was determined using the chromospheric flare ribbons observed in EUV and H $\alpha$ - with the HXR flux at 20-60 keV, however, the peaks in the magnetic flux change rate occurred earlier than the associated HXR peaks by $\approx$ 1 min. Miklenic et al. speculate that this delay could be related to the travel time of the reconnected field lines from the diffusion region to the lower edge of the current sheet. In our model, this delay could represent the time the newly reconnected field lines need to reach the TS, or more precisely, to reach the quasiperpendicular regime. SDA can produce a small amount of nonthermal flux even for smaller angles $\theta_{\min}$ , and even if the newly reconnected field lines have not yet contact to the shock, energy can be put into the chromosphere by Joule heating, creating flare ribbons in EUV and H $\alpha$ . Ribbons can thus be created even before the majority of the nonthermal electrons have been accelerated.

Taking a shock diameter of 30 Mm - this is the footpoint separation in the flare of 2003 Nov. 18 - and an angle between SMS and vertical of 5 $^{\circ}$ (this angle has to be small; cf. Aurass et al. 2002, and references therein), we obtain a distance of 170 Mm between diffusion region and TS. Assuming an outflow speed of $v_{\rm s}=1~852$ km s^-1 as given by our default parameters, a travel time of 92 s is found. This value is consistent with the observations, especially when bearing in mind that it actually represents the upper limit of the possible delay - a chromospheric flare ribbon signature probably needs some time to develop after the reconnection, which will reduce the observed delay.

The time lag between reconnection and acceleration still needs to be studied more systematically. It is well possible that the delay varies from event to event, dependent on factors such as flare size, geometry, shock parameters and efficiency of direct Joule heating of the chromosphere.

5 Conclusion

We have used a fully relativistic theory of shock drift acceleration (SDA; see Mann et al. 2009) to model electron acceleration at the reconnection outflow termination shock (TS) in solar flares. Our aim was to find out if this is a viable acceleration scenario for nonthermal electrons in solar flares. We have first discussed dynamic radio spectra, showing that non-drifting type II-like bursts actually represent signatures of termination shocks. In itself, this observation strongly supports the magnetic reconnection scenario of solar flares. From radio spectra and radioheliograms, we have derived some basic shock parameters, such as the upstream electron density and the shock area. We stress that this is one of the main benefits of considering the TS acceleration scenario: we have actual observations of the accelerator itself - the shock. This is not the case for both DC and stochastic acceleration.

RHESSI HXR spectra of 18 solar flares were used to obtain information on the injected electron fluxes, F(E), in particular with regard to total flux $F_{\rm tot}$ , kinetic power $P_{\rm tot}$ and power-law indices $\delta$ . A parametric study of the model was carried out in order to determine under which conditions the observations can be reproduced. The most basic quantities of the nonthermal electron fluxes are the total injected electron flux and the corresponding kinetic power. We found that $F_{\rm tot}=10^{36}$ s^-1 and $P_{\rm tot}=10^{29}$ erg s^-1 represent reasonable peak values in large flares. These values are reproduced by the model, provided that there is significant heating at the slow-mode shocks (i.e., $T \geq 20$ MK) and a sufficiently large shock area. Strong heating of the outflow is indeed predicted by theory, and the detection of Fe XXIV and X-ray emission above flaring loops is consistent with outflow temperatures of $T \geq 20$ MK.

For low electron densities upstream of the shock ( N₀ < 10⁹ cm^-3), as indicated by radiospectral observation, areas of the order of 10²⁰ cm² are required to reproduce the peak electron fluxes in the largest flares, unless temperature or compression are taken to very high values. These are big areas, but they are actually consistent with the source sizes obtained from radioheliographic observations. Significantly smaller areas are sufficient to power the late phase of long-duration events, where continuous heating is required (e.g. Harra-Murnion et al. 1998). Shocks at high densities ( $N_0 \approx 10^{10}$ cm^-3), which are not observable in radio, would require a maximum area of only a few times 10¹⁸ cm^-2, even in the impulsive phase. This is in agreement with the sizes of coronal above-the-looptop X-ray sources. The apparent discrepancy between radio-derived and SXR/HXR-derived shock size is not yet understood, and will require further study. In any case, we have shown that the model can reproduce the required fluxes both for a large-area/low-density and a small-area/high-density shock.

With regard to spectral shape, the SDA model does not produce true power-laws. While the energy-dependent spectral indices are in the right range between 10 and 100 keV (where the bulk of the energetic electrons resides), they soften too quickly above this range. However, we have not yet implemented effects such as multiple mirroring or preacceleration, which would all increase the electron fluxes at higher energies. It remains to be determined if these effects are sufficient to make the spectra consistent with observations.

The low-energy cutoffs of the synthetic spectra were found to be consistent with observations. The model predicts significantly higher fluxes and beam powers as are usually found from spectral fits, because in most cases the true low-energy cutoff is masked by thermal emission. This additional power is found to lie just in the range that is required to power white-light flares.

The SDA model is capable of reproducing the spectral evolution of flares. The relation between flux and spectral index is found to be consistent with observations, and both soft-hard-soft and soft-hard-harder evolutionary patterns can be modeled. Both the acceleration time at the shock and the temporal variation due to changing shock angles are short enough to reproduce the observed sub-second HXR bursts.

In this paper, we have developed the idea of shock drift acceleration at the termination shock into a quantitative and testable model. Detailed studies have shown that most observational constraints are fulfilled by the model, thus we conclude that SDA is an interesting possibility for electron acceleration in solar flares that certainly deserves further attention. The next question that will have to be addressed is whether it is possible to harden the electron flux spectra at higher energies. A further interesting topic will be SDA acceleration of protons and ions.

Acknowledgements

The work of A.W. was supported by D.L.R. under grant No. 50 QL 0001. The authors are grateful to the RHESSI Team (PI: R. P. Lin) for the free access to the RHESSI data and the development of the software. We thank F. Fárník for the provision of HXRS data. SOHO is a project of international cooperation between ESA and NASA. We gratefully acknowledge the use of Nançay Multifrequency Radioheliograph data.

References

Aschwanden, M. J., Schwartz, R. A., & Alt, D. M. 1995, ApJ, 447, 923 [NASA ADS] [CrossRef] (In the text)
Aschwanden, M. J., Wills, M. J., Hudson, H. S., et al. 1996, ApJ, 468, 398 [NASA ADS] [CrossRef] (In the text)
Aurass, H. 2007, Adv. Space Res., 39, 1407 [NASA ADS] [CrossRef] (In the text)
Aurass, H., & Mann, G. 2004, ApJ, 615, 526 [NASA ADS] [CrossRef] (In the text)
Aurass, H., Vrsnak, B., & Mann, G. 2002, A&A, 384, 273 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Aurass, H., Rausche, G., Mann, G., & Hofmann, A. 2005, A&A, 435, 1137 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Aurass, H., Mann, G., Rausche, G., & Warmuth, A. 2006, A&A, 457, 681 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Benz, A. O. 1987, Sol. Phys., 111, 1 [CrossRef] (In the text)
Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] (In the text)
Delaboudinière, J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162, 291 [NASA ADS] [CrossRef] (In the text)
Dulk, G. A., & McLean, D. J. 1978, Sol. Phys., 57, 235 (In the text)
Emslie, A. G., Dennis, B. R., Holman, G. D., & Hudson, H. S. 2005, JGR, 110, (In the text)
Fárník, F., Garcia, H., & Karlický, M. 2001, Sol. Phys., 201, 357 [NASA ADS] [CrossRef] (In the text)
Fletcher, L., Hannah, I. G., Hudson, H. S., & Metcalf, T. R. 2007, ApJ, 656, 1187 [NASA ADS] [CrossRef] (In the text)
Forbes, T. G. 1986, ApJ, 305, 553 [NASA ADS] [CrossRef] (In the text)
Grigis, P. C., & Benz, A. O. 2004, A&A, 426, 1093 [NASA ADS] [CrossRef] [EDP Sciences]
Gros, M., Tatischeff, V., Kiener, J., et al. 2004, in Proc. 5th INTEGRAL Workshop, ed. V. Schönfelder, ESA SP-552, 669 (In the text)
Harra-Murnion, L. K., Schmieder, B., van Driel-Gesztelyi, L., et al. 1998, A&A, 337, 911 [NASA ADS] (In the text)
Holman, G. D. 1985, ApJ, 293, 584 [NASA ADS] [CrossRef] (In the text)
Holman, G. D., & Pesses, M. E. 1983, ApJ, 267, 837 [NASA ADS] [CrossRef] (In the text)
Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] (In the text)
Kerdraon, A., & Delouis, J. 1997, in Coronal Physics from Radio and Space Observations, ed. G. Trottet (Heidelberg: Springer), 192 (In the text)
Kiener, J., Gros, M., Tatischeff, V., Weidenspointer, G. 2006, A&A, 445, 725 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kiplinger, A. L. 1995, ApJ, 453, 973 [NASA ADS] [CrossRef] (In the text)
Kontar, E. P., & MacKinnon, A. L. 2005, Sol. Phys., 227, 299 [NASA ADS] [CrossRef] (In the text)
Kontar, E. P., Emslie, A. G., & Piana, M. 2005, Sol. Phys, 226, 317 [NASA ADS] [CrossRef] (In the text)
Lin, R. P., & Hudson, H. S. 1976, Sol. Phys., 50, 153 [NASA ADS] (In the text)
Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [NASA ADS] [CrossRef] (In the text)
Lin, R. P., Krucker, S., Hurford, G. J., et al. 2003, ApJ, 595, L69 [NASA ADS] [CrossRef] (In the text)
Litvinenko, Y. E. 2003, in Energy Conversion and Particle Acceleration in the Solar Corona, ed. K.-L. Klein (Springer) LNP 612, 213 (In the text)
Maksimovic, M., Pierrard, V., & Lemaire, J. 1997, A&A, 324, 725 (In the text)
Mann, G., Aurass, H., Voigt, W., & Paschke, J. 1992, ESA SP-348, 129 [NASA ADS] (In the text)
Mann, G., Classen, T., & Aurass, A. 1995, A&A, 295, 775 [NASA ADS] (In the text)
Mann, G., Classen, T., & Motschmann, U. 2001, JGR, 106 (In the text)
Mann, G., Aurass, H., & Warmuth, A. 2006, A&A, 454, 969 [CrossRef] [EDP Sciences] (In the text)
Mann, G., Warmuth, A., & Aurass, H. 2009, A&A, 494, 669 [CrossRef] [EDP Sciences] (In the text)
Masuda, S., Sato, J., Kosugi, T., & Sakao, T. 2000, Adv. Space Res. 26, 493 [NASA ADS] (In the text)
Melrose, D. B. 1994, ApJS, 90, 623 [NASA ADS] [CrossRef] (In the text)
Mercier, C., Subramanian, P., Kerdraon, A., et al. 2006, A&A, 447, 1189 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Miklenic, C. H., Veronig, A. M., Vrsnak, B., & Hanslmeier, A. 2007, A&A, 461, 697 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Miller, J. A., Cargill, P. J., Emslie, A. G., et al. 1997, JGR, 102, 14631 [NASA ADS] [CrossRef] (In the text)
Nelson, G. S., & Melrose, D. 1985, in Solar Radiophysics, ed. D. J. McLean, & N. R. Labrum (Cambridge: Cambridge University Press), 333 (In the text)
Newkirk, G. A. 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] (In the text)
Nitta, N. V., Sato, J., & Hudson, H. 2001, ApJ, 552, 821 [NASA ADS] [CrossRef] (In the text)
Parks, G. K., & Winckler, J. R. 1969, ApJ, 155, 117 [NASA ADS] [CrossRef] (In the text)
Priest, E. R. 1982, Solar magnetohydrodynamics (Dordrecht: Reidel Publ. Co.) (In the text)
Rausche, G., Aurass, H., Mann, G., et al. 2007, Sol. Phys., 245, 327 [NASA ADS] [CrossRef] (In the text)
Saint-Hilaire, P., & Benz, A. O. 2005, A&A, 435, 743 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Sato, T., & Hayashi, T. 1979, Phys. Fluids, 22, 1189 [NASA ADS] [CrossRef] (In the text)
Selkowitz, R., & Blackman, E. G. 2007, MNRAS, 379, 43 [NASA ADS] [CrossRef] (In the text)
Shibata, K., Masuda, S., Shimojo, M., et al. 1995, ApJ, 451, L83 [NASA ADS] (In the text)
Smerd, S. F., Sheridan, K. V., & Stewart, R. T. 1975, ApL, 16, 23 (In the text)
Sui, L., & Holman, G. D. 2003, ApJ, 596, L251 [NASA ADS] [CrossRef] (In the text)
Sui, L., Holman, G. D., & Dennis, B. R. 2004, ApJ, 612, 546 [NASA ADS] [CrossRef] (In the text)
Sui, L., Holman, G. D., & Dennis, B. R. 2007, ApJ, 670, 862 [NASA ADS] [CrossRef] (In the text)
Tanuma, S., & Shibata, K. 2005, ApJ, 628, L77 [NASA ADS] [CrossRef] (In the text)
Tsuneta, S., & Naito, T. 1998, ApJ, 495, L67 [NASA ADS] [CrossRef] (In the text)
Tsuneta, S., Masuda, S., Kosugi, T., & Sato, J. 1997, ApJ, 478, 787 [NASA ADS] [CrossRef] (In the text)
Vocks, C., Mann, G., & Rausche, G. 2008, A&A, 480, 527 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Vrsnak, B., & Skender, M. 2005, Sol. Phys., 226, 97 [NASA ADS] [CrossRef] (In the text)
Vrsnak, B., Aurass, H., Magdalenic, J., & Gopalswamy, N. 2001, A&A, 377, 321 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Wang, T., Sui, L., & Qiu, J. 2007, ApJ, 661, L207 [NASA ADS] [CrossRef] (In the text)
Warmuth, A., & Mann, G. 2005, A&A, 435, 1123 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Warren, H. P., & Reeves, K. K. 2001, ApJ, 554, L103 [NASA ADS] [CrossRef] (In the text)

Footnotes

...B: Note that for the purpose of comparison with the observed values, 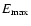$E_{\max}$ is actually the more relevant parameter because it is comparable to the cutoff energy in the ``turnover'' model.

All Figures

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig1.eps}\end{figure}$	Figure 1: Top: dynamic radio spectrum (Tremsdorf radiospectrograph) showing the impulsive phase of the X1.7 flare of 2001 Mar. 29. Around 300 MHz a slowly drifting TS signature is visible starting at 10:04 UT. Bottom: HXR count rates in the energy channels (from above) 67-100, 100-147, and 147-220 keV as given by the HXRS instrument for the corresponding time range. Note the temporal correlation with the TS signature.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig2.eps}\end{figure}$	Figure 2: Radio source of the TS in the X1.7 flare of 2001 Mar. 29 imaged by NRH. The background image shows the flaring active region in EUV (SOHO/EIT) at 10:13:20 UT. The white contours show the TS source at 327 MHz and 10:05:24 UT, while the dashed black contours show the TS at 237 MHz and 10:08:44 UT. The white ellipse in the upper left corner shows the NRH beam at 327 MHz.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig3.eps}\end{figure}$	Figure 3: RHESSI HXR photon spectrum for the X4.8 flare of 2002 Jul. 23, integrated over the period of 00:26:40-00:27:00 UT. The background-subtracted photon flux (plus signs; the background is shown by the horizontal bars) is plotted as a function of photon energy in units of keV and is fitted with a thermal bremsstrahlung contribution from an isothermal plasma (dotted curve) and a double power-law nonthermal electron flux component with a low-energy cutoff (dashed line). The best-fit parameters are shown in the plot.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig4.eps}\end{figure}$	Figure 4: RHESSI HXR light curves and time series of fit parameters for the X4.8 flare of 2002 Jul. 23. Shown are count rates in three energy bands, spectral indices (crosses denote $\delta _{\rm L}$ and diamonds refer to $\delta _{\rm H}$ ), break energy, low-energy cutoff, total flux and total kinetic power (both integrated over all energies above the low-energy cutoff) of the injected nonthermal electrons.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig5.eps}\end{figure}$	Figure 5: Total kinetic power $P_{\rm tot}$ versus total flux $F_{\rm tot}$ of the injected nonthermal electrons as obtained from thick-target fits of 1053 RHESSI spectra observed in 18 solar flares.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=4cm,clip]{fig6.eps}\end{figure}$	Figure 6: Geometry of SDA at the TS. Magnetic field lines are reconnected in the diffusion region (DR) and two outflow jets are formed. The inflow is separated from the outflow by two pairs of slow-mode standing shocks (SMS). In the reconnection outflow jets fast-mode termination shocks (TS) have formed (only the lower one is shown). For details see main text.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{101fig7.eps}\hspace*{7mm} \includegraphics[width=8cm,clip]{101fig8.eps}\end{figure}$	Figure 7: Left: integrated nonthermal electron flux density $j_{\rm tot}$ (top) and kinetic power density $P_{\rm tot}/A_{\rm s}$ (bottom) as a function of $\theta_{\min}$ . Right: corresponding acceleration efficiency (top), defined as the ratio of $j_{\rm tot}$ to the total incoming flux density, and shock fraction (bottom), which is the fraction of the shock area where SDA is valid. Crosses represent $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ and acceleration efficiency integrated over all energies, diamonds, triangles and squares represent these quantities above a low-energy cutoff of 10, 20, and 30 keV, respectively.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig9.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig10.eps} } \end{figure}$	Figure 8: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of X.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=8cm]{101fig11.eps}\hspace{1cm} \includegraphics[width=8cm]{101fig12.eps} } \end{figure}$	Figure 9: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of N₀.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig13.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig14.eps} } \end{figure}$	Figure 10: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of T.
Open with DEXTER
In the text

$\begin{figure} \par\mbox{\includegraphics[width=8cm,clip]{101fig15.eps}\hspace{1cm} \includegraphics[width=8cm,clip]{101fig16.eps} } \end{figure}$	Figure 11: As in Fig. 7, but showing $j_{\rm tot}$ , $P_{\rm tot}/A_{\rm s}$ , acceleration efficiency and shock fraction as a function of B₀.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig17.eps}\end{figure}$	Figure 12: Top: injected electron flux density spectrum j(E) as given by the shock-drift acceleration model using the default values for the input parameters (given in the figure). Bottom: corresponding spectral index $\delta (E)$ as a function of energy. The dotted curves in both plots show j(E) and $\delta (E)$ of the initial Maxwellian distribution for comparison.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{101fig18.eps}\end{figure}$	Figure 13: As in Fig. 12, but showing j(E) and $\delta (E)$ resulting from SDA acceleration acting on an initial Kappa distribution with $\kappa =10$ (dotted curves).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig19.eps}\end{figure}$	Figure 14: Plot of electron spectral index $\delta$ versus electron flux at 60 keV, F₆₀. Black dots are values derived from 1053 fitted RHESSI spectra, while the colored symbols represent the model results for a variation of the input parameters $\theta_{\min}$ , X, N₀, and T, as well as for a variation of B₀. Arrowheads indicate the direction in which each parameter increases.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{101fig20.eps}\end{figure}$	Figure 15: Accelerated electron flux density for a single field line, $j_{\rm bin}$ , integrated over four energy bins (given in the figure) as a function of time.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.