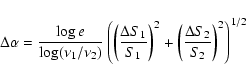Physical properties of very powerful FRII radio galaxies

C. P. O'Dea; R. A. Daly; P. Kharb; K. A. Freeman; S. A. Baum

doi:10.1051/0004-6361:200809416

Free Access

Issue		A&A Volume 494, Number 2, February I 2009


Page(s)		471 - 488
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361:200809416
Published online		07 October 2008

Physical properties of very powerful FRII radio galaxies

C. P. O'Dea¹ - R. A. Daly² - P. Kharb³ - K. A. Freeman² - S. A. Baum³

1 - Department of Physics, Rochester Institute of Technology, 54 Lomb Memorial Drive, Rochester, NY 14623, USA
2 - Department of Physics, Penn State University, Berks Campus, PO Box 7009, Reading, PA 19610, USA
3 - Center for Imaging Science, Rochester Institute of Technology, 54 Lomb Memorial Drive, Rochester, NY 14623, USA

Received 17 January 2008 / Accepted 25 September 2008

Abstract
Aims. We estimate the ages and physical properties of powerful radio galaxies.
Methods. An analysis of new multi-wavelength VLA observations of eleven very powerful classical double (FRIIb) radio galaxies with redshifts between 0.4 and 1.3 is presented. We estimate ages and velocities for each side of each source. The eleven new sources are combined with previously studied samples and the characteristics of the full sample of 31 sources are studied; the full sample includes sources with redshifts between 0.056 and 1.79, and core-hot spot sizes of about 30 to 400 kpc.
Results. The velocities are independent of core-hotspot separation, suggesting the rate of growth of a given source is roughly constant over the source lifetime. We combine the rate of growth, width, and pressure of a source to study the beam power, lifetime, energy, and ambient gas density using standard methods previously applied to smaller samples. Typical beam powers are in the range from 10⁴⁴ to 10⁴⁶ erg/s; we show that this quantity is insensitive to assumptions regarding minimum energy conditions. The beam powers are independent of core-hotspot separation suggesting that the beam power of a given source is roughly constant over the source lifetime. Typical total source lifetimes are found to be about a few $\times$ (10⁶-10⁷) years, and typical total outflow energies (E/c²) are found to be about 5 $\times$ $(10^5{-}10^6)~M_{\odot}$ . Ambient gas densities are found to decrease with increasing core-hotspot distance, but have no redshift dependence. Overall, the results obtained with the sample of 31 sources studied here are consistent with those obtained earlier with smaller samples.

Key words: galaxies: active - galaxies: jets - galaxies: intergalactic medium

1 Introduction

Radio galaxies are beacons that pinpoint sites of active nuclei of galaxies containing the most massive black holes. They provide important information on the properties of the active nuclei, the large-scale environments of these distant galaxies, and the interaction between outflows from active nuclei and the source environment. In this paper, we focus on the properties of very powerful classical double radio galaxies, referred to as FRIIb sources.

Classical double radio sources, also known as FRII sources (Fanaroff & Riley 1974), exhibit a variety of structures. Leahy & Williams (1984) identified five types of FRII sources including sources with no bridge distortion (type 1) and four types of bridge distortion (types 2-5). Leahy et al. (1989) found a correlation between radio bridge (also called lobe) structure and radio power: the most powerful classical double radio galaxies, those with 178 MHz radio powers greater than about 3 h^-2 $\times$ 10²⁶ W/Hz/sr, have quite regular bridge structure, that is, they have type 1 bridge structure. The regular radio bridge structure of these very high power classical double radio galaxies was taken as an indication that back flow was likely to be negligible in these sources. Given that FRII sources can be divided into those with regular radio bridge structure, type 1 of Leahy & Williams (1984), and those with distorted radio bridge structure, types 2-5 of Leahy & Williams (1984), Daly (2002) divided the sources into types FRIIa and FRIIb based on the power dependence found by Leahy et al. (1989). Thus, Daly (2002) defined FRII sources with 178 MHz radio powers greater than about 3 h^-2 $\times$ 10²⁶ W/Hz/sr as FRIIb sources, and all FRII sources with lower power to be FRIIa sources. It is the FRIIb sources that have high radio power and regular radio bridge structure, and thus are likely to have negligible back flow in the radio bridge region.

Only FRIIb sources are included in the present study. Thus, most of the sources are found at relatively high redshift; only a few local sources belong to this population. An estimate of source age is presented for 11 new radio sources, as discussed in Sect. 2. The new sources are combined with previously studied samples of 14 and 6 radio galaxies to form a sample of 31 sources. The physical properties of the sample of 31 radio sources such as the source velocities, pressures, widths, beam powers, ambient gas densities, lifetimes, and energies are discussed in Sect. 3, and the results are summarized in Sect. 4. Throughout the paper, we assume a Lambda Cold Dark Matter cosmology with the standard cosmological parameters $\Omega_{\rm m}$ = 0.3 and $\Omega_{\Lambda}$ = 0.7, and a value of Hubble's constant of H₀ = 70 km s^-1 Mpc^-1.

2 Estimates of source age for the new sample of eleven radio galaxies

In the current paradigm (the ``standard model'') for classical double radio galaxies supersonic jets propagate outwards through the ambient medium (e.g., Blandford & Rees 1974; Scheuer 1974; Leahy et al. 1989; Begelman & Cioffi 1989; Daly 1990; Leahy 1991). The energy of the jets is thermalized in a terminal shock (called the hotspot). X-ray observations show that particle acceleration occurs in the hot spots (e.g., Hardcastle et al. 2007). The shocked jet material flows sideways from the hot spots to inflate a cocoon (called the radio lobes or bridges). This cocoon material is left behind as the jet continues to push forwards. Radiative losses will steepen the radio spectrum (e.g., Kardashev 1962; Pacholczyk 1970; Alexander 1987) with increasing distance from the acceleration site (e.g., Burch 1977). Thus, multi frequency radio imaging can allow the spectral steepening to be measured, and in the context of the standard model, the source age and overall advance speed to be estimated. Note that it is the radio spectral index, and not the radio flux density at one given frequency, that enters into the spectral aging approach. The sources are considered to have a region in which the electrons are accelerated to very high energies (identified with the hot spot and its immediate vicinity), and regions in which these electrons age significantly due to synchrotron and inverse Compton losses (identified as regions distinct from the acceleration site, that is, regions in the radio lobe).

Many multi-wavelength studies of radio sources have shown that this approach gives reasonable estimates of source ages (e.g., Myers & Spangler 1985; Alexander 1987; Alexander & Leahy 1987; Leahy et al. 1989; Carilli et al. 1991; Liu et al. 1992; Mack et al. 1998; Guerra et al. 2000; Jamrozy et al. 2008). Observations at 90 GHz of some radio sources show spectral steepening consistent with the expectations of spectral aging models (Hardcastle & Looney 2008). Studies of large radio sources show that spectral aging analyses give source ages that are in good agreement with estimates based on dynamical models (e.g., Parma et al. 1998; Murgia et al. 1999; Kaiser 2000; Machalski et al. 2007). VLBI studies of hot spot proper motions in compact radio sources give direct measurements of dynamical ages which are in good agreement with estimates from spectral aging (e.g., Polatidis & Conway 2003; Murgia 2003; Nagai et al. 2006; Orienti et al. 2007). These studies indicate that spectral aging analysis provides a useful estimate of the source age.

2.1 The injection spectral index

The injection spectral index is the spectral index the electrons have in and around the acceleration site (the hot spot and its immediate vicinity). We combined snapshot data from the A and C configurations at 20 cm, and from the B and D configurations at 6 cm to give us sensitivity to structure on a range of size scales with a nominal resolution of about 1.2 arcsec (Kharb et al. 2008). In order to optimize the quality of the maps and our sensitivity to spectral index gradients in the low surface brightness lobe emission we tapered the uv data to achieve a resolution of between 2-2.5 arcsec. The spectral index maps used are shown in Figs. 51.1, and 51.3 through 51.12 of the electronic version of Kharb et al. (2008), and each figure includes an insert showing the beam size.

As expected for hot spots of powerful radio galaxies (e.g., Black et al. 1992; Hardcastle et al. 2007), our sources show sub-arcsecond scale structure in the hot spots (see the 8.4 GHz images at $\sim$ 0.25 arcsec resolution in Kharb et al. 2008). Thus, the 2-2.5 arcsec resolution images used here will average over substructure in the hot spots. In order to indicate how much substructure is included in our estimates of the injection spectral index, we show the $\sim$ 0.25 arcsec resolution 8.4 GHz images of the hot spots in Figs. 1-21 (available in the electronic version) with two circles centered on the peak brightness of the hot spot. One circle has a diameter equal to our CLEAN beam FHWM (between 2 and 2.5 arcsec) and one has a diameter equal to 1 arcsec.

Table 1: Comparison of hot spot spectral indices.

One potential concern is that the spectral index we determine for the hot spot and vicinity (and thus the injection index) is affected by the substructure which we include, or perhaps by lobe emission where the hot spot is seen projected against the lobe. To check this, we remade the images with a CLEAN restoring beam of 1.0 arcsec, calculated the 1.4 to 4.8 GHz spectral index image, and determined the spectral index for the hot spot. The 1 arcsec beam is close to the nominal 1.2 arcsec and so is not a large extrapolation of our data. The 1 arcsec CLEAN beam has an area which is at least 4 times less than that of the 2-2.5 arcsec resolution data and thus the contribution to each beam from extended emission would be lower by that factor of 4. Table 1 shows that the hot spot spectral indices determined at the two resolutions (1 arcsec and 2-2.5 arcsec) are consistent with each other - i.e., there is no significant offset, but a scatter of about 0.1. Thus, we conclude that the spectral index measurements of the hot spots are not significantly affected by including hot spot sub-structure or faint emission from the lobes on scales between $\sim$ 1-2 arcsec. In addition, we note that the spectral index of the lobe emission near the hot spot is close to that of the hot spot itself (as indicated in the analysis described above, and shown in Figs. 51.1, and 51.3 through 51.12 of the electronic version of Kharb et al. 2008). This is presumably because the lobe material near the hot spot has not experienced substantial radiative aging.

Leahy et al. (1989) used the 151 MHz to 1.5 GHz hot spot spectral index obtained at resolutions of 3 to 4 arcsec as the injection index, and Liu et al. (1992) used the 38 MHz to 1 GHz spectral index integrated over the source as the injection index. The data of Liu et al. (1992) were analyzed by Wellman et al. (1997, hereafter WDW) who used the 1.4 to 5 GHz hot spot spectral index obtained at about 1.2 arcsec resolution as the injection index and showed that the spectral aging results were in very good agreement with those obtained by Liu et al. (1992). Thus, the two approaches are consistent, suggesting that at low frequencies, the electrons have not experienced significant radiative losses and the spectral index is that of the original injection spectrum.

In Table 1 we compare our 20-6 cm hot spot spectral indices with the 38 MHz to 1.4 GHz spectral indices based on integrated flux densities, which is similar to the approach of Liu et al. (1992). We see that there are no significant offsets (i.e., one is not systematically steeper than the other), but there is a scatter of about 0.1. Thus, our hot spot spectral indices measured between 1.4 and 4.8 GHz are consistent with those measured (for the whole source) at low frequencies (38 MHz to 1.4 GHz) and are a useful measure of the injection spectrum. Because both of these comparisons result in scatter of about 0.1, we adopt this value as a conservative estimate of the possible contribution of systematic errors to the spectral index measurements.

As an additional consistency check, we note that the hotspot spectral index is correlated with the lobe spectral index and is flatter than the lobe spectral index (Fig. 2 of Kharb et al. 2008), as expected if the spectra of the radiating electrons steepen after they leave the hot spot.

2.2 Estimating source age

To estimate the source ages, we followed the procedure outlined by Leahy et al. (1989). The spectral age is characterized by a break frequency $\nu_T$ . The source age t is given by

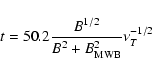$\begin{displaymath}% t = 50.2 {B^{1/2} \over B^2 + B_{\rm MWB}^2 } \nu_T^{-1/2} \end{displaymath}$

(1)

where t is in Myr, B and $B_{\rm MWB}$ are in units of $10~\mu$ G, $\nu_T$ is in GHz and is simply related to the observed break frequency $\nu_{0T}$ , $\nu_T = \nu_{0T}(1+z)$ , and $B_{\rm MWB} = 3.18(1+z)^2$ $\mu$ G is the equivalent magnetic field strength of the cosmic microwave background (Jaffe & Perola 1973). The minimum energy magnetic field strength is obtained using the expression of Miley (1980) assuming no relativistic protons, a filling factor of unity, a tangled magnetic field, cylindrical symmetry with random orientation to the line of sight, and a power-law spectrum with cutoffs at 10 MHz and 100 GHz. The expected spectral index for a given injection spectral index as a function of break frequency was computed by numerically integrating the equations given by Meyers & Spangler (1985). Meyers & Spangler showed that the spectral index between two frequencies near the break was sufficient to allow estimation of the break frequency. We performed the Myers & Spangler calculations for both the Kardashev-Pacholczyk (KP) and Jaffe-Perola (JP) models. They give similar results and we quote the results for the JP model.

Total intensity maps at 20 and 6 cm at matched angular resolutions of 2 to 2.5 arcsec with circular Gaussian restoring beams were corrected for the primary beam attenuation and were used to obtain the spectral index maps. The spectral index between two frequencies $\nu_1$ and $\nu_2$ is given by

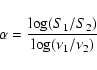$\begin{displaymath}% \alpha = {\log (S_1/S_2) \over \log(\nu_1/\nu_2) } \end{displaymath}$

(2)

where S₁ and S₂ are the respective flux densities. The error in the spectral index is given by

$\begin{displaymath}% \Delta \alpha = { \log e \over \log (\nu_1/\nu_2) } \left( ... ...right)^2 + \left({\Delta S_2 \over S_2}\right)^2 \right)^{1/2} \end{displaymath}$

(3)

where $\Delta S_1$ and $\Delta S_2$ are the one sigma errors in the flux densities. The errors in flux density includes a contribution from the thermal noise due to the sensitivity of the array which is straightforward to determine (e.g., Crane & Napier 1985) plus additional contributions whose magnitude is difficult to determine e.g., the missing uv spacings, and problems with the calibration, self-calibration, and deconvolution processes (e.g., Perley 1985; Leahy et al. 1989). To account for the additional flux density errors, we adopted values for $\Delta S_1$ and $\Delta S_2$ that were factors of three larger than the rms noise in the image at locations far from the source. However, the hot spots are so bright, that even with the conservative values of $\Delta S$ , the calculated values of $\Delta \alpha$ are very small. So as discussed in Sect. 2.1 we adopted an additional conservative upper limit for the uncertainty in the spectral index of $\Delta \alpha = 0.1$ We also blanked the images at values less than 3 times the rms noise determined at distances far from the source.

Table 2: Estimates of ages of the eleven radio galaxies.

Following the work on Leahy et al. (1989), Liu et al. (1992), and WDW, the spectral index gradient is measured between the hot spot and one lobe position for each side of each source; in the Appendix, it is shown that very similar results are obtained by measuring the spectral gradient between many points on each side of each source. The lobe position was chosen to be in a region of high signal to noise, and far from the hot spot so that a significant spectral index difference existed between the hot spot and the lobe. The break frequency was determined by comparing the observed spectral index difference with the calculations of the JP model using the Myers & Spangler method. The one sigma range of the spectral index difference was used to obtain the uncertainty of the break frequency. The age of the electrons was obtained using Eq. (1), with the magnetic field strengths described in Sect. 3.2; the best fit parameters are listed in Table 2. Using the age and the distance from the hot spot, the rate of growth of each side of each source (the expansion velocity) is obtained, and is listed in Table 3. In the Appendix, velocities are determined at multiple locations on each side of each source. It turns out that these velocities are in very good agreement with those obtained here and listed in Table 3.

Table 3: Summary of source properties.

3 Physical parameters of the combined sample of 31 radio galaxies

The physical parameters of the new sample of 11 radio galaxies of Kharb et al. (2008) are combined with those published earlier for samples of 6 (Guerra et al. 2000) and 14 radio galaxies (Leahy et al. 1989; Liu et al. 1992; WDW) to yield a sample of 31 radio galaxies. Parameters are determined for each side of each source, though two sources (3C 239 and 3C 324) only had radio bridge data on one side of the source, so we study a total of 60 radio bridges.

Table 4: Summary of source properties. II.

The lobe propagation velocity for each side of each source is presented and discussed in Sect. 3.2 and listed in Table 3. Converting the velocity from the cosmological model adopted for the earlier studied samples of 6 and 14 radio galaxies to that adopted here is non-trivial, so these are listed in Table 3 for the cosmology adopted here. Beam powers, ambient gas densities, total source lifetimes, and total source energies are obtained for the new sample of 11 sources and combined with those published earlier for the samples of 6 and 14 sources. The results obtained for the full sample are presented in Sects. 3.3-3.6 respectively.

3.1 Projection effects

In this study, radio galaxies are considered so as to minimize projection effects. If the sources are not in the plane of the sky, our estimated velocities will be lower limits to the true velocity, e.g., a source which is oriented 30 degrees from the plane of the sky will have a velocity 15% larger than our estimate. Projection effects were studied in detail by Wan & Daly (1998), and are found to be quite small for the quantities studied here except when the outflow axis of the source is quite close to the line of sight of the observer.

In Kharb et al. (2008), we showed that several diagnostics of alignment and Doppler boosting were consistent with the eleven galaxies studied here lying close to the plane of the sky. The UV/optical spectra show that these are all narrow-line radio galaxies, which suggests that they are oriented at angles >45 degrees to the line of sight, under the standard Unified scheme (e.g., Barthel 1989; Urry & Padovani 1995).

We noted that the ratio of the angular extent of the larger radio lobe (distance between hotspot and core) to the smaller one, known as the arm-length ratio (Q), was $\sim$ 1.1 for the majority of the radio galaxies, with only three galaxies exhibiting ratios >1.5 (3C 44 (1.6), 3C 54 (1.8) and 3C 441 (2.4)). Assuming that the jets are intrinsically symmetric and any apparent asymmetry is due to the difference in light travel times between the two sides (e.g., Longair & Riley 1979; Kapahi & Saikia 1982) and using the relation $Q=(1+\beta \cos \theta)/(1-\beta \cos \theta)$ , an arm-length ratio of 1.1 would give a $\beta \cos \theta$ of 0.047 or $\theta$ = 62 degrees relative to the line of sight for $\beta$ = 0.1 (e.g., Bridle & Perley 1984).

Another statistical indicator of beaming/orientation is the radio core prominence parameter ( $R_{\rm c}$ , Orr & Browne 1982), which is the ratio of the (beamed) core to the (unbeamed) extended flux density (see Appendix C, Urry & Padovani 1995). For these radio galaxies, $-4.3 < \log R_{\rm c} < -2.5$ (Kharb et al. 2008). Kharb & Shastri (2004) estimated the $R_{\rm c}$ values (which are linearly correlated with $\theta$ ) for a large sample of radio galaxies and their respective beamed counterparts (see Fig. 3 of Kharb & Shastri). Assuming that these sources are randomly oriented in the sky and span the entire $\theta$ range (0 to 90 degrees), a comparison with Fig. 3 indicates that our eleven galaxies lie at angles larger than 60 degrees to the line of sight, or within 30 degrees of the plane of the sky.

For sources lying at small angles to line of sight, intrinsic misalignment between the jet and counter-jet appears to get amplified (e.g., Kapahi & Saikia 1982). The observed misalignment ( $\zeta$ ) is related to the intrinsic misalignment ( $\zeta_{\rm int}$ ), by $\sin(\theta) = \tan(\zeta_{\rm int})/\tan(\zeta)$ , for the simplified case in which the azimuth of the jet bending is $90\hbox{$^\circ$ }$ (see Appl et al. 1996). We found that the jet and counter-jet were misaligned by less than 5 degrees for the majority of our radio galaxies, with only one galaxy showing a misalignment >10 degrees (3C 169.1 (15 degrees)). If we adopt an intrinsic misalignment angle of $\sim$ $4\hbox{$^\circ$ }$ (e.g., Appl et al. 1996), this would imply a jet orientation angle $\theta > 50\hbox{$^\circ$ }$ relative to the line of sight for the majority of the radio galaxies.

As seen in Fig. 5 of Kharb et al. (2008), the lobe-to-lobe differences in depolarization are not correlated with either the radio core prominence or the misalignment angle. In other words, we do not find evidence for the ``Laing-Garrington effect'' (Garrington et al. 1988; Laing 1988) in our radio galaxies. The lack of a correlation is consistent with the picture of these radio galaxies lying close to the plane of the sky. This is also consistent with the fact that all these galaxies lack bright one-sided jets, typically observed in quasars.

The fact that all of the sources are narrow-line radio galaxies, and have arm-length ratios close to unity, low radio core prominence parameters, small misalignments between the jet and counter-jet, and do not exhibit the Laing-Garrington effect all suggest that the sources are within about 30 degrees of the plane of the sky.

3.2 Velocities

The velocities are obtained using the spectral age given by Eq. (1) and the separation $\theta$ between the hotspot and the location where $\alpha_{\rm final}$ was measured. The average minimum energy magnetic field strength in the radio lobe region was obtained in a manner identical to that used earlier so the new results can be combined with those obtained previously; thus, $B_{\rm min}$ in the radio lobe region was taken to be (B₁₀B₂₅)^0.5, where B₁₀ and B₂₅ are the minimum energy magnetic field strengths at distances of 10 and 25 h^-1 kpc behind the hotspot (toward the core). In addition to considering a magnetic field strength given by the minimum energy value $B_{\rm min}$ , we also consider the possibility that the magnetic field strength is less than the minimum energy value by a factor of 4, so $B = 0.25 B_{\rm min}$ , parameterized by $b = B/B_{\rm min}$ . This is the same offset that was studied previously, and thus provides a good comparison to results obtained previously, and there are good reasons for this choice, as described below.

An offset from minimum energy conditions was suggested by Carilli et al. (1991) for Cygnus A and Perley & Taylor (1991) for 3C 295 to obtain agreement between the ambient gas density indicated by X-ray observations and that indicated by the ram pressure confinement of the forward region of the radio lobe (see also De Young 2002). WDW showed that the dispersion in the offset is likely to be less than about 15% for very powerful radio galaxies of the type studied here.

Note that only FRIIb radio galaxies are included in the study. These sources have very regular bridge structure suggesting that back flow is not important in these sources (Alexander & Leahy 1987; Leahy et al. 1989; WDW; Kaiser 2000; Daly 2002), and that the sources are growing at a rate that is well into the supersonic regime. As described by Alexander & Leahy (1987) and Leahy et al. (1989), significant back flow will collide with the relativistic plasma in the bridge causing side flows and bridge distortions. As shown by Machalski et al. (2007), a spectral aging analysis of radio sources provides a reliable parametric fit to the source age.

The overall rate of growth or lobe propagation velocity is listed for each source for b=0.25 and b=1 in Table 3 and shown in Figs. 22 and 23 as functions of core-hotspot distance and in Figs. 24 and 25 as functions of redshift. When a value of b=0.25 is taken, a fractional error in b of 15% is included in the uncertainties of the velocity, pressure, and beam power. When a value of b = 1 is taken, no uncertainty in b is propagated through other quantities. Typically, the difference in the total error is not strongly affected by the uncertainty in b. Several previous studies of spectral aging have obtained velocities assuming b=1 with no uncertainty in this quantity. Thus, the values and uncertainties of v we obtain with b=1 can be directly compared with those obtained by other groups, and, to illustrate the effect of including the uncertainty of b on the uncertainty of v, this is included for the case b=0.25.

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f22.ps} \end{figure}$	Figure 22: Source advance velocity v/c as a function of core-hotspot distance r for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f23.ps} \end{figure}$	Figure 23: Source advance velocity v/c as a function of core-hotspot distance r for b=0.25.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f24.ps} \end{figure}$	Figure 24: Source advance velocity v/c as a function of redshift (1+z) for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f25.ps} \end{figure}$	Figure 25: Source advance velocity v/c as a function of redshift (1+z) for b=0.25.
Open with DEXTER

The velocities obtained do not correlate with core-hotspot separation, as indicated in Tables 5 and 6; this result is also obtained in the Appendix. This suggests that the velocity of a particular source is roughly constant over the lifetime of that source. The velocities do not correlate with redshift, suggesting that no redshift dependent selection effects or systematic errors are skewing the synchrotron ages.

Table 5: Fits to the data (b = 0.25).

Table 6: Fits to the data (b = 1).

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f26.ps} \end{figure}$	Figure 26: Pressure in the lobe P measured at 10 h^-1 kpc from the hotspot toward the central region of the source, as a function of core-hotspot distance r for b = 0.25. The pressure for b=1 is lower by a factor of 0.218 since P(b=1) = 0.218 P(b=0.25).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f27.ps} \end{figure}$	Figure 27: Pressure in the lobe P measured at 10 h^-1 kpc from the hotspot toward the central region of the source, as a function of (1 + z) for b = 0.25. The pressure for b=1 is lower by a factor of 0.218 since P(b=1) = 0.218 P(b=0.25).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f28.ps} \end{figure}$	Figure 28: Beam power L_j as a function of core-hotspot distance r for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f29.ps} \end{figure}$	Figure 29: Beam power L_j as a function of core-hotspot distance r for b=0.25.
Open with DEXTER

Thus, we find that propagation speeds of powerful radio galaxies on scales of tens to hundreds of kpc are independent of source size or redshift. This is consistent with the results of observational, analytical, and numerical simulation studies of radio galaxy evolution which suggest that large radio sources propagate at roughly constant velocity (e.g., Fanti et al. 1995; Neeser et al. 1995; Begelman 1996; Kaiser & Alexander 1997; Kaiser et al. 1997; De Young 1997; O'Dea & Baum 1997; Blundell et al. 1999; Snellen et al. 2000; Alexander 2000; De Young 1997; Carvalho & O'Dea 2002a,b).

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f30.ps} \end{figure}$	Figure 30: Beam power L_j as a function of redshift (1+z) for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f31.ps} \end{figure}$	Figure 31: Beam power L_j as a function of redshift (1+z) for b=0.25.
Open with DEXTER

3.3 Beam powers

The beam power of a source may be estimated based on the rate of growth of the source, v, the pressure in the radio bridge, P, and the cross-sectional width of the bridge, a, as described, for example, by Daly (1990) and Rawlings & Saunders (1991). Here, we use Eqs. (2) and (3) of Wan et al. (2000), who show that L_j = 3.6 $\times$ $10^{44} (a/{\rm kpc})^2 (v/c)(P/(10^{-10}~{\rm dynes~cm}^{-2}))~{\rm erg~s}^{-1}$ and $P=[(4/3)b^{-1.5}+b^2](B_{\rm min}/24\pi)$ , so $P(b=1.0)\approx 0.218 P(b=.25)$ . Widths and pressure for the 11 new sources were obtained in a manner identical to the way they were obtained for the previously studied samples of 6 and 14 radio galaxies (see WDW and Wan et al. 2000). The lobe pressure as a function of core - hot spot separation and redshift are shown in Figs. 26 and 27, respectively. Values of L_j obtained for the sample are listed in Table 3 for b=0.25, and shown in Figs. 28-31 for b=0.25 and b=1.

The quantity L_j is rather insensitive to the value of $b \equiv B/B_{\rm min}$ for the current sample, and thus is insensitive to offsets from minimum energy conditions. The reason is that the dependence of v on b just about cancels the dependence of P on b. When $B \equiv bB_{\rm min} \geq B_{MB}$ , as is the case here, Eq. (1) indicates that $v \propto b^{1.5}$ , and for $b \leq 1$ , which is expected to be the case, $P \propto b^{-1.5}$ , so $L_j \propto vP$ is quite insensitive to the value of b. Thus, the values of L_j obtained here remain valid even if the relativistic plasma in the sources is not close to minimum energy.

The values of L_j range from about 10⁴⁴ to 10⁴⁶ erg/s or so. There is no dependence of L_j on core-hotspot separation, as indicated in Tables 4 and 5, suggesting that the beam power of a particular source is roughly constant over the lifetime of that source. There is a correlation between beam power and redshift, as is expected from the fact that the parent population is a subset of the flux limited 3CR sample.

3.4 Ambient gas densities

The equation of ram pressure confinement (e.g., De Young 2002) indicates that the ambient gas density is given by $n_{\rm a} \propto P/v^2$ , with the constant of proportionality equal to $1/(1.4~\mu m_{\rm p})$ , where $\mu$ is the mean molecular weight of the gas taken to be 0.63 for solar abundances, and $m_{\rm p}$ is the proton rest mass. It is well known that the ambient gas density obtained with this equation for b=1 is well below that known to be present from X-ray observations. This is the primary reason to consider values of b less than one. The studies of Carilli et al. (1991) of Cygnus A and Perley & Taylor (1991) of 3C 295 indicate that b is likely to be less than one. The study of WDW suggests that the dispersion of b for very powerful classical double radio galaxies like those included in this study is less than about 15%.

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f32.ps} \end{figure}$	Figure 32: Ambient density $n_{\rm a}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f33.ps} \end{figure}$	Figure 33: Ambient density $n_{\rm a}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f34.ps} \end{figure}$	Figure 34: Ambient density $n_{\rm a}$ as a function of redshift (1+z) for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f35.ps} \end{figure}$	Figure 35: Ambient density $n_{\rm a}$ as a function of redshift (1+z) for b=0.25.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f36.ps} \end{figure}$	Figure 36: Source lifetime $T_{\rm T}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f37.ps} \end{figure}$	Figure 37: Source lifetime $T_{\rm T}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f38.ps} \end{figure}$	Figure 38: Source lifetime $T_{\rm T}$ as a function of redshift (1 + z) for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f39.ps} \end{figure}$	Figure 39: Source lifetime $T_{\rm T}$ as a function of redshift (1 + z) for b=0.25.
Open with DEXTER

The ambient gas density in the vicinity of the hotspot was determined for each side of each source for the 11 new radio galaxies for b = 0.25 and for b = 1, following the procedure of WDW, and combined with the previously determined values of the ambient gas density for the other 20 sources. The results are shown in Figs. 32-35 as a function of core-hotspot distance and redshift, and listed in Table 3 for b = 0.25.

The ambient gas density falls with distance from the source center, as indicated in Tables 5 and 6. For b = 0.25, $n_a \propto r^{-1.9 \pm 0.6}$ ; the uncertainty of 0.6 is estimated by correcting the best fit uncertainty of 0.2 by $\sqrt{(\chi^2/58)}$ , since there are 60 data points or 58 degrees of freedom included in the fit. For b = 1, $n_a \propto r^{-1.38 \pm 0.28}$ with the uncertainty corrected from the raw value of 0.13 by $\sqrt{(\chi^2/58)}$ . The magnitude of the ambient gas density is similar to that in cluster-type gaseous environments for b = 0.25, and well below that for b=1. The values of the ambient gas density and offsets from minimum energy conditions obtained and studied here are consistent with recent X-ray studies (Belsole et al. 2007; Croston et al. 2007).

3.5 Total outflow lifetimes

The total outflow lifetime $T_{\rm T}$ is an estimate of the total lifetime of the jet (past and future) that is powering that side of the source in its current cycle of radio activity. It is obtained from the beam power using the relationship, $T_{\rm T} \propto L_j^{-\beta/3}$ for the best fit value of $\beta = 1.5$ obtained by Daly et al. (2009), and it is normalized using Cygnus A. $T_{\rm T}$ is not the current synchrotron or dynamical age of the source, but is the total time that the outflow will be supplying beam power to the source hot spots. The empirical basis for the relationship and its derivation are described in detail by Daly et al. (2009). The total lifetime is interesting because the total energy that will be channeled through the jet over its lifetime can be obtained from using the relation $E_* = L_jT_{\rm T}$ .

The total lifetime of the jet on each side of each source is shown in Figs. 36-39 for b=1 and b=0.25; although the beam power is nearly independent of b, the normalization does depend upon this parameter. We see that the total lifetime determined in this way does not depend on the distance of the hotspot from the core of the source, indicating that we are randomly sampling the source during its lifetime, and the estimated total lifetime does not depend on the age of the source at the instant it is observed. The source lifetime does depend on redshift, as expected from the dependence of beam power on redshift. This follows from the fact that the sample is flux limited, so we only observe the most powerful sources at high redshift; these are the sources with large beam power and correspondingly small total lifetimes.

The estimated total lifetimes are roughly a few $\times$ 10⁶ yr for b=1 and are about a factor of 5 higher for b=0.25. This is the lifetime of the radio luminous outflow. However, there is a correlation between optical emission line luminosity and radio luminosity in powerful radio galaxies (e.g., Baum & Heckman 1989; Rawlings & Saunders 1991; Xu et al. 1999; Willott et al. 1999). This requires the radio outflow phase to be accompanied by an optically luminous QSO phase which can ionize the emission line nebulae. Thus, in these powerful radio galaxies, the QSO phase must persist for at least the lifetime of the radio source giving an independent lower limit to the QSO lifetime of a few $\times$ 10⁶ to a few $\times$ 10⁷ yr (depending on the value of b). This has implications for the question of how much mass is accreted by the black hole during a bright phase (e.g., Martini 2004).

3.6 Total outflow energy

The total outflow energy $E_{\rm T}$ is an estimate of the total energy that the jet will deposit into the radio source over the entire lifetime of the jet $T_{\rm T}$ , and is obtained using the expression $E_{\rm T} = L_j T_{\rm T}$ . The total outflow energies (E/c²) are a few $\times$ $10^5~M_\odot$ for b=1 and about a factor of 5 higher for b=0.25.

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f40.ps} \end{figure}$	Figure 40: Source total energy $E_{\rm T}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f41.ps} \end{figure}$	Figure 41: Source total energy $E_{\rm T}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f42.ps} \end{figure}$	Figure 42: Source total energy $E_{\rm T}$ as a function of redshift (1 + z) for b=1.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f43.ps} \end{figure}$	Figure 43: Source total energy $E_{\rm T}$ as a function of redshift (1 + z) for b=0.25.
Open with DEXTER

The total energy that will be processed by the central engine and expelled through the jet during the entire lifetime of the jet is shown in Figs. 40-43 for two values of b. The total energy is independent of core-hotspot separation (see Tables 5 and 6), indicating that we are observing the source at a random epoch during the lifetime of the source and our estimate of total outflow energy does not depend on the actual age of the source when we observe it. The total energy does depend upon redshift as expected from the dependence of beam power on redshift and the fact that $E_{\rm T} \propto L_j^{0.5}$ ; this is an artifact of the fact that we are working with a flux limited sample.

4 Summary

We present an analysis of new multi-wavelength VLA observations of eleven very powerful classical double radio galaxies with redshifts between 0.4 and 1.3. We estimate spectral ages and velocities for each radio bridge. Pressures and widths for each side of each source are also determined. These quantities are used to solve for the beam power, ambient gas density, total source lifetime, and total energy channeled through the jets over the source lifetime both assuming minimum energy conditions, and allowing for an offset from these conditions.

Results obtained with the eleven new sources were combined with a sample of 20 radio galaxies, and the characteristics of the full sample of 31 sources were studied. The velocities are independent of core-hotspot separation, suggesting that the velocity of a given source is roughly constant over that source lifetime. The velocities are independent of redshift, suggesting that there are no redshift-dependent systematic effects/errors in the computation of the velocity. Our result that source expansion speeds are roughly constant is consistent with independent studies based on the statistics of powerful radio galaxies, theoretical modeling, and numerical simulations.

Typical beam powers are in the range from 10⁴⁴ to 10⁴⁶ erg/s, and this quantity is insensitive to offsets from minimum energy conditions due to the fact that $L_j \propto v~P$ , and $v \propto b^{1.5}$ and $P \propto b^{-1.5}$ for $b \leq 1$ , and $B \geq B_{MB}$ , which is the range of magnetic field strengths relevant for these sources. We find that the beam powers are independent of core-hotspot separation, suggesting that the beam power of a given source is roughly constant over that source lifetime.

The estimated total lifetimes are roughly a few $\times$ 10⁶ yr for b = 1(equipartition), and about 5 times higher for b=0.25. The observed correlation between radio luminosity and optical emission line luminosity requires the radio source to be accompanied by an optically bright QSO phase. Thus, the total source lifetimes derived here are lower limits on the QSO phase of the activity.

The total outflow energies (E/c²) are a few $\times$ $10^5~M_\odot$ for b=1 (equipartition) and about a factor of 5 higher for b=0.25.

Typical ambient gas densities are similar to those in clusters of galaxies at the current epoch for an offset from minimum energy conditions by a factor of about 0.25. The ambient gas densities (obtained from the ram pressure confinement of the forward region of the source) decrease as the core-hotspot distance increases, as expected for source sizes of about 30 to 400 kpc, but have no redshift dependence.

Acknowledgements

We would like to thank the referee for helpful comments and suggestions. We would like to acknowledge helpful conversations with Roger Blandford, Greg Taylor, Paul Wiita, Dan Harris, and Alan Marscher. We are grateful to the Penn State University Computer Center for the use of their IMSL libraries. Support for this work was provided in part by US National Science Foundation grant number AST-0507465 (R. A. D.). This research made use of (1) the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration; and (2) NASA's Astrophysics Data System Abstract Service.

Appendix A: Comparison of methods for determining spectral ages

In Sects. 2.2 and 3.1 we determined the spectral age and velocity using a two position measurement of the spectral index gradient. Here, we consider the velocity of the source obtained at multiple locations on each side of each source, and find results that are very similar and consistent with those obtained in Sect. 3.1.

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416fA1.ps} \end{figure}$	Figure A.1: v/c as a function of core to hot spot distance for b=1. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 4.0 $\pm$ 1.0 $\times$ 10^-4 with $\chi ^2 = 929$ consistent with the results obtained using method A (Table 6).
Open with DEXTER

$\begin{figure} \includegraphics[width=8cm,clip]{9416fA2.ps} \end{figure}$	Figure A.2: v/c as a function of core to hot spot distance for b=0.25. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 1.3 $\pm$ 0.2 $\times$ 10^-4 with $\chi ^2 = 972$ consistent with the results obtained using method A (Table 5).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416fA3.ps} \end{figure}$	Figure A.3: v/c as a function of redshift for b=1. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 0.11 $\pm$ 0.03 with $\chi ^2 = 957$ consistent with the results obtained using method A (Table 6).
Open with DEXTER

$\begin{figure} \includegraphics[width=8cm,clip]{9416fA4.ps} \end{figure}$	Figure A.4: v/c as a function of redshift for b=0.25. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 0.022 $\pm$ 0.0045 with $\chi ^2 = 1109$ consistent with the results obtained from the two position method (Table 5).
Open with DEXTER

To obtain the velocity at several different locations across the source, we determine the spectral index at intervals of 2.5 arcsec (roughly one CLEAN beam FWHM) from the hot spot along the brightness ridge of the lobe. At each position we determine the break frequency by comparing the observed spectral index with the calculations of the JP model using the Myers and Spangler method. The one sigma range of the spectral index was used to obtain the uncertainty of the break frequency. The age of the electrons at that location is obtained using Eq. (1), and the age and distance from the hot spot are combined to obtain the rate of growth of the source (the expansion velocity); the source, angular separation of each interval from the hot spot, break frequencies at zero redshift, and source velocities are listed in (Table A.1). The average rate of growth of each side is obtained using the weighted mean expansion velocity for each lobe, and is also listed. Positions near the hot spot (where there is little spectral aging) have high and uncertain break frequencies. The weighted average velocities for each lobe are consistent with those we determined using the two position method. Figures A.1-A.4 show the average velocity as a function of core to hot spot distance and redshift including the velocities derived from the multiple position method. The results are in very good agreement with our results from the two position method, which is easily seen by comparing Figs. 1-4 with Figs. A.1-A.4. The agreement between the two methods is about 1 sigma. If the two velocity determinations are compared without accounting for the uncertainty of each velocity, the scatter between the two methods is about 24%.

To view the comparison between the two determinations of the rate of growth of the sources, we can consider fits to the 11 new radio galaxies only. There are no discernible differences between fits to v(r) or v(1+z) for b=1 and b=0.25 using method A, which is that described in the main text, and method B, which is described here. Generally, the $\chi^2$ of the fits is very large, so it is appropriate to multiple the error of the best fit parameters by $\sqrt{(\chi^2/58)}$ , as described earlier. For b=1, the slope of $v_{\rm B}(r) ~{\rm is}~ 0.0005$ $\pm$ 0.0005, while the slope of $v_{\rm A}(r) ~$ is $~ 0.0009 \pm 0.0002$ , both of which indicate either no or a very weak dependence of v with D and which are consistent at about one sigma; we also find that the slope of $v_{\rm B}(1+z)~$ is 0.1 $\pm$ 0.3, while the slope of $v_{\rm A}(1+z) ~$ is 0.1 $\pm$ 0.3, which are consistent and neither of which indicates a significant trend. Here and throughout the units of distance r are kpc and the velocity v is relative to the speed of light. For b=0.25, the slope of $v_{\rm B}(r) ~$ is 0.0001 $\pm$ 0.0001, while the slope of $v_{\rm A}(r) ~$ is 0.0003 $\pm$ 0.00003, which are consistent at a few sigma and neither of which indicates a strong trend; we also find the slope of $v_{\rm B}(1+z)~$ is 0.05 $\pm$ 0.05 and the slope of $v_{\rm A}(1+z) ~$ is 0.06 $\pm$ 0.06, both of which are consistent with zero slope and with each other.

Table A.1: Estimates of velocities at multiple positions in the lobes in the eleven radio galaxies.

In addition, we can compare the slopes of the fits to the full samples with the velocities of the eleven new sources determined using method A and method B. For b=1, the slope of $v_{\rm B}(r) ~$ is 0.0004 $\pm$ 0.0004, while the slope of $v_{\rm A}(r)$ is 0.0007 $\pm$ 0.0004, both of which indicate no dependence of v with D; we also find that the slope of $v_{\rm B}(1+z)~$ is 0.1 $\pm$ 0.1, while the slope of $v_{\rm A}(1+z) ~$ is 0.1 $\pm$ 0.1, which are consistent at the one sigma level and neither of which indicates a significant trend. For b=0.25, the slope of $v_{\rm B}(r) ~$ is 0.0001 $\pm$ 0.0001, while the slope of $v_{\rm A}(r)$ is 0.0001 $\pm$ 0.0001, which are consistent at better than one sigma and neither of which indicates a strong trend; we also find the slope of $v_{\rm B}(1+z)~$ is 0.02 $\pm$ 0.02 and the slope of $v_{\rm A}(1+z)$ is 0.02 $\pm$ 0.015, both of which are consistent with zero slope and with each other. Again, the slopes are determined with v in units of c and r in units of kpc.

Clearly, results obtained with method A and method B are very similar.

References

Alexander, P. 1987, MNRAS, 225, 27 [NASA ADS] (In the text)
Alexander, P. 2000, MNRAS, 319, 8 [NASA ADS] [CrossRef] (In the text)
Alexander, P., & Leahy, J. P. 1987, MNRAS, 225, 1 [NASA ADS] (In the text)
Appl, S., Sol, H., & Vicente, L. 1996, A&A, 310, 419 [NASA ADS] (In the text)
Barthel, P. D. 1989, ApJ, 336, 606 [NASA ADS] [CrossRef] (In the text)
Baum, S. A., & Heckman, T. 1989, ApJ, 336, 702 [NASA ADS] [CrossRef] (In the text)
Begelman, M. C. 1996, in Cygnus A - Study of a Radio Galaxy, ed. C. Carilli, & D. Harris (Cambridge: Cambridge University Press), 209 (In the text)
Begelman, M. C., & Cioffi, D. F. 1989, ApJ, 345, L21 [NASA ADS] [CrossRef] (In the text)
Black, A. R. S., Baum, S. A., Leahy, J. P., et al. 1992, MNRAS, 256, 186 [NASA ADS] (In the text)
Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 [NASA ADS] (In the text)
Belsole, E., Worrall, D. M., Hardcastle, M. J., & Croston, J. H. 2007, MNRAS, 381, 1109 [NASA ADS] [CrossRef] (In the text)
Blundell, K. M., Rawlings, S., & Willott, C. J. 1999, AJ, 117, 677 [CrossRef] (In the text)
Bridle, A. H., & Perley, R. A. 1984, ARA&A, 22, 319 [NASA ADS] [CrossRef] (In the text)
Burch, S. F. 1977, MNRAS, 180, 623 [NASA ADS] (In the text)
Carilli, C. L., Perley, R. A., Dreher, J. W., & Leahy, J. P. 1991, ApJ, 383, 554 [NASA ADS] [CrossRef] (In the text)
Carvalho, J., & O'Dea, C. P. 2002a, ApJS, 141, 337 [NASA ADS] [CrossRef] (In the text)
Carvalho, J., & O'Dea, C. P. 2002b, ApJS, 141, 371 [NASA ADS] [CrossRef]
Crane, P. C., & Napier, P. J. 1985, in Synthesis Imaging, ed. R. A. Perley, F. R. Schwab, & A. H. Bridle, NRAO, Charlottesville, 87 (In the text)
Croston, J. H., Hardcastle, M. J., Harris, D. E., et al. 2005, ApJ, 626, 733 [NASA ADS] [CrossRef]
Daly, R. A. 1990, ApJ, 355, 416 [NASA ADS] [CrossRef] (In the text)
Daly, R. A. 2002, NewAR., 46, 47 [NASA ADS] [CrossRef] (In the text)
Daly, R. A., Mory, M. P., O'Dea, C. P., et al. 2009, ApJ, 691, accepted [arXiv:0710.51125] (In the text)
De Young, D. S. 1997, ApJ, 490, L55 [NASA ADS] [CrossRef] (In the text)
De Young, D. S. 2002, The Physics of Extragalactic Radio Sources (Chicago: University of Chicago Press) (In the text)
Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [NASA ADS] (In the text)
Fanti, C., Fanti, R., Dallacasa, D., et al. 1995, A&A, 302, 317 [NASA ADS] (In the text)
Garrington, S. T., Leahy, J. P., Conway, R. G., & Laing, R. A. 1988, Nature, 331, 147 [NASA ADS] [CrossRef] (In the text)
Guerra, E. J., Daly, R. A., & Wan, L. 2000, ApJ, 544, 659 [NASA ADS] [CrossRef] (In the text)
Hardcastle, M. J., & Looney, L. J. 2008, MNRAS, in press [arXiv:0804.3369] (In the text)
Hardcastle, M. J., Croston, J. H., & Kraft, R. P. 2007, ApJ, 669, 893 [NASA ADS] [CrossRef] (In the text)
Jaffe, W. J., & Perola, G. C. 1973, A&AS, 26, 423 [NASA ADS] (In the text)
Jamrozy, M., Konar, C., Machalski, J., & Saikia, D. J. 2008, MNRAS, 385, 1286 [NASA ADS] [CrossRef] (In the text)
Kaiser, C. R. 2000, A&A, 362, 447 [NASA ADS] (In the text)
Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] (In the text)
Kaiser, C. R., Dennett-Thorpe, J., & Alexander, P. 1997, MNRAS, 292, 723 [NASA ADS] (In the text)
Kapahi, V. K., & Saikia, D. J. 1982, JApA, 3, 465 [NASA ADS] (In the text)
Kardashev, N. S. 1962, Soviet Astr.-AJ, 6, 317 [NASA ADS] (In the text)
Kharb, P., & Shastri, P. 2004, A&A, 425, 825 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Kharb, P., O'Dea, C. P., Baum, S. A., et al. 2008, ApJS, 174, 74 [NASA ADS] [CrossRef] (In the text)
Laing, R. A. 1988, Nature, 331, 149 [NASA ADS] [CrossRef] (In the text)
Leahy, J. P. 1991, in Beams and Jets in Astrophysics, ed. P. A. Hughes (Cambridge: Cambridge University Press) (In the text)
Leahy, J. P., & Williams, A. G. 1984, MNRAS, 210, 929 [NASA ADS] (In the text)
Leahy, J. P., Muxlow, T. W. B., & Stephens, P. W. 1989, MNRAS, 239, 401 [NASA ADS] (In the text)
Liu, R., Pooley, G., & Riley, J. M. 1992, MNRAS, 257, 545 [NASA ADS] (In the text)
Longair, M. S., & Riley, J. M. 1979, MNRAS, 188, 625 [NASA ADS] (In the text)
Mack, K.-H., Klein, U., O'Dea, C. P., Willis, A. G., & Saripalli, L. 1998, A&A, 329, 431 [NASA ADS] (In the text)
Machalski, J., Chyzy, K. T., Stawarz, L., & Koziel, D. 2007, A&A, 462, 43 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Martini, P. 2004, in Coevolution of Black Holes and Galaxies (Cambridge: Cambridge University Press), ed. P. Ho, 169 (In the text)
Meyers, S. T., & Spangler, S. R. 1985, ApJ, 291, 52 [NASA ADS] [CrossRef] (In the text)
Miley, G. K. 1980, ARA&A, 18, 165 [NASA ADS] [CrossRef] (In the text)
Murgia, M. 2003, PASA, 20, 19 [NASA ADS] (In the text)
Murgia, M., Fanti, C., Fanti, R., et al. 1999, A&A, 345, 769 (In the text)
Nagai, H., Inoue, M., Asada, K., Kameno, S., & Doi, A. 2006, ApJ, 648, 148 [NASA ADS] [CrossRef] (In the text)
Neeser, M. J., Eales, S. A., Law-Green, J., et al. 1995, ApJ, 451, 76 [NASA ADS] [CrossRef] (In the text)
O'Dea, C. P., & Baum, S. A. 1997, AJ, 113, 148 [CrossRef] (In the text)
Orienti, M., Dallacasa, D., & Stanghellini, C. 2007, A&A, 461, 923 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
Orr, M. J. L., & Browne, I. W. A. 1982, MNRAS, 200, 1067 [NASA ADS] (In the text)
Pacholczyk, A. G. 1970, Radio Astrophysics (San Francisco: Freeman) (In the text)
Parma, P., Murgia, M., Morganti, R., et al. 1999, A&A, 344, 7
Perley, R. A. 1985, in Synthesis Imaging, ed. R. A. Perley, F. R. Schwab, & A. H. Bridle, NRAO, Charlottesville, 161 (In the text)
Perley, R. A., & Taylor, G. B. 1991, AJ, 101, 1623 [NASA ADS] [CrossRef] (In the text)
Polatidis, A. G., & Conway, J. E. 2003, PASA, 20, 69 [NASA ADS] (In the text)
Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] (In the text)
Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] (In the text)
Snellen, I. A. G., Schilizzi, R. T., Miley, G. K., et al. 2000, MNRAS, 319, 445 [NASA ADS] [CrossRef] (In the text)
Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [CrossRef] (In the text)
Wan, L., & Daly, R. A. 1998, ApJ, 499, 614 [NASA ADS] [CrossRef] (In the text)
Wan, L., Daly, R. A., & Guerra, E. J. 2000, ApJ, 544, 671 [NASA ADS] [CrossRef] (In the text)
Wellman, G. F., Daly, R. A., & Wan, L. 1997, ApJ, 480, 96 [NASA ADS] [CrossRef] (WDW) (In the text)
Willott, C., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [NASA ADS] [CrossRef] (In the text)
Xu, C., Livio, M., & Baum, S. A. 1999, AJ, 118, 1169 [CrossRef] (In the text)

Online Material

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f01.ps} \end{figure}$	Figure 1: 3C 6.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.20 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f02.ps} \end{figure}$	Figure 2: 3C 6.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.20 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f03.ps} \end{figure}$	Figure 3: 3C 34 east hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.33 $\times$ 0.26 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f04.ps} \end{figure}$	Figure 4: 3C 34 west hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.33 $\times$ 0.26 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f05.ps} \end{figure}$	Figure 5: 3C 41 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.21 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f06.ps} \end{figure}$	Figure 6: 3C 41 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.21 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f07.ps} \end{figure}$	Figure 7: 3C 44 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f08.ps} \end{figure}$	Figure 8: 3C 44 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f09.ps} \end{figure}$	Figure 9: 3C 54 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f10.ps} \end{figure}$	Figure 10: 3C 54 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f11.ps} \end{figure}$	Figure 11: 3C 114 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f12.ps} \end{figure}$	Figure 12: 3C 114 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f13.ps} \end{figure}$	Figure 13: 3C 142.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f14.ps} \end{figure}$	Figure 14: 3C 142.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f15.ps} \end{figure}$	Figure 15: 3C 169.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f16.ps} \end{figure}$	Figure 16: 3C 172 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.26 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f17.ps} \end{figure}$	Figure 17: 3C 172 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.26 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f18.ps} \end{figure}$	Figure 18: 3C 441 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.22 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f19.ps} \end{figure}$	Figure 19: 3C 441 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.22 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f20.ps} \end{figure}$	Figure 20: 3C 469.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.32 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f21.ps} \end{figure}$	Figure 21: 3C 469.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.32 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER

Footnotes

... galaxies: Figures 1-21 are only available in electronic form at http://www.aanda.org

All Tables

Table 1: Comparison of hot spot spectral indices.

Table 2: Estimates of ages of the eleven radio galaxies.

Table 3: Summary of source properties.

Table 4: Summary of source properties. II.

Table 5: Fits to the data (b = 0.25).

Table 6: Fits to the data (b = 1).

Table A.1: Estimates of velocities at multiple positions in the lobes in the eleven radio galaxies.

All Figures

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f22.ps} \end{figure}$	Figure 22: Source advance velocity v/c as a function of core-hotspot distance r for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f23.ps} \end{figure}$	Figure 23: Source advance velocity v/c as a function of core-hotspot distance r for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f24.ps} \end{figure}$	Figure 24: Source advance velocity v/c as a function of redshift (1+z) for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f25.ps} \end{figure}$	Figure 25: Source advance velocity v/c as a function of redshift (1+z) for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f26.ps} \end{figure}$	Figure 26: Pressure in the lobe P measured at 10 h^-1 kpc from the hotspot toward the central region of the source, as a function of core-hotspot distance r for b = 0.25. The pressure for b=1 is lower by a factor of 0.218 since P(b=1) = 0.218 P(b=0.25).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f27.ps} \end{figure}$	Figure 27: Pressure in the lobe P measured at 10 h^-1 kpc from the hotspot toward the central region of the source, as a function of (1 + z) for b = 0.25. The pressure for b=1 is lower by a factor of 0.218 since P(b=1) = 0.218 P(b=0.25).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f28.ps} \end{figure}$	Figure 28: Beam power L_j as a function of core-hotspot distance r for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f29.ps} \end{figure}$	Figure 29: Beam power L_j as a function of core-hotspot distance r for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f30.ps} \end{figure}$	Figure 30: Beam power L_j as a function of redshift (1+z) for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f31.ps} \end{figure}$	Figure 31: Beam power L_j as a function of redshift (1+z) for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f32.ps} \end{figure}$	Figure 32: Ambient density $n_{\rm a}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f33.ps} \end{figure}$	Figure 33: Ambient density $n_{\rm a}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f34.ps} \end{figure}$	Figure 34: Ambient density $n_{\rm a}$ as a function of redshift (1+z) for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f35.ps} \end{figure}$	Figure 35: Ambient density $n_{\rm a}$ as a function of redshift (1+z) for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f36.ps} \end{figure}$	Figure 36: Source lifetime $T_{\rm T}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f37.ps} \end{figure}$	Figure 37: Source lifetime $T_{\rm T}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f38.ps} \end{figure}$	Figure 38: Source lifetime $T_{\rm T}$ as a function of redshift (1 + z) for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f39.ps} \end{figure}$	Figure 39: Source lifetime $T_{\rm T}$ as a function of redshift (1 + z) for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f40.ps} \end{figure}$	Figure 40: Source total energy $E_{\rm T}$ as a function of core-hotspot distance r for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f41.ps} \end{figure}$	Figure 41: Source total energy $E_{\rm T}$ as a function of core-hotspot distance r for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f42.ps} \end{figure}$	Figure 42: Source total energy $E_{\rm T}$ as a function of redshift (1 + z) for b=1.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f43.ps} \end{figure}$	Figure 43: Source total energy $E_{\rm T}$ as a function of redshift (1 + z) for b=0.25.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416fA1.ps} \end{figure}$	Figure A.1: v/c as a function of core to hot spot distance for b=1. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 4.0 $\pm$ 1.0 $\times$ 10^-4 with $\chi ^2 = 929$ consistent with the results obtained using method A (Table 6).
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=8cm,clip]{9416fA2.ps} \end{figure}$	Figure A.2: v/c as a function of core to hot spot distance for b=0.25. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 1.3 $\pm$ 0.2 $\times$ 10^-4 with $\chi ^2 = 972$ consistent with the results obtained using method A (Table 5).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416fA3.ps} \end{figure}$	Figure A.3: v/c as a function of redshift for b=1. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 0.11 $\pm$ 0.03 with $\chi ^2 = 957$ consistent with the results obtained using method A (Table 6).
Open with DEXTER
In the text

$\begin{figure} \includegraphics[width=8cm,clip]{9416fA4.ps} \end{figure}$	Figure A.4: v/c as a function of redshift for b=0.25. For the new sample of eleven radio galaxies we use the weighted average velocities from Table A.1. The slope is 0.022 $\pm$ 0.0045 with $\chi ^2 = 1109$ consistent with the results obtained from the two position method (Table 5).
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f01.ps} \end{figure}$	Figure 1: 3C 6.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.20 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f02.ps} \end{figure}$	Figure 2: 3C 6.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.20 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f03.ps} \end{figure}$	Figure 3: 3C 34 east hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.33 $\times$ 0.26 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f04.ps} \end{figure}$	Figure 4: 3C 34 west hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.33 $\times$ 0.26 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f05.ps} \end{figure}$	Figure 5: 3C 41 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.21 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f06.ps} \end{figure}$	Figure 6: 3C 41 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.21 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f07.ps} \end{figure}$	Figure 7: 3C 44 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f08.ps} \end{figure}$	Figure 8: 3C 44 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f09.ps} \end{figure}$	Figure 9: 3C 54 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f10.ps} \end{figure}$	Figure 10: 3C 54 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f11.ps} \end{figure}$	Figure 11: 3C 114 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f12.ps} \end{figure}$	Figure 12: 3C 114 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.22 $\times$ 0.21 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f13.ps} \end{figure}$	Figure 13: 3C 142.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f14.ps} \end{figure}$	Figure 14: 3C 142.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.0 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f15.ps} \end{figure}$	Figure 15: 3C 169.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.24 $\times$ 0.19 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f16.ps} \end{figure}$	Figure 16: 3C 172 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.26 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f17.ps} \end{figure}$	Figure 17: 3C 172 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.26 $\times$ 0.23 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f18.ps} \end{figure}$	Figure 18: 3C 441 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.22 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f19.ps} \end{figure}$	Figure 19: 3C 441 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.23 $\times$ 0.22 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f20.ps} \end{figure}$	Figure 20: 3C 469.1 north hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.32 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

$\begin{figure} \par\includegraphics[width=8cm,clip]{9416f21.ps} \end{figure}$	Figure 21: 3C 469.1 south hot spot. 8.4 GHz VLA image from Kharb et al. (2008) with CLEAN restoring beam FWHM 0.32 $\times$ 0.18 arcsec (shown in the inset in the lower left). Two circles are shown centered on the brightness peak. The larger circle has a diameter of 2.5 arcsec, while the smaller circle has a diameter of 1.0 arcsec.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.