| Issue |
A&A
Volume 494, Number 2, February I 2009
|
|
|---|---|---|
| Page(s) | 489 - 508 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361:200809372 | |
| Published online | 22 December 2008 | |
Kinematic modeling of disk galaxies
III. The warped ``Spindle'' NGC 2685
G. I. G. Józsa1 - T. A. Oosterloo1,2 - R. Morganti1,2 - U. Klein3 - T. Erben3
1 - Netherlands Institute for Radio Astronomy (ASTRON), Postbus 2, 7990 AA Dwingeloo, The Netherlands
2 - Kapteyn Astronomical Institute, Univ. Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
3 - Argelander-Institut für Astronomie (AIfA), Univ. Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
Received 9 January 2008 / Accepted 10 October 2008
Abstract
This is the third of a series of papers in which the structure and
kinematics of disk galaxies is studied. By employing direct tilted-ring
fits to the data cube as introduced in Paper I, we analyzed
the ``Spindle'' galaxy NGC 2685, previously
regarded as a two-ringed polar ring galaxy.
Deep H I and optical (
![]() -band) observations are
presented. The H I observations strongly suggest that the
gaseous structure of NGC 2685 does not consist of two separate
mutually inclined regions, but forms a coherent, extremely warped
disk, the appearance of two rings being due to projection effects. By
comparing the H I total-intensity maps with the optical image,
we demonstrate that at large radii a faint stellar disk is well
aligned with the outer H I disk. The shape of the dust lanes
obscuring the NE part of the inner stellar body indicates that, also at
smaller radii, NGC 2685 possesses a disk containing gas, dust, and
stars in which the various constituents are aligned.
-band) observations are
presented. The H I observations strongly suggest that the
gaseous structure of NGC 2685 does not consist of two separate
mutually inclined regions, but forms a coherent, extremely warped
disk, the appearance of two rings being due to projection effects. By
comparing the H I total-intensity maps with the optical image,
we demonstrate that at large radii a faint stellar disk is well
aligned with the outer H I disk. The shape of the dust lanes
obscuring the NE part of the inner stellar body indicates that, also at
smaller radii, NGC 2685 possesses a disk containing gas, dust, and
stars in which the various constituents are aligned.
At smaller radii, this disk is kinematically decoupled from the
central stellar body; hence, in the region of the bright, central
stellar body, NGC 2685 appears to consist of two disks that share a
common center, but have different orientation: a bright stellar
lenticular body apparently devoid of dust and gas, and a heavily
warped low-surface brightness disk containing stars, gas, and dust. The
low-surface-brightness disk changes its orientation gradually and at
large radii assumes the orientation of the central stellar S0
disk. Since, according to our analysis, the intrinsic orientation of
the low-surface-brightness disk changes through
![]() ,
the gaseous
disk is coherent, and is at no radius oriented perpendicularly with
respect to the central stellar body, NGC 2685 is not likely to be a
classical polar-ring galaxy.
,
the gaseous
disk is coherent, and is at no radius oriented perpendicularly with
respect to the central stellar body, NGC 2685 is not likely to be a
classical polar-ring galaxy.
Key words: galaxies: kinematics and dynamics - galaxies: structure - galaxies: ISM - galaxies: peculiar - galaxies: individual: NGC 2685
1 Introduction
NGC 2685 obtained the name ``Spindle Galaxy'' from Sandage (1961) who referred to this object as ``perhaps the most unusual galaxy in the Shapely-Ames catalog''. The image consists of a bright central object elongated from NE to SW. The whole of the NE side of the central object is obscured by dust lanes with associated star-forming regions. Dust lanes and H II regions are missing on the SW side. In projection, the dust lanes resemble a helical structure, hence NGC 2685 is also often referred to as the ``Helix''. At larger radii an outer stellar ring is visible on optical images that appears to have the same orientation as the central object. Basic properties of NGC 2685 are listed in Table 1 where distance-dependent quantities taken from the literature were corrected for differences in the assumed distances (see Sect. 5).
An inner ionized gas component, rotating rapidly on orbits
perpendicular to the major axis of the central stellar object, was
detected by Ulrich (1975). She showed that, inside radii of
![]() to
to
![]() ,
this component is rotating differentially
with a projected amplitude of about
,
this component is rotating differentially
with a projected amplitude of about
![]() .
This was confirmed by Schechter & Gunn (1978), who analyzed
stellar absorption - and emission spectra employing long-slit
observations along the projected major - and minor axes of the central
body. For the stellar component they found a velocity gradient along
the major axis. They observed that the central galaxy shows
non-solid-body rotation with a projected amplitude of
.
This was confirmed by Schechter & Gunn (1978), who analyzed
stellar absorption - and emission spectra employing long-slit
observations along the projected major - and minor axes of the central
body. For the stellar component they found a velocity gradient along
the major axis. They observed that the central galaxy shows
non-solid-body rotation with a projected amplitude of
![]() and concluded that it is a lenticular galaxy
(see also Whitmore et al. 1990; Emsellem et al. 2004). Whitmore et al. (1990)
showed that the inner ring structure has an excess luminosity with
respect to the central body, indicating the existence of a stellar
component in the inner ring and the helical structure. As a result,
NGC 2685 is claimed to be a polar-ring galaxy with a gaseous- and
stellar component that rotates at rather small radii on a polar orbit
about a central lenticular galaxy.
and concluded that it is a lenticular galaxy
(see also Whitmore et al. 1990; Emsellem et al. 2004). Whitmore et al. (1990)
showed that the inner ring structure has an excess luminosity with
respect to the central body, indicating the existence of a stellar
component in the inner ring and the helical structure. As a result,
NGC 2685 is claimed to be a polar-ring galaxy with a gaseous- and
stellar component that rotates at rather small radii on a polar orbit
about a central lenticular galaxy.
Table 1: Basic properties of NGC 2685.
Today's picture of NGC 2685 as containing two kinematically
independent, clearly separated kinematic systems in the neutral gas
was drawn by Shane (1980,1977) and sustained in
other studies by Mahon (1992) and
Schinnerer & Scoville (2002). Examining H I synthesis observations
of the galaxy, they conclude that the neutral gas resides in two
separate rings. One is supposedly connected with the dust lane
structure seen in the galaxy. The other one at large radii is assumed
to be oriented perpendicularly with respect to the first ring. It
seems to be aligned with the central stellar body and to rotate at a
speed of about
![]() .
.
The purpose of this paper is to present new observations conducted with the westerbork synthesis radio relescope (WSRT, Westerbork, The Netherlands) and the 2.5 m Isaac Newton Telescope (INT, Roque de los Muchachos, Spain). Using our H I observations to perform a simple tilted-ring analysis, we argue that the picture of NGC 2685 containing two separate H I rings is probably not tenable: we reproduce the H I observations by assuming a coherent, warped disk structure of the H I component, in which the orbits are circular. Comparing our model to the observations, there is no evidence of significant deviations from circular orbits, except possibly at the edges of the projected central body. Based on these findings we suggest a different scenario. In addition to the central stellar body NGC 2685, contains an extremely warped disk of low surface brightness, consisting of gas, dust, and stars. Only in projection the galaxy does appear to have two rings and a central ``helix''. At large radii the gaseous disk shares its orientation with the central lenticular galaxy. Since the single low-surface brightness disk is coherent and changing its orientation gradually, NGC 2685 does not contain two clearly separated systems with nearly orthogonal spin vectors. This means that NGC 2685 is probably not a classic polar ring galaxy as defined by Whitmore et al. (1990). (A polar ring galaxy contains two rotating sub-systems, a disk and a ring or an additional disk, of comparable sizes with orthogonal angular momentum vectors of similar amplitude; both systems share the center and the systemic velocity and the ring is nearly planar). The rotation curve derived from the H I data resembles a rotation curve of a spiral galaxy, staying relatively flat out to the last measured data point. The shape of rotation curve, in conjunction with the extreme warp geometry, indicates that the overall potential is not extremely flattened but close to spherical.
Table 2: Summary of observations and data reduction.
The paper is laid out as follows. In Sect. 2 our observations and the data reduction are described. In Sect. 3 we compare the appearance of NGC 2685 in the optical and in the H I. In Sect. 4 we present basic arguments in favor of NGC 2685 possessing one coherent, warped disk, rather than two separate disks. In Sect. 5 the data analysis via a direct tilted-ring modeling is described, the results of which are discussed in Sect. 6. In Sect. 7 the possible presence and location of non-circular motions is discussed. In Sect. 8 we briefly discuss dynamical implications of our kinematical model. Section 9 discusses the detection of possible companions to NGC 2685. Section 10 summarizes our results and a discusses possible formation scenarios for the peculiar structure of NGC 2685. Supplementary figures and tables are placed in the appendix.
2 Observations and data reduction
2.1 Optical observations
NGC 2685 was observed with the INT in the ![]() -band from
February 26 until March 4, 2004 under non-photometric weather
conditions. Each night, sky flats and bias frames were obtained.
Using a series of exposures with a maximum of 400 s single exposure
time while using a wide dithering scheme the total on-source observing
time amounts to 13 350 s. To obtain a coadded image from the
data we made use of the GaBoDS Wide Field Imager reduction pipeline
(Schirmer et al. 2003; Erben et al. 2005). After the overscan- and bias
correction, the images of each chip were flat-fielded,
super-flat-fielded and defringed on a per-night basis. Non-Gaussian
noise-features (cosmic rays, hotand cold pixels) were detected and
masked, and the single frames visually inspected to apply a
manual masking or, in some cases, to reject single frames. The images
were photometrically (relatively) calibrated,
background-subtracted and co-added, taking into account the sky
background variation in the single chips and solving for astrometric
distortion and for the relative sensitivity of the chips by making use
of the USNO-A2 standard catalog (Monet 1998). Using average
zero-points for the WFC, as published in the Internet by the CASU INT
Wide Field Survey team (McMahon et al. 2001) the resulting unbinned
coadded map can roughly be estimated to have a noise level of
-band from
February 26 until March 4, 2004 under non-photometric weather
conditions. Each night, sky flats and bias frames were obtained.
Using a series of exposures with a maximum of 400 s single exposure
time while using a wide dithering scheme the total on-source observing
time amounts to 13 350 s. To obtain a coadded image from the
data we made use of the GaBoDS Wide Field Imager reduction pipeline
(Schirmer et al. 2003; Erben et al. 2005). After the overscan- and bias
correction, the images of each chip were flat-fielded,
super-flat-fielded and defringed on a per-night basis. Non-Gaussian
noise-features (cosmic rays, hotand cold pixels) were detected and
masked, and the single frames visually inspected to apply a
manual masking or, in some cases, to reject single frames. The images
were photometrically (relatively) calibrated,
background-subtracted and co-added, taking into account the sky
background variation in the single chips and solving for astrometric
distortion and for the relative sensitivity of the chips by making use
of the USNO-A2 standard catalog (Monet 1998). Using average
zero-points for the WFC, as published in the Internet by the CASU INT
Wide Field Survey team (McMahon et al. 2001) the resulting unbinned
coadded map can roughly be estimated to have a noise level of
![]() (see Table 2. The
obtained image is shown in Fig. 1 (upper left panel).
(see Table 2. The
obtained image is shown in Fig. 1 (upper left panel).
2.2 H I observations
NGC 2685 was observed with the WSRT in December 2002 (
![]() h)
and January 2004 (
h)
and January 2004 (![]() h, see Table 2). To ensure
good central UV-coverage all observations were done in maxi-short
configuration. We used a total bandwidth of
h, see Table 2). To ensure
good central UV-coverage all observations were done in maxi-short
configuration. We used a total bandwidth of
![]() ,
two
parallel polarizations, and 1024 channels in total. The data
underwent a standard data reduction with the Miriad
(Sault et al. 1995) software package (for a detailed description see
Józsa 2006). The continuum data resulting from a second-order
continuum subtraction with the Miriad-task uvlin were used to correct
the frequency-independent gains by means of self-calibration. To
enhance the signal-to-noise ratio, we performed a second continuum
subtraction on the self-calibrated data. We used the clean table of
our continuum image to subtract a continuum model from the
visibilities (Miriad task uvmodel). Then, we performed a first-order
continuum subtraction using 550 line-free channels (Miriad task
uvlin). Before inverting the visibilities we applied a Hanning
smoothing using the miriad task uvfil. Two data cubes, a
high-resolution (uniform weighting using all baselines) and a
low-resolution one (Robust weighting of 0.4, using baselines of length
<6.4
,
two
parallel polarizations, and 1024 channels in total. The data
underwent a standard data reduction with the Miriad
(Sault et al. 1995) software package (for a detailed description see
Józsa 2006). The continuum data resulting from a second-order
continuum subtraction with the Miriad-task uvlin were used to correct
the frequency-independent gains by means of self-calibration. To
enhance the signal-to-noise ratio, we performed a second continuum
subtraction on the self-calibrated data. We used the clean table of
our continuum image to subtract a continuum model from the
visibilities (Miriad task uvmodel). Then, we performed a first-order
continuum subtraction using 550 line-free channels (Miriad task
uvlin). Before inverting the visibilities we applied a Hanning
smoothing using the miriad task uvfil. Two data cubes, a
high-resolution (uniform weighting using all baselines) and a
low-resolution one (Robust weighting of 0.4, using baselines of length
<6.4
![]() ), were produced. The data cubes were deconvolved
using an iterative CLEAN with appropriate masks. The derived total
flux for NGC 2685 is in good agreement with single-dish measurements
(Richter et al. 1994), showing that no substantial fraction of the
flux is resolved out in the H I observations. Representative
examples of resulting channel maps are shown in Figs. A.1 and A.2. Total intensity maps and first-moment maps were
generated by first masking the cubes with the finally applied clean
masks. The resulting high-resolution total-intensity map, the
low-resolution total-intensity map, and a low-resolution moment-1 map
are shown in Fig. 1. A second plot of the high-resolution
total intensity map and the corresponding velocity field are shown in A.3.
), were produced. The data cubes were deconvolved
using an iterative CLEAN with appropriate masks. The derived total
flux for NGC 2685 is in good agreement with single-dish measurements
(Richter et al. 1994), showing that no substantial fraction of the
flux is resolved out in the H I observations. Representative
examples of resulting channel maps are shown in Figs. A.1 and A.2. Total intensity maps and first-moment maps were
generated by first masking the cubes with the finally applied clean
masks. The resulting high-resolution total-intensity map, the
low-resolution total-intensity map, and a low-resolution moment-1 map
are shown in Fig. 1. A second plot of the high-resolution
total intensity map and the corresponding velocity field are shown in A.3.
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8.8cm]{9372_01a.eps}\i...
...72_01c.eps}\includegraphics[angle=270,width=8.8cm]{9372_01d.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg125.gif) |
Figure 1:
Top, left panel: logarithmic grey-scale plot of the i'-band image obtained with the INT. Top, right panel: grey-scale plot of the high-resolution H I total-intensity map. Bottom, left panel: low-resolution total-intensity H I map (contours and grey scale). Contours represent the
|
| Open with DEXTER | |
3 The relation between stars and ISM in NGC 2685
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{9372_02a.eps}\includegraphi...
...idth=6cm]{9372_02d.eps}\includegraphics[width=6cm]{9372_02f.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg134.gif) |
Figure 2: Parametrizations of toy model data cubes and toy model total-intensity maps. Top panels: ``Flip model''. The orientation of the disk flips at a certain radius, the minimum requirement for speaking of a two-ring or two-disk system in NGC 2685. Bottom panels: ``Warp model''. Here a coherent but heavily warped disk is assumed. Left: surface brightness profile, rotation curve and disk orientation. SD: H I face-on column density/surface mass density. VROT: rotation velocity. INCL: inclination. PA: position angle. R: radius. Middle: three-dimensional visualizations of the disks. Right: toy model total-intensity maps. The lines trace the track along which the spectra in the position-velocity diagrams (PV-diagrams) shown in Fig. 3 are traced. |
| Open with DEXTER | |
The upper left panel in Fig. 1 shows the optical image of the Spindle obtained with the INT WFC, while in the top right panel a grey-scale plot of the H I high-resolution, total-intensity map is shown, using the same spatial scale. A comparison by eye is sufficient to identify several structures to be present in all maps.
Firstly, apart from showing the central lenticular body, the optical image resembles the integrated H I map in such close detail that there is little doubt that both stars and gas belong to the same structure that exists in addition to the central stellar body. Especially the small deviations from axisymmetry, such as a hook-like structure to the NE side of the galaxy and a more diffuse structure towards the SW side, are visible in all images (see also Shane 1980,1977).
Secondly, there is no region completely devoid of stars or gas within the projected outer ring. Thanks to the high sensitivity of our observations, this is also evident in the high-resolution H I map (Fig. 1, top right panel), where beam-smearing effects can be excluded as causing the appearance of a filled inner region. This means that the galaxy possesses an extended disk or, being a rather implausible option, a stellar and gaseous halo that does not belong to its inner bright lenticular stellar body.
Thirdly, looking at the high-resolution H I map (Fig. 1, top right panel), it seems that the helical structure is also present in the H I component. Apparently, the H I follows the dust lane structure like H I follows spiral arms in spiral galaxies. As the H I component is optically thin, the spiral-arm structures can be seen on both sides of the galaxy. Using integral-field emission line spectra from the SAURON survey (Emsellem et al. 2004) and the H I data presented here, Morganti et al. (2006) show that the neutral gas has an ionized counterpart towards the center (see also Ulrich 1975) of the galaxy and that the ionized gas shares the kinematical structure of the H I in the overlap region.
It can be concluded that the H I component in the galaxy belongs to one or two structures, distinct from the central stellar body, which contain molecular, neutral, and ionized gas, dust, and stars. The distribution of all components follows the H I distribution. At the largest radii beyond the outer projected ring, the H I maps show a disk-like extension that cannot be seen in the optical image, possibly due to insufficient sensitivity in the optical observations. The outer disk is not detected in the observations of Shane (1980) but is evident in the work of Mahon (1992) and Schinnerer & Scoville (2002).
4 The warped structure of the gas disk of NGC 2685
It has been argued that the H I component of NGC 2685 consists of two rings (Shane 1980; Schinnerer & Scoville 2002; Shane 1977; Mahon 1992). For a number of reasons, we believe that this is probably not the case.
The spectral and integrated appearance of the H I
component
Our main point is that the total H i appearance and the kinematics as observed in the H I component of NGC 2685 are not well matched with two disjunct rings or disks.
To demonstrate this, we constructed two tilted-ring models using our software TiRiFiC (Józsa et al. 2007, hereafter Paper I). These represent a galaxy as a set of thin, mutually inclined rings projected on a data cube. The model parametrizations and 3-d realizations of the toy models are shown in Fig. 2. For the first toy model (``flip model'') it is assumed that the H I disk of NGC 2685 flips at a certain radius. The other model (``warp model''), has a smooth transition from one disk orientation to the next. Figure 2 displays the total-intensity maps of the two models. Both models were kept as simple as possible, while a rough match with the observations was achieved by changing the model parameters by hand. Both models require an H I deficiency towards the center to reproduce the central H I ``hole''. Comparing to the original total-intensity map (Fig. 1), the shape of the outer ring and the intensity distribution along the ring is clearly represented better by the warp model. While an elliptical ring is produced in the flip model, the shape of the outer ring is properly reproduced and deviates from a perfect ellipse in the warp model. This is only due to projection effects. The intensity maxima on the minor axis of the ring are highly concentrated at the position where the two disks adjoin in the flip model, while in the warp model they are smoothed out along the outer ring as is the case in the observed total-intensity map. The diffuse appearance of the projected surface brightness at the major axis positions is also seen in the warp model, while it is not in the flip model.
The strongest argument against a sudden flip in the H I disk of NGC 2685 concerns the kinematics. Figure 3 shows position-velocity diagrams (PV-diagrams) along the lines shown in Fig. 2 calculated from the original low-resolution data cube and the two toy model data cubes. Any discontinuity in the disk orientation causes a gap between the spectral features that belong to the single constituents, as is the case for the flip model. There is no connecting feature to be seen between the intensity maxima belonging to the ``outer ring'' (intensity peaks closer to the systemic velocity) and the intensity maxima belonging to the ``inner ring''. The PV-diagrams taken from the original data cube and from the warp model show this connection. The superior quality of our observations, in this case the high spectral resolution, enables us to ensure that the connection of the intensity peaks in the PV-diagram of the original data is a real feature and not due to resolution effects.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270]{9372_03a.eps}}...
...}\\
\resizebox{8cm}{!}{\includegraphics[angle=270]{9372_03c.eps}}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg135.gif) |
Figure 3: PV-diagrams along the lines across the minor axis of the inner ring shown in Fig. 2. Top panel: taken from the flip model data cube. Middle panel: taken from the original data cube. Bottom panel: taken from the warp-model data cube. The ellipses in the lower left corners denote the clean beam major axis ( HPBW) and the velocity resolution ( FWHM). The warp model is able to reproduce the connecting feature indicated by the ellipses, while the flip model is not. |
| Open with DEXTER | |
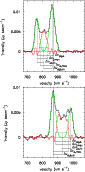 |
Figure 4:
Spectra taken from the low-resolution data cube at the positions indicated by the boxes in Fig. 1. Black: the original spectrum. Light grey (green in online version): fitted Gaussians. Dark grey (red in online version): residual after subtracting the fitted
Gaussians from the original profile. The velocity differences
|
| Open with DEXTER | |
Under the assumption of the presence of two kinematically disjunct
rings, strong streaming motions have to be invoked to give rise to the
connecting feature (Fig. 3). We analyzed 18 spectra at
equidistant positions on either side of the center of the galaxy. They
were chosen to show the connecting feature in the PV-diagram of
Fig. 3. The spectra were taken from our low-resolution data
cube, at the positions of
![]() adjacent pixels indicated by
boxes in Fig. 1. The co-ordinates of the corresponding
positions are listed in Table B.1 in the
appendix.
adjacent pixels indicated by
boxes in Fig. 1. The co-ordinates of the corresponding
positions are listed in Table B.1 in the
appendix.
Figure 4 shows two example spectra, extracted at
the center of the boxes. Like the example spectra, all spectra show
the same features, two intensity peaks are visible, connected at a
lower intensity level. Under the assumption that two separate rings
are observed in NGC 2685, the positions of the peak closer to the
systemic velocity mark the line-of-sight velocity of the outer ring
and the other peak positions mark the line-of-sight velocity of the inner
ring. If all emission would stem from gas on regular orbits, one
expects the shape of both emission features to resemble a
Gaussian. The rotation velocity of NGC 2685 at a distance of
![]() from the center is already comparable to the overall
rotational amplitude of the galaxy
(Ulrich 1975; Shane 1980). Inside that radius NGC 2685 is devoid of
H I. Thus, the assumption is justified.
from the center is already comparable to the overall
rotational amplitude of the galaxy
(Ulrich 1975; Shane 1980). Inside that radius NGC 2685 is devoid of
H I. Thus, the assumption is justified.
In the two-ringed
picture, gas at intermediate velocities belongs to one of the rings,
but does not follow the regular orbits of the inner or the outer
ring. To separate the anomalous gas component from the regular gas
component, we fitted two Gaussians to the peaks, and subtracted them
from the spectra (Fig. 4). From the peak positions of the
fitted Gaussians and the velocities at 20 percent of the peak
intensity level of the residuum, we calculated the projected bulk- and
maximal excess velocities of the anomalous component with respect to
the assumed regular components (see Fig. 4). We also
calculated the total flux contained in the residuum and in the fitted
components (see Table B.1 in the appendix). On average, if
the excess component belonged to the outer ring, our analysis
would indicate a bulk excess velocity of the anomalous component of
![]() ,
reaching on average
,
reaching on average
![]() .
If it belonged to the inner ring, the average bulk
excess velocity would amount to
.
If it belonged to the inner ring, the average bulk
excess velocity would amount to
![]() ,
reaching on average
,
reaching on average
![]() .
The mass of the
anomalous component compared to the mass contained in the outer ring
averages to
.
The mass of the
anomalous component compared to the mass contained in the outer ring
averages to
![]() .
Compared to the mass contained in the inner ring it is on average
.
Compared to the mass contained in the inner ring it is on average
![]() .
The
projected velocities of the assumed excess component reach
more than two thirds of the assumed projected rotation velocity of
either ring and are on average at a level of nearly half the assumed
rotation velocity (for the inner ring we assumed
.
The
projected velocities of the assumed excess component reach
more than two thirds of the assumed projected rotation velocity of
either ring and are on average at a level of nearly half the assumed
rotation velocity (for the inner ring we assumed
![]() as the projected rotation velocity, for the inner ring we directly
determined
as the projected rotation velocity, for the inner ring we directly
determined
![]() from the spectra, see
Fig. 4).
from the spectra, see
Fig. 4).
We thus conclude that the hypothesis that the H I in NGC 2685 has the structure of two disconnected rings or disks would require the presence of massive streaming motions to explain the spectral appearance of the H I. This would, however, contradict the lack of enhanced star formation in the galaxy (Schinnerer & Scoville 2002). Hence, an analysis of our spectral data cube renders this hypothesis improbable. We also note that it would state a strong coincidence to detect gas with such strong deviations from the regular component at the junction of the projected rings. This would not contradict the two-ring hypothesis but weakens it even further. The assumption of a strongly warped H I disk qualitatively fits the observations. We thus conclude that the (spectral) appearance of NGC 2685 is most compatible with the assumption that it is caused by geometrical effects. In the following Sect. 5 we show that we can reproduce the data cube in great detail under that assumption.
For the ionized gas disk of NGC 2685, the warped structure of the helix has already been documented by Nicholson et al. (1987). Further support for the warp hypothesis comes from optical measurements, mainly showing that the H I structure is also found to be present in stars and dust (see also Sect. 3).
The dust lanes
The appearance of the dust lanes obscuring the whole NE part of the
central body is inconsistent with a single central ring. The simplest
way to explain the shape of the dust lanes would be to assume a strong
warp in the associated component. This has already been done by other
authors (e.g. Taniguchi et al. 1990; Simonson & Tohline 1983; Nicholson et al. 1987) and agrees
with our suggestion that the inner low-surface brightness
component of NGC 2685 is a heavily warped disk.
The outer disk and the filled inner ring
Beyond the outer apparent H I-ring, NGC 2685 possesses a
diffuse, extended structure, most likely a disk (since it shows a
rotational signature in the velocity field, Fig. 1). The
outer disk has already been detected by Mahon (1992). As
mentioned above, another feature directly evident in the H I maps is that no empty regions are found inside the outer apparent
H I-ring (Sect. 3). This is especially true for the
optical image and the high-resolution H I total-intensity
map (Fig. 1, upper right panel). Both have sufficient
resolution and sensitivity to detect such holes. If the central
H I structure was a polar ring, we have to assume in our flip
model a filled inner region of low-surface brightness, oriented like
the outer ring, leading to a quite implausible surface-brightness
profile in the flip model (Fig. 2, top left). While it has
been suggested that the outer projected ring could be a resonance
feature reacting to the central stellar body, which would then be a
bar-like structure (Schinnerer & Scoville 2002), the stellar velocity
field published by Emsellem et al. (2004) leaves little doubt that
the central stellar body is a differentially rotating disk as has
already been found by Schechter & Gunn (1978). Under the assumption of
a polar ring, the same very peculiar surface brightness profile in the
gas and in the stars would be required to fill the area
inside the projected outer ring. When a warp is assumed this is not the
case. As shown in Fig. 2 (bottom left panel), the required schematic surface brightness profile resembles that of a normal disk galaxy.
The arguments given above make it plausible to draw the following picture: NGC 2685 contains a stellar- and gaseous disk that shares typical characteristics with the disks of spiral galaxies. However, the disk is extremely warped and NGC 2685 owes its two-ringed appearance to projection effects. Apparently, the helical structure consists of dust-features made up of spiral arms that are wrapped around the central body in a warped structure.
Cases of extreme warps are not unknown. Schwarz (1985)
quantified the structure of the warp in the large spiral galaxy
NGC 3718. It shows an extreme warp in its stellar and gaseous disk
that changes its orientation by nearly
![]() .
In this galaxy, which
has a different orientation and does not appear ring-like in
projection, the warp is already evident through the appearance of
dust lanes in optical photographs. In a similar approach to the one presented above, Arnaboldi & Galletta (1993) showed that the galaxy NGC 660 probably
has a very simple disk structure with a large-amplitude warp.
Several cases of extremely warped H I disks in gas-rich early
type galaxies are known
(Sparke et al. 2008; Morganti et al. 1997; Oosterloo et al. 2002; Serra et al. 2006; Oosterloo et al. 2007),
suggesting that warps of large amplitude could be a common feature
among this type of galaxy. Also, the kinematical decoupling of the
inner stellar- and gaseous components is not an uncommon feature for
early-type galaxies (Sarzi et al. 2006).
.
In this galaxy, which
has a different orientation and does not appear ring-like in
projection, the warp is already evident through the appearance of
dust lanes in optical photographs. In a similar approach to the one presented above, Arnaboldi & Galletta (1993) showed that the galaxy NGC 660 probably
has a very simple disk structure with a large-amplitude warp.
Several cases of extremely warped H I disks in gas-rich early
type galaxies are known
(Sparke et al. 2008; Morganti et al. 1997; Oosterloo et al. 2002; Serra et al. 2006; Oosterloo et al. 2007),
suggesting that warps of large amplitude could be a common feature
among this type of galaxy. Also, the kinematical decoupling of the
inner stellar- and gaseous components is not an uncommon feature for
early-type galaxies (Sarzi et al. 2006).
5 Tilted-ring modeling
After having argued that there are reasons to believe that the
H I (-and optical) disk of NGC 2685 is heavily warped, we
present our attempts to fit a full tilted-ring model to the data
cube. Due to the assumed warp, the projections of the orbits are very
crowded at some positions. It is impossible to disentangle this orbit
crowding employing any tilted-ring analysis of a velocity field (see
discussion in Paper I). Instead, we perform a direct, automated fit to
the data cube with our software TiRiFiC. Since the software is
described in detail in Papers I and II (Józsa 2007; Józsa et al. 2007), we refer to these papers and to Józsa (2006) for the details of the analysis procedure. The low-resolution data cube was analyzed first using a spacing of ring radii of
![]() .
The center of the galaxy, the systemic
velocity, the velocity dispersion, and the scale height were kept as
free parameters, but were not allowed to vary independently from ring
to ring. For each ring, the surface-brightness, the orientational
parameters, and the rotation velocity were varied independently. To
estimate errors, independent fits to the receding and approaching side
were performed. The errors were calculated as the maximum deviation
of the parameters from the fits to the approaching and the receding
side from the earlier fit to the entire galaxy. The errors of the
central position, scale height, the systemic velocity and the global
dispersion of the galaxy can be very roughly estimated to be less than
.
The center of the galaxy, the systemic
velocity, the velocity dispersion, and the scale height were kept as
free parameters, but were not allowed to vary independently from ring
to ring. For each ring, the surface-brightness, the orientational
parameters, and the rotation velocity were varied independently. To
estimate errors, independent fits to the receding and approaching side
were performed. The errors were calculated as the maximum deviation
of the parameters from the fits to the approaching and the receding
side from the earlier fit to the entire galaxy. The errors of the
central position, scale height, the systemic velocity and the global
dispersion of the galaxy can be very roughly estimated to be less than
![]() and
and
![]() ,
respectively, roughly
corresponding to half the (minor-axis) FWHM of the resolution for the
high-resolution data cube (concerning the accuracy of the applied
method see Paper I). In a few cases, where the errors calculated were
obviously too large or too small, the data were visually inspected and
errors were estimated by varying the parameter in question and
comparing the resulting model data cubes with the original data cube. This
was only necessary for some data points at the largest and the
smallest radii. To refine the spatial resolution in the inner regions
of the galaxy, the high-resolution data cube was used. Up to a radius
of
,
respectively, roughly
corresponding to half the (minor-axis) FWHM of the resolution for the
high-resolution data cube (concerning the accuracy of the applied
method see Paper I). In a few cases, where the errors calculated were
obviously too large or too small, the data were visually inspected and
errors were estimated by varying the parameter in question and
comparing the resulting model data cubes with the original data cube. This
was only necessary for some data points at the largest and the
smallest radii. To refine the spatial resolution in the inner regions
of the galaxy, the high-resolution data cube was used. Up to a radius
of
![]() ,
where all parameters vary rapidly with radius, the
spacing of the ring radii was refined to
,
where all parameters vary rapidly with radius, the
spacing of the ring radii was refined to
![]() .
The finally
resulting fit is shown in Fig. 6. Figure 5
illustrates the geometry of the fitted disk by means of an
``inclinogram'', projecting the rings onto the celestial plane.
By analyzing the high-resolution data cube, it was found that the
H I surface brightness inside a radius of
.
The finally
resulting fit is shown in Fig. 6. Figure 5
illustrates the geometry of the fitted disk by means of an
``inclinogram'', projecting the rings onto the celestial plane.
By analyzing the high-resolution data cube, it was found that the
H I surface brightness inside a radius of
![]() -
-
![]() was negligibly small. Therefore, the
orientational parameters are not constrained at the origin. We
consider our model and the formal errors reliable beyond the third
data point (at a radius of
was negligibly small. Therefore, the
orientational parameters are not constrained at the origin. We
consider our model and the formal errors reliable beyond the third
data point (at a radius of
![]() ). Figure A.1
in the appendix shows contour-plots overlaying the low-resolution data
cube with the corresponding synthetic data cube.
). Figure A.1
in the appendix shows contour-plots overlaying the low-resolution data
cube with the corresponding synthetic data cube.
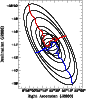 |
Figure 5:
``Inclinogram'' of the NGC 2685 overlaid on the original total intensity maps: the ellipses mark the projection of the rings at radii of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=18cm]{9372_06.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg160.gif) |
Figure 6: Tilted-ring parametrization of the Spindle galaxy. SBR: surface brightness (upper limits only for the first two data points). VROT: rotation velocity. INCL: inclination (unconstrained at origin). PA: position angle (unconstrained at origin). R: radius. The vertical line denotes the optical radius r25. |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8.5cm]{9372_07a.eps} \...
...2_07c.eps} \includegraphics[angle=270,width=8.5cm]{9372_07d.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg163.gif) |
Figure 7:
Top panels: total-intensity contour plots ( left panel) and first-moment velocity fields ( right panel) derived from the low-resolution data cubes (dark-grey, blue in online version: original, light grey, pink in online version: model) overlaid on a
total-intensity grey-scale map derived from the observed data cube. The ellipse in the lower left corner represents the clean beam. The contours represent the
|
| Open with DEXTER | |
To estimate some of the global physical parameters shown in
Table 1, the Tully-Fisher relation was applied to derive the
distance of NGC 2685 following Sakai et al. (2000, Sak00), treating the
galaxy like a spiral galaxy.
We used Eq. (11) in Sak00 to estimate the total
extinction-corrected I-band magnitude of the galaxy. To correct for
inclination, the H I 50% line width was derived by changing
all modeled inclinations to
![]() and determining a line width of
and determining a line width of
![]() by artificially observing NGC 2685
as if observing an edge-on disk. The apparent I-band magnitude of
by artificially observing NGC 2685
as if observing an edge-on disk. The apparent I-band magnitude of
![]() (see Table 1) was taken from
Prugniel & Heraudeau (1998) as listed in Paturel et al. (2003). A (marginal)
k-correction was applied and the magnitude was corrected for Galactic
(0
(see Table 1) was taken from
Prugniel & Heraudeau (1998) as listed in Paturel et al. (2003). A (marginal)
k-correction was applied and the magnitude was corrected for Galactic
(0
![]() 121, NED, following Schlegel et al. 1998) and internal
extinction. For the latter, we use a 20%-linewidth of
121, NED, following Schlegel et al. 1998) and internal
extinction. For the latter, we use a 20%-linewidth of
![]() (not corrected for inclination), derived from our
model data cube, which compares well to the
(not corrected for inclination), derived from our
model data cube, which compares well to the
![]() published by van Driel et al. (Table 2, from Richter et al. 1994, Table 1), and the logarithmic axis ratio
published by van Driel et al. (Table 2, from Richter et al. 1994, Table 1), and the logarithmic axis ratio
![]() (LEDA, Paturel et al. 2003) to apply formula 2
(Tully et al. 1998) in Sak00. This yields a Tully-Fisher distance of
(LEDA, Paturel et al. 2003) to apply formula 2
(Tully et al. 1998) in Sak00. This yields a Tully-Fisher distance of
![]() .
The large error mainly arises from the
conservative errors in the 50%-line width and the axis ratio
.
The large error mainly arises from the
conservative errors in the 50%-line width and the axis ratio
![]() that is used to estimate dust extinction. We find this
result to agree with a distance estimate using a Hubble
constant of
that is used to estimate dust extinction. We find this
result to agree with a distance estimate using a Hubble
constant of
![]() yielding
distances of
yielding
distances of
![]() (corrected for the solar motion relative to
the CMB) and
(corrected for the solar motion relative to
the CMB) and
![]() (corrected for the solar motion
relative to the Local Group) with the inherent uncertainty of the
peculiar motion of the galaxy. Therefore, we consider the use of
the Tully-Fisher relation a valid method estimating the distance to
NGC 2685.
(corrected for the solar motion
relative to the Local Group) with the inherent uncertainty of the
peculiar motion of the galaxy. Therefore, we consider the use of
the Tully-Fisher relation a valid method estimating the distance to
NGC 2685.
6 The structure of the warp
The tilted-ring model shown in Fig. 6 is visualized in
various forms in Figs. 5, 8, and 9. Our findings again support our picture drawn in Sect. 4; a sudden change in orientation, as would be
expected in case of the presence a distinct polar structure, should be
reflected in our parametrization resulting from a free fit. In
contrast, we find that the best-fit model is similar to the warp toy
model shown in Sect. 4. As is the case for the spiral
galaxy NGC 3718 (Schwarz 1985), the gaseous disk of NGC 2685
changes its orientation continuously from the innermost radii onward,
and then becomes remarkably flat towards large radii. For the
innermost
![]() -
-
![]() ,
however, no reliable information can
be derived from the data, as obviously the gas becomes ionized towards
the center of the galaxy.
,
however, no reliable information can
be derived from the data, as obviously the gas becomes ionized towards
the center of the galaxy.
Towards the center the H I disk changes its orientation
continuously. Therefore, it has a different quality from the warps
in common disks of spiral galaxies, which show an inner flat part, the
bending occurring at larger radii (Briggs 1990). It is,
however, remarkable that some typical warp features nevertheless seem
to be reproduced (for a brief review on the properties of H I
warps see Paper II). Figure 8 shows tip-LON plots
(Briggs 1990), a projection of the spin normal vectors of the
disk onto a reference plane. In the left panel this plane is
chosen to be the orbital plane at a radius of
![]() ,
the
first radius at which we consider the parametrization to be
reliable. Our analysis indicates that - in this reference frame -
quite some portion of the inner disk shares a common line-of-nodes:
with increasing radius, in the chosen projection, the LON-angle is
constant within the errors (see Fig. 8, middle panel). For
spiral galaxies the same feature is observed when choosing the flat
inner disk as a reference plane and is indicative of co-precession in
the inner warped disk (Briggs 1990). We emphasize that this
feature depends on the choice of the reference plane, since the same feature
would not be observed when choosing the orbital plane of the outer flat
disk as reference. A rapid change in the direction of the LON occurs
at a radius of
,
the
first radius at which we consider the parametrization to be
reliable. Our analysis indicates that - in this reference frame -
quite some portion of the inner disk shares a common line-of-nodes:
with increasing radius, in the chosen projection, the LON-angle is
constant within the errors (see Fig. 8, middle panel). For
spiral galaxies the same feature is observed when choosing the flat
inner disk as a reference plane and is indicative of co-precession in
the inner warped disk (Briggs 1990). We emphasize that this
feature depends on the choice of the reference plane, since the same feature
would not be observed when choosing the orbital plane of the outer flat
disk as reference. A rapid change in the direction of the LON occurs
at a radius of
![]() .
At larger radii (>120
.
At larger radii (>120
![]() ), the
data points fall into the same region, such that in the outer region
they share the same LON angle again. Consistent with observations of
normal warps, the LON advances in the direction of galactic rotation
(Briggs 1990, Paper II), indicating an outwards decreasing
torque (Shen & Sellwood 2006). The right panel in Fig. 8
illustrates that a reference plane can also be found for NGC 2685 that
divides the H I disk into two parts, connected by a small
transition region, with a comparably constant LON angle
(Briggs 1990, Paper II). The implication for warped disk
galaxies is that the disk is divided into two connected regions, each of
which is in a state of co-precession (Revaz & Pfenniger 2001). The top
panel of Fig. 9 shows the mutual inclination of the spin
vectors of the disk. Beyond a radius of
), the
data points fall into the same region, such that in the outer region
they share the same LON angle again. Consistent with observations of
normal warps, the LON advances in the direction of galactic rotation
(Briggs 1990, Paper II), indicating an outwards decreasing
torque (Shen & Sellwood 2006). The right panel in Fig. 8
illustrates that a reference plane can also be found for NGC 2685 that
divides the H I disk into two parts, connected by a small
transition region, with a comparably constant LON angle
(Briggs 1990, Paper II). The implication for warped disk
galaxies is that the disk is divided into two connected regions, each of
which is in a state of co-precession (Revaz & Pfenniger 2001). The top
panel of Fig. 9 shows the mutual inclination of the spin
vectors of the disk. Beyond a radius of
![]() ,
the values in
this diagram are consistent with being zero, meaning that NGC 2685
possesses a flat outer disk, as illustrated in an opaque 3d-model
based on our best-fit parametrization shown in the bottom panel
Fig. 9. This is also evident from the clustering of the
data points at larger radii in the tip-LON plots of Fig. 8
and the fact that the orientational parameters of the tilted-ring
parametrization (Fig. 6) do not change within the error
bars. The occurrence of the flat outer disk is a feature that has been
previously found to be present in some warped disk galaxies (Paper II
and references therein).
,
the values in
this diagram are consistent with being zero, meaning that NGC 2685
possesses a flat outer disk, as illustrated in an opaque 3d-model
based on our best-fit parametrization shown in the bottom panel
Fig. 9. This is also evident from the clustering of the
data points at larger radii in the tip-LON plots of Fig. 8
and the fact that the orientational parameters of the tilted-ring
parametrization (Fig. 6) do not change within the error
bars. The occurrence of the flat outer disk is a feature that has been
previously found to be present in some warped disk galaxies (Paper II
and references therein).
Table 3: Global best-fit tilted-ring parameters of NGC 2685.
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{9372_08a.eps}\includegraphi...
...th=5.8cm]{9372_08b.eps}\includegraphics[width=6cm]{9372_08c.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg188.gif) |
Figure 8:
Tip-LON plots for the H I disk of NGC 2685. Left and right panel: tip-LON plots (see Briggs 1990 and Paper II), the filled circles are the projection of the tip of the normal vectors of the
rings at different radii onto a reference plane; the center of the
galaxy is denoted by a larger circle. The circles are drawn at
intervals of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm]{9372_09a.eps}\par {\h...
...includegraphics[angle=270,width=5.5cm]{9372_09b.eps}\hspace*{5mm}}\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg189.gif) |
Figure 9: Top panel: ``tiltogram'' of NGC 2685. This is a pixel map showing the mutual inclination of rings at different radii (see Paper II). Bottom panel: three-dimensional model of the H I disk of NGC 2685 according to the best-fit tilted-ring model. The model is rotated and artificially made opaque to again show the presence of an outer planar disk. |
| Open with DEXTER | |
Since the warped structure of the gas disk indicates that the galaxy
is not a typical polar-ring galaxy as defined by
Whitmore et al. (1990), the question arises as to what degree a polar
orbit is reached at all in this system, either with respect to the
outer disk or with respect to the central stellar
body. Figure 8 shows that at least for radii
![]() ,
a polar orientation of outer and inner H I disk is
not compatible with our model. The outer disk, assumed to be flat, is
inclined by
,
a polar orientation of outer and inner H I disk is
not compatible with our model. The outer disk, assumed to be flat, is
inclined by
![]() with respect to the disk at a radius of
with respect to the disk at a radius of
![]() .
This is remarkably consistent with the same value found
by Sarzi et al. (2006) for the mutual inclination of the central
stellar body and ionized gas disk of NGC 2685 (see
also Nicholson et al. 1987). Our analysis speaks against the hypothesis of a true
polar structure at radii
.
This is remarkably consistent with the same value found
by Sarzi et al. (2006) for the mutual inclination of the central
stellar body and ionized gas disk of NGC 2685 (see
also Nicholson et al. 1987). Our analysis speaks against the hypothesis of a true
polar structure at radii
![]() ,
our model
becoming unreliable at smaller radii. However, the results of Sarzi et al. (2006) can be interpreted as evidence against a polar orientation in the central,
ionized part of the gaseous disk.
,
our model
becoming unreliable at smaller radii. However, the results of Sarzi et al. (2006) can be interpreted as evidence against a polar orientation in the central,
ionized part of the gaseous disk.
7 Noncircular motions
The previous sections showed that the kinematics of NGC 2685, as they appear in projection, can be represented well by the tilted-ring model. However, because of the peculiar structure of NGC 2685, the kinematics of the gas disk of the galaxy is expected to show deviations from the assumed symmetry. The orbits of any tracer material are expected to deviate from circularity. Given the lack of appropriate analysis software to deal with noncircular motions in extremely warped cases like NGC 2685, we have to restrict ourselves to a brief discussion at a phenomenological level.
Figure 10 shows the residual obtained when subtracting the
first-moment velocity maps derived from the low-resolution original-
and the model data cube for NGC 2685. In such a map, systematic
patterns indicate a mismatch of the model and the measurement. Such a
mismatch can be due to i) a wrong fit; ii) an incompatibility of
morphology and/or kinematics of the observed structure with the
assumed tilted-ring symmetry; or iii) erroneous calculation of the
weighted mean recession velocity in the noisy observed data cube. We
cannot provide any independent tests for the accuracy of our fit
method; hence, we cannot exclude the residuals in velocity arising from
a wrong fit (if they are of a first-order harmonic nature). However,
extensive tests (see Paper I) suggest that for the given geometry of
the H I disk, such errors are unlikely (for radii >1.5-2 synthetic beams) to show up in the residual velocity field.
The single obvious feature in the residual map is located at the tip
of the inner stellar body, roughly within a radial range between
![]() and
and
![]() ,
and is antisymmetric. An
interpretation can only, however, be speculative, since we use a
primitive approach as NGC 2685 is
probably
a dynamically complex
case. Using epicyclic theory, Franx et al. (1994) connect an
antisymmetric deviation from circular symmetry in the radial
velocities to a symmetric distortion in the potential, hence a bar or
an elliptic potential. However, the basic assumption made therein is
that the disk is flat, which is obviously not the case for
NGC 2685. Another straightforward suggestion would be that we
witness (vertical) precession, which would cause a first-order
harmonic distortion in radial velocity along a ring. With the
(symmetrically) warped nature of the disk, precession does not seem
unlikely. We emphasize, however, that the observed deviation of
observed and synthetic velocity field can also be caused by a purely
morphological asymmetry in the tracer material. Given the line widths
at the radii concerned (see Fig. 7), over which the
velocities are calculated as an intensity-weighted mean, this is also
a possible option. Since the feature seen is very localized, we prefer
this interpretation.
,
and is antisymmetric. An
interpretation can only, however, be speculative, since we use a
primitive approach as NGC 2685 is
probably
a dynamically complex
case. Using epicyclic theory, Franx et al. (1994) connect an
antisymmetric deviation from circular symmetry in the radial
velocities to a symmetric distortion in the potential, hence a bar or
an elliptic potential. However, the basic assumption made therein is
that the disk is flat, which is obviously not the case for
NGC 2685. Another straightforward suggestion would be that we
witness (vertical) precession, which would cause a first-order
harmonic distortion in radial velocity along a ring. With the
(symmetrically) warped nature of the disk, precession does not seem
unlikely. We emphasize, however, that the observed deviation of
observed and synthetic velocity field can also be caused by a purely
morphological asymmetry in the tracer material. Given the line widths
at the radii concerned (see Fig. 7), over which the
velocities are calculated as an intensity-weighted mean, this is also
a possible option. Since the feature seen is very localized, we prefer
this interpretation.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9372_10.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg194.gif) |
Figure 10:
Difference- or residual velocity map derived by subtracting the model first-moment map from the original first-moment map. Overlaid are the projected rings of the best-fit model at radii
|
| Open with DEXTER | |
Except for the very localized axisymmetric feature in the vicinity of the central stellar constituent, the residuals are low compared to the rotation velocity. Also the direct comparison of our model with the data (Figs. 7, A.1) shows that we reproduce the data in great detail, without obvious systematic deviations. In the presence of large deviations from the circularity of orbits, those would usually be expected to show up (Schoenmakers et al. 1997; Franx et al. 1994). Hence, in the scope of our model, we find no obvious evidence of a global deviation from the tilted-ring symmetry and, with that, of a significant global noncircularity of orbits.
Especially the suggestion that the outer projected ring could be a real accumulation of gas and stars at an outer Lindblad resonance of a bar (Schinnerer & Scoville 2002) does not fit our results. While a change of position angle and inclination in a tilted-ring model can be indicative of a bar (Schinnerer & Scoville 2002), streaming motions would leave a distinct large-scale imprint on the residual velocity field shown in Fig. 10, which is not seen (see also Erwin & Sparke 2003).
Our fitting results would certainly be improved by including an appropriate treatment of noncircular motions, like allowing for azimuthal variations of velocities along the sight (Schoenmakers et al. 1997; Franx et al. 1994). On the other hand, our simplified treatment indicates that there is probably not much room for large-amplitude harmonic terms indicative of noncircular motions, provided there is no significantly different parametrization that reproduces the data equally well. In Sect. 4, we discuss that at least a two-ringed solution seems improbable, but we are technically not able to search the complete parameter space to exclude the existence of such a solution.
8 Dynamical considerations
While polar-ring galaxies are infrequent (Whitmore et al. 1990 calculate a detection rate of roughly 0.5% among all nearby, lenticular galaxies, and estimate a fraction of 4.5% of all nearby lenticulars to have a polar ring), they are subject to quite some interest. Their kinematics contains information about the three-dimensional shape of the overall potential, since the orbits of the observed tracers (stars and gas) do not share a common plane of motion. The same accounts in principle for a galaxy with an extreme warp in a low-surface-brightness disk co-existing with a rotating, central stellar body. The main purpose of the paper is to present our observations and the consequent kinematical description of NGC 2685, while a detailed dynamical treatment under consideration of further data will follow in a different paper.
Here, we briefly discuss some implications of our tilted-ring model concerning the dynamics of the object.
8.1 The age of the low-surface brightness disk
Our analysis indicates the presence of a relaxed H I disk at
large radii, rotating regularly with a rotational period of
![]() (see Table 1). The coherence in the H I disk of
NGC 2685 suggests that its major portion has been acquired in a single
event in the evolution of NGC 2685. Due to the fact that a settling
onto regular orbits requires a few orbital periods, this implies an
age of several Gyr of the warped H I disk of NGC 2685. In line
with this is the observation that the orientation of the outer
H I (- and stellar) disk of NGC 2685 has the same orientation
as the inner lenticular stellar body, suggesting a connection of the
outer gaseous and stellar disk (Morganti et al. 2006). Following that
notion, Morganti et al. (2006) propose that the warp of the inner
low-luminosity disk formed in a later event.
(see Table 1). The coherence in the H I disk of
NGC 2685 suggests that its major portion has been acquired in a single
event in the evolution of NGC 2685. Due to the fact that a settling
onto regular orbits requires a few orbital periods, this implies an
age of several Gyr of the warped H I disk of NGC 2685. In line
with this is the observation that the orientation of the outer
H I (- and stellar) disk of NGC 2685 has the same orientation
as the inner lenticular stellar body, suggesting a connection of the
outer gaseous and stellar disk (Morganti et al. 2006). Following that
notion, Morganti et al. (2006) propose that the warp of the inner
low-luminosity disk formed in a later event.
Optical observations, however, suggest that the warp is a long-lived configuration. Peletier & Christodoulou (1993) estimated the age of the stellar population in the helical structure to lie between 2 and 5 Gyr, depending on metallicity. Following Eskridge & Pogge (1997), who found a solar abundance, the age of the stars in the helical structure is about 2 Gyr. The most recent estimates by Karataeva et al. (2004) point to a low metallicity, typical for a dIrr or an LSB galaxy, which corresponds to a larger age of the helix, possibly reaching the age of the outer disk inferred from the rotation period. A further argument for the longevity of the warped structure comes from the analysis of our model parameters, which suggest a co-precession within the helical structure, as indicated by the straight LON angle in the region of the inner warp (Sect. 6, Fig. 8); the signature of a transient warp would be a gradient in the LON angle due to a rapid wind-up through differential precession.
8.2 The kinematical model and the shape of the potential
The low-surface-brightness component in NGC 2685 tends towards a polar orientation at small radii, while at large radii the disk is aligned with the central stellar body. The age estimates for the helical structure point towards this feature being long-lived (see previous section). Without being conclusive, we discuss possibilities for explaining the warped low-surface-brightness component as a long-lived feature.
It had already been pointed out by Simonson & Tohline (1983) that NGC 2685
could contain an extremely warped component stabilized under the
influence of a prolate, tumbling potential. This was motivated by
Tohline & Durisen (1982) and van Albada et al. (1982), who found that under
the influence of such a potential, the gas would settle into a stable,
extremely warped plane. The tumbling of the potential would be
necessary to prevent the definition of two separate planes in which
orbits stable against differential precession are possible (see
e.g. Reshetnikov et al. 1994; Whitmore et al. 1990), ultimately leading to a break-up of
the warp. Since the central stellar object at that time was not
clearly identified as a ``pancake'', the alternative of an elliptical
galaxy tumbling with a rotation axis oriented towards the pole of
the outer disk could explain the shape of the warp (see also Varnas 1990; Bekki & Freeman 2002; Peletier & Christodoulou 1993). While the nature of the central
object as a lenticular galaxy has been clarified, the possibility
remains that the overall potential is nevertheless triaxial and
tumbling, which would lead to the observed structure. Consequently,
the central lenticular galaxy would be subject to the same deviation
from axisymmetry in the potential. Therefore, its kinematics should
accordingly show oval distortions. We note that such a deviation is
not reported in the literature despite the existence of
high-resolution stellar absorption line kinematics
(Emsellem et al. 2004). The absorption-line velocity-field
published by Emsellem et al. (2004) does not show any obvious signatures
of the deviations from axial symmetry indicative for an oval distortion of
the potential out to a radius of
![]() or about one third of
the region where we model the H I disk to be severely
warped. Since the potential is therefore traced in the optical on a smaller scale than the extent of the warped region,
the lack of such obvious signatures is indicative, but it does not
exclude the possibility of a tumbling, triaxial potential at larger
radii.
or about one third of
the region where we model the H I disk to be severely
warped. Since the potential is therefore traced in the optical on a smaller scale than the extent of the warped region,
the lack of such obvious signatures is indicative, but it does not
exclude the possibility of a tumbling, triaxial potential at larger
radii.
A second possibility is that the inner warped structure is stabilized via self-gravity under the influence of an oblate potential, aligned with the central stellar body. In a simplified analysis (consisting of two heavy rings, or ``wires'' under the influence of an oblate, scale-free logarithmic potential), Sparke (1986) showed that neutrally stable configurations exist, where the inner portion of a self-gravitating disk lies close to polar, while the outer disk spin axis aligns with the symmetry axis of the potential (comparable to Type II warps as defined by Sparke & Casertano 1988). However, the assumption of such a modified-tilt mode (Sparke & Casertano 1988), in which the disk would be in a state of co-precession throughout conflicts with our observations (Sect. 6, Fig. 8).
The time development of heavy disks under the influence of aspherical
potentials was investigated by Sparke (1986) (oblate) and
Arnaboldi & Sparke (1994) (prolate, figure-rotating potentials). Within
the parameter range investigated, they observed that, in case of a
large change in disk orientation (not only a slight warp), a break-up
of the disk into multiple regions occurs, which themselves show
co-precession. A global mode of co-precession is not reached. While
this is reminiscent of the rapid change in the LON angle at a radius
![]() (Fig. 8), it is questionable whether the
coherency of the disk orientation in NGC 2685 can be reproduced in a
model setup of a heavy disk in a distinctly aspherical potential. We
emphasize, however, that in the studies discussed here
(Arnaboldi & Sparke 1994; Sparke 1986; Sparke & Casertano 1988), the parameter space was not
searched to fit an extremely warped disk, since the goal was to
resemble true polar ring galaxies with slight warps in their disks or
stable modes.
(Fig. 8), it is questionable whether the
coherency of the disk orientation in NGC 2685 can be reproduced in a
model setup of a heavy disk in a distinctly aspherical potential. We
emphasize, however, that in the studies discussed here
(Arnaboldi & Sparke 1994; Sparke 1986; Sparke & Casertano 1988), the parameter space was not
searched to fit an extremely warped disk, since the goal was to
resemble true polar ring galaxies with slight warps in their disks or
stable modes.
If we assume that the low-surface brightness disk of NGC 2685 has a
negligible mass compared to the common potential of the bright S0
stellar body and the dark-matter halo, we can estimate the flattening q of the potential under the assumption of free precession in a scale-free logarithmic potential aligned with the main stellar body and
hence roughly with the outer H I disk (Morganti et al. 2006),
giving an upper limit. In the approximation of a nearly spherical,
logarithmic, scale-free potential, the disk precesses about the pole
at a precession rate given by (Sparke 1986; Cox et al. 2006)
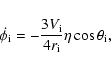 |
(1) |
where
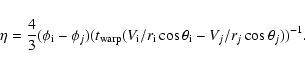 |
(2) |
We define the symmetry plane as the orbital plane given by the mean of the orientational parameters between radii of
The assumption of at most slight deviations from
sphericity of the overall potential is supported by the absence of
obvious global features in the residual velocity map
(Sect. 7). Furthermore, we find that the measured rotation
curve does not show any peculiarities compared to a rotation curve
measured for a non-warped early-type galaxy. In the case of a halo
flattening towards the polar orientation as suggested for polar ring
galaxies by Iodice et al. (2003), one would expect a distinct drop in
the measured rotation velocity within the warped region. The slight
decrease in rotation velocity towards larger radii and the shallow
maximum in a radial range of
![]() to
to
![]() is a common
feature observed for (non-warped) early type galaxies
(e.g. Noordermeer et al. 2007). The shape of the rotation curve is
therefore not indicative of a flattening of the potential.
is a common
feature observed for (non-warped) early type galaxies
(e.g. Noordermeer et al. 2007). The shape of the rotation curve is
therefore not indicative of a flattening of the potential.
In the same notion, comparing our distance estimate from the Tully-Fisher relation to the Hubble distance, we do not find a significant offset from the Tully-Fisher relation as reported by Iodice et al. (2003, NGC 2685 being a galaxy in their sample): NGC 2685 does not appear significantly dimmer than suggested by the H I line width (see Sect. 5). In a statistical treatment of several polar ring galaxies, Iodice et al. (2003) interpret such an offset from the Tully-Fisher relation as an indication of a deformation of the potential. Thus, we conclude that also the peak amplitude of the rotation curve of NGC 2685 (determining the H I line width) is not indicative of a flattening of the potential.
9 The environment of the Spindle
Table 4: Basic properties of the detected dwarf galaxies in the vicinity of NGC 2685.
In H I, NGC 2685 and four additional, small objects were detected (Fig. 11). This means that NGC 2685 is probably the dominating member of a small loose group of galaxies; hence, the question arises whether the peculiar structure of NGC 2685 might be connected to a past interaction with (one of) its companions. Two H I detections can be associated with the known dwarf galaxies UGC 4683 and PGC 25002, while two objects were detected that are barely, if at all, visible in the DSS. Their projected separation is very small ( ![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{9372_11.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg243.gif) |
Figure 11:
H I total-intensity maps of the observed field overlaid on a DSS (red) image. From top to bottom: UGC 4683, two unknown possibly
merging objects, PGC 25002, NGC 2685. The contours represent the
|
| Open with DEXTER | |
UGC 4683 has a ratio of gas mass to B-band luminosity of
![]() .
Under the assumption that the
H I in NGC 2685 comes from this galaxy, an initial ratio of gas
mass to B-band luminosity of about
.
Under the assumption that the
H I in NGC 2685 comes from this galaxy, an initial ratio of gas
mass to B-band luminosity of about
![]() before the encounter with NGC 2685 would be required. In this
case, because of the position of the galaxy with respect to NGC 2685,
UGC 4683 must have donated its gas on an orbit aligned well with the
outer gas disk, hence to the inner lenticular stellar body. Also
here it is unlikely that the complete gas content of NGC 2685 was
deposited by UGC 4683.
before the encounter with NGC 2685 would be required. In this
case, because of the position of the galaxy with respect to NGC 2685,
UGC 4683 must have donated its gas on an orbit aligned well with the
outer gas disk, hence to the inner lenticular stellar body. Also
here it is unlikely that the complete gas content of NGC 2685 was
deposited by UGC 4683.
The optical observations show a very faint elliptical stellar system located on the SW side of NGC 2685 (see Fig. 1, upper left panel). It is, however, unclear at which distance this object is with respect to NGC 2685, since it is not detected in H I. There is no evidence of any interaction as no H I feature in the gas belonging to NGC 2685 seems to be connected with the object.
We therefore conclude that the peculiar structure of NGC 2685 is probably not caused by any interaction with its direct neighbors. It is, however, clear that, with a lifetime of the helix of more than 2 Gyr, a possible donor galaxy that had an encounter with NGC 2685 can now be located at a distance of Megaparsecs. The lack of possible donors in the field-of-view of our H I observations therefore does not exclude the possibility of a gas accretion from a bypassing galaxy as a possible origin for the peculiar structure of NGC 2685.
10 Summary and discussion
We analyze deep WSRT HI synthesis observations and deep INT WFC
observations in the ![]() band of the Spindle Galaxy
NGC 2685. Our analysis includes a tilted-ring parametrization of the
H I disk. Our analysis supports the following
hypotheses:
band of the Spindle Galaxy
NGC 2685. Our analysis includes a tilted-ring parametrization of the
H I disk. Our analysis supports the following
hypotheses:
- NGC 2685 possesses two separate components, one the central S0 stellar body. The other is a coherent large-scale warped disk consisting of gas, stars, and dust. The appearance of a two-ringed structure (Shane 1980; Schinnerer & Scoville 2002; Shane 1977; Mahon 1992) stems from projection effects. This makes scenarios unlikely, in which the rings, respectively the disk, of NGC 2685 have been acquired in two separate accretion events.
- The large-scale disk shares many properties of a small spiral-galaxy disk of low surface brightness, containing molecular-, neutral-, and ionized gas and stars. The helical dust lane structure appearing in optical images can be identified with spiral arms that are matched by density peaks in the neutral gas component. The spiral arms also occur on the far side of the galaxy in high-resolution H I maps. The H I surface density profile resembles that of any spiral galaxy.
- Our analysis indicates the presence of a relaxed H I disk at large radii, rotating regularly with a rotational period of 1.3 Gyr (see Table 1). The age of the stellar population in the helical structure is between 2 and 5 Gyrs (Eskridge & Pogge 1997; Peletier & Christodoulou 1993; Karataeva et al. 2004). Since after an accretion event several rotational periods are necessary for the gas to settle on regular orbits, we conclude that the age of the gas disk is probably significantly greater than 2 Gyr. This is consistent with the findings of Karataeva et al. (2004). In contrast to Eskridge & Pogge (1997), they found a metallicity typical for a dIrr or LSB galaxy with the consequence of a higher stellar age (Peletier & Christodoulou 1993). This suggests that the large-scale disk of NGC 2685, part of which is the helical structure, has not been acquired recently, but has an intermediate age.
-
The warp in the large-scale disk shares important properties with
warps of lower amplitude in spiral galaxies. The disk is divided into
two regimes, each of which shares a common line-of-nodes
(Briggs 1990); hence, the disk is co-precessing (or not
precessing) in both regimes. The disk is coherent, so that both regimes
are connected by a small transition region. In the transition region,
the nodal line progresses in the direction of rotation, as was
previously found by Briggs (1990) for other galaxies. The outer
disk of NGC 2685 is flat out to a radius of about
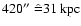 .
.
- For radii
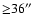 ,
where we consider our model reliable, the maximal mutual inclination of two spin vectors is
,
where we consider our model reliable, the maximal mutual inclination of two spin vectors is
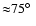 and
no polar orientation with respect to the central bright stellar body is
reached. Optical analyses indicate that this also holds for the ionized gas disk at radii
and
no polar orientation with respect to the central bright stellar body is
reached. Optical analyses indicate that this also holds for the ionized gas disk at radii
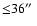 (Sarzi et al. 2006).
(Sarzi et al. 2006).
- Within the scope of our measurements and our analysis,
we do not find any obvious indications of a large deviation of the
potential from sphericity. The absence of global residuals when
subtracting the modeled velocity field from the observed ones and the
fact that the rotation curve does not show any peculiarities compared
to rotation curves of other early-type galaxies instead indicates that
the potential is close to spherical. This is consistent with an
estimate of the ellipticity of the potential in the limit of free
precession (
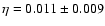 ), providing an upper limit for
the ellipticity.
), providing an upper limit for
the ellipticity.
- Because of their low H I mass compared to that of NGC 2685 and the lack of an H I-deficiency, companions of NGC 2685 detected in H I can be excluded as donors to create the entire coherent H I disk. If an interaction with a present companion galaxy created the warped structure of the large-scale disk, the interaction was mainly tidal.
As is the case for polar ring galaxies (e.g. Bekki 1997; Bournaud & Combes 2003), two scenarios come into question. The first is that NGC 2685 is the result of a merger event. Simulations of wet, dissipative mergers of spiral galaxies have shown that indeed extremely warped structures of resulting gas disks as reported here can show up as a result of a merger (Barnes 2002; Naab et al. 2006, Fig. 2 therein showing a case with a gas structure very similar to that of NGC 2685). Barnes (2002) shows that extended, regular gas disks (containing up to about half of the gas of the progenitor galaxies) can build up after a major merger that would resemble the outer H I disk of NGC 2685, while towards the center a highly inclined disk turns up, in some cases connected to the outer disk. In contrast to Naab et al. (2006), Barnes (2002) finds extremely warped gas remnants of a merger to turn up also in the case of unequal (3:1) mass mergers. This is of relevance insofar as simulations (Naab & Burkert 2003; Naab et al. 1999) show that generally equal-mass mergers tend to result in slowly rotating, boxy stellar remnants, while the central stellar body of NGC 2685, despite showing a de Vaucouleurs profile in surface-brightness (Peletier & Christodoulou 1993), is clearly a fast rotating, flattened system (Emsellem et al. 2004), as is produced in simulations with preference in unequal-mass mergers.
A second scenario could be that the central warp in NGC 2685 is the result of gas accretion, the gas being acquired either in the course of a tidal interaction with a (now distant, Sect. 9) donor galaxy (Schweizer et al. 1983; Bournaud & Combes 2003; Reshetnikov & Sotnikova 1997), or through direct infall of cold, primordial gas (Macciò et al. 2006). In the latter scenario, the (cold) accreted gas falls onto an inner part of a pre-existing spiral galaxy, is stopped in the gas disk, and mixes its angular momentum with the original gas disk only in the region of the resulting warp. Depending on the ratio of angular momentum carried by the infalling material and the disk at differing radii, in this way a warped gas structure might build up. A similar scenario has been successfully simulated by Bournaud & Combes (2003) to explain the co-existence of an inner polar and an outer equatorial ring. The difference of their model predictions and our simple model for the gas structure in NGC 2685 is that in their simulations a coherent disk and a warp of large amplitude never turns up. This occurs because within their setup the gas on an inclined orbit with respect to the progenitor disk is subject to a torque strong enough to prevent the formation of warped structure with partly low inclination with respect to the equatorial plane. Only gas on highly inclined orbits is stable against differential precession. This situation might change if the torque imposed on the mixture of infalling- and disk material is attenuated by choosing a different setup, e.g. a more dominating spherical DM halo potential.
In favor of the accretion scenario could be the excess of H I surface brightness (Fig. 6) in the region of the inner warp. The shape of the H I surface-brightness profile is not unusual compared to a spiral galaxy. One concern against the accretion scenario is the light profile of the central stellar body. Peletier & Christodoulou (1993) showed that it follows a de Vaucouleurs law, while an exponential profile would be expected if the central stellar body formed from a spiral galaxy stripped from the gas in the inner regions. Furthermore, the accretion scenario would require fine-tuning, since the structure of the gas disk of NGC 2685 is highly symmetric. An accretion event would likely also impose linear momentum on the progenitor disk, which would then probably result in a more asymmetric warp and a lopsided kinematics and gas distribution. The task would be to find a scenario where the transfer of linear momentum is small or where the resulting displacement of inner, warped disk and outer disk vanishes quickly (see e.g. Sánchez-Salcedo 2006, on the topic of warp formation through gas infall).
A possibility of distinguishing between the two tentative scenarios might be to consider photometric observations. Obviously, a stellar component has formed within the gaseous, warped disk of NGC 2685. In the merging scenario, the gas disk grows from inside out (Barnes 2002), after a rapid initial transport of gas to the center. Therefore, it is to be expected that the age of the subsequently formed stars becomes younger towards larger radii. Hence, if at all, a color gradient towards a bluer population with increasing radius is expected in the merging scenario. In the accretion scenario, since the bulk of the new star-forming material should be placed in the center of the galaxy, a transition in color from the inner, warped, region, to the outer remnant of the progenitor disk is expected to occur from bluer to redder colors. Considering the color maps published by Erwin & Sparke (2002), it is immediately evident that this distinction cannot be made easily. In fact, the inner helical structure appears reddened with respect to the outer projected ring, but this may well be due to reddening by dust and a mixing of the light from the low-surface-brightness disk and the central stellar body on the line-of-sight. According to our tilted-ring model (Fig. 5), the material along the projected outer ring is a mixture of material at both smaller and larger radii, while on the apparent minor axis it is dominated by material at smaller radii, and on the apparent major axis it is dominated by material at larger radii. Thus, one can inspect the projected ring to search for a change in color along the projected ring. While the color indeed changes along the projected outer ring, no clear trend can be made out in the color maps published by Erwin & Sparke (2002).
We cannot be conclusive about the origin of the structure of NGC 2685. However, due to the inner stellar body not following an exponential light profile, and warped gas structures do turn up in simulations of wet mergers, we give our preference to the hypothesis that NGC 2685 is the result of a merger of two disk galaxies.
NGC 2685 remains an interesting object, mainly because of the co-existence of two rotating disks of extreme symmetry at differing orientation. Exploiting the kinematics of both the stars of the central lenticular stellar body and the gas disk should lead to further insight into the 3D structure of the galaxy.
Acknowledgements
We thank the first anonymous referee for initiating the discussion about the origin of the intrinsic structure of NGC 2685 in Sect. 10 and for encouraging us to compare our results concerning the Tully Fisher relation to the work by Enrichetta Iodice and collaborators.
We would like to thank the editor, Françoise Combes, for finishing the refereeing process and for giving good advice.
The underlying Ph.D. Thesis project was partly financed by the Deutsche Forschungsgemeinschaft in the framework of the Graduiertenkolleg 787 ``Galaxy Groups as Laboratories for Baryonic and Dark Matter''.
The underlying Ph.D. Thesis project was also partly financed by the University of Bonn in the framework of the ``Research Group Bonn: Dark Matter and Dark Energy''.
G.J. would like to emphasize that the NGC 2685-project originates from his stay as summer student at ASTRON (Dwingeloo, The Netherlands).
The Westerbork Synthesis Radio Telescope is operated by the ASTRON (Netherlands Foundation for Research in Astronomy) with support from the Netherlands Foundation for Scientific Research (NWO).
The Isaac Newton Telescope is operated on the island of La Palma by the Isaac Newton Group in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.
This work makes use of a digitised image of the Second Palomar Observatory Sky Survey (POSS-II) obtained through the Digitized Sky Survey (DSS) websites. The Digitized Sky Surveys were produced at the Space Telescope Science Institute under U.S. Government grant NAG W-2166.
This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration
.
We acknowledge the use of the HyperLeda database (http://leda.univ-lyon1.fr).
Appendix A: Data cubes and moment maps
![\begin{figure}
\par\includegraphics[width=17cm,clip]{9372_A1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg258.gif) |
Figure A.1:
Selected images from the low-resolution data cube (channel width of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=17cm]{9372_A2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg261.gif) |
Figure A.2:
Selected images from the high-resolution data cube (channel width of
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=6.7cm]{9372_A3a.eps} \includegraphics[angle=270,width=6.7cm]{9372_A3b.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg263.gif) |
Figure A.3:
Total-intensity map ( left) and first-moment velocity field ( right) derive from the high-resolution data cube overlaid on a total intensity grey-scale map. The ellipse in the lower left corner represents the clean beam. The contours represent the
|
| Open with DEXTER | |
Appendix B: Results from spectral fits
Table B.1: Velocities and masses of gas detected at ``anomalous'' velocities as derived from fitting a double-Gaussian to several profiles of the data cube.
Appendix C: Tilted-ring parameters
Table C.1: Radially dependent best-fit parameters.
References
- Arnaboldi, M., & Galletta, G. 1993, A&A, 268, 411 [NASA ADS] (In the text)
- Arnaboldi, M., & Sparke, L. S. 1994, AJ, 107, 958 [NASA ADS] [CrossRef] (In the text)
- Barnes, J. E. 2002, MNRAS, 333, 481 [NASA ADS] [CrossRef]
- Bekki, K. 1997, ApJ, 490, L37 [NASA ADS] [CrossRef]
- Bekki, K., & Freeman, K. C. 2002, ApJ, 574, L21 [NASA ADS] [CrossRef]
- Bournaud, F., & Combes, F. 2003, A&A, 401, 817 [NASA ADS] [CrossRef] [EDP Sciences]
- Briggs, F. H. 1990, ApJ, 352, 15 [NASA ADS] [CrossRef] (In the text)
- Cox, A. L., Sparke, L. S., & van Moorsel, G. 2006, AJ, 131, 828 [NASA ADS] [CrossRef]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies (Berlin, Heidelberg, New York: Springer)
- Emsellem, E., Cappellari, M., Peletier, R. F., et al. 2004, MNRAS, 352, 721 [NASA ADS] [CrossRef]
- Erben, T., Schirmer, M., Dietrich, J. P., et al. 2005, Astron. Nachr., 326, 432 [NASA ADS] [CrossRef]
- Erwin, P., & Sparke, L. S. 2002, AJ, 124, 65 [NASA ADS] [CrossRef] (In the text)
- Erwin, P., & Sparke, L. S. 2003, ApJS, 146, 299 [NASA ADS] [CrossRef] (In the text)
- Eskridge, P. B., & Pogge, R. W. 1997, ApJ, 486, 259 [NASA ADS] [CrossRef] (In the text)
- Franx, M., van Gorkom, J. H., & de Zeeuw, T. 1994, ApJ, 436, 642 [NASA ADS] [CrossRef] (In the text)
- Iodice, E., Arnaboldi, M., Bournaud, F., et al. 2003, ApJ, 585, 730 [NASA ADS] [CrossRef] (In the text)
- Józsa, G. I. G. 2006, Ph.D. Thesis, Univ. Bonn, available at http://hss.ulb.uni-bonn.de/diss_online/math_nat_fak/2006/jozsa_gyula/index.htm (In the text)
- Józsa, G. I. G. 2007, A&A , 468, 903 [NASA ADS] [CrossRef] (Paper II)
- Józsa, G. I. G., Kenn, F., Klein, U., & Oosterloo, T. A. 2007, A&A, 468, 731 [NASA ADS] [CrossRef] [EDP Sciences] (Paper I) (In the text)
- Karataeva, G. M., Drozdovsky, I. O., Hagen-Thorn, V. A., et al. 2004, AJ, 127, 789 [NASA ADS] [CrossRef] (In the text)
- Macciò, A. V., Moore, B., & Stadel, J. 2006, ApJ, 636, L25 [NASA ADS] [CrossRef] (In the text)
- Mahon, M. E. 1992, BAAS, 24, 1267 [NASA ADS] (In the text)
- McMahon, R. G., Walton, N. A., Irwin, M. J., et al. 2001, New Astron. Rev., 45, 97 [NASA ADS] [CrossRef] (In the text)
- Monet, D. G. 1998, in BAAS, 30, BAAS, 1427 (In the text)
- Morganti, R., Sadler, E. M., Oosterloo, T., Pizzella, A., & Bertola, F. 1997, AJ, 113, 937 [CrossRef]
- Morganti, R., de Zeeuw, P. T., Oosterloo, T. A., et al. 2006, MNRAS, 371, 157 [NASA ADS] [CrossRef] (In the text)
- Naab, T., & Burkert, A. 2003, ApJ, 597, 893 [NASA ADS] [CrossRef]
- Naab, T., Burkert, A., & Hernquist, L. 1999, ApJ, 523, L133 [CrossRef]
- Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef]
- Nicholson, R. A., Taylor, K., Sparks, W. B., & Bland, J. 1987, in Structure and Dynamics of Elliptical Galaxies, ed. P. T. de Zeeuw, IAU Symp., 127, 415 (In the text)
- Noordermeer, E., van der Hulst, J. M., Sancisi, R., Swaters, R. S., & van Albada, T. S. 2007, MNRAS, 376, 1513 [NASA ADS] [CrossRef] (In the text)
- Oosterloo, T. A., Morganti, R., Sadler, E. M., Vergani, D., & Caldwell, N. 2002, AJ, 123, 729 [NASA ADS] [CrossRef]
- Oosterloo, T. A., Morganti, R., Sadler, E. M., van der Hulst, T., & Serra, P. 2007, A&A, 465, 787 [NASA ADS] [CrossRef] [EDP Sciences]
- Paturel, G. 1989, Catalogue of principal galaxies (PGC) (Lyon: Base de Donn�es Extragalactiques, Observatoire de Lyon)
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Peletier, R. F., & Christodoulou, D. M. 1993, AJ, 105, 1378 [NASA ADS] [CrossRef] (In the text)
- Prugniel, P., & Heraudeau, P. 1998, A&AS, 128, 299 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Reshetnikov, V., & Sotnikova, N. 1997, A&A, 325, 933
- Reshetnikov, V. P., Hagen-Thorn, V. A., & Yakovleva, V. A. 1994, A&A, 290, 693 [NASA ADS]
- Revaz, Y., & Pfenniger, D. 2001, A&A, 372, 784 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Richter, O.-G., Sackett, P. D., & Sparke, L. S. 1994, AJ, 107, 99 [NASA ADS] [CrossRef] (In the text)
- Sakai, S., Mould, J. R., Hughes, S. M. G., et al. 2000, ApJ, 529, 698 [NASA ADS] [CrossRef] (In the text)
- Sánchez-Salcedo, F. J. 2006, MNRAS, 365, 555 [NASA ADS] [CrossRef] (In the text)
- Sandage, A. 1961, The Hubble atlas of galaxies (Washington: Carnegie Institution) (In the text)
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [NASA ADS] (In the text)
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, ASP Conf. Ser., 77 (San Francisco: ASP), 433 (In the text)
- Schechter, P. L., & Gunn, J. E. 1978, AJ, 83, 1360 [NASA ADS] [CrossRef] (In the text)
- Schinnerer, E., & Scoville, N. 2002, ApJ, 577, L103 [NASA ADS] [CrossRef] (In the text)
- Schirmer, M., Erben, T., Schneider, P., et al. 2003, A&A, 407, 869 [NASA ADS] [CrossRef] [EDP Sciences]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
- Schoenmakers, R. H. M., Franx, M., & de Zeeuw, P. T. 1997, MNRAS, 292, 349 [NASA ADS]
- Schwarz, U. J. 1985, A&A, 142, 273 (In the text)
- Schweizer, F., Whitmore, B. C., & Rubin, V. C. 1983, AJ, 88, 909 [CrossRef]
- Serra, P., Trager, S. C., van der Hulst, J. M., Oosterloo, T. A., & Morganti, R. 2006, A&A, 453, 493 [NASA ADS] [CrossRef] [EDP Sciences]
- Shane, W. W. 1977, BAAS, 9, 362 [NASA ADS]
- Shane, W. W. 1980, A&A, 82, 314 [NASA ADS]
- Shen, J., & Sellwood, J. A. 2006, MNRAS, 370, 2 [NASA ADS] (In the text)
- Simonson, G. F., & Tohline, J. E. 1983, ApJ, 268, 638 [NASA ADS] [CrossRef]
- Sparke, L. S. 1986, MNRAS, 219, 657 [NASA ADS] (In the text)
- Sparke, L. S., & Casertano, S. 1988, MNRAS, 234, 873 [NASA ADS] (In the text)
- Sparke, L. S., van Moorsel, G., Erwin, P., & Wehner, E. M. H. 2008, AJ, 135, 99 [NASA ADS] [CrossRef]
- Taniguchi, Y., Sofue, Y., Wakamatsu, K.-I., & Nakai, N. 1990, AJ, 100, 1086 [NASA ADS] [CrossRef]
- Tohline, J. E., & Durisen, R. H. 1982, ApJ, 257, 94 [NASA ADS] [CrossRef] (In the text)
- Tully, R. B., Pierce, M. J., Huang, J.-S., et al. 1998, AJ, 115, 2264 [NASA ADS] [CrossRef] (In the text)
- Ulrich, M.-H. 1975, PASP, 87, 965 [CrossRef] (In the text)
- van Albada, T. S., Kotanyi, C. G., & Schwarzschild, M. 1982, MNRAS, 198, 303 [NASA ADS] (In the text)
- van Driel, W., Arnaboldi, M., Combes, F., & Sparke, L. S. 2000, A&AS, 141, 385 [NASA ADS] [CrossRef] [EDP Sciences] (In the text)
- Varnas, S. R. 1990, MNRAS, 247, 674 [NASA ADS]
- Whitmore, B. C., Lucas, R. A., McElroy, D. B., et al. 1990, AJ, 100, 1489 [NASA ADS] [CrossRef]
Footnotes
- ... Administration
![[*]](/icons/foot_motif.gif)
- The NASA/IPAC Extragalactic Database (NED) is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
All Tables
Table 1: Basic properties of NGC 2685.
Table 2: Summary of observations and data reduction.
Table 3: Global best-fit tilted-ring parameters of NGC 2685.
Table 4: Basic properties of the detected dwarf galaxies in the vicinity of NGC 2685.
Table B.1: Velocities and masses of gas detected at ``anomalous'' velocities as derived from fitting a double-Gaussian to several profiles of the data cube.
Table C.1: Radially dependent best-fit parameters.
All Figures
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8.8cm]{9372_01a.eps}\i...
...72_01c.eps}\includegraphics[angle=270,width=8.8cm]{9372_01d.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg125.gif) |
Figure 1:
Top, left panel: logarithmic grey-scale plot of the i'-band image obtained with the INT. Top, right panel: grey-scale plot of the high-resolution H I total-intensity map. Bottom, left panel: low-resolution total-intensity H I map (contours and grey scale). Contours represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{9372_02a.eps}\includegraphi...
...idth=6cm]{9372_02d.eps}\includegraphics[width=6cm]{9372_02f.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg134.gif) |
Figure 2: Parametrizations of toy model data cubes and toy model total-intensity maps. Top panels: ``Flip model''. The orientation of the disk flips at a certain radius, the minimum requirement for speaking of a two-ring or two-disk system in NGC 2685. Bottom panels: ``Warp model''. Here a coherent but heavily warped disk is assumed. Left: surface brightness profile, rotation curve and disk orientation. SD: H I face-on column density/surface mass density. VROT: rotation velocity. INCL: inclination. PA: position angle. R: radius. Middle: three-dimensional visualizations of the disks. Right: toy model total-intensity maps. The lines trace the track along which the spectra in the position-velocity diagrams (PV-diagrams) shown in Fig. 3 are traced. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[angle=270]{9372_03a.eps}}...
...}\\
\resizebox{8cm}{!}{\includegraphics[angle=270]{9372_03c.eps}}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg135.gif) |
Figure 3: PV-diagrams along the lines across the minor axis of the inner ring shown in Fig. 2. Top panel: taken from the flip model data cube. Middle panel: taken from the original data cube. Bottom panel: taken from the warp-model data cube. The ellipses in the lower left corners denote the clean beam major axis ( HPBW) and the velocity resolution ( FWHM). The warp model is able to reproduce the connecting feature indicated by the ellipses, while the flip model is not. |
| Open with DEXTER | |
| In the text | |
 |
Figure 4:
Spectra taken from the low-resolution data cube at the positions indicated by the boxes in Fig. 1. Black: the original spectrum. Light grey (green in online version): fitted Gaussians. Dark grey (red in online version): residual after subtracting the fitted
Gaussians from the original profile. The velocity differences
|
| Open with DEXTER | |
| In the text | |
 |
Figure 5:
``Inclinogram'' of the NGC 2685 overlaid on the original total intensity maps: the ellipses mark the projection of the rings at radii of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=18cm]{9372_06.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg160.gif) |
Figure 6: Tilted-ring parametrization of the Spindle galaxy. SBR: surface brightness (upper limits only for the first two data points). VROT: rotation velocity. INCL: inclination (unconstrained at origin). PA: position angle (unconstrained at origin). R: radius. The vertical line denotes the optical radius r25. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=8.5cm]{9372_07a.eps} \...
...2_07c.eps} \includegraphics[angle=270,width=8.5cm]{9372_07d.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg163.gif) |
Figure 7:
Top panels: total-intensity contour plots ( left panel) and first-moment velocity fields ( right panel) derived from the low-resolution data cubes (dark-grey, blue in online version: original, light grey, pink in online version: model) overlaid on a
total-intensity grey-scale map derived from the observed data cube. The ellipse in the lower left corner represents the clean beam. The contours represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=6cm]{9372_08a.eps}\includegraphi...
...th=5.8cm]{9372_08b.eps}\includegraphics[width=6cm]{9372_08c.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg188.gif) |
Figure 8:
Tip-LON plots for the H I disk of NGC 2685. Left and right panel: tip-LON plots (see Briggs 1990 and Paper II), the filled circles are the projection of the tip of the normal vectors of the
rings at different radii onto a reference plane; the center of the
galaxy is denoted by a larger circle. The circles are drawn at
intervals of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm]{9372_09a.eps}\par {\h...
...includegraphics[angle=270,width=5.5cm]{9372_09b.eps}\hspace*{5mm}}\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg189.gif) |
Figure 9: Top panel: ``tiltogram'' of NGC 2685. This is a pixel map showing the mutual inclination of rings at different radii (see Paper II). Bottom panel: three-dimensional model of the H I disk of NGC 2685 according to the best-fit tilted-ring model. The model is rotated and artificially made opaque to again show the presence of an outer planar disk. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{9372_10.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg194.gif) |
Figure 10:
Difference- or residual velocity map derived by subtracting the model first-moment map from the original first-moment map. Overlaid are the projected rings of the best-fit model at radii
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=8.8cm,clip]{9372_11.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg243.gif) |
Figure 11:
H I total-intensity maps of the observed field overlaid on a DSS (red) image. From top to bottom: UGC 4683, two unknown possibly
merging objects, PGC 25002, NGC 2685. The contours represent the
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{9372_A1.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg258.gif) |
Figure A.1:
Selected images from the low-resolution data cube (channel width of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[angle=270,width=17cm]{9372_A2.eps}
\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg261.gif) |
Figure A.2:
Selected images from the high-resolution data cube (channel width of
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[angle=270,width=6.7cm]{9372_A3a.eps} \includegraphics[angle=270,width=6.7cm]{9372_A3b.eps} }\end{figure}](/articles/aa/full_html/2009/05/aa09372-08/Timg263.gif) |
Figure A.3:
Total-intensity map ( left) and first-moment velocity field ( right) derive from the high-resolution data cube overlaid on a total intensity grey-scale map. The ellipse in the lower left corner represents the clean beam. The contours represent the
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


