| Issue |
A&A
Volume 451, Number 1, May III 2006
|
|
|---|---|---|
| Page(s) | 237 - 249 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361:20054546 | |
| Published online | 25 April 2006 | |
The second-order asymptotic representation of higher-order non-radial p-modes in stars revisited
Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200 B, 3001 Leuven, Belgium
Received:
18
November
2005
Accepted:
23
January
2006
Aims. We improve the second-order asymptotic theory of higher-order non-radial p-modes in spherically symmetric stars that was developed by Smeyers et al. (1996) as an alternative for Tassoul's approach (1990).
Methods. Like the previous authors, we use asymptotic methods appropriate for singular perturbation problems, i.e. expansion procedures in terms of two variables and boundary-layer theory. However, in contrast with them, we no longer adopt boundary-layer coordinates near the singular boundary points that are identical to the fast variable used in the asymptotic expansions at larger distances.
Results. By our definitions of the boundary-layer coordinates, the matchings of the boundary-layer expansions to the asymptotic expansions valid at larger distances from the boundary points, and the constructions of the uniformly valid asymptotic expansions are more transparent.
Conclusions. The present
asymptotic theory confirms that the application of expansions in
terms of two variables and boundary-layer theory to the fourth-order
system of differential equations established by Pekeris (1938, ApJ, 88, 189) is
particularly appropriate for the construction of the asymptotic
representation of higher-order p-modes in spherically symmetric
stars. For these modes, the divergence of the Lagrangian
displacement is the basic function, and the radial component of the
Lagrangian displacement is of one order higher in the small
expansion parameter. In the lowest-order asymptotic approximation,
the divergence of the Lagrangian displacement obeys a second-order
differential equation of the Sturm-Liouville type. This property
explains that the eigenfunction that is associated with the nth
eigenfrequency displays  nodes, with
nodes, with 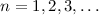
© ESO, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


