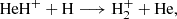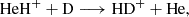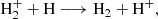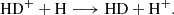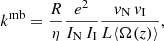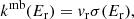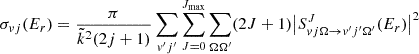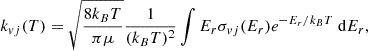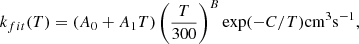| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202555316 | |
| Published online | 24 July 2025 | |
Letter to the Editor
Experimental confirmation of barrierless reactions between HeH+ and deuterium atoms suggests a lower abundance of the first molecules at very high redshifts
1
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
2
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, UMR-CNRS 5299, 34095 Montpellier Cedex, France
3
IPR – Université de Rennes Bât 11b, Campus de Beaulieu, 263 Avenue du Général Leclerc, 35042 Rennes Cedex, France
4
I. Physikalisches Institut, Justus-Liebig-Universität Gießen, D-35392 Gießen, Germany
5
Columbia Astrophysics Laboratory, Columbia University, New York, NY 10027, USA
6
Institute of Condensed Matter and Nanosciences, Université Catholique de Louvain, Louvain-la-Neuve B-1348, Belgium
⋆ Corresponding author: holger.kreckel@mpi-hd.mpg.de
Received:
28
April
2025
Accepted:
16
June
2025
The HeH+ ion was the first molecule to form in the early Universe, and its comparatively large dipole moment renders it a potential coolant, relevant during the epoch of first star formation. The main destruction mechanisms under primordial conditions are recombination with free electrons and chemical reactions with hydrogen atoms. The latter process was believed to be slow at low temperatures, owing to a barrier forming along the reaction coordinate. Here we present a joint experimental and theoretical study of the reaction HeH+ + D → HD+ + He that confirms the very recent proposition that the reaction is, in fact, barrierless and fast at low collision energies. The present evidence suggests that previous studies underestimated the low-temperature rate coefficient significantly because of an artifact in a widely used potential energy surface, and calls for a reassessment of the helium chemistry in the early Universe.
Key words: astrochemistry / molecular processes / early Universe / dark ages, reionization, first stars
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
The chemistry of the early Universe is dominated by the elements hydrogen, helium, and lithium, the only ones to form in substantial quantities during Big Bang nucleosynthesis. All of the light elements started out fully ionized, until the temperature dropped far enough for electrons to start recombining with nuclei to form neutral atoms. Owing to its high first ionization potential of 24.6 eV, helium was the first element to become neutral and engage in chemical reactions (Galli & Palla 2013). The first molecules were formed in the radiative association process H+ + He → HeH+ + hν (Lepp et al. 2002), and subsequently other small molecular ions and neutral molecules were formed, among them H , H2, H
, H2, H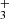 , LiH, LiH+, and deuterated variants of those species (Glover & Savin 2009).
, LiH, LiH+, and deuterated variants of those species (Glover & Savin 2009).
After the recombination era, the Universe cooled and expanded without fundamental changes in its phase or composition (the dark ages), until the first stars formed and re-ionized a large fraction of the baryonic matter. Simulations have shown that the existence of molecules is crucial at this stage. At temperatures below 10 000 K, the level spacing in all of the light atoms is too large to provide the necessary cooling (through photon emission) for a primordial protostar to collapse. Vibrational and rotational degrees of freedom in molecules, on the other hand, enable radiative cooling down to much lower temperatures (Saslaw & Zipoy 1967; Peebles & Dicke 1968; Bromm & Larson 2004).
As H2 lacks dipole-allowed transitions and HD features only a very small dipole moment of 0.00085 debye (Pachucki & Komasa 2008), infrared-active molecules with a much lower fractional abundance have been considered as potential coolants (Glover & Savin 2009). With a substantial dipole moment of 1.66 debye, the HeH+ ion becomes a valid cooling candidate.
While for very high redshifts (z > 300) the lifetimes of all molecular species are still severely limited by the radiation field, at redshifts of z < 300 the reactions responsible for the destruction of HeH+ change with the varying chemical conditions (Bovino et al. 2011b). For 20 < z < 300 collisions with atomic hydrogen are mainly responsible for the removal of HeH+ (Galli & Palla 2013), and at z < 20 the recombination with free electrons becomes the main destruction pathway (Bovino et al. 2011b).
Considering the intermediate range (20 < z < 300), simulations find that HeH+ engages in reactions with H or D atoms to form hydrogen molecular ions,
followed by charge exchange with atomic hydrogen,
This sequence contributes significantly to the formation of molecular hydrogen at early times (Galli & Palla 2013), before other pathways such as associative detachment of H− and H (Peebles & Dicke 1968; Kreckel et al. 2010) become efficient.
Reaction (1) is exothermic by 0.75 eV and has been the subject of theoretical calculations by several groups (Bovino et al. 2011b,a, 2012; Gamallo et al. 2014; Esposito et al. 2015; González-Lezana et al. 2019). All previous studies found that the reaction shows a rather uncharacteristic behavior for a barrierless ion-neutral process; namely, that it slows down considerably at low temperature. This is manifested in a decrease in the calculated rate coefficients by more than an order of magnitude between 1000 K and 10 K. However, recently some of us (Sahoo et al. 2024) have presented new calculations based on more accurate long-range interaction terms. These updated theoretical data strongly suggest that the reaction remains fast at low temperatures. Moreover, the new calculations indicate that the low-temperature decrease in the rate coefficient found in previous studies was caused by a fitting artifact of the multidimensional potential energy surface (PES), which led to an artificial barrier in the reaction coordinate.
Here, we present a combined experimental and theoretical investigation of Reaction (2). We chose the reaction between HeH+ and D atoms over the reaction with H atoms for technical reasons, as the detection of the HD+ reaction product has a much lower background in our experiment than the detection of H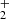 . However, since the PES is the same for both reactions, this does not limit the validity of our analysis. We corroborate this statement by comparing the cross section calculations employing the updated PES for reactions (1) and (2) in Sect. 4.
. However, since the PES is the same for both reactions, this does not limit the validity of our analysis. We corroborate this statement by comparing the cross section calculations employing the updated PES for reactions (1) and (2) in Sect. 4.
2. Merged-beams experiment
Our experiments employ the ion-neutral collision setup at the Cryogenic Storage Ring (CSR) of the Max Planck Institute for Nuclear Physics in Heidelberg. The properties of the storage ring as well as the ion-neutral collision experiment have been described in previous publications (von Hahn et al. 2016; Grussie et al. 2022, 2024a,b); here we give only a brief overview.
The CSR is an electrostatic storage ring with a circumference of 35.2 m, featuring a multilayer cryogenic design, whereby liquid helium is supplied to the innermost ultrahigh vacuum chambers. In cryogenic operation, the inner chambers have temperatures of around 6 K. Molecular ions with a permanent dipole moment will cool to their lowest rotational states within a few minutes of storage inside the CSR by spontaneous emission of radiation (O’Connor et al. 2016; Meyer et al. 2017; Kálosi et al. 2022).
The HeH+ ions are produced in a discharge (duoplasmatron) ion source, mass-selected by a dipole magnet, and accelerated to 85 keV by an electrostatic platform. We injected approximately 4 × 107 ions and stored them for up to 60 s. During this time, the HeH+ ions undergo radiative cooling and rapidly lose most of their internal excitation. Calculations show that already after 5 s of storage the ions occupy the two lowest rotational states with j ≤ 1 (see Appendix A).
During storage the ions are phase-space cooled by the CSR electron cooler. To this end a nearly monoenergetic velocity-matched electron beam with a kinetic energy of 9.3 eV (in the laboratory frame) is superimposed collinearly to the ion beam. Through Coulomb interactions with the electrons, the ion beam is cooled translationally (Poth 1990), which leads to a lower beam emittance, manifested in a smaller diameter and smaller angular divergence. Apart from translational beam cooling, we do not expect a significant impact of the electron beam on the internal state of the stored ions, since the electron recombination rate coefficient and inelastic electron collisions are slow, compared to the fast radiative cooling of HeH+ (Novotný et al. 2019).
The neutral atomic D beam is produced by photodetachment of a D− anion beam. Photodetachment using infrared diode laser stacks will result in the production of ground state D atoms only (O’Connor et al. 2015). The D− ions are produced in a duoplasmatron ion source and accelerated electrostatically to 30 keV before being directed toward the photodetachment zone. Here, the field of a strong (2 kW) continuous diode laser array at 808 nm neutralizes approximately 4% of the ion beam. The remaining D− ions are deflected into a Faraday cup, while the neutralized ground-state D atoms enter the CSR.
The photodetachment takes place inside a voltage-variable drift tube, and the photodetachment zone is bounded by two round 4.5 mm apertures, which are 2.9 m apart. By applying a static voltage to the drift tube, the anions can be accelerated or decelerated just prior to the neutralization process, allowing one to adjust the relative collision energy between the HeH+ and the D beams (see Grussie et al. (2022)). At a drift tube setting of +4 kV, the 30 keV D− beam is accelerated to 34 keV and the HeH+ ions and the neutral D beams are velocity-matched with a laboratory frame kinetic energy of 17 keV/u. By detuning the drift tube voltage, we sampled collision energies, Er, in the center-of-mass frame between 0 and 20 eV. Our simulations (Grussie et al. 2022) indicate that the lowest collision energy achievable in the present measurement using an electron-cooled ion beam is 30 meV.
The D atoms traverse the straight injection section of the storage ring, where they overlap with the stored HeH+ ions for ∼4.5 m. The neutral beam flux is recorded using secondary-electron emission inside an external Faraday cup. The photodetachment laser (and thus the neutral beam) is switched on and off with a period of 30 ms for background subtraction.
The charged HD+ products of Reaction (2) with a kinetic energy of ∼51 keV (for velocity-matched beams) are separated from the HeH+ ions by the first 6-degree deflector after the interaction zone (von Hahn et al. 2016; Grussie et al. 2022) and their count rate, R, is recorded by a movable single-particle detector.
The result of the measurements is a merged-beams rate coefficient, kmb, given by
where η denotes the product detection efficiency; e stands for the unit charge; vN and vI represent the velocities of the neutral atoms and the ions, respectively; and L⟨Ω(z)⟩ denotes the product of the length of the interaction section, L, and the averaged overlap form factor, ⟨Ω(z)⟩ (Grussie et al. 2022). The neutral flux (as in previous merged-beams studies, we interpret the neutral flux as a current, see, e.g., Bruhns et al. 2010a,b; Miller et al. 2012) and the current attributed to the circulating ions are given by IN and II, respectively. In the present experiment, we performed only relative rate coefficient measurements, and thus only those parameters that change during the measurements were monitored and recorded; namely, R, vN, vI, IN, and II. The detection efficiency and the beam overlap remained constant during the experiment.
3. Theoretical calculations
The theoretical calculations for Reaction (2) were performed by means of both time-independent quantum mechanical (TIQM) and quasi-classical trajectory (QCT) methods. The calculations were based on a refined global PES of the electronic ground state of HeH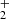 , which incorporates accurate long-range interaction terms, removing the artificial barrier present in the widely used PES of Ramachandran et al. (2009). A detailed description of the refined PES has been presented in Sahoo et al. (2024).
, which incorporates accurate long-range interaction terms, removing the artificial barrier present in the widely used PES of Ramachandran et al. (2009). A detailed description of the refined PES has been presented in Sahoo et al. (2024).
The TIQM calculations were performed using the ABC code of Manolopoulos and colleagues (Skouteris et al. 2000). The time-independent nuclear Schrödinger equation was solved for the triatomic reactive system using a coupled-channel approach in hyperspherical coordinates. The diatomic rovibrational wave functions including the helicity states (both open and closed) of all available reactive channels were used to construct the coupled-channel basis functions. The set of coupled-channel hyperradial equations was solved by the constant reference potential log-derivative method (Manolopoulos 1986) and the scattering matrix (S matrix) was obtained by applying asymptotic boundary conditions at large hyperradii. The S matrix was calculated in a specific energy range for a particular value of the total angular quantum number, J, diatomic parity, p, and triatomic parity, P. Converged numerical parameters used in the ABC code to generate cross sections, σ, in various energy ranges are given in Appendix B.
The QCT methodology is reviewed in detail in Truhlar & Muckerman (1979) and the QCT calculations are performed by solving the classical Hamilton’s equations for the nuclear motion on the PES with the QCT code of some of the authors (Bossion et al. 2018). For this study, instead of the standard histogram binning, we used a modified Gaussian binning that was described in a previous QCT study of the same system using the PES of Ramachandran et al. (González-Lezana et al. 2019). We ensured the convergence of the maximum impact parameter for each energy by running small batches of trajectories beforehand. The numerical parameters used in the QCT code are given in Appendix C.
The state-specific energy-dependent rate coefficients for comparison with the merged-beams results are obtained as
where vr is the nominal relative velocity of the collision. While the experiment actually samples a velocity distribution (Grussie et al. 2022), Eq. (6) is a very good approximation for cross sections without sharp features that exhibit smooth behavior with velocity, as was found for the present reaction.
4. Results
Figure 1 shows our measured merged-beams rate coefficient, kmb. During the experimental campaign we expected the rate coefficient to drop at low collision energies, as was predicted by all previous theoretical studies. However, to our surprise we observed a fast reaction rate coefficient that appeared completely independent of the collision energy below 3 eV. We used a new movable detector based on a converter plate and a stack of micro channel plates. The detector is located inside the CSR cryogenic vacuum, and the detection efficiency has not been calibrated on an absolute level. Therefore, we normalized the absolute scale of the experimental data to the energy-independent Langevin rate coefficient (Gioumousis & Stevenson 1958) for Reaction (2) at collision energies < 1 eV.
 |
Fig. 1. Merged-beams rate coefficient for the reaction HeH+ + D → HD+ + He as a function of the relative collision energy, Er. The experimental values for storage times from 5 to 60 s (black markers) have been normalized to the Langevin rate coefficient (dashed line). The error bars display statistical uncertainties on a 90% confidence level. Our new theoretical TIQM calculations for HeH+ ions in j = 0 and j = 1 are shown by the light blue and green lines, respectively. Our QCT calculations are shown by the solid dark blue (j = 0) and green (j = 1) lines with markers. The uncertainties for the QCT values were derived from the statistics of the trajectory calculations. |
We find the low-energy behavior to be fully compatible with the concept of a barrierless ion-neutral reaction, while the drop in the rate coefficient at higher energies is caused by the opening of dissociative reaction channels, leading to a three-body break-up into H + D+ + He or H+ + D + He. These channels become energetically open at energies of Er > 1.9 eV, and therefore they are not as relevant for astrophysical environments. Since we detect the HD+ product of Reaction (2) directly, contributions from dissociative channels are not recorded in our measurements.
Also shown are our new TIQM and QCT theoretical calculations for HeH+ + D collisions, based on the refined PES described in Sahoo et al. (2024). The experimental finding of a near-constant rate coefficient at low energies is in very good agreement with both the TIQM and QCT calculations. We show rate coefficients for HeH+ ions in rotational states j = 0 and j = 1, which are the only states with a significant population after 5 s of storage of the ions inside the CSR (Fig. A.1). The predicted difference in the rate coefficient between the two lowest rotational states is small. The QCT calculations extend to higher collision energies, and they reproduce the drop in the rate coefficient observed in the experiment.
Figure 2 compares both our experimental and theoretical reaction cross sections with previous calculations for HeH+ + H collisions. To this end we divided the measured merged-beams rate coefficient by the nominal relative velocity, vr, between the neutral and ion beams (see Eq. (6)). In doing so we neglected the energy spread of both beams, which – apart from the very lowest collision energies – constitutes a very good approximation, in particular for the essentially energy-independent rate coefficient at low collision energies found for the present reaction.
 |
Fig. 2. Reaction cross section, σ, for the HeH+ + D → HD+ + He reaction as a function of the collision energy, Er. The experimental results (black markers) are compared to our theoretical TIQM and QCT results. Also shown are TIQM and QCT calculations for HeH+ + H → H |
While our new calculations and the experimental data fully agree within the error margins, the previous calculations of Bovino et al. (2011b), Esposito et al. (2015), and González-Lezana et al. (2019) deviate substantially at low energies. As is explained in detail in Sahoo et al. (2024), this discrepancy in the behavior of the cross section at low collision energies can be traced to an artificial barrier caused by a fitting artifact in the PES of Ramachandran et al. (2009) used in those studies. The effect of the barrier already becomes noticeable at energies significantly higher than the nominal height of the barrier, as for larger impact parameters the centrifugal potential induced by the angular momentum adds to the effective barrier height and blocks higher partial waves (see Song & Guo 2023 for insights into reactions with submerged barriers).
To enable the use of the experimentally confirmed rate coefficients in models of primordial chemistry, we have converted the theoretical cross sections into gas kinetic temperature rate coefficients. Figure 3 shows the kinetic temperature rate coefficients derived for the reaction of HeH+ with both atomic isotopes (Reactions (1) and (2)), compared to the respective Langevin rates and to previous calculations, which were still affected by the artificial barrier. The new calculations show only slight deviations from the classical Langevin rate below 10 000 K, while the rates derived from previous calculations deviate by a factor of two at 100 K and by more than an order of magnitude at 10 K.
 |
Fig. 3. Kinetic temperature rate coefficients for the reactions HeH+ + D → HD+ + He and HeH+ + H → H |
There are two previous measurements of Reaction (1) in the literature. Crossed-beam measurements are reported by Rutherford & Vroom (1973), albeit at high collision energies (1–25 eV) and with an undefined internal excitation of the HeH+ ions. The resulting cross sections were found to be a factor of 2.4 smaller than previous calculations (even though these calculations were still affected by the artificial barrier), and had to be scaled up for a qualitative comparison to the theory (De Fazio 2014). The room temperature data of Karpas et al. (1979) resulted in a rate coefficient of (9.1 ± 2.5) ×10−10 cm3 s−1. The measurement was carried out with internally hot HeH+ ions and the rate coefficient was normalized to another measurement, which, in turn, was also performed with molecular ions of undefined internal excitation. We believe that a comparison of these data to our calculations with internally cold ions is of very limited merit, as recent experiments have shown that absolute rate coefficients depend critically on internal excitation (Grussie et al. 2024a).
We have fit the kinetic temperature rate coefficients for both reactions with our own modification of the Arrhenius–Kooij formula (Wakelam et al. 2012) to facilitate the implementation in astrophysical models and databases. The fit parameters are listed in Appendix D.
5. Summary and conclusions
We have carried out merged-beams measurements of the reaction between ground term D atoms and rotationally cold HeH+ ions stored inside the CSR. Our energy-resolved measurements support the recent theoretical finding of Sahoo et al. (2024) that reactions between atomic hydrogen and HeH+ ions remain efficient at low temperature, in contrast to previous theoretical calculations. The reason for this discrepancy has been identified by Sahoo et al. (2024) as an artificial barrier in the parametrization of the PES of Ramachandran et al. (2009). As the PES is the same for Reactions (1) and (2), the significance of our experimental results extends to both reactions.
We used the experimentally confirmed theoretical cross sections to provide kinetic temperature rate coefficients for Reactions (1) and (2). These reactions are the dominant destruction mechanisms for HeH+ at redshifts of 20 < z < 300, where both processes also constitute an important pathway for the formation of molecular hydrogen (H2 and HD) under primordial conditions (Galli & Palla 2013). At later times (z < 20), when the formation of the first stars sets in, the recombination with free electrons is expected to dominate the removal of HeH+ (Bovino et al. 2011b). However, measurements at the CSR have recently shown that the electron recombination rate is very slow for rotationally cold HeH+ ions (Novotný et al. 2019). Combined with the present finding, it is apparent that reactions of HeH+ with atomic hydrogen are more important for primordial molecular abundances than was previously assumed and that reevaluations of helium chemistry in the early Universe – as well as very recent modeling efforts (Sil et al. 2025) of HeH+ detections in planetary nebulae (Güsten et al. 2019; Neufeld et al. 2020) – may be called for.
Acknowledgments
This work was supported by the Max Planck Society. X.U. is a Senior Research Associate of the Fonds de la Recherche Scientifique – FNRS, and acknowledges support under grant no. 4.4504.10. This work has been supported by the Agence Nationale de la Recherche (ANR-HYTRAJ) under Contract No. ANR-19-CE30-0039-01. Y.S., D.B and J.S. acknowledge support from the High Performance Computing Platform MESO@LR at University of Montpellier.
References
- Bossion, D., Scribano, Y., Lique, F., & Parlant, G. 2018, MNRAS, 480, 3718 [Google Scholar]
- Bovino, S., Tacconi, M., & Gianturco, F. A. 2011a, J. Phys. Chem. A, 115, 8197 [Google Scholar]
- Bovino, S., Tacconi, M., Gianturco, F. A., & Galli, D. 2011b, A&A, 529, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovino, S., Gianturco, F. A., & Tacconi, M. 2012, Chem. Phys. Lett., 554, 47 [Google Scholar]
- Bromm, V., & Larson, R. B. 2004, ARA&A, 42, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Bruhns, H., Kreckel, H., Miller, K., et al. 2010a, Rev. Sci. Instrum., 81, 0131121 [Google Scholar]
- Bruhns, H., Kreckel, H., Miller, K. A., Urbain, X., & Savin, D. W. 2010b, Phys. Rev. A, 82, 042708 [Google Scholar]
- Coppola, C. M., Lodi, L., & Tennyson, J. 2011, MNRAS, 415, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Datz, S., & Larsson, M. 1992, Phys. Scr., 46, 343 [Google Scholar]
- De Fazio, D. 2014, Phys. Chem. Chem. Phys., 16, 11662 [Google Scholar]
- Esposito, F., Coppola, C. M., & De Fazio, D. 2015, J. Phys. Chem. A, 119, 12615 [Google Scholar]
- Galli, D., & Palla, F. 2013, ARA&A, 51, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Gamallo, P., Akpinar, S., Defazio, P., & Petrongolo, C. 2014, J. Phys. Chem. A, 118, 6451 [Google Scholar]
- Gioumousis, G., & Stevenson, D. P. 1958, J. Chem. Phys., 29, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Savin, D. W. 2009, MNRAS, 393, 911 [NASA ADS] [CrossRef] [Google Scholar]
- González-Lezana, T., Bossion, D., Scribano, Y., Bhowmick, S., & Suleimanov, Y. V. 2019, J. Phys. Chem. A, 123, 10480 [Google Scholar]
- Grussie, F., Berger, L., Grieser, M., et al. 2024a, Phys. Rev. A, 109, 062804 [Google Scholar]
- Grussie, F., Berger, L., Grieser, M., et al. 2024b, Phys. Rev. Lett., 132, 243001 [Google Scholar]
- Grussie, F., O’Connor, A. P., Grieser, M., et al. 2022, Rev. Sci. Instrum., 93, 053305 [Google Scholar]
- Güsten, R., Wiesemeyer, H., Neufeld, D., et al. 2019, Nature, 568, 357 [CrossRef] [Google Scholar]
- Kálosi, A., Grieser, M., von Hahn, R., et al. 2022, Phys. Rev. Lett., 128, 183402 [Google Scholar]
- Karpas, Z., Anicich, V., & Huntress, W. T. 1979, J. Chem. Phys., 70, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, H., Bruhns, H., Čížek, M., et al. 2010, Science, 329, 69 [Google Scholar]
- Lepp, S., Stancil, P. C., & Dalgarno, A. 2002, J. Phys. B At. Mol. Opt. Phys., 35, R57 [Google Scholar]
- Manolopoulos, D. E. 1986, J. Chem. Phys., 85, 6425 [Google Scholar]
- Meyer, C., Becker, A., Blaum, K., et al. 2017, Phys. Rev. Lett., 119, 023202 [Google Scholar]
- Miller, K. A., Bruhns, H., Čížek, M., et al. 2012, Phys. Rev. A, 86, 032714 [Google Scholar]
- Neufeld, D. A., Goto, M., Geballe, T. R., et al. 2020, ApJ, 894, 37 [CrossRef] [Google Scholar]
- Novotný, O., Wilhelm, P., Paul, D., et al. 2019, Science, 365, 676 [CrossRef] [Google Scholar]
- O’Connor, A. P., Grussie, F., Bruhns, H., et al. 2015, Rev. Sci. Instrum., 86, 113306 [Google Scholar]
- O’Connor, A. P., Becker, A., Blaum, K., et al. 2016, Phys. Rev. Lett., 116, 113002 [Google Scholar]
- Pachucki, K., & Komasa, J. 2008, Phys. Rev. A, 78, 052503 [Google Scholar]
- Peebles, P. J. E., & Dicke, R. H. 1968, ApJ, 154, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Poth, H. 1990, Phys. Rep., 196, 135 [Google Scholar]
- Ramachandran, C. N., Fazio, D. D., Cavalli, S., Tarantelli, F., & Aquilanti, V. 2009, Chem. Phys. Lett., 469, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Rutherford, J. A., & Vroom, D. A. 1973, J. Chem. Phys., 58, 4076 [Google Scholar]
- Sahoo, J., Bossion, D., González-Lezana, T., Talbi, D., & Scribano, Y. 2024, J. Chem. Phys., 161, 144312 [Google Scholar]
- Saslaw, W. C., & Zipoy, D. 1967, Nature, 216, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Sil, M., Faure, A., Wiesemeyer, H., et al. 2025, A&A, 695, A244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skouteris, D., Castillo, J., & Manolopoulos, D. 2000, Comput. Phys. Commun., 133, 128 [Google Scholar]
- Song, H., & Guo, H. 2023, ACS Phys. Chem. Au, 3, 406 [Google Scholar]
- Strasser, D., Bhushan, K. G., Pedersen, H. B., et al. 2000, Phys. Rev. A, 61, 060705 [Google Scholar]
- Truhlar, D. G., & Muckerman, J. T. 1979, in Reactive Scattering Cross Sections III: Quasiclassical and Semiclassical Methods, ed. R. B. Bernstein (Boston: Springer, US), 505 [Google Scholar]
- von Hahn, R., Becker, A., Berg, F., et al. 2016, Rev. Sci. Instrum., 87, 063115 [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [Google Scholar]
Appendix A: Internal cooling of HeH+
Molecular ions produced in discharge ion sources typically feature very high internal excitations, corresponding to internal temperatures of up to several thousand kelvin (although the excitation does not necessarily have to be thermal). However, owing to their comparatively large dipole moment, HeH+ ions cool rapidly inside the CSR by spontaneous emission of radiation. All vibrationally excited states will decay within the first 200 milliseconds of storage (Datz & Larsson 1992). The lifetime of HeH+ in the metastable electronic triplet state was also found to be in the range of hundreds of milliseconds in previous experiments (Strasser et al. 2000), and no trace of this state was found in the imaging data of previous CSR measurements (Novotný et al. 2019), where it would have stood out clearly in the kinetic energy release spectrum. The time evolution of the rotational states, on the other hand, is considerably slower, but straightforward to predict (Novotný et al. 2019), using known transition strengths and level energies (Coppola et al. 2011). Figure A.1 shows the simulated evolution of the rotational states during storage inside the CSR. Already after 5 s of storage, we expect all population to have accumulated in the two energetically lowest quantum states of the molecule (j ≤ 1).
 |
Fig. A.1. Calculated evolution of the population of rotational states of HeH+ ions during storage inside the CSR. The simulation is based on the published transition strengths and level energies of Coppola et al. (2011). The calculation is the same as presented by Novotný et al. (2019), where the initial distribution represents a thermal ensemble at 3000 K. However, the exact choice of the initial temperature is largely irrelevant, as all highly excited states decay very quickly compared to the storage times of up to 60 s that were sampled in the present experiment. |
Appendix B: Details on TIQM calculations
In Table B.1 specific parameters used for the generation of reaction cross sections with the ABC code are listed. Extensive convergence tests are carried out for all parameters in each Er range as given in Table B.1. The convergence of the cross section is checked with respect to the maximum number of rotational states in any reactive channel (jmax), the maximum total energy that includes all open and closed rovibrational levels in the basis set (Emax), the maximum value of the hyperradius (ρmax), the number of log derivative propagation sectors (nsec), the helicity truncation parameter (kmax) and the maximum total angular momentum (Jmax).
Parameters for HeH+ (v = 0, j = 0, 1) used in the ABC code.
The state-specific cross section is calculated from the S-matrix elements as
Here, 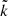 =
=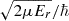 , with μ being the atom-diatom reduced mass of the reactant arrangement, Er is the relative collision energy. The symbols v, j, and Ω denote the vibrational, rotational, and helicity quantum numbers of the reactant channel, respectively, and the corresponding prime quantities denote the same for the product channel. The relative velocity can be obtained from
, with μ being the atom-diatom reduced mass of the reactant arrangement, Er is the relative collision energy. The symbols v, j, and Ω denote the vibrational, rotational, and helicity quantum numbers of the reactant channel, respectively, and the corresponding prime quantities denote the same for the product channel. The relative velocity can be obtained from 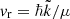 .
.
Appendix C: Details on QCT calculations
In Table C.1, the maximum impact parameters used for the QCT calculations are listed. For each energy range considered, the maximum impact parameter is determined using 200 trajectories. Fine convergence is then achieved considering for each trajectory the following condition on the continuous rotational quasi-quantum number 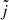 of HeH+ and the initial quantum number j:
of HeH+ and the initial quantum number j: 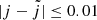 . Collisional energies from 1 meV to 21.5 eV were considered, with 10 000 trajectories propagated for each of the 27 energy steps (6 energy steps per order of magnitude, with a logarithmic increment).
. Collisional energies from 1 meV to 21.5 eV were considered, with 10 000 trajectories propagated for each of the 27 energy steps (6 energy steps per order of magnitude, with a logarithmic increment).
Impact parameter for various energy windows.
Appendix D: Kinetic temperature rate coefficients
The kinetic temperature rate coefficients are calculated from reaction cross sections by thermal averaging over a Maxwell-Boltzmann velocity distribution according to
where kB is the Boltzmann constant. Converged rate coefficients are obtained for temperatures from 10 to 40 000 K by combining both TIQM and QCT cross sections from low and high energy regions, respectively. The merging is done around the Er range of 1−2 eV, where both TIQM and QCT cross sections are virtually indistinguishable. This ensures the validity of the resulting (TIQM+QCT) rate coefficients over a broad range of temperature.
To provide data for astrochemical databases the j = 0 and j = 1 rate coefficients for both the isotopic Reactions (1) and (2) are fit to our own modification of the Arrhenius-Kooij formula (Wakelam et al. 2012),
the A0, A1, B and C fit parameters are listed in Table C.2. We used the Levenberg-Marquardt algorithm as implemented in SciPy’s scipy.optimize.curve_fit function to optimize the parameters. The deviation between the calculated rate coefficients and the fits using the modified Arrhenius-Kooij formula is less than 2% at all energies, which should be sufficient for astrophysical models.
Fit parameters for the kinetic temperature rate coefficients kvj(T) using Eq. D.2.
All Tables
Fit parameters for the kinetic temperature rate coefficients kvj(T) using Eq. D.2.
All Figures
 |
Fig. 1. Merged-beams rate coefficient for the reaction HeH+ + D → HD+ + He as a function of the relative collision energy, Er. The experimental values for storage times from 5 to 60 s (black markers) have been normalized to the Langevin rate coefficient (dashed line). The error bars display statistical uncertainties on a 90% confidence level. Our new theoretical TIQM calculations for HeH+ ions in j = 0 and j = 1 are shown by the light blue and green lines, respectively. Our QCT calculations are shown by the solid dark blue (j = 0) and green (j = 1) lines with markers. The uncertainties for the QCT values were derived from the statistics of the trajectory calculations. |
| In the text | |
 |
Fig. 2. Reaction cross section, σ, for the HeH+ + D → HD+ + He reaction as a function of the collision energy, Er. The experimental results (black markers) are compared to our theoretical TIQM and QCT results. Also shown are TIQM and QCT calculations for HeH+ + H → H |
| In the text | |
 |
Fig. 3. Kinetic temperature rate coefficients for the reactions HeH+ + D → HD+ + He and HeH+ + H → H |
| In the text | |
 |
Fig. A.1. Calculated evolution of the population of rotational states of HeH+ ions during storage inside the CSR. The simulation is based on the published transition strengths and level energies of Coppola et al. (2011). The calculation is the same as presented by Novotný et al. (2019), where the initial distribution represents a thermal ensemble at 3000 K. However, the exact choice of the initial temperature is largely irrelevant, as all highly excited states decay very quickly compared to the storage times of up to 60 s that were sampled in the present experiment. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.