| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202453274 | |
| Published online | 06 February 2025 | |
Letter to the Editor
Populations of neutron star ultraluminous X-ray sources
Mind your bs and Bs
1
Institut d’Estudis Espacials de Catalunya (IEEC), Edifici RDIT, Campus UPC, 08860 Castelldefels (Barcelona), Spain
2
Institute of Space Sciences (ICE, CSIC), Campus UAB, Carrer de Magrans, 08193 Barcelona, Spain
3
Department of Physics, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
4
INAF – Osservatorio Astronomico di Roma, via Frascati 33, I-00078 Monte Porzio Catone, Italy
⋆ Corresponding author; kovlakas@ice.csic.es
Received:
3
December
2024
Accepted:
15
January
2025
Ultraluminous X-ray sources (ULXs) with neutron star (NS) accretors pose a challenge to traditional accretion models, sparking a debate regarding the role of geometrical beaming and strong magnetic fields (B). The reduction of the Thomson cross-section in the presence of strong B leads to a modification of the Eddington limit; therefore, it is expected to affect significantly the observational appearance of NS-ULXs. We investigate the role of this modification using population synthesis models and explore its effects on the X-ray luminosity functions, spin-up rates, and outflow energetics of the observed NS-ULXs. Our results show that the new prescription allows NS-ULXs to achieve super-Eddington luminosities with a milder beaming compared to before, improving the agreement with observations. In addition, it broadens the range of spin-up rates, allowing for more diverse conditions in NS-ULXs in terms of accretion rates and magnetic fields. More importantly, the reduced beaming increases the likelihood of observing the NS-ULXs within wind-powered nebulae, such as NGC 5907 ULX-1. Our findings highlight the need to take B effects into account, independently of the usual approach based on geometrical beaming or strong B. Finally, we call for magnetospheric accretion prescriptions that can be integrated in population synthesis codes.
Key words: accretion, accretion disks / magnetic fields / stars: black holes / stars: evolution / stars: neutron / X-rays: binaries
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Ultraluminous X-ray sources (ULXs) are accreting compact objects, distinct from active galactic nuclei, with luminosities ranging from 1039 to 1042 erg s−1 (e.g., Kaaret et al. 2017; King et al. 2023). Based on the Eddington limit and assuming pure hydrogen material, we have
where M1 is the mass of the accretor in solar units (M⊙), ULXs could represent accreting black holes (BHs) with M1 ∼ 10 − 104. However, their association with star-forming regions suggests they are X-ray binaries (e.g., Zezas et al. 2002), where accretors tend to have lower masses (≲20 M⊙; Miller-Jones et al. 2021). Consequently, the majority of ULXs are now thought to be super-Eddington accretors.
The Shakura & Sunyaev (1973) model for super-critical accretion onto BHs, where the mass-transfer rate Ṁtr exceeds the Eddington rate ṀEdd, describes an accretion disk that is locally Eddington-limited at all radii and becomes geometrically thick near the accretor. This model predicts strong outflows, and a bolometric luminosity higher than the LEdd value,
where ṁ = Ṁtr/ṀEdd is the Eddington ratio and LEdd = 0.1ṀEddc2, adopting accretion efficiency 0.1 (Frank et al. 2002; for completeness, the sub-Eddington regime, ṁ < 1, is also included). We note that Eq. (2) does not take into account the role of advection (e.g., Beloborodov 1998; Chashkina et al. 2019), which may decrease the bolometric luminosity by a factor of ∼30 − 40% (e.g., Lipunova 1999; Poutanen et al. 2007). Still, luminosities of ≳1040 erg s−1 cannot be accounted for by the lnṁ term. Instead, they are better explained by the collimation of the radiation escaping through a funnel formed by the outflows (King et al. 2001). As a result, the observed luminosity under the isotropic emission, Liso, is
where the beaming factor, b, represents the fraction of the full solid angle through which radiation escapes. Here, b is known to be correlated with ṁ (King 2009),
allowing for extreme luminosities without invoking extreme BH masses (e.g., 1042 erg s−1 for M1 = 30 and ṁ = 60).
The discovery of pulsating ULXs (PULXs; Bachetti et al. 2014) confirmed the existence of neutron star (NS) ULXs, often exhibiting highly super-Eddington luminosities. The most extreme example, NGC 5907 ULX-1, reached Liso/LEdd ∼ 1000 (Israel et al. 2017) and, under the beaming scenario, this corresponds to small b < 10−2. Such low b values are inconsistent with the sinusoidal profiles in PULXs (e.g., Kaaret et al. 2017) and have not been reproduced via numerical simulations (e.g., Abarca et al. 2021). This has prompted investigations into alternative scenarios, primarily focusing on the role of the “usual suspect” in NSs, namely: the magnetic field (e.g., Eksi et al. 2015).
In the presence of strong magnetic fields, the Thomson cross-section is reduced for photon energies below the cyclotron energy (Herold 1979), increasing the Eddington limit to a critical luminosity (e.g., Paczynski 1992; Dall’Osso et al. 2015; Brightman et al. 2018) of
where B12 is the dipolar magnetic field in units of 1012 G. Consequently, NS-ULXs could be sub-Eddington accretors with B12 ∼ 10 − 1000 without beamed emission. However, this interpretation relies on highly magnetised NSs, which could push many PULXs in the propeller regime, where infalling matter is expelled rather than accreted.
Whether the observational appearance of PULXs can be explained by beaming or extreme Bs is a matter of debate since their discovery. Arguments in favour of the beaming are: (i) the high-B scenario requires B12 ≳ 100 (e.g., Lasota & King 2023), higher than the typical values in X-ray binaries and constraints in PULXs (e.g., Walton et al. 2018; Middleton et al. 2019; ii) collimated emission in NS-ULX simulations (e.g., Mushtukov et al. 2019; Inoue et al. 2023) and its consequences for the spectra of ULXs (e.g., Poutanen et al. 2007; King 2009; iii) the extension of the X-ray luminosity function (XLF) to the ULX regime, reproduced by population synthesis studies employing beaming, in star-forming galaxies (e.g., Misra et al. 2023), including BH-dominated low-metallicity galaxies (e.g., Wiktorowicz et al. 2019), and in NS-dominated passive galaxies agreeing with ULX demographic studies (e.g., Kovlakas et al. 2020).
Conversely, the high-B scenario (B12 ≳ 100) has been supported by the following points: (i) expanding nebulæ near ULXs have been found to require mechanical power, in terms of outflow kinetic power (Lkin), similar to the observed luminosity of the ULXs (e.g., Holmberg II X-1; Pakull & Mirioni 2002). This suggests that the inferred luminosities are not overestimated due to strong beaming (e.g., Lkin ∼ 1.3 × 1041 erg s−1 in NGC 5907 ULX-1; Belfiore et al. 2020; ii) the orbital decay observed in M82 X-2 points at Ṁtr ≫ ṀEdd, while the mass available to the accretor is sufficient to explain its luminosity (e.g.; Bachetti et al. 2022, however, also see King & Lasota 2021), as well as mild beaming hinted by the long-term spin-down rate of the system (Liu 2024; iii) extreme beaming implies a large population of hidden ULXs, challenging to reproduce in population synthesis models which often force a b limit (e.g., > 0.0032; Wiktorowicz et al. 2019; Misra et al. 2023); and (iv) strong beaming precludes the detection of pulsations due to the reflections of X-ray photons in a geometrically thick inner accretion wall (e.g., Mushtukov et al. 2021; Mushtukov & Portegies Zwart 2023).
It has been suggested that the observational appearance of PULXs may be explained by the combined effect of B on LEdd, the presence of multipolar components, and moderate beaming (e.g., Israel et al. 2017; Erkut et al. 2020). To date, however, there has been no comprehensive prescription devised for the magnetic field configuration of NSs and magnetospheric accretion that would be applicable to both sub-Eddington and super-Eddington regimes. Consequently, the models of Shakura & Sunyaev (1973), Poutanen et al. (2007), King (2009) are commonly employed in observational (e.g., Middleton et al. 2019) and theoretical studies (e.g., Lasota & King 2023), as well as in population synthesis models (e.g., Wiktorowicz et al. 2019; Misra et al. 2023, 2024).
In this Letter, we evaluate whether the combination of the modified LEdd, B and beaming reconciles the observations discussed above, using population synthesis models. Finally, we highlight the importance of integrating in the models up-to-date magnetospheric accretion prescriptions towards a self-consistent framework for the study of NS-ULXs.
2. Methodology
In the following paragraphs, we describe the calculation of the observable quantities (Liso, 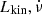 ) in simulated systems, as well as the setup of our population synthesis models.
) in simulated systems, as well as the setup of our population synthesis models.
2.1. Observables
The B-dependent critical luminosity acts as a new Eddington limit, only if Lcrit > LEdd (Paczynski 1992):
by combining Eqs. (1) and (5). Then, Eqs. (1)–(4) are applied to estimate the apparent luminosity, Liso, for both BHs and NSs, but now the ṁ value is determined relative to the LEdd, B for NSs.
The mechanical feedback (Lkin) is challenging to model due to its dependence on the outflow rate and speed, both of which vary as functions of the launching radius. This distribution is shaped by the accretion geometry and Ṁtr. To estimate Lkin at an order-of-magnitude level, we assume that matter is accreted at approximately the Eddington rate (however it can exceed it by a factor of 6 in NSs; Basko & Sunyaev 1976; Kaaret et al. 2017), while the rest of the transferred mass is expelled with speed ≈0.2 c (e.g., Pinto et al. 2016):
The spin-up rate 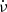 in NSs is the result of the torque from the accreted material at rate Ṁ (at RM):
in NSs is the result of the torque from the accreted material at rate Ṁ (at RM):
where I ≈ 1045 g cm2 is the moment of inertia. Here, RM is the magnetospheric radius,
where μ = BR3 is the magnetic moment with dipolar field, B, and radius, R. On this basis, we get
where the accretion rate, Ṁ17 (at RM), magnetic field, B, radius, R6, and mass, M1, are in units of 1017 g s−1, 1012 G, 106 cm, and 1 M⊙, respectively. We notice that Eq. (10) is consistent with Shapiro & Teukolsky (1983), but with a larger scaling than the expressions in King et al. (2017) and Lasota & King (2023), as well as a typo in the exponent of the mass term in the latter.
2.2. Population synthesis models
The LEdd corresponding to characteristic masses of compact objects in X-ray binaries may manifest as breaks in XLFs (e.g., Kaaret et al. 2017). Moreover, beaming “carves” the XLFs near these limits and extends them, by shifting the portion of the population that is beamed towards the line of sight to higher luminosities, while concealing the rest. As a result, beaming prescriptions can be tested at the population level by comparing population synthesis models with observed XLFs in star-forming galaxies (all PULXs have been found in spiral galaxies; King et al. 2023).
Different codes and choices of stellar evolution parameters can influence the NS/BH ratio, mass-transfer rates, and so on, leading to varying XLF predictions. Here, our goal is not to constrain these parameters, but, rather, to explore the effects of beaming and LEdd, B, while ensuring that the results are not an artifact of the specific modelling choices. For this reason, we employed two drastically different approaches: (i) a parametric binary population synthesis code, COSMIC v.3.4.17 (Breivik et al. 2020), using the default stellar evolution parameters, and (ii) POSYDON v.1 (Fragos et al. 2023), which incorporates up-to-date physics and detailed stellar tracks with MESA (Paxton et al. 2011), using parameters reproducing the XLF (cf., model 44 in Misra et al. 2023, 2024). We evolved 107 massive binaries in a constant 100 Myr star-formation scenario and selected systems with Ṁtr larger than 1% of the classical LEdd to ensure that the full ULX population would be included in the samples (including sub-Eddington ULXs with massive BHs). Focusing on the shape, rather than the normalisation, of the XLFs, we scaled the populations to match the measured scaling of ULXs with star formation rate (∼0.5 ULXs per 1 M⊙ yr−1; Kovlakas et al. 2020; Lehmer et al. 2021). Since POSYDON does not evolve the magnetic field of NSs, we sampled B values from the resulting distribution in the COSMIC population: log(B/1 G) ∼ 𝒩(12.22, 0.64) with a maximum at 13.79. This distribution is consistent with the expectation that PULXs are high-mass X-ray binaries with ages that are shorter than the B-decay timescale (e.g., Revnivtsev & Mereghetti 2016).
3. Results
In the left panels of Fig. 1, we show the Liso (upper panel) and b (lower panel) as a function of the Ṁtr, for M1 = 1.4, and various values of B12. We omit showing the effect of NS mass as it is negligible given its small range (∼1 − 2 M⊙). For B12 = 0.5, the results are numerically equivalent to using the classical LEdd, as the B dependence is activated for B12 > 0.6 (Eq. (5)). We find that NS-ULXs with moderately high B12 = 10 can reach luminosities up to 1041 erg s−1 with mild beaming (> 0.1). Without beaming (dashed lines), significantly higher B12 is necessary to account for NS-ULXs with Liso ≈ 1041 erg s−1.
 |
Fig. 1. Effects of beaming and LEdd, B for a 1.4 M⊙ NS of varying B (see coloured text) on the apparent luminosity Liso (upper left), with and without beaming (solid and dotted lines, respectively), and b (bottom left) as a function of the Ṁtr. We also compare the |
In Eq. (11), Ṁ is the accretion rate at RM, making RM and Ṁ co-dependent. Therefore, they cannot be calculated without an exact knowledge of the accretion geometry; thus, they can only be constrained via measurements of 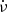 and B. However, we can estimate a conservative range for
and B. However, we can estimate a conservative range for 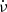 considering Ṁ values between ṀEdd (the minimum rate for a super-Eddington NS) and Ṁtr (the case where all transferred mass is accreted). The right panels of Fig. 1 depict these ranges for M1 = 1.4 and various values of B12, considering the B-dependent (upper) and the classical LEdd (lower). In both cases, the regions do not include spin-up rates corresponding to the propeller regime; that is, RM is less than the corotation radius adopting the fastest spin observed in PULXs (0.42 s; Fürst et al. 2016) to remain conservative. The points are the measured values from PULXs taken from King & Lasota (2019) and lie within the regions defined by the model using both prescriptions of LEdd.
considering Ṁ values between ṀEdd (the minimum rate for a super-Eddington NS) and Ṁtr (the case where all transferred mass is accreted). The right panels of Fig. 1 depict these ranges for M1 = 1.4 and various values of B12, considering the B-dependent (upper) and the classical LEdd (lower). In both cases, the regions do not include spin-up rates corresponding to the propeller regime; that is, RM is less than the corotation radius adopting the fastest spin observed in PULXs (0.42 s; Fürst et al. 2016) to remain conservative. The points are the measured values from PULXs taken from King & Lasota (2019) and lie within the regions defined by the model using both prescriptions of LEdd.
In Fig. 2, we present the synthetic XLFs, incorporating both BH and NS-ULXs. Employing the B-dependent LEdd, B (blue lines), instead of the classical LEdd (green lines), enhances the contribution of NS-ULXs. This is attributed to the reduced b, which reveals a larger fraction of the systems. The increased presence of NS-ULXs improves the agreement with the observations, despite the difference between the COSMIC and POSYDON, particularly in the slope at the less-constrained > 1040 erg s−1 regime, where additional processes might be at play (e.g., neutrino energy loss Mushtukov et al. 2018).
 |
Fig. 2. Synthetic X-ray luminosity functions using COSMIC (left) and POSYDON (right), in the case of no beaming (red dashed), and beaming with the traditional (green), or modified Eddington limit (blue). The populations include both BH and NS-ULXs, compared against observational constraints from the XLF fit of Lehmer et al. (2021, see L21 in the legend) for nearby solar-metallicity star-forming galaxies (black), and ULX demographic data (open circles) from Kovlakas et al. (2020, see K20 in the legend) using larger galaxy samples (Kovlakas et al. 2021). |
In the left panel of Fig. 3, we compare the beaming factors of NS-ULXs (Liso ∈ [1039, 1042 erg s−1) for the classical (green) and B-dependent LEdd (blue), both of the total (dashed curves) and the observed (weighted by b; solid curves) synthetic populations. The classical LEdd implies a highly beamed total population, with a moderately beamed (b ∼ 0.1 − 0.5) observed subpopulation with luminosities in the 1039 − 1040 erg s−1 range (cf. Fig. 1). In contrast, the use of LEdd, B results in more diverse populations. About half of NS-ULXs are moderately beamed (b ∼ 0.05 − 0.5), with the rest representing the majority of the observed population with mild beaming (b > 0.7) and luminosities spanning the full range of PULXs for B12 ∼ 0.5 − 10 (cf. Fig. 1).
 |
Fig. 3. Kernel density estimates (scaled to unity for visibility) of the beaming factor (left) and mechanical feedback (right) in the total (dashed) and observed (solid) population of NS-ULXs from the POSYDON model, using the classical (green) or modified Eddington limit (blue). |
The order-of-magnitude estimate for the kinetic power of outflows in NS-ULXs can reach up to 1042 erg s−1. Depending mainly on the Ṁtr, it is not affected by the LEdd prescription for the total population (dashed lines in Fig. 3; right panel). However, when we account for the observed fraction of NS-ULXs (not beamed out of the line of sight), the distribution of Lkin shifts downward by one and two orders of magnitude using the LEdd, B and LEdd, respectively.
4. Discussion
The increased Eddington limit, LEdd, B allows for both sub- and super-Eddington NS-ULXs without beaming, as well as super-Eddington NS-ULXs with milder beaming as B increases (see Appendix A for practical limits and formulæ). This contrasts with the classical LEdd leading to all NS-ULXs being strongly beamed. Interestingly, sub-Eddington NS accretors do not need to exhibit B12 ≳ 100 to explain the PULX luminosities, since for LEdd, B = 1039 − 1041 erg s−1, we have B12 ∼ 2 − 70.
The effect of the magnetic field in the critical luminosity of NS-ULXs enhances their contribution in the XLFs and helps smooth out prominent breaks (e.g., Kaaret et al. 2017), offering a better match with observed XLFs (e.g., Lehmer et al. 2021) and ULX demographics (e.g., Kovlakas et al. 2020). This has been achieved with magnetic fields in the observed range of X-ray binaries (B12 ∼ 0.1 − 10). However, since our modelling focuses on the general properties of NS-ULXs and the effects on the XLFs, we did not exclude the possibility of multi-polar component magnetic fields that might be required to explain all observables in individual PULXs (e.g., Israel et al. 2017).
The inferred mechanical power of Lkin ≈ 1.3 × 1041 erg s−1 for the nebula near NGC 5907 ULX-1 (Belfiore et al. 2020) is comparable to the apparent ULX luminosity. This often serves as an argument against beaming, however, it remains uncertain whether the mechanical power must be similar to the bolometric luminosity. Our order-of-magnitude estimates of Lkin can reach even higher values, provided high Ṁtr values, independently of beaming. More importantly, using the classical LEdd leads to small b, which makes it unlikely to find NS-ULXs close to wind-powered nebulæ. This is evident from the shift of two orders of magnitude in the total and observed distribution in Fig. 3. Conversely, the lower b in the modified LEdd, B results in a shift of only one order of magnitude, increasing the chances of observing such systems as NGC 5907 ULX-1. Systematic searches of wind-powered nebulæ, with or without the detection of the PULXs powering them, can help achieve a measurement for this shift and put constraints on beaming and outflow models of PULXs.
Using the classical LEdd results in a range of 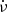 values that just covers the observed values (Fig. 1; lower right), with half of them indicating spin-up rates close to the maximum possible for B12 ≲ 10. This requires either extreme B values or calls for the majority of the transferred mass to reach the magnetospheric radius (Ṁ ≈ Ṁtr), potentially leading to reduced outflows. In this analysis, we neglected disk-star coupling that might introduce additional angular momentum losses, thereby further reducing the spin-up rate. On the other hand, the B-dependent LEdd, B reduces the ṁ, shifting both the apparent luminosities and the locus of super-Eddington sources in the diagram, resulting in a broader range of spin-up rates. In this scenario, NS-ULXs may exhibit a wider variety of spin-up behaviours, with moderate B. Discovery of PULXs with higher spin-up rates could rule out the classical LEdd scenario.
values that just covers the observed values (Fig. 1; lower right), with half of them indicating spin-up rates close to the maximum possible for B12 ≲ 10. This requires either extreme B values or calls for the majority of the transferred mass to reach the magnetospheric radius (Ṁ ≈ Ṁtr), potentially leading to reduced outflows. In this analysis, we neglected disk-star coupling that might introduce additional angular momentum losses, thereby further reducing the spin-up rate. On the other hand, the B-dependent LEdd, B reduces the ṁ, shifting both the apparent luminosities and the locus of super-Eddington sources in the diagram, resulting in a broader range of spin-up rates. In this scenario, NS-ULXs may exhibit a wider variety of spin-up behaviours, with moderate B. Discovery of PULXs with higher spin-up rates could rule out the classical LEdd scenario.
We highlight the importance of incorporating a more detailed treatment of the effects of magnetic fields in NS-ULXs, especially with respect to the LEdd. In working towards a self-consistent framework of NS-ULXs, we need parameter studies (investigating kick velocity distributions, mass-transfer prescriptions; e.g., El Mellah et al. 2019, and other properties) with population synthesis codes integrating results from magnetospheric accretion simulations. The latter can provide more realistic prescriptions for the bolometric luminosity and b in NS-ULXs (e.g., Vasilopoulos et al. 2021), which are often extrapolated (e.g., Wiktorowicz et al. 2019; Misra et al. 2024) from the BH-ULX population (King 2009), although they are expected to be qualitatively similar (e.g., King et al. 2023). Furthermore, the dependence of RM and Ṁ(RM) (e.g., Chashkina et al. 2017) as well as that of the critical luminosity (see Mushtukov et al. 2015; Brice et al. 2021 for dipolar and multipolar fields, respectively) on the accretion geometry points at the need for prescriptions that are applicable to population synthesis models. Despite important efforts contributing to our understanding of accretion in NS-ULXs (e.g., Kuranov et al. 2020; Mushtukov et al. 2024), the effect of B in LEdd in simulations of highly magnetised NSs remains poorly explored (see discussion in Inoue et al. 2024). In the present work, we show that this effect leads to markedly different results at the population level, even in the case where the BH-ULX prescriptions are broadly valid.
The above-mentioned improvements will enable future population synthesis codes to self-consistently model mass transfer and angular momentum loss (e.g., Misra et al. 2020), NS spin-up and disk-star coupling (e.g., Kluźniak & Rappaport 2007), and orbital evolution (e.g., Chen 2024), as well as emission and the detectability of pulsations (e.g., King & Lasota 2020). This is necessary to test models using all available data from individual ULXs and PULXs, at the population level.
Acknowledgments
We thank the anonymous referee for their valuable comments and suggestions, which have significantly improved the quality of this manuscript. KK is supported by a fellowship program at the Institute of Space Sciences (ICE-CSIC) funded by the program Unidad de Excelencia María de Maeztu CEX2020-001058-M. DM acknowledges that this project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 101002352, PI: M. Linares). RA and GLI acknowledge financial support from INAF through grant “INAF-Astronomy Fellowships in Italy 2022 – (GOG)”. GLI also acknowledges support from PRIN MUR SEAWIND (2022Y2T94C), which was funded by NextGenerationEU and INAF Grant BLOSSOM.
References
- Abarca, D., Parfrey, K., & Kluźniak, W. 2021, ApJ, 917, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Heida, M., Maccarone, T., et al. 2022, ApJ, 937, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [Google Scholar]
- Belfiore, A., Esposito, P., Pintore, F., et al. 2020, Nat. Astron., 4, 147 [Google Scholar]
- Beloborodov, A. M. 1998, MNRAS, 297, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Breivik, K., Coughlin, S., Zevin, M., et al. 2020, ApJ, 898, 71 [Google Scholar]
- Brice, N., Zane, S., Turolla, R., & Wu, K. 2021, MNRAS, 504, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Brightman, M., Harrison, F. A., Fürst, F., et al. 2018, Nat. Astron., 2, 312 [CrossRef] [Google Scholar]
- Chashkina, A., Abolmasov, P., & Poutanen, J. 2017, MNRAS, 470, 2799 [Google Scholar]
- Chashkina, A., Lipunova, G., Abolmasov, P., & Poutanen, J. 2019, A&A, 626, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W.-C. 2024, ApJ, 973, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Dall’Osso, S., Perna, R., & Stella, L. 2015, MNRAS, 449, 2144 [CrossRef] [Google Scholar]
- Eksi, K. Y., Andac, I. C., Cikintoglu, S., et al. 2015, MNRAS, 448, L40 [CrossRef] [Google Scholar]
- El Mellah, I., Sundqvist, J. O., & Keppens, R. 2019, A&A, 622, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erkut, M. H., Türkoğlu, M. M., Ekşi, K. Y., & Alpar, M. A. 2020, ApJ, 899, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 2002, Accretion Power in Astrophysics, 3rd edn. (Cambridge University Press) [Google Scholar]
- Fürst, F., Walton, D. J., Harrison, F. A., et al. 2016, ApJ, 831, L14 [Google Scholar]
- Herold, H. 1979, Phys. Rev. D, 19, 2868 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A., Ohsuga, K., Takahashi, H. R., & Asahina, Y. 2023, ApJ, 952, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A., Ohsuga, K., Takahashi, H. R., Asahina, Y., & Middleton, M. J. 2024, ApJ, 977, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- King, A. R. 2009, MNRAS, 393, L41 [NASA ADS] [Google Scholar]
- King, A., & Lasota, J.-P. 2019, MNRAS, 485, 3588 [Google Scholar]
- King, A., & Lasota, J.-P. 2020, MNRAS, 494, 3611 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Lasota, J. P. 2021, arXiv e-prints [arXiv:2112.03779] [Google Scholar]
- King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., Lasota, J.-P., & Kluźniak, W. 2017, MNRAS, 468, L59 [Google Scholar]
- King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672 [CrossRef] [Google Scholar]
- Kluźniak, W., & Rappaport, S. 2007, ApJ, 671, 1990 [CrossRef] [Google Scholar]
- Kovlakas, K., Zezas, A., Andrews, J. J., et al. 2020, MNRAS, 498, 4790 [Google Scholar]
- Kovlakas, K., Zezas, A., Andrews, J. J., et al. 2021, MNRAS, 506, 1896 [NASA ADS] [CrossRef] [Google Scholar]
- Kovlakas, K., Fragos, T., Schaerer, D., & Mesinger, A. 2022, A&A, 665, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuranov, A. G., Postnov, K. A., & Yungelson, L. R. 2020, Astron. Lett., 46, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Lasota, J.-P., & King, A. 2023, MNRAS, 526, 2506 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmer, B. D., Eufrasio, R. T., Basu-Zych, A., et al. 2021, ApJ, 907, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lipunova, G. V. 1999, Astron. Lett., 25, 508 [NASA ADS] [Google Scholar]
- Liu, J. 2024, ApJ, 961, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., Brightman, M., Pintore, F., et al. 2019, MNRAS, 486, 2 [Google Scholar]
- Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
- Misra, D., Fragos, T., Tauris, T. M., Zapartas, E., & Aguilera-Dena, D. R. 2020, A&A, 642, A174 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misra, D., Kovlakas, K., Fragos, T., et al. 2023, A&A, 672, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misra, D., Kovlakas, K., Fragos, T., et al. 2024, A&A, 682, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mushtukov, A. A., & Portegies Zwart, S. 2023, MNRAS, 518, 5457 [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Poutanen, J. 2015, MNRAS, 454, 2539 [Google Scholar]
- Mushtukov, A. A., Tsygankov, S. S., Suleimanov, V. F., & Poutanen, J. 2018, MNRAS, 476, 2867 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Ingram, A., Middleton, M., Nagirner, D. I., & van der Klis, M. 2019, MNRAS, 484, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Portegies Zwart, S., Tsygankov, S. S., Nagirner, D. I., & Poutanen, J. 2021, MNRAS, 501, 2424 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Ingram, A., Suleimanov, V. F., et al. 2024, MNRAS, 530, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1992, Acta Astron., 42, 145 [NASA ADS] [Google Scholar]
- Pakull, M. W., & Mirioni, L. 2002, arXiv e-prints, [arXiv:astro-ph/0202488] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Pinto, C., Middleton, M. J., & Fabian, A. C. 2016, Nature, 533, 64 [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., & Mereghetti, S. 2016, in The Strongest Magnetic Fields in the Universe, eds. V. Beskin, A. Balogh, M. Falanga, et al. (New York, NY: Springer New York), 299 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black holes, white dwarfs and neutron stars. The physics of compact objects (John Wiley& Sons, Ltd) [CrossRef] [Google Scholar]
- Vasilopoulos, G., Koliopanos, F., Haberl, F., et al. 2021, ApJ, 909, 50 [Google Scholar]
- Walton, D. J., Bachetti, M., Fürst, F., et al. 2018, ApJ, 857, L3 [Google Scholar]
- Wiktorowicz, G., Lasota, J.-P., Middleton, M., & Belczynski, K. 2019, ApJ, 875, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Zezas, A., Fabbiano, G., Rots, A. H., & Murray, S. S. 2002, ApJ, 577, 710 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Analytical formulæ
Using Eqs. (1)-(6), we provide practical limits and formulæ for observed sources under the case of canonical NS mass (1.4 M⊙) and radius (106 cm). If there is evidence of beaming, then for B12 < 0.6, ULX luminosities require b < 0.6. This limit increases with B until B12 ≈ 0.9 where b approaches unity. In the weak B case, the beaming factor can be constrained by the apparent luminosity (solving eq. 6 in Kovlakas et al. 2022 for b):
Evidence of beaming exceeding this value (bmin < b < 1) can be used to estimate the B:
whereas, lack of beaming puts a lower limit on the B,
All Figures
 |
Fig. 1. Effects of beaming and LEdd, B for a 1.4 M⊙ NS of varying B (see coloured text) on the apparent luminosity Liso (upper left), with and without beaming (solid and dotted lines, respectively), and b (bottom left) as a function of the Ṁtr. We also compare the |
| In the text | |
 |
Fig. 2. Synthetic X-ray luminosity functions using COSMIC (left) and POSYDON (right), in the case of no beaming (red dashed), and beaming with the traditional (green), or modified Eddington limit (blue). The populations include both BH and NS-ULXs, compared against observational constraints from the XLF fit of Lehmer et al. (2021, see L21 in the legend) for nearby solar-metallicity star-forming galaxies (black), and ULX demographic data (open circles) from Kovlakas et al. (2020, see K20 in the legend) using larger galaxy samples (Kovlakas et al. 2021). |
| In the text | |
 |
Fig. 3. Kernel density estimates (scaled to unity for visibility) of the beaming factor (left) and mechanical feedback (right) in the total (dashed) and observed (solid) population of NS-ULXs from the POSYDON model, using the classical (green) or modified Eddington limit (blue). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



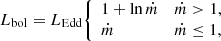
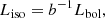
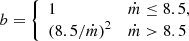
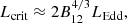
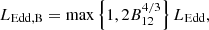
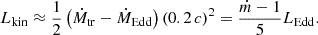
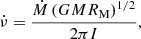
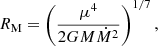
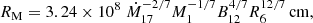
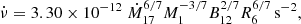
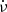
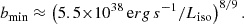
![$$ \begin{aligned} B_{12} =\left[\dfrac{ b L_{\rm iso} }{3.5{\times }10^{38}\,\mathrm{erg\,s^{-1}}\left(3.14+\ln b^{-1/2}\right)} \right]^{3/4}, \end{aligned} $$](/articles/aa/full_html/2025/02/aa53274-24/aa53274-24-eq19.gif)