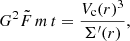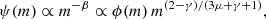| Issue |
A&A
Volume 695, March 2025
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202452393 | |
| Published online | 11 March 2025 | |
Growth of massive black holes in FFB galaxies at cosmic dawn
1
Racah Institute of Physics, The Hebrew University, Jerusalem 91904, Israel
2
SCIPP, University of California, Santa Cruz, CA 95064, USA
3
Department of Astronomy, Yale University, New Haven, CT 06520, USA
⋆ Corresponding author; dekel@huji.ac.il
Received:
27
September
2024
Accepted:
3
February
2025
Aims. The scenario of feedback-free starbursts (FFB), which predicts excessively bright galaxies at cosmic dawn as observed using JWST, may provide a natural setting for black hole (BH) growth. This involves the formation of intermediate-mass seed BHs and their runaway mergers into super-massive BHs with high BH-to-stellar mass ratios and low Active Galactic Nucleus (AGN) luminosities.
Methods. We present a scenario of merger-driven BH growth in FFB galaxies and study its feasibility.
Results. Black hole seeds form within the building blocks of the FFB galaxies, namely, thousands of compact star clusters, each starbursting in a free-fall time of a few million years before the onset of stellar and supernova feedback. The BH seeds form by rapid core collapse in the FFB clusters, in a few free-fall times, which is sped up by the migration of massive stars due to the young, broad stellar mass function and stimulated by a “gravo-gyro” instability due to internal cluster rotation and flattening. BHs of ∼104 M⊙ are expected in ∼106 M⊙ FFB clusters within sub-kiloparsec galactic disks at z ∼ 10. The BHs then migrate to the galaxy center by dynamical friction, hastened by the compact FFB stellar galactic disk configuration. Efficient mergers of the BH seeds will produce ∼106 − 8 M⊙ BHs with a BH-to-stellar mass ratio ∼0.01 by z ∼ 4 − 7, as observed. The growth of the central BH by mergers can overcome the bottleneck introduced by gravitational wave recoils if the BHs inspiral within a relatively cold disk or if the escape velocity from the galaxy is boosted by a wet compaction event. Such events, common in massive galaxies at high redshifts, can also help by speeding up the inward BH migration and by providing central gas to assist with the final parsec problem.
Conclusions. The cold disk version of the FFB scenario provides a feasible route for the formation of supermassive BHs.
Key words: galaxies: evolution / galaxies: formation
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The largest supermassive black holes (SMBHs) observed at high redshifts have long posed a challenge for simple models of SMBH formation and evolution. The observed high-z SMBHs with mass ≳109 M⊙ (Barth et al. 2003; Mortlock et al. 2011; Bañados et al. 2016) are too massive to have grown from Eddington-limited accretion onto stellar-mass black hole (BH) seeds (Haiman & Loeb 2001), suggesting that some exotic process must have quickly assembled intermediate-mass BH seeds in the early Universe (Volonteri 2010). The three most commonly discussed scenarios are, in increasing order of seed mass, (i) Pop III stellar remnants (Schneider et al. 2002), (ii) runaway collisions in dense star clusters (Portegies Zwart et al. 2004), and (iii) direct collapse of low-metallicity gas clouds (Loeb & Rasio 1994). At present, it is not clear which, if any, of these scenarios is responsible for the most extreme high-z SMBHs (Inayoshi et al. 2020).
More recently, a second puzzle has emerged concerning the high-z SMBH formation and evolution. JWST observations at z = 4 − 7 from the CEERS and JADES surveys (Harikane et al. 2023; Maiolino et al. 2024b; Übler et al. 2023) indicate SMBHs of masses in the range 107 ± 1 M⊙ with especially high BH-to-stellar mass ratios, fbh, in the ball park of fbh ∼ 0.01. A statistical analysis by Pacucci et al. (2023), based on a relatively uniform subsample of 21 massive BHs and their host galaxies, has yielded a bias-corrected BH-to-stellar mass relation that is ten to 100 times above the standard relation at low redshifts (e.g. Reines & Volonteri 2015), indicating a deviation larger than 3σ between the two. While an alternative statistical analysis of these data by Li et al. (2024a) cautions that the difference between the relations at high and low redshifts may be less dramatic, the evidence for a high fbh at high redshifts is intriguing, and it calls for a theoretical understanding.
We investigate here how such SMBHs may naturally arise within the scenario of “feedback-free starbursts” (FFB) (Dekel et al. 2023a; Li et al. 2024b), which predicts excessively bright galaxies at cosmic dawn as observed using JWST. This physical model envisions high star-formation efficiency in free-fall collapses of thousands of dense gas clouds within compact galaxies, and thus explains the JWST-observed excess of bright galaxies at z ∼ 10 compared to the standard theory that is valid at later epochs, where stellar feedback suppresses star formation. At first glance, the extreme efficiency of FFB star formation may seem to be in competition with the need for efficient BH formation and a high fbh, but we argue that the FFB scenario can actually provide a natural setting for the SMBH challenge. Our current analysis is meant as a feasibility study aimed at verifying the conditions under which FFB galaxy formation at cosmic dawn can enable the formation of SMBHs with a high fbh ratio by z = 4 − 7 and to what extent the SMBH growth can be driven by BH mergers.
We address four crucial stages in the BH growth process. First is the formation of intermediate-mass seed BHs by sped-up “core collapse” (Lynden-Bell & Wood 1968) within the FFB star clusters at cosmic dawn. The second stage is the subsequent inward migration of these BHs within the FFB disk galaxies by dynamical friction (DF) (Chandrasekhar 1943) against the stars and dark matter in the compact galaxies. Third is overcoming a bottleneck in the initial growth of the SMBHs subject to gravitational-wave (GW) recoils after BH mergers (Pretorius 2005; Campanelli et al. 2006; Baker et al. 2006). The fourth stage involves the effects of “wet compaction” events (Zolotov et al. 2015; Lapiner et al. 2023) on avoiding possible dynamical-friction stalling at the end of the second stage’s DF-driven inspiral (Read et al. 2006; Kaur & Sridhar 2018; Banik & van den Bosch 2021), on preventing escape by recoils in the third stage (Madau & Quataert 2004; Blecha & Loeb 2008), and in helping with a viscous last parsec approach (Begelman et al. 1980).
The building blocks of an FFB galaxy are thousands of young star clusters, each formed in a feedback-free starburst during a free-fall time of a few million years. Such clusters are expected to develop core collapse, driven by two-body star-star relaxation, and may under certain conditions form massive central stellar objects that soon after collapse to seed BHs (Spitzer & Hart 1971; Portegies Zwart et al. 2004; Devecchi & Volonteri 2009; Katz et al. 2015; Rantala et al. 2024). In order to produce massive seed BHs with a high fbh, the core collapse should occur in less than ∼3 Myr, which is the characteristic lifetime of the massive stars (Hirschi 2007). During that period, the core collapse is enhanced by the mass segregation associated with the presence of the massive stars, and the BH growth is not suppressed by supernova and stellar feedback. The core collapse can be sped up by three special features of the FFB clusters, namely, their compactness, the presence of young massive stars in them, and their internal rotation and spatial flattening.
Compactness is the basic feature of the FFB clusters at cosmic dawn. They are expected to have an internal 3D density of n ∼ ncrit ∼ 3 × 103 cm−3, which allows free-fall collapse before the onset of feedback as well as cooling below 104 K during the free fall (Dekel et al. 2023a). The clusters are also expected to have a surface density of Σ ∼ Σcrit ∼ 3 × 103 M⊙ pc−2 such that they are gravitationally confined against outflows by radiative feedback (Menon et al. 2023; Grudić & Hopkins 2023).
Core collapse is sped up by mass segregation, that is the inward migration of young massive stars, which are naturally present during the feedback-free period of ∼3 Myr. The high-z initial stellar mass function (IMF) is rather uncertain and could differ from the standard IMF at lower redshifts. In particular, it may be top heavy, possibly made of pop-III stars (Bromm et al. 2002) or a later population as obtained in certain simulations (Grudić & Hopkins 2023; Bate 2023) and as argued based on certain observations (Cameron et al. 2024; Steinhardt et al. 2023), though these interpretations are controversial (Tacchella et al. 2024). A top-heavy IMF with an enhanced UV luminosity-to-stellar mass ratio of a few to ten will also add to the excessive brightness as observed by JWST (Yung et al. 2024) but it will not suppress the feedback-free high star formation efficiency (Menon et al. 2024). Such a top-heavy IMF, with a larger fraction of massive stars, should help speed up the core collapse.
Star-star interactions would be boosted if the clusters are spatially flattened, and the core collapse would be sped up further when the clusters are rotating, giving rise to a “gravo-gyro” instability (Hachisu 1979). This would be natural in the disk version of the FFB scenario (Dekel et al. 2023a), where the star-forming clouds, of ∼107 M⊙ and below, fragment from Toomre-unstable rotating gaseous galactic disks (Toomre 1964; Dekel et al. 2009). Indeed, clumps formed in this way are expected to be largely supported by rotation and to be flattened correspondingly (Ceverino et al. 2012).
After estimating the core-collapse time and the resultant BH seed mass as a function of the cluster mass and radius, its flattening and rotation support, and the IMF in it, we will evaluate the range of FFB clump properties that permit core collapse as rapid as 3 Myr. This will allow us to estimate the population of seed BHs produced during the FFB phase at cosmic dawn, and predict the corresponding fbh in these clusters. We estimate below that BH seeds of ∼104 M⊙ can typically form in ∼106 M⊙ clusters within the FFB disks at z ∼ 10.
Following the z ∼ 10 FFB phase of a galaxy, the system of thousands of star clusters with their central seed BHs is expected to evolve within the compact galactic disk of radius ∼200 pc (Li et al. 2024b, and references therein). The clusters of internal velocities ∼10 km s−1, orbiting in a potential well of ∼100 km s−1, are expected to tidally disrupt each other in a few orbital times to form a centrally concentrated galactic stellar disk within a common dark-matter halo. Subsequently, the seed BHs (and any surviving clusters) are expected to migrate toward the galaxy center by dynamical friction, where they could coalesce into a SMBH. In order to produce massive SMBHs with high values of fbh by z ∼ 4 − 7, as observed, most of the seed BHs should migrate to the center in less than a gigayear. Such an efficient dynamical friction would require large enough BH seed masses, and it would benefit from the compact, high density galactic FFB configuration. The DF is expected to be particularly efficient in the disk version of the FFB scenario, where the relative velocities of the orbiting BHs and the surrounding stars are low, especially if the profiles of density and angular velocity are steeply declining with radius to avoid DF core stalling. We will evaluate the expected migration timescales in FFB galaxies and verify the conditions for the required efficient inward migration.
A bottleneck in the initial growth of the SMBH by BH mergers could be caused by the GW recoils of the merger remnants (e.g., as simulated by Sijacki et al. 2009). For major mergers of mass ratios between 0.1 and 0.8, the recoil velocity, as computed by numerical general relativity, could be larger than the central escape velocity from the galaxy, especially in cases of BH spin-orbit misalignments. The FFB galaxies, being both massive and compact, are expected to provide relatively high, confining escape velocities. However, the spin-orbit alignments necessary for non-ejective recoils would require that the seed BHs be inspiraling through a rather cold galactic disk configuration. We will quantify the conditions for overcoming this recoil bottleneck.
SMBH growth in the last two stages can be boosted by events of wet compaction into baryon-dominated ‘nuggets’. As seen in simulations (Zolotov et al. 2015; Lapiner et al. 2023; de Graaff et al. 2025) and as observed (Barro et al. 2013, 2017; van Dokkum et al. 2015; Huertas-Company et al. 2018; de Graaff et al. 2025), this process is generic in the high-z history of galaxies, preferably when the DM halo exceeds a ‘golden mass’ of ∼1011.5 M⊙ (Dekel et al. 2019). It has far-reaching implications on all major galaxy properties (Tacchella et al. 2016a,b; Tomassetti et al. 2016; Lapiner et al. 2023). Triggered by drastic angular-momentum loss, for example due to wet galaxy mergers or collisions of counter-rotating inflowing streams, gas is pushed to the central regions of the galaxies. This results in a cuspy gas-rich ‘blue nugget’ that passively evolves to a compact stellar ‘red nugget’, allowing the formation of a stable, extended gaseous disk/ring around it (Dekel et al. 2020).
Such compaction events may assist SMBH growth by (i) enhancing DF migration of the BH seeds, which is of special importance when the original galaxy structure may cause “core stalling”; (ii) increasing the escape velocity of the host galaxy, which helps to retain BH merger products against GW recoil; and (iii) providing central gas to help solve the final parsec problem.
The outline of this article is as follows. In Sect. 3 we estimate the seed BH population formed by core collapse in the FFB star clusters at cosmic dawn. In Sect. 4 we evaluate the inward migration of the BHs and the expected SMBH mass and fbh at z ∼ 4 − 7. In Sect. 5 we evaluate the potential effect of GW recoil of the SMBH at the early phases of SMBH growth. In Sect. 6 we address the possible assistance to SMBH growth by compaction events. Finally, in Sect. 7 we summarize our conclusions.
2. Observed black hole-stellar mass relation
Black-hole masses and their host stellar masses have been estimated for galaxies with low-luminosity AGN from the CEERS, JADES and GA-NIFS surveys using JWST in the redshift range z = 4 − 7 (Harikane et al. 2023; Maiolino et al. 2024b; Übler et al. 2023). These black holes are likely only the tip of the iceberg, and the derived BH-to-stellar mass relation has to be bias-corrected for the coupled effects of selection biases and the ∼1 dex measurement uncertainties in both the BH and stellar masses. Pacucci et al. (2023) performed a statistical analysis of a relatively uniform sample of 21 AGN from these surveys of massive BHs, eight from Harikane et al. (2023), twelve from Maiolino et al. (2024b) and one from Übler et al. (2023). These are all spectroscopically confirmed with NIRSpec, their black hole masses are estimated with the Hα line, their host stellar masses are estimated by UV to optical SED fitting, and lensed objects or double AGN candidates were not included. They obtained at z = 4 − 7 the bias-corrected relation
with a scatter of 0.69 dex. In comparison, the standard local relation, obtained by Reines & Volonteri (2015) using more massive galaxies at low redshifts, is of a similar functional form with the numerical coefficients −4.10(± 0.08) and 1.05(± 0.11) respectively. Pacucci et al. (2023) estimate a deviation larger than 3σ between these relations, with the values of fbh at z = 4 − 7 on average higher than the local relation by a factor of 10–100. The data points and the bias-corrected fbh ratios are shown in Fig. 1, based on Pacucci et al. (2023), with additional data by Mezcua et al. (2024) at z = 1 − 3. The origin of this discrepancy is a major open issue.
 |
Fig. 1. Black hole mass versus stellar mass as estimated from observations. Shown is the bias-corrected relation at z = 4 − 7 as derived by Pacucci et al. (2023) (red shading, ±1σ scatter). It is based on the data from JWST marked by the symbols (JADES, CEERS and GA-NIFS Maiolino et al. 2024b; Harikane et al. 2023; Übler et al. 2023). Also shown are data at z = 1 − 3 (Mezcua et al. 2024). The high-z relation is compared to the local relation by Reines & Volonteri (2015) (green shading). The typical values of fbh at z = 4 − 7 are higher than the local relation by > 3σ, a factor of 10 − 100. |
We note in passing that even more extreme cases are detected, at higher redshift and/or with a very high fbh, such as UHZ1 at z = 10.1 with fbh of order unity (Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024a; Natarajan et al. 2024). In the current feasibility study we focus on the origin of the average properties of the main body of massive BHs at z ∼ 4 − 7, and comment on the possible origin of scatter about the mean relation.
3. Black hole seeds in FFB star clusters
Given the efficient star formation in FFB star clusters at cosmic dawn, one might suspect that it would come at the expense of BH growth in these clusters. We show here that, quite the contrary, the FFB clusters are likely to provide an ideal setting for the formation of intermediate-mass black holes (IMBH), and attempt to characterize the population of IMBHs that are expected to form by core collapse in the FFB clusters.
3.1. Core collapse in a young cluster with a broad IMF
Stellar clusters are expected to suffer core collapse due to two-body relaxation that induces gravo-thermal instability (Lynden-Bell & Wood 1968). In this case, energy transfer from a kinematically hot gravitating core to the cooler outer envelope makes the core contract and heat up further due to the virial theorem (or the associated negative heat capacity of gravitating systems), leading to a runaway process. This leads to a very massive central star (VMS) (Portegies Zwart et al. 1999) which collapses to a black hole that may contain as much as one percent of the cluster mass (Yungelson et al. 2008; Portegies Zwart & McMillan 2002; Heger et al. 2003; Rantala et al. 2024; Fujii et al. 2024). In a cluster younger than a few Myr, when the massive stars are still alive on the main sequence, the core collapse is significantly sped up by the inward migration of the massive stars due to mass segregation. Thus, in order to efficiently form a massive seed BH at the center of the cluster, the core collapse should occur in less than ∼3 Myr, the main-sequence lifetime of massive stars of ∼40 M⊙ (Hirschi 2007). This time is safely before the onset of feedback (Dekel et al. 2023a, Fig. 1) that otherwise might have suppressed the VMS/BH growth. The rapid inward migration of the massive stars, and their disappearance into the VMS/BH while they are still on the main sequence, prevents them from ever generating effective stellar feedback. Thus, the formation of a massive seed BH is intimately related to the FFB phase in the cluster, either as a cause or as an effect. The important quantities to be evaluated are the time for core collapse and the resultant black-hole mass.
Too comments are worth mentioning in passing. First, if the massive stars in the clusters indeed coalesce with the central BHs before they explode as SNe, the feedback from post-FFB clusters would be somewhat weakened, contributed by lower-mass stars. This may enhance the shielding of new FFB clusters beyond the original estimate of Dekel et al. (2023a), who conservatively concluded that the clouds have to be more massive than 104 M⊙ for survival. This could also lower even further the gas fraction, metallicity, dust content and outflow strength in FFB galaxies as evaluated in Li et al. (2024b). On the other hand, encounters between main sequence stars and BHs may produce micro-tidal disruption events (Perets et al. 2016), which can generate ‘accretion feedback’ in the form of radiative luminosity or mechanical luminosity from the ensuing period of super-Eddington accretion driving outflows.
Second, we comment that high values of fbh in massive BHs were predicted as a result of direct gas collapse in nuclear star clusters (NSCs), in a series of papers from Lodato & Natarajan (2006) to Alexander & Natarajan (2014) and Natarajan et al. (2024). In this different picture, the first massive star that collapses into a BH grows initially via wind-fed accretion as it random walks through the star cluster colliding with the stars. The situation in this NSC is essentially free of feedback, partially resembling the FFB conditions that we propose are valid in the thousands of FFB clusters in a massive galaxy at cosmic dawn.
3.1.1. Core collapse time
In a cluster of mass Mc and half-mass radius Re, if it consists of N equal-mass stars, as can be approximated in old globular clusters, the two-body relaxation time is
where γ ∼ 0.11 (Giersz & Heggie 1994). The core-collapse time in this case is rather long, tcc ∼ 15 − 20 trlx. In a multi-mass system, on the other hand, the core collapse occurs on the shorter segregation time, due to energy equipartition or dynamical friction. Based on Spitzer & Hart (1971) and Portegies Zwart et al. (2004), when a standard Kroupa (2001) IMF is assumed, the segregation time can be evaluated by a similar expression to Eq. (2) but with N replaced by Mc/mmax (rather than N = Mc/⟨m⟩), where mmax is the mass of the most massive star in the cluster. This gives a core-collapse time of tcc ∼ 0.2 trlx, which is
Here Λ ≃ γ Mc/mmax, which gives lnΛ ∼ 4.7 for γ = 0.11. This estimate has been crudely confirmed by simulations (Rizzuto et al. 2021; Rantala et al. 2024). It is in the same ball park as the alternative estimate by Portegies Zwart & McMillan (2002) and Devecchi & Volonteri (2009) where the IMF is characterized by ⟨m⟩ rather mmax,
Here the Coulomb logarithm lnΛc ≃ ln(0.1 Mc/⟨m⟩) is with respect to 8.5, the value assumed for Mc = 105.7 M⊙ and ⟨m⟩ = 10 M⊙.
3.1.2. Black hole mass
For low metallicity, the stellar mass loss is small, so the growth of the VMS is efficient. Once the VMS is more massive than 260 M⊙, the resultant black hole is expected to retain most of the mass of the VMS (Heger et al. 2003). According to Portegies Zwart & McMillan (2002), the black hole mass at tcc is expected to be
where m⋆ is the initial mass of the massive star that became the VMS. In the second term there should be a multiplicative factor of order unity which depends on tcc with respect to 3 Myr. For a cluster of Mc ∼ 106 M⊙, this gives Mbh ∼ 104 M⊙. The high seed BH mass is a key for obtaining a high fbh, in the ball park of 0.01, as indicated by the observations.
The black holes formed by core collapse will grow further, over longer timescales, due to the tidal capture and/or disruption of stars (Stone et al. 2017; Rizzuto et al. 2023), and possibly gas accretion as well (Schleicher et al. 2022). Assuming that the long-term intermediate-mass BH growth occurs only after any intra-cluster gas has been depleted or expelled due to stellar feedback, we focus on the the timescale for growth by the first possibility of star capture. Early stages of growth via star capture can occur in the “full loss cone” limit, but once the BH grows modestly, it will generally find itself in the “empty loss cone” regime (Cohn & Kulsrud 1978), where the rate of stellar consumption is limited, and set by the rate at which two-body scatterings diffuse stars onto highly radial orbits that can interact strongly with the BH at pericenter (Stone et al. 2017). Taking the approximate rate of empty loss cone growth to be Ṅ from Eq. (36) of Stone et al. (2017), and assuming that all clusters have the same surface mass density Σ, we find that the mass doubling time for the BH, t2 = Mbh/(⟨ms⟩Ṅ), is roughly
In evaluating Ṅ, we have taken the average stellar mass and radius to be ⟨ms⟩ = 0.3 M⊙ and rs = 0.38 R⊙, respectively. We have also assumed that the cluster half-mass radius is Re = Mc1/2/Σ1/2, and that the second moment of the stellar mass function is ⟨ms2⟩ = 1 M⊙2. Logarithmic factors in Eq. (36) of Stone et al. (2017) have been evaluated assuming the fiducial values for Mbh, Mc, and Σ that normalize Eq. (6) above, introducing mild (logarithmic) inaccuracies when extending this approximate formula for example to other BH masses. However, from this simple formula, combined with the BH mass as a function of cluster mass from Eq. (5), we can see that unless initial cluster masses are relatively large (Mc ≫ 105 M⊙), the initial mass of the BH will not be heavily modified by star capture within a time t ≲ 100 Myr. We have assumed here that, as with tidal disruption events, half of the star’s mass is eventually consumed by the BH (Rees 1988). We note also that this rate of star capture is calculated using a classic empty loss cone formula that does not account for Brownian motion of the BH, an effect which is not well understood but which may become more important in the intermediate-mass range (Magorrian & Tremaine 1999).
A population of growing BHs in FFB star clusters of the same surface density Σ but different masses Mc will achieve a simple, power-law scaling,
This expression assumes that we are considering late enough times so that t > t2, such that Mbh(t) ≃ ⟨ms⟩Ṅ t. It also assumes that the times are late enough so that Mbh ≪ Mc, namely, the BH has not yet consumed the majority of the star cluster, and that the clusters still survive tidal disruption. Assuming a cluster mass function ϕ ∝ Mc−α, Eq. (7) implies a late-time BH mass function within the clusters
at least for lower BH masses and as long as the clusters survive intact. With a mass-function slope α = 1.8 for the clusters (Mandelker et al. 2014, 2017), the slope for the BH mass function could steepen by stellar capture to values as large as δ = 2.75. A conservative version of this steepening will serve our purposes when estimating the effect of GW recoil in Sect. 5.4 below.
Adopting the core-collapse time estimate from Eq. (4), or alternatively from Eq. (3), Fig. 2 shows the relation between cluster mass and half-mass radius for tcc = 3 Myr. This is in comparison to the FFB characteristic quantities within the half-mass radius, namely density n = 103.5 cm−3 and surface density Σ = 103.5 M⊙ pc−2 (Dekel et al. 2023a). FFB clouds of the Jeans mass and radius, ∼106 M⊙ and ∼7 pc (Dekel et al. 2023a), lie above the line of core-collapse in 3 Myr, but not too far away if the IMF is very top heavy, for example, of a population-III.1 type, with ⟨m⟩ ∼ 100 M⊙ in Eq. (4) or mmax > 300 M⊙ in Eq. (3). For a less top heavy IMF, with ⟨m⟩ ∼ 10 M⊙ or mmax ≳ 100 M⊙, the Jeans-mass clouds lie well above the region for tcc < 3 Myr. However, if sub-Jeans clouds form by fragmentation with the same critical surface density Σ that characterizes FFB, they should lie along the Σ = const. red line, such that core collapse will occur for Mc ≤ 105 M⊙ and Re ≤ 2 pc. According to Eq. (5), the black-hole will form in such cluster’s FFB phase with Mbh ∼ 103 M⊙. This is in the intermediate mass range of BHs, but on its relatively low side, possibly not massive enough for inspiraling to the galaxy center in less than a Gigayear, to be estimated in Sect. 4 below.
 |
Fig. 2. Black hole growth in non-rotating FFB clusters with a broad IMF. Shown is the cluster half-mass radius versus mass. The magenta curves and regions below them refer to clusters where core collapse occurs within 3 Myr, the lifetime of massive stars. Left: based on Eq. (4) (Portegies Zwart & McMillan 2002; Devecchi & Volonteri 2009), assuming either ⟨m⟩ = 10 M⊙ (solid) or ⟨m⟩ = 100 M⊙ (dashed). Right: based on Eq. (3) (Rizzuto et al. 2021, Eq. (4)), assuming mmax = 100 (solid) or 300 M⊙ (dashed). The blue and red lines refer to constant density n = 103.5 cm−3 and surface density Σ = 103.5 M⊙ pc−2 within the half-mass radius. Feedback-free starbursts are expected to occur near such densities. FFB clouds of the Jeans mass and radius, ∼106 M⊙ and ∼7 pc, lie above the core-collapse line, though not too far away if the IMF is very top-heavy, of a population-III.1 type, with ⟨m⟩ ∼ 100 M⊙ (left) or mmax > 300 M⊙ (right). If the sub-Jeans clouds form by fragmentation with the same Σ, they should lie along the red line, such that core collapse will occur in 3 Myr for Mc ≤ 105 M⊙ and Re ≤ 2 pc. The corresponding black-hole mass at the end of the FFB phase, Eq. (5), in addition to the initial mass of the massive star that became the VMS, is marked in the top axis, indicating Mbh ∼ 103 M⊙ in ∼105 M⊙ clusters. |
3.2. Rotating clusters: Gravo-gyro instability and flattening
In the disk version of the FFB model, the clumps formed by Toomre disk instability are expected to be largely supported by rotation (Ceverino et al. 2012), and they will be spatially flattened accordingly. This would speed up the core collapse in them due to (i) the gravo-gyro instability (Hachisu 1979, 1982; Ernst et al. 2007; Kim et al. 2008; Hong et al. 2013; Kamlah et al. 2022), and (ii) the flattening which induces a shorter two-body relaxation time and dynamical friction time. Each of these effects could shorten the core-collapse time by a factor of a few, providing a combined reduction in tcc by an order of magnitude. These are described in the three following subsections.
3.2.1. Rotation of clumps in simulations
We assume that the FFB galaxies and the clouds that fragment from them at cosmic dawn are qualitatively similar to the star-forming disk galaxies that are well studied, simulated and observed, at somewhat lower redshifts near cosmic noon (Dekel et al. 2009, 2022, 2023b; Genzel et al. 2011; Ceverino et al. 2012; Wuyts et al. 2012; Mandelker et al. 2014, 2017; Guo et al. 2015, 2018; Huertas-Company et al. 2020; Ginzburg et al. 2021). The rotational support of clumps that form by violent disk instability in thick gas-rich galactic disks at cosmic noon has been studied by Ceverino et al. (2012) using an analytic model, zoom-in cosmological simulations, and isolated-disk simulations. They measured the rotation support via the quantity 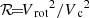 , where Vrot and Vc are the clump rotation and circular velocities respectively. Assuming Jeans equilibrium in the equatorial plane of the flattened clump, Vc2 = Vrot2 + 2σr2, where σr is the radial velocity dispersion, ℛ corresponds to the rotation-to-dispersion velocity ratio via
, where Vrot and Vc are the clump rotation and circular velocities respectively. Assuming Jeans equilibrium in the equatorial plane of the flattened clump, Vc2 = Vrot2 + 2σr2, where σr is the radial velocity dispersion, ℛ corresponds to the rotation-to-dispersion velocity ratio via 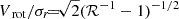 . The associated axial ratio assuming hydrostatic equilibrium perpendicular to the major plane of rotation is Rdisc/Hdisc ≃ Vrot/σr.
. The associated axial ratio assuming hydrostatic equilibrium perpendicular to the major plane of rotation is Rdisc/Hdisc ≃ Vrot/σr.
The analytic model of Ceverino et al. (2012), based on Toomre disk instability and conservation of angular momentum during clump formation, predicts ℛ ≃ 0.2 c, where c is the clump-radius contraction factor with respect to the protoclump patch, assumed to be at the disk mean density. At Jeans equilibrium this corresponds to 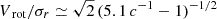 . We note that a contraction of c ≃ 5 brings the clump to full rotation support.
. We note that a contraction of c ≃ 5 brings the clump to full rotation support.
The distribution of ℛ over the clumps in pre-VELA zoom-in cosmological simulations as measured in Ceverino et al. (2012) is shown in Fig. 3. The median rotation support is ℛ = 0.79. Jeans equilibrium implies a median of Vrot/σr = 2.66 for these clumps. The most massive clumps tend to show a higher level of rotation support, with ℛ ≥ 0.75 spread about unity. Jeans equilibrium is found to be valid to a good accuracy for each clump, and ℛ is indeed spread about ℛ = 0.2c as predicted by the toy model, with c = 2 − 8. The values that exceed unity in Fig. 3 are indicative of the error that should be assigned to the ℛ values. They may result from clumps that deviate from equilibrium during formation or disruption, deviations from spherical symmetry, tidal effects from perturbations in the background disk, and so on.
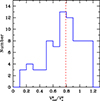 |
Fig. 3. Distribution of rotation support, |
We note in passing that today’s Galactic globular clusters, as observed by Gaia, are hardly rotating, with ℛ values in the range 0.003 − 0.14 for the 15/62 clusters for which any rotation has been detected (Sollima et al. 2019, Table 2). This distinguishes the high-redshift clusters from the local ones, if the former originated from rotating galactic disks according to the disk version of the FFB scenario.
3.2.2. Gravo-gyro instability
A rotating cluster would develop core collapse more efficiently due to a combined ‘gravo-thermo-gyro’ instability. The more familiar gravo-thermal instability (Lynden-Bell & Wood 1968) can be understood as a result of the negative specific heat of a self-gravitating system, represented by the virial theorem. When a kinematically hot core is embedded in a colder envelope, the energy transferred out of the core causes the core to contract and therefore heat up toward virial equilibrium, thus generating a runaway process. In analogy, the gravo-gyro instability (Hachisu 1979, 1982) can be interpreted as being due to the negative ‘specific moment of inertia’. When a rotating core is embedded in a slower rotating ring, AM is transferred out of the core. This causes the core to contract and its moment of inertia to decrease. In response, the core rotation speeds up (the ‘ballerina’ effect), generating a runaway process. The two instabilities help each other, as each generates contraction.
Following the early simulations by Ernst et al. (2007) and Kim et al. (2008), Hong et al. (2013) performed N-body simulations of a cluster, with a simplified IMF consisting of two populations of individual stellar masses m2 ≥ m1 and total masses M1 > M2, and they tested a range of dimensionless angular velocities ω0, as defined in and after their Eq. (1) for a King model (King 1962) following Lupton & Gunn (1987). For m2/m1 = 2 and M1/M2 = 5 (case M2A), comparing ω0 = 0 and 1.5, they find tcc/trlx = 6.8 and 2.8, namely a speed up by a factor of 2.4 because of the rotation. For m2/m1 = 20 (M2D) and no rotation they obtained tcc/trlx ∼ 0.42, namely a speed up by a factor 10 or more due to the more top-heavy IMF. This implies a crude dependence on the IMF of tcc ∝ (m1/m2). However, they found that with the high mass ratio the relative effect of rotation becomes weaker.
Kamlah et al. (2022) performed N-body simulations of a cluster, with a Kroupa (2001) IMF, including binaries and other complications, and tested a varying level of rotation ω0 = 0.0 − 1.8. The cluster mass is Mc = 1.1 × 105 M⊙, obeying a King model profile (King 1962), with parameters W0 = 6.0, rhalf = 1.85 pc, and rtidal = 65.59 pc. For ω0 = 1.8 they find tcc ∼ 3 Myr. Only a minor core collapse is seen for ω0 = 0.6, at tcc ∼ 30 Myr, with no clear evidence for core collapse in the non-rotating case. This is based on Figs. 1 and 2 of Kamlah et al. (2022) for the core radius, and Figs. 3, 4, and 6 for the flattening. This corresponds to a speed up by a factor of ∼10 due to rotation.
3.2.3. Flattening and dynamical friction
The simulations above assume little or moderate flattening for the initial rotating clusters, of axial ratio up to 0.4, comparable to the typical flattening of Toomre clumps in simulations of disks at cosmic noon (Ceverino et al. 2012). If the clusters are flatter, with h/r ∼ 0.2, say, similar to the parent galaxy, this would speed up the core-collapse via the shorter timescale for two-body relaxation and dynamical friction of massive stars. Based on our estimate below for the dynamical friction in a hot disk, Eq. (19), the effect of flattening could be tdf ∝ (h/r)2, namely an order of magnitude.
Combining the effects of rotation and flattening, we crudely assume in our feasibility study a speed up factor of 10 compared to the non-rotating core collapse time of Eq. (3). One should be cautioned that this is a tentative crude estimate, to be explored further by future, more detailed simulations.
3.3. Core collapse in FFB clusters
Figure 4 shows the threshold in the clump radius-mass plane for core collapse in 3 Myr in a rotating cluster, to be compared to Fig. 2 for a non-rotating cluster. The curves, shown for two different IMFs, are computed using the segregation time in Eq. (3), the one used in the right panel of Fig. 2, but here divided by 10 due to clump rotation and flattening.
 |
Fig. 4. Black hole growth in rotating FFB clusters with a broad IMF. Same as Fig. 2, right panel, based on Eq. (3) (Rizzuto et al. 2021, Eq. (4)), but with tcc reduced by a factor of 10 due to rotation (gravo-gyro instability; Hachisu 1979, 1982; Hong et al. 2013; Kamlah et al. 2022) and flattening. The FFB clouds that form by disk instability at the characteristic Toomre mass of ∼107 M⊙ (Dekel et al. 2023a), lie above the curve (magenta) that marks core-collapse in 3 Myr. However, if sub-Toomre clouds form by fragmentation with the same Σ, they should lie along the red line, such that core collapse will occur in 3 Myr for Mc ≤ 106 M⊙. The corresponding black-hole mass at the end of the FFB phase, Eq. (5), is Mbh ≤ 104 M⊙ (top axis). |
The maximum clump mass in a disk is assumed to be the characteristic Toomre mass as estimated in Dekel et al. (2009). In the FFB scenario, it is derived from the maximum gas mass in the disk during each FFB generation of ∼109 M⊙ to be (Dekel et al. 2023a, Eq. (58))
where λ = 0.025 λ0.025 is the inverse contraction factor from halo to disk (comparable to the halo spin parameter) and Mv = 1010.8 M⊙ Mv, 10.8 is the galactic halo virial mass at 1 + z = 10 (1 + z)10. Below this mass, we assume a distribution of clump masses following a power-law mass function
with α ∼ 1.8, as seen in simulations at cosmic noon (Mandelker et al. 2014, 2017). Such a mass function with α ≃ 2 is a generic result in a supersonic turbulent medium (Hopkins et al. 2013; Trujillo-Gomez et al. 2019; Gronke et al. 2022). The fraction of mass in clumps less massive than Mc is f(< Mc) = (Mc/MT)2 − α.
Assuming that the clumps of all masses are at the critical surface density for FFB, Σ = 3 × 103 M⊙ pc−2 (Dekel et al. 2023a; Menon et al. 2023), one can see in Fig. 4 that the most massive clumps of ∼107 M⊙ are above the threshold line, namely their core collapse takes longer than than 3 Myr. However, rotating clumps of ∼106 M⊙ and less should core-collapse in less than 3 Myr, namely during their FFB phase. Given the assumed clump mass function, 63% of the mass is in clumps below 106 M⊙, and 23% is in clumps between 105 and 106 M⊙. Based on Eq. (5), the BHs in FFB clusters of ∼106 M⊙ should be ∼104 M⊙, which we adopt as our fiducial values. Recall that certain subsequent growth is expected for BHs below this mass due to stellar capture, following Eq. (7), so the seed mass of ∼104 M⊙ should be considered a conservative estimate. We thus consider for the stages of evolution following the FFB phase a compact disk galaxy consisting of thousands of star clusters, with a characteristic mass ∼106 M⊙, each containing a central intermediate-mass BH seed of ∼104 M⊙.
4. Migration of black holes by dynamical friction
The BH seeds, that have been produced in the FFB clusters at cosmic dawn as described above, are subject to dynamical friction by the compact galactic stellar system and the dark-matter halo, which makes them migrate to the galactic center where they can coalesce into a SMBH. The question one wishes to verify is whether the SMBHs can grow this way by z ∼ 4 − 7 to ∼107 ± 1 M⊙ keeping a high fbh of ∼0.01, as observed. This requires rather efficient inward migration such that most of the seed BHs reach the SMBH by that time, namely in less than a Gigayear. We address this DF-driven inward migration here.
4.1. Disruption of clusters into a smooth medium
What is the origin of the particles that exert most of the dynamical friction on the BHs? The compact configuration of thousands of FFB star clusters is expected to turn rather quickly into a smooth galactic stellar system. This is unavoidable due to efficient tidal disruption by the mutual unbound cluster encounters, where clusters of internal velocities of ∼10 km s−1 orbit with higher relative velocities of ∼50 km s−1 in a compact thick disk configuration.
We study the evolution of such a system via an N-body simulation using the GADGET-4 code (Springel et al. 2021). The initial configuration of this idealized experiment consists of 2000 star clusters of 106 M⊙ each, randomly distributed in a galactic thick disk following an exponential surface-density profile. To match a typical FFB galaxy at 1 + z = 10 with an integrated SFE ϵ = 0.2 (Dekel et al. 2023a; Li et al. 2024b), the total stellar mass is Md = 2 × 109 M⊙ and the disk half-mass radius is Re = 470 pc1. The density profile perpendicular to the disk is exponential with a scale height of 60 pc above and below the plane. The disk is embedded in an analytic spherical dark-matter halo of virial mass Mv = 1010.8 M⊙ and virial radius Rv = 12.3 kpc, as predicted for typical FFB galaxies at 1 + z = 10. The halo density profile is NFW (Navarro et al. 1997) with a concentration parameter C = 10. The equilibrium initial conditions for the N-body disk are generated using the AGAMA code (Vasiliev 2019), where the clusters are tentatively represented by 2000 point particles. The cluster initial velocities are drawn from a quasi-isothermal distribution. The clusters are assigned circular velocities that grow from Vc ∼ 50 km s−1 at r = 0.1 kpc to Vc ∼ 185 km s−1 at r = 1 kpc and beyond. The three components of the velocity dispersion decline from σr ∼ σϕ ∼ 45 km s−1 and σz ∼ 65 km s−1 at r = 0.1 kpc to σx ∼ 15 − 20 km s−1 at r = 1 kpc and beyond. In a test run with the clusters represented by point particles, the density profiles remained stable for at least a Gyr, and so did the profiles of mean velocities and σz, while the profiles of σr and σϕ increase after about 0.5 Gyr to the level of 30 km s−1 beyond r ∼ 0.5 kpc.
Each star cluster of 106 M⊙ is assigned a half-mass radius of 7 pc, as predicted for the typical clusters in FFB galaxies (Dekel et al. 2023a), and is modeled as a Plummer sphere in equilibrium (Plummer 1911) with 10 000 particles. The Plummer-equivalent gravitational softening in the simulation is 0.7 pc. This softening was selected based on an equilibrium test, in which a single cluster of 104 particles was found to be stable over 200 Myr with a softening of order 10% of the cluster half-mass radius.
The simulation of 2000 clusters with 104 particles in each is run for 200 Myr, where the disk dynamical time, td = r/Vc, is 2.96 Myr at Re and 4.92 Myr at 2 Re.
Figure 5 shows a face-on projection of a subsample of the stellar particles at three different times in the simulation. One can see that the initial distribution of clusters gradually evolves inside-out into a smooth stellar disk, capable of exerting dynamical friction on the BHs that formed at the center of each cluster. By t = 50 Myr, the inner galaxy seems to contain a significant smooth component. By t = 200 Myr, the whole disk seems to be dominated by the smooth component.
 |
Fig. 5. N-body simulation of post-FFB cluster disruption and the buildup of a smooth stellar disk component capable of exerting dynamical friction on the BHs of each cluster. Shown is the projected stellar distribution in one quadrant of the galactic plane, in a slice of thickness ±50 pc, at different times. One thousand star particles are selected at random from each cluster. The colors represent radial distance at t = 0. The clusters survive mostly intact for a few tens of Myr, namely several cluster free-fall times, allowing FFB and core collapse to seed BHs in them. A significant smooth component is building inside-out to become dominant by ∼100 Myr, after a few galactic orbital times. |
Figure 6 illustrates the inside-out transition of the FFB galactic disk from an assembly of thousands of compact star clusters with central BHs into a smooth thick stellar disk capable of exerting dynamical friction on the BHs that formed within the clusters and are left naked after the cluster disruption. The fluctuative nature of the density is measured here by the standard deviation of the density fluctuation in the disk plane near radius r at time t. The density is measured in pixels of side 30 pc, comparable to the original cluster size, in order to pick up the signal from the clusters while they are intact.
 |
Fig. 6. Buildup of the smooth stellar disk component. The presence of clusters is measured by the standard deviation of the density fluctuation σδ in the disk plane near radius r at time t. The density is measured in pixels of side 30 pc, comparable to the original cluster size. The smooth component becomes significant, with σδ < 1, after ∼10 Myr, a few FFB cluster free-fall times, and before ∼100 Myr, several galactic orbital times. |
We first learn that most clusters survive intact for at least ∼10 Myr, namely for a few cluster dynamical times and a typical FFB single generation period, thus allowing for FFB within each cluster and the core collapse to a seed BH. As long as the clusters remain intact, they are subject to dynamical friction. The dynamical-friction timescale for a cluster of 106 M⊙ due to the dark-matter halo is estimated to be ∼10 Myr at r = 30 pc and ∼100 Myr at r = 70 pc. This indicates that a fraction of the clusters that originated from the central regions of the disk would migrate to the center before they are disrupted.
Second, we see that the rms fluctuation becomes smaller than unity after about three orbital times at the half-mass radius, and smaller than 0.5 over most of the disk mass after about ten orbital times. This indicates the presence of a significant smooth stellar component capable of exerting dynamical friction on the BHs soon after the FFB phase of the galaxy. For a typical FFB phase that began at zffb ∼ 9 (t ∼ 540 Myr) and lasted for ∼100 Myr, we thus expect the smooth component to be dominant for at least ∼500 Myr prior to z ∼ 5 (t ∼ 1150 Myr). We find below that the dynamical friction exerted on the BHs by this stellar disk is stronger than the dynamical friction exerted by the dark-matter halo, and evaluate the corresponding timescale for migration to the galactic center. The dynamical friction by the halo is not included in the above simulation.
We comment that our estimate of the timescale for the formation of a smooth disk is likely an overestimate. This is because the clusters, as they undergo core collapse associated with mass segregation, are also expected to undergo significant evaporation due to two-body effects within the clusters. This evaporation is suppressed in our simulations, as we tuned the softening length such that each cluster is stable when simulated in isolation.
4.2. Dynamical friction in a 3D medium
While dynamical friction is understood as a complex non-local process involving resonances (Tremaine & Weinberg 1984; Kaur & Sridhar 2018; Banik & van den Bosch 2021), a useful qualitative approximation can be obtained via the classical more local Chandrasekhar (1943) formalism, which sums up the two-body interactions between the moving massive object and the much less massive particles in the 3D medium. Consider a seed BH of mass m on a circular orbit with velocity V(r) at a radius r in a disk within an FFB galaxy (disk and halo) whose properties were determined at zffb (Dekel et al. 2023a; Li et al. 2024b). The DF acceleration by a spherical mass distribution of low-mass particles with a density profile ρ(r) and an isotropic Maxwellian distribution of velocities is approximated by
where
and where in the Coulomb logarithm
is derived by integrating over the distribution of orbit impact parameters. The estimate of M(r)/m arises from assuming for the maximum and minimum impact parameters bmax ∼ r and bmin ∼ Gm/V2, and using V2 = GM(r)/r. The DF acceleration then becomes
where F ≡ ℬlnΛ.
The timescale for migration into the center can be obtained by integrating the angular-momentum loss due to the torque dL/dt = τ = −m r adf. It can be approximated, as demonstrated by following the orbit from r to the center in an isothermal sphere (Binney & Tremaine 2008, Eq. (8.13)), by
Here M(r) is the total mass within r, and the circular velocity is approximated by V2 = GM(r)/r even if there is a contribution of a disk to the mass and to the circular velocity (this can be made more accurate). The last term is the dynamical crossing time of the system (as V/r = td−1 and (4πGρ)−1 = td2).
4.3. Dynamical friction in a disk
An analogous derivation of dynamical friction in a disk is apparently less straightforward and, quite surprisingly, there is no accepted textbook approximation analogous to the Chandrasekhar formula, neither based on analytic integration nor using simulations (e.g., Quinn & Goodman 1986; Donner & Sundelius 1993; Bekki 2009). We appeal here to our own crude analytic estimates, and test their qualitative validity with simple N-body simulations.
4.3.1. Analytic estimates of dynamical friction
Consider an object of mass m moving in a circular orbit at radius r within a disk that consists of much less massive particles, with a surface density profile Σ(r) and half-thickness h(r). The circular velocity Vc(r), and the associated angular-velocity Ω(r), are determined by the mass distribution in the disk and possibly an additional component, such as a bulge or a DM halo, whose direct contribution to the dynamical friction is neglected. We crudely approximate Vc2 = G M(r)/r, where M(r) is the total mass within a sphere of radius r, and tentatively assume for simplicity a flat rotation curve Vc(r) = const. We use the standard result that the disk is self-regulated to comparable kinematic and spatial axial ratios, V/σ = r/h, where σ is the radial velocity dispersion. This can be derived from hydrostatic equilibrium in the vertical direction assuming an isotropic velocity dispersion.
Building upon Eqs. (11) and (14), we adopt the Chandrasekhar expression for the magnitude of the DF acceleration,
where Vrel is now the relevant relative velocity between the object and the background particles exerting the force, and Fd is a proper numerical coefficient that results from the integration over the impact parameters and replaces the ℬ lnΛ factor of Eq. (11).
In the case of a kinematically hot, thick disk, or when m ≪ Md, the relative velocity is typically
A similar expression is obtained alternatively from the differential rotation as measured in the frame that is rotating with the object. We realize that the DF is dominated by impact parameters of order b ∼ h. This can be understood as follows. On the one hand, the gravitational force from each particle scales with b−2. Furthermore, the contribution of differential rotation to DF also scales with b−2 because the relative velocity is Vrel ∝ b to first order in b/r (or at any b for a flat rotation curve). On the other hand, the number of particles contributing to the DF increases as b2 when b < h due to the 3D nature of the distribution within the disk, while it only increases as b for b > h due to the 2D nature of the distribution on scales larger than the disk thickness. The key quantity Vrel in Eq. (17) is the differential rotation between radii r ± h and r once h ≪ r or when the rotation curve is flat. The relative velocity in Eq. (17) introduces an enhancement factor of (r/h)2 in adf.
However, due to the differential rotation, the rings outside and inside the object instantaneous radius r exert dynamical friction of opposite signs, where particles in the outer (inner) ring move with an angular velocity smaller (larger) than that of the object, thus exerting deceleration (acceleration). In a disk of uniform density these contributions would have balanced each other such that the net dynamical friction vanishes. However, for a declining density profile, if we write to first order in h/r
the second term makes a non-vanishing contribution to the dynamical friction. Substituting Eqs. (17) and (18) in Eq. (16), summing over the outer and inner rings, we obtain for the net DF deceleration in a hot disk
We note that for an exponential disk with an exponential scale radius r1 one has Σ′(r) r = − Σ r/r1, which is on the order of the surface density Σ in the main body of the disk.
The factor Fd is rather uncertain. The range of impact parameters can be assumed to be bounded from below by the Hill radius, where the outward tidal force is balanced by the object’s self gravity,
where γ is of order unity. It is γ = 3 if M(r) represents a point mass but it is smaller for a gradually declining density profile and it can vanish for a flat core (Dekel et al. 2003). For a very low-mass object, m ≪ M(r), one has RH ≪ r and RH < h. For example, with m ∼ 10−5M(r) and h/r ∼ 0.2, one has h/RH ∼ 10. Assuming bmax ∼ h, this range would correspond to lnΛ ∼ 2.3, and therefore to Fd of order unity, but its actual value has to be calibrated by simulations.
In the alternative case of a kinematically cold disk, or for m that is not extremely smaller than M(r), one has h < RH. In this case the effective impact parameter is b ∼ RH rather than b ∼ h. Replacing Eq. (17) with Vrel ≃ VcRH/r for the contribution of differential rotation to Vrel, and replacing h with RH in Eq. (18), we obtain by inserting in Eq. (16) that the net DF in a cold disk is
The numerical coefficient Fd here can be different from the coefficient in the hot-disk case, and it should be calibrated using simulations.
For a razor-thin disk, Valtonen et al. (1990) analyzed the dynamical friction in a Mestel disk, Σ ∝ r−1 with a flat rotation curve, and obtained (their Eq. (5))
This is similar to the analytic result by Quinn & Goodman (1986) in their Eq. (III.20), and to their simulations, but with a coefficient larger by a factor of a few due to a different analysis of the impact parameters and the inclusion of self gravity in the simulations. Valtonen et al. (1990) found Eq. (22) to be in general agreement with their 2D N-body simulations, although there is certain enhancement in the simulations by self-gravity, namely by resonances. Using Eq. (22) to calibrate our Eq. (21), for m = 0.04M(r) corresponding to the m = 0.04Md simulated by Valtonen et al. (1990), would give Fd r/h ∼ 1 near these values of m and at large radii. Interestingly, Valtonen et al. (1990) find (in their Fig. 2a) that with a self-regulated velocity dispersion at the level of Toomre Q = 1.4, the dynamical friction is not very different than in the razor-thin disk case, being weaker by only ∼30%. This is consistent with our finding that Eqs. (19) and (21) provide estimates in the same ball park for hot and cold disks and relatively large m.
4.3.2. Testing dynamical friction with simulations
In order to verify the order-of-magnitude validity of the above analytic estimates of the dynamical-friction timescale in a disk, we perform our own simplified N-body simulations using the GADGET-4 code (Springel et al. 2021). We simulate the orbital decay of massive point particles in a razor-thin, cold, truncated Mestel (1963) disk, with a surface density profile
where Md is the total disk mass and R0 is the disk truncation radius. The truncated Mestel disk has a flat circular velocity profile Vc, disk2 = (π/2) G Md/R0. The disk consists of 106 particles on circular orbits, assuming a Plummer-equivalent gravitational softening of 0.001R0. To help long-term stability, we add an inert isothermal-sphere halo with a circular velocity 3 Vc, disk, such that the total circular velocity of the system is Vc ≃ 3.16Vc, disk, but this halo does not exert additional dynamical friction.
We first verify the stability of the simulated disk for several orbital times, when it maintains its density profile while developing a modest velocity dispersion in the radial and tangential directions at the level of 0.1Vc. We then simulate the orbital decay of massive point-like objects of two different masses, m = 10−4Md and m = 10−3Md, with the same softening as that of the disk particles, starting on a circular orbit at radius ri. Figure 7 shows the radial migration of these massive particles, starting at either ri = 0.07R0 or 0.1R0. The migration timescale in these simulations is found to be shorter by a factor ∼3 than the time derived by the crude approximation tdf = 0.5Vc/adf from Eq. (22). The simulated DF timescale is comparable to the time derived from Eq. (21) with Fd r/h ≃ 6. The analytic curves that are shown in comparison to the simulations in Fig. 7 are obtained by solving for a particle orbit under the smooth force due to the enclosed mass at a given radius and the expression for the force of dynamical friction. For a razor-thin disk, the acceleration in Eq. (22) is multiplied by a numerical constant Fd, which is tuned for a crude simultaneous match to the four simulation results. For a cold disk, the value of Fdr/h is tuned in Eq. (21). A reasonable match to all four cases is obtained for a factor Fd = 5 multiplying Eq. (22), and for Fdr/h = 10 in Eq. (21), the curves shown in the figure. The fact that these factors are somewhat different from the fits to tdf quoted above partly reflects the inaccuracy of the approximation tdf ∼ 0.5Vc/adf.
 |
Fig. 7. Testing the inward migration by dynamical friction in a disk. The solid curves refer to N-body simulations of a BH of mass m starting in a circular orbit at ri within a thin live Mestel disk with an isothermal halo as an external potential. The left and right panels refer to ri = 0.07R0 and 0.1R0. Shown for comparison are analytic estimates based on Eq. (21) (dotted) and Eq. (22) (dashed), crudely normalized for best overall fit in the four cases. We learn from this comparison that the analytic approximations are realistic conservative estimates. |
This simple test with simulations indicates that the analytic estimates of Eqs. (19) and (21), with tdf ∼ 0.5Vc/adf, can be used for our purpose of a crude, conservative estimate of the dynamical-friction timescale in a cold disk.
4.4. An FFB galaxy exerting dynamical friction
According to the FFB model (Dekel et al. 2023a), most FFB galaxies occur at redshifts zffb ≥ 8 in halos near and above a threshold mass of
where Mv ≡ 1010.8 M⊙ Mv, 10.8 and 1 + z ≡ 10 (1 + z)10. The corresponding halo virial radius is
We assume that the BHs are initially distributed within an FFB exponential stellar disk, which turns out to dominate the dynamical friction. The disk mass is
where the star-formation efficiency ϵ may range from 0.2 to unity. The disk half-mass radius is (Li et al. 2024b)
The 1σ scatter in size derives from the scatter in the spin parameter, σlnλ ≃ 0.5, namely a multiplicative factor of 1.6. The disk profile is assumed to be exponential,
with the exponential radius r1 = Re/1.68. The corresponding disk mass profile is
The gradient, if needed, is
Again, we approximate Vd2 = GMd(r)/r.
While the contribution of the dark-matter halo to the dynamical friction turns out to be negligible compared to that of the disk, as seen in the left panel of Fig. 8, we include it for completeness. We assume an NFW dark-matter halo profile
 |
Fig. 8. Supermassive BH mass (left) and BH-to-stellar mass ratio (right) as a function of redshift for zffb = 9 (blue) and 12 (magenta), with m = 104 M⊙. This is either in a hot disk (Eq. (19), solid) or in a cold disk (Eq. (21), long-dashed). The FFB-threshold halo properties as a function of zffb are from Eqs. (24) and (25) (Dekel et al. 2023a). The SFE is ϵ = 0.2. The BHs are assumed to be on circular orbits responding to DF from the stellar disk (V/σ = 5) plus an NFW DM halo (whose contribution is negligible, short dashed). The BHs are assumed to start in an exponential disk whose radius is estimated in Eq. (27) (Li et al. 2024b). The galaxy stellar mass, assumed to be constant in time, is marked (dotted). The 1σ scatter due to the scatter in disk size in Eq. (27) is ±0.2 dex. Eddington growth is marked for comparison (thin dashed green) The observational estimates are shown for comparison. The data are from Maiolino et al. (2024b) (circles), Harikane et al. (2023) and Übler et al. (2023) (squares). The selection-bias-corrected mean and standard deviation by (Pacucci et al. 2023) based on the data in red symbols are marked by the red lines. The values of fbh at z = 4 − 7 are > 3σ above the standard z = 0 low-z ratio by Reines & Volonteri (2015) (indicated by dashed green lines). The average SMBH masses and fbh ratios as deduced from the observations at z ∼ 4 − 7 are reproduced by the 104 M⊙ seeds of the FFB scenario. |
where x = r/rs and the concentration parameter is C = Rv/rs. We adopt C = 4 at high z (Zhao et al. 2009, Fig. 20). The NFW mass profile is
With the free parameters Mv and C, we have rs = Rv/C and ρs = Mv/[4πrs3A(C)]. The halo contribution in quadrature to the circular velocity is Vh2 = GMh(r)/r.
We very crudely assume here that the galaxy does not grow from the FFB phase to the epoch when the SMBH is detected, an assumption that may cause an overestimate in fbh. The average halo growth between z = 9 and z = 7 is expected to be by a factor of exp[0.8 * (9 − 7)] ∼ 5 (Dekel et al. 2013), namely by less than an order of magnitude. This can serve as a conservative upper limit for the potential growth of stellar mass. The large stellar mass produced already in the FFB phase, and the evidence from JWST for rapid quenching soon after cosmic dawn (de Graaff et al. 2025; Weibel et al. 2024; Antwi-Danso 2024), support the simplified assumption of a more limited growth of stellar mass. This assumption is to be relaxed in future cosmological simulations.
4.5. Inspiraling and mergers into a supermassive black hole
We assume that the seed BHs of mass m at zffb are distributed in the FFB disk of mass Md, with values of fbh that are determined by the core collapse in the FFB clusters. The total BH mass is thus fbh Md.
At any given radius r, we compute the density, mass and circular velocity profile of the disk and the halo and their sums. The circular velocities are approximated assuming spherical symmetry. The DF acceleration at r is computed from the sum of the contributions of the two components, and the DF time tdf(r) is derived from it. The SMBH mass at a Universal time t = tffb + tdf(r) is assumed to be the sum of the BH seed masses that were initially in the disk at radii smaller than r (ignoring any mass loss by recoils, to be discussed in Sect. 5).
At a Universal time t, we approximate the redshift by
where t1 = 17.5 Gyr (Dekel et al. 2013). This is used at zffb and at any other z.
The predicted SMBH mass at redshift z and the corresponding BH-to-stellar mass ratio are shown in Figs. 8 and 9 as a function of z, in comparison to the observational estimates at z = 4 − 7. This is under the tentative assumption that the BH seeds that reach the central region of the galaxy by DF-driven migration indeed merge efficiently into a central SMBH (to be reconsidered in the following section). In Fig. 8 the seed mass is assumed to be m = 104 M⊙ based on Fig. 4, with fbh ∼ 0.01 based on Eq. (5). Shown are the predictions for FFB at zffb = 9 and 12. Figure 9 illustrates the scatter in the SMBH growth via different cases of BH seed mass and galaxy mass above the FFB threshold, for zffb = 10. The dynamical friction in the disk is estimated either by Eq. (19) (hot disk, solid curves) or by Eq. (21) (cold disk, dashed curves). The FFB galaxy stellar mass, which is very crudely assumed here to remain constant since zffb, is shown for comparison (dotted line) in the panels showing the SMBH mass. The FFB-threshold halo properties that are adopted in the calculation as a function of zffb are from Eqs. (24) and (25) (Dekel et al. 2023a). In the fiducial case, the assumed integrated SFE is ϵ = 0.2, based on the tentative best fits reported in Li et al. (2024b) between the FFB predictions and a variety of JWST observations of galaxies at cosmic dawn. This value of average SFE indeed reflects the predicted duty cycle of the star-formation history during the ∼100 Myr FFB phase (Li et al. 2024b, Fig. 9). The BHs are assumed to be on circular orbits responding predominantly to the DF from the stellar disk (with V/σ = 5 in Eq. (19) or Eq. (21)). The additional contribution from an NFW halo turns out to be negligible. The BHs are assumed to start in an exponential disk whose radius is estimated in Eq. (27) (Li et al. 2024b). An additional ±1σ scatter due to scatter in the disk size in Eq. (27) corresponds to ±0.2 dex.
 |
Fig. 9. Scatter in SMBH mass. Same as Fig. 8 but for zffb = 10 and for three caes: Middle, blue: the fiducial case, with ϵ = 0.2, halo mass at the FFB threshold, and seed BHs of m = 104 M⊙, is recovering the average BH mass at z = 4 − 7. Top, magenta: with ϵ = 1 and halo mass 3x the FFB threshold, the model reproduces the most massive BHs at z = 4 − 7. Bottom, green: with seed BHs of m = 103 M⊙, the BH growth in a hot disk is not sufficiently fast. |
We learn from Fig. 8 that if the DF in the disk is acting according to the estimate for a hot disk, Eq. (19), the fiducial model with m ∼ 104 M⊙ reproduces the median z = 4 − 7 observations both in terms of BH masses and the high fbh ratios. We learn further from Fig. 9 that in the case of a cold disk, Eq. (21), even more modest seeds of m ∼ 103 M⊙ could make it to the SMBH in time, starting from FFB at zffb ∼ 10.
In terms of the typical timescale for the DF-driven inspiral of the BHs to the galaxy center, for the case shown in Fig. 8 with zffb = 9 and m = 104 M⊙, the time it takes for half the total BH mass to reach the center is 0.1 Gyr (z = 7.9) and 0.9 Gyr (z = 4) for the cold disk and the hot disk, respectively. The average between a cold and a hot disk would be ∼0.5 Gyr (z ∼ 5.5) for accumulating half the total BH mass at the center.
The most massive BHs in the z = 4 − 7 sample, of ∼108 M⊙, can be reproduced in post-FFB galaxies at the tail of the distribution of the model parameters, for example, if the halo mass is a few times the threshold mass for FFB, or if the SFE is at the high end toward unity, or if the optimal conditions for SMBH growth are pushed to their limit. These include a top-heavy IMF and strong rotational support that speed-up the core collapse to seed BHs in the FFB star-forming clumps, a cold galaxy disk configuration with a steeply declining surface density and angular-velocity profiles for rapid DF-driven inward migration, and a cold disk of BHs for spin-orbit alignments that minimize the suppression of BH growth by GW recoils (see the following section). In addition, as discussed below in Sect. 6, strong wet compaction events (e.g., due to galaxy major mergers) can boost the SMBH growth to its extreme efficiency. We also recall that the merger-driven scenario is only one of the mechanisms for SMBH growth; it is likely to be accompanied by central accretion-driven growth via an accretion disk, which can boost the BH mass and may possibly increase fbh to higher values.
The mass range of galaxies that host SMBHs is expected to be rather broad, as observed at z = 4 − 7. FFBs are expected in all galaxies above a threshold halo mass that decreases steeply with redshift, Eq. (24), based on Eqs. (62) and (67) and Fig. 6 of Dekel et al. (2023a). Therefore, a range of values for the epoch of FFB, zffb, is expected to lead to a wide range of stellar masses for galaxies that host over-massive SMBHs, ranging from below 108 M⊙ to above 1010 M⊙.
One should note that the dark-matter halos that cross the threshold mass for FFB, Eq. (24), represent high-sigma peaks (> 4σ) in the initial density fluctuations. By z ∼ 5 the post-FFB halos are expected to grow to halo masses of ∼1012 M⊙, with number densities in the ball park of ∼10−5 Mpc−3.
Over-massive BHs can be produced at higher redshifts, out to z ∼ 10 and beyond, as observed in a few cases (Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024a), in galaxies that underwent FFB at even higher redshifts. This is demonstrated in Fig. 8, which also shows the estimated BH mass and fbh for a galaxy that underwent FFB at zffb = 12. It shows that the high values as observed at z ∼ 10 can be obtained even for hot galactic disks, in galaxies of a stellar mass of ∼4 × 108 M⊙. FFB galaxies that formed at zffb = 15 would lead to over-massive BHs in galaxies of stellar mass as low as ∼108 M⊙.
A note of caution is that the DF-driven inward migration of the BHs may be suppressed by scattering against the irregular stellar distribution. This is indicated in zoom-in cosmological simulations of BHs in high-z dwarf galaxies, utilizing a subgrid model for capturing the unresolved dynamical friction acting on the BHs (Pfister et al. 2019). This emphasizes the need for the post-FFB galaxies to be rather cold disks in order to make the sinking into the central regions efficient. It adds to the requirement of cold disks in order to avoid BH ejections by post-merger recoils, to be discussed in Sect. 5. On the other hand, spiral arms that can form in a cold disk may weaken the DF-driven migration. Challenging, high-resolution simulations of the DF-driven cluster and BH migration in a realistic post-FFB disk galaxy are clearly needed in order to investigate the validity of DF-driven migration as well as the BH mergers and the effect of recoils.
5. Gravitational-wave recoil and the final parsec
Our prior calculations of SMBH growth in FFB galaxies (Sect. 4.5, Figs. 8 and 9) implicitly assume that every BH seed that makes it to the galactic center will merge with the central BH, culminating eventually in merger-driven SMBH production. This sequence of runaway seed BH mergers parallels the runaway stellar mergers that produced the seed BHs in the first place inside their birth clusters. However, there are, in principle, multiple steps along the way that could derail this “runaway of runaways” as the BHs approach the galaxy nucleus. One is the “final parsec problem” and the other is the post-merger recoils, to be examined next.
5.1. The final parsec problem
The “final parsec problem” (Begelman et al. 1980) is thought to suppress massive BH mergers in galactic nuclei. In brief, a circular-orbit BH binary can only merge due to gravitational wave emission in less than a Hubble time if it is already extremely tight, with a semi-major axis smaller than a milliparsec. However, dynamical friction ceases shrinking the binary orbit once it becomes “hard” with respect to the surrounding stellar population, typically on scales 1 − 10 pc. Therefore, if massive BH binaries are to merge in galactic nuclei, some additional hardening process must operate on sub-pc scales (Merritt & Milosavljević 2005).
The simplest of these processes is repeated strong three-body scatterings with stars in the galactic nucleus. Ejection of stars to infinity can in principle drain enough energy to shrink the BH binary down to milliparsec scales. While this process is relatively inefficient in spherical symmetry (Milosavljević & Merritt 2003), it is greatly accelerated in asymmetric potentials where stellar orbits fail to conserve angular momentum (Merritt & Poon 2004). Even a small degree of nuclear triaxiality (only a ∼5% deviation from axial symmetry) can efficiently solve the final parsec problem through stellar ejections (Vasiliev et al. 2015). We speculate that this triaxiality should arise naturally in the messy and dynamically young environments of FFB galaxies.
Furthermore, the BHs migrating to the center are likely to carry with them clumps of stars from the original FFB clusters. When such systems merge, the stars can help tighten the BH binary, either at the center, or while spiraling in.
In addition, the presence of significant amounts of nuclear gas may help solve the final parsec problem via circum-binary torques from active galactic nucleus accretion disks (Armitage & Natarajan 2002). This scenario is interesting insofar as accretion from gas disks will independently lead to SMBH growth (beyond what is provided from hierarchical BH mergers). We caution, though, that as a solution to the final parsec problem, gas torques can be self-limited by Toomre instability (Lodato et al. 2009), and in some circumstances can even lead to binary expansion Lai & Muñoz (2023). The process of wet compaction discussed in Sect. 6 is a natural way to bring in the necessary gas into the galaxy nucleus.
If none of the above scenarios efficiently harden the orbits of nuclear BH binaries, the secular and chaotic dynamics of BH triples may help. The large number of inspiraling BHs means that BH binaries will not live in isolation for long, and if they do not quickly merge due to gas torques or triaxiality-driven stellar scatterings, they will soon become part of a BH triple system. If the BH triple is hierarchical, the inner BH binary will often be driven to merge from Kozai-Lidov oscillations (Blaes et al. 2002), though in some orbital configurations this will not occur. Conversely, if the triple becomes non-hierarchical, then strong, chaotic scatterings will result, with three possible outcomes, each with order unity probability. First, a pair of BHs may merge promptly (Hoffman & Loeb 2007; Ryu et al. 2018; Bonetti et al. 2018). Second, one or more BHs may be ejected from the system. It is generally the lightest BH that is ejected, and this ejection may trigger the merger of the remaining pair (Bonetti et al. 2018). Third, the outcome of strong scattering may be to create a hierarchical triple that does not evolve significantly over a Hubble time. However, the nature of our FFB galactic system makes it unlikely that three-body ejections can derail runaway growth of the central object. Low ejection velocities mean that the ejected BH will usually return to the galactic center (Bonetti et al. 2018), and strongly preferential ejection of the lightest object means that a heavy central SMBH cannot be lost in this way. Likewise, “failed triples” (situations in which three-body dynamics does not solve the final parsec problem) will not be the end of the story as continued infall of new BH seeds means that eventually, fourth or fifth BHs will arrive to trigger chaotic orbital evolution and new strong scatterings.
Given the variety of ways in which our systems can solve the final parsec problem, one may argue that this is not likely to be the obstacle to SMBH growth by mergers. We therefore focus our attention on a potentially more serious bottleneck: GW recoil.
5.2. Recoil velocity
When two BHs merge, the merged BH suffers a recoil caused by the anisotropic emission of gravitational radiation. When the recoil velocity exceeds the escape velocity from the galaxy, it removes the BH from the central regions and suppresses the initial growth of the SMBH by mergers. The recoil velocity is robustly estimated using non-linear general relativistic calculations (Campanelli et al. 2007; Schnittman et al. 2008; Lousto et al. 2010; Gerosa & Kesden 2016). It is a strong function of the mass ratio q = m2/m1 ≤ 1 while it is independent of the absolute values of the masses. It also depends sensitively on the spins of the BHs, the angles between the spins and the merger orbit, and for misaligned cases on the phase of the orbit at the merger (considered to be a random variable).
Figure 10 shows the recoil velocity as a function of the mass ratio for certain cases of spins. A fitting formula for non-spinning BHs is provided by (Le Tiec et al. 2010)
 |
Fig. 10. Recoil velocity of the merged BH due to a merger between two BHs as a function of their mass ratio q = m2/m1. The cases shown are (i) non-spinning BHs (red), (ii) a strongly spinning BH a1 = 0.9 where the spin is aligned with the orbit (blue), (iii) strongly spinning BHs a1 = a2 = 0.9 (with respect to the maximum possible a1 = 1) with the spins aligned with the orbit (magenta), and (iv) a strongly spinning BH a1 = 0.9 with the spin inclined at 10° or at 30° with respect to orbit, spanning the full range of phases for the encounter (diagonal lines area and shaded area, respectively). Marked in comparison are the fiducial and maximum escape velocities from an FFB galactic disc of 171 and 700 km s−1 (black dashed, gray dashed). |
where η is the symmetric mass ratio, η = m1m2/(m1 + m2)22. This gives a maximum of Vrecoil = 175 km s−1 for η = 0.19, corresponding to a mass ratio q = 0.37. The peak is rather narrow, dropping to below 100 km s−1 at η = 0.24 − 0.25 (q > 0.67) and at η < 0.12 (q < 0.16). The dependence on q points to a potential bottleneck that may suppress the initial growth of the SMBH during the first few mergers, when the SMBH is still of a low mass such that the mass ratio tends to be rather large, q > 0.1. We learn that with no BH spins, or with highly aligned spins and orbit, this bottleneck can be overcome once the escape velocity is modest, of order 100 − 200 km s−1, as expected in typical FFB galaxies. However, we learn from the figure that this bottleneck can be more difficult to overcome for large spins and for misaligned spin and orbit unless the escape velocity is higher than expected for typical FFB galaxies.
5.3. Escape velocity
The recoil pushes the merged SMBH from the galaxy center to a maximum distance rhalt, which one may wish to estimate as a function of Vrecoil. Consider a mass profile M(r) and approximate the circular velocity as Vc2 = GM(r)/r and the inward acceleration as a = GM(r)/r2 such that a = Vc2/r. Assume that the inner rotation curve is rising with r while the magnitude of the inward acceleration is constant or declining with r. This is the case, for example, for a self-gravitating exponential disk inside its maximum velocity at 1.063 r1, or for an NFW DM halo inside its radius of maximum velocity. Given that at any r ≤ rhalt along the way a(r) ≥ a(rhalt), we can then write
where the r.h.s. is the halt radius for an initial velocity Vrecoil and a constant acceleration a(rhalt). Using a(rhalt) = Vc(rhalt)2/rhalt, we obtain
This implies that as long as 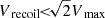 , one has Vc(rhalt) < Vmax, such that rhalt < rmax, where rmax is the radius where the rotation curve is at a maximum value Vmax, a characteristic radius for the galaxy. This limits the recoil of the central BH to inside rmax, where it can migrate back to the center on a timescale that is comparable to the migration timescale within the inner body of the disk as estimated in Sect. 4.3, provided that the recoil is in the disk plane. We therefore consider the effective escape velocity to be
, one has Vc(rhalt) < Vmax, such that rhalt < rmax, where rmax is the radius where the rotation curve is at a maximum value Vmax, a characteristic radius for the galaxy. This limits the recoil of the central BH to inside rmax, where it can migrate back to the center on a timescale that is comparable to the migration timescale within the inner body of the disk as estimated in Sect. 4.3, provided that the recoil is in the disk plane. We therefore consider the effective escape velocity to be 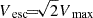 . A recoil with a higher velocity will prevent this BH from growing into a central supermassive BH.
. A recoil with a higher velocity will prevent this BH from growing into a central supermassive BH.
In an exponential disk rmax ≃ 1.8r1 with Vmax ≃ 1.063V1, where V1 is the rotation velocity at the exponential radius r1. For an exponential disk at the FFB threshold line 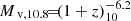 , using the disk properties from Eq. (27) to Eq. (29), we obtain
, using the disk properties from Eq. (27) to Eq. (29), we obtain
This implies 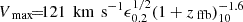 , and
, and
This escape velocity for a fiducial FFB disk at zffb ∼ 10 is rather similar to the maximum kick velocity for non-spinning merging BHs in Eq. (34). It implies that, in the absence of BH spin, or when the spins are aligned with the orbital angular momentum, the SMBH is not pushed to outside the central regions of the disk, and it can be pulled back by dynamical friction to the galaxy center within the migration timescale estimated in Sect. 4.3. However, as indicated in Fig. 10, spin-orbits misalignment introduces a non-trivial bottleneck which would require a higher escape velocity.
An additional bulge or DM halo would tend to increase Vmax and Vesc. In particular, the wet compaction events discussed in Sect. 6, which are common in massive galaxies at high redshifts, would significantly enhance the escape velocity, typically to 400 km s−1 and possibly up to 700 km s−1 (Lapiner et al. 2023). Based on Fig. 10, such escape velocities may be high enough to overcome the bottleneck introduced by GW recoil even for spinning BHs in relatively hot disks. This will be quantified below using Monte-Carlo simulations of sequential BH mergers.
5.4. The mass function of merging black holes
In order to simulate the growth of the SMBH by a sequence of binary mergers of seed BHs, one needs to know the effective mass function of the incoming BHs as they arrive at the galaxy center at a given time t. The initial mass function of the seed BHs is assumed to follow that of the FFB star clusters, Eq. (10), which we assume to be the same at all radii in the galaxy disk, namely
normalized such that ∫ϕ(m) dm = M, with M the total mass in BHs. At time t, the desired mass function of merging BHs at the galaxy center, ψ(m, t), is modulated by the number of BHs that started their inward migration at t = 0 in a radius within the ring (r, r + dr) and reach the center during a time interval (t, t + dt). The radius of origin of these BHs at t = 0, r(m, t), is to be derived from the expression for the dynamical-friction time at r. At t = 0, the number of BHs of mass in the range (m, m + dm) in the ring (r, r + dr) is
At t, the number of BHs in the same mass interval that arrive at the center during (t, dt) is
Here m and t are the independent variables, and the second equality represents a transformation of variables from t to r using the Jacobian ∂r/∂t at a given m. Extracting dN/(dm dr) at t = 0 from Eq. (40), and inserting it in Eq. (41), we finally obtain
The desired r(m, t) can be obtained, for example, using the DF acceleration adf, hot of Eq. (19), with t = tdf = 0.5Vc/adf. The radius r(m, t) is extracted by solving the equation
where 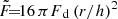 is a dimensionless constant and Σ′(r) = dΣ/dr.
is a dimensionless constant and Σ′(r) = dΣ/dr.
 |
Fig. 11. Negative slope β of the mass function of BH seeds as they merge with the central SMBH, ψ ∝ m−β. It is derived using Eq. (42) assuming an original BH mass function ϕ ∝ m−2 everywhere in the disk, a disk of BHs with a power-law surface density profile Σ ∝ r−γ, and a total circular velocity Vc ∝ rμ (which may include the additional contribution of a halo and a post-compaction central mass). At time t and mass m, these two power laws are relevant for the radial region from which BHs of mass m arrive to the center at time t, as derived for a hot disk using tdf = 0.5Vc/adf and adf from Eq. (19). Self-gravitating disks with the shown μ are marked by red circles. We read, for example, that for a flat rotation curve (μ = 0) and for the BHs that arrive from the disk range where Σ ∝ r−1 (a self-gravitating Mestel disk) the mass function at the center is ψ ∝ m−1.5. These values of β refer to the mass function used in the recoil simulations summarized in Fig. 13. |
 |
Fig. 13. Simulation results for the the GW recoil bottleneck. Shown is the threshold escape velocity Vesc that is required for SMBH growth in at least one third of the cases as a function of the slope β of the BH mass-function ψ ∝ m−β. The blue lower curves are for cold disks, with spin-orbit misalignments θ = 0 − 10°, while the red upper curves correspond to hot disks, with θ = 0 − 30°. The solid and dashed curves refer to cases where the mass of the initial primary BH m0 is either drawn from the seed BH mass function in (102 − 104 M⊙) or selected to be 104 M⊙, respectively. The fiducial escape velocity for an FFB disk at zffb = 9 is Vesc ≃ 170 km s−1 when ignoring compaction events, and it could rise to several hundred km s−1 after compaction (horizontal dotted lines). Naturally, the required escape velocity for BH growth is lower for a steeper BH mass function. For no BH spins, or fully aligned spin and orbit, there is always growth for Vesc ≥ 100 km s−1 (not shown). For a cold disk, The fiducial Vesc ∼ 200 km s−1 of FFB is sufficient for BH growth if β ≥ 1.5 (or β ≥ 1) for a random m0 (or m0 = 104 M⊙). The bottleneck becomes more severe for a hot disk, where a non-negligible growing fraction can be obtained either with a Vesc that has been boosted by compaction events to the level of a few hundred km s−1, or with the original FFB Vesc ∼ 200 km s−1 if m0 > 3 × 104 M⊙ (not shown). |
As an example, we consider a power-law surface density profile for the disk, Σ ∝ r−γ with 0 ≤ γ ≤ 2, and a power-law circular velocity profile Vc ∝ rμ with −0.5 ≤ μ ≤ 1. For a self-gravitating disk we expect μ = (1 − γ)/2, but we allow the circular velocity to include the additional contribution of a spherical halo and a post-compaction central mass. The solution of Eq. (43) is r ∝ (m t)1/(3μ + γ + 1), which gives in Eq. (42)
where β = α − (2 − γ)/(3μ + γ + 1). Figure 11 shows the negative slope β as a function of γ and μ, for an assumed α = 2 in Eq. (39). For a BH mass m at time t, one can interpret the power-law profiles with γ and μ as local approximations near r(m, t). After a certain time, when the massive BHs arriving at the center have originated from the main body of the disk, one may expect γ ∼ 1 or even steeper. For a self-gravitating disk, starting with α = 2, we obtain β = 1.2, 1.5, 2.0 for the cases (γ, μ) = (0, 0.5),(1, 0),(2, −0.5) respectively. We adopt as our fiducial case ψ ∝ m−1.5, as derived for a self-gravitating Mestel disk, (γ, μ) = (1, 0).
As another example, for a self-gravitating exponential disk with a scale radius r1, at early times when r ≪ r1, Eq. (43) gives r ∝ m2/3, which yields in Eq. (42) β = 0.67.
 |
Fig. 12. Growth of supermassive BH by mergers in four simulations of one example case, where the initial primary mass is drawn from the BH mass function of β = 1.13, the spin-orbit misalignment angle is randomly drawn from 0 − 10°, and Vesc = 200 km s−1. The sequence of mergers is represented along the x axis by the accumulated mass of the merging BHs from the initial primary mass to a total of 107 M⊙. Top left: the mass of the merged BH after each merger. Top right: the recoil velocity in comparison to the escape velocity. Bottom left: the mass ratio (when it is larger than unity, the primary and secondary exchange roles). Bottom right: the spin of the primary BH. When Vrecoil > Vesc the SMBH is ejected and a new primary is chosen. This is more likely to happen in the early mergers, when the mass ratio tends to be high. Three of the SMBHs manage to eventually grow while one fails (blue). Growth is practically guaranteed once the SMBH mass exceeds 105 M⊙, while the secondary merging BHs are limited to ≤104 M⊙ such that the mass ratio drops below 0.1. |
We assume as our crude fiducial slope for the seed BHs α = 2, only slightly steeper than the original α = 1.8 for the clusters from simulations. The effect of stellar capture within the clusters, based on Eq. (8), could in principle lead to a steeper slope at low masses and late times, but considering the disruption of clusters over time, we conservatively adopt only a modest steepening to α = 2.
5.5. Monte Carlo simulations of recoils
Using fitting formulae for the recoil velocity as a function of the given merger parameters, namely the mass ratio, the BH individual spins and the spin-orbit alignments (based on Gerosa & Kesden 2016; Gerosa et al. 2023), we ran Monte Carlo simulations of SMBHs as they grow by a sequence of binary mergers. We wish to evaluate the fraction of galaxies within which the SMBH would overcome the early recoil bottleneck as a function of (i) the escape velocity, (ii) the thickness of the disk of BH seeds, which determines the spin-orbit alignment and SMBH spin buildup, (iii) the choice of the initial primary central BH mass, and (iv) the mass function of BHs as they merge with the SMBH via the slope β of Sect. 5.4.
In each sequence, the potential SMBH starts from a given primary BH of mass m0. Its mass is either drawn at random from the mass function of seed BHs, or it is fixed at an assumed value, for example, m0 = 104 M⊙ or 105 M⊙. The latter scenario may be more realistic if a different high-z process, such as direct collapse of a mini-halo (Inayoshi et al. 2020), produced a single high mass BH seed that reached the galaxy center before the BHs produced in FFB clusters could arrive there.
The evolution of each galaxy, with a given escape velocity, is represented by a sequence of binary mergers, for which the mass of the secondary is drawn at random from the mass function in Eq. (44) with a given value of β. The simulation continues till the total accreted mass amounts to 107 M⊙, motivated by the SMBH masses obtained in Sect. 4 and detected at z = 4 − 7. The post-merger central BH mass, calculated using Barausse et al. (2012), becomes the new primary mass for the subsequent merger unless Vrecoil ≥ Vesc, in which case the merged remnant is ejected, and the sequence restarts with a new primary seed of mass m0. The post-merger central BH spin is assumed to be the sum of the spins of the two merging BHs and the angular momentum of the orbit with the appropriate numerical-relativity corrections (Hofmann et al. 2016). For this purpose we approximate the spins to be aligned with the galactic angular momentum as the misalignment angles are always small. The spin-orbit angles are drawn at random in the range 0 − θmax, with θmax = 0, 10° ,30°. These three choices represent pure alignment, a cold disk and a hot disk, respectively. We take all spin-orbit misalignments to be prograde, assuming that the orbit and the spins reflect the same original galactic disk angular momentum, and that the seed BHs are confined to the disk plane more than the stars due to dynamical friction in the vertical direction (Stewart & Ida 2000).
Figure 12 shows some details of four example Monte-Carlo simulations of mergers of seed BHs. Here θmax = 10° and the initial primary BH drawn at random from the same seed mass function (in this case with β = 1.13). One can see many repeated ejections of the SMBH, where the merged BH mass drops sharply to a new m0. These occur preferentially in the first few mergers of each sequence, where the BH mass ratios are high. Nevertheless, despite the high cumulated spins, three out of the four cases eventually reach the continuous growth phase in which mergers of increasingly diminished mass ratios yield lower and lower recoil velocities.
Figure 13 presents a summary of our Monte-Carlo simulation results for the recoil bottleneck. We show the threshold escape velocity, Vesc, that is required for SMBH growth (exceeding 106 M⊙) in at least one third of the simulated cases out of 1000 cases in each of our experiments, as a function of the slope β of the mass-function of the BHs as they reach the galaxy center. The fraction of growing SMBHs rises steeply from zero to unity as a function of Vesc near the critical value shown. The different curves refer to different levels of spin-orbit misalignments, resulting from the ‘cold’ and ‘hot’ disks specified above, and to two different choices of the primary central BH at the start of each sequence, both rather conservative choices. Recall that the fiducial escape velocity for an FFB exponential disk at zffb = 9 is Vesc ≃ 170 km s−1 when ignoring the effects of compaction events, and it could rise to several hundred km s−1 after compaction.
Not shown in the figure is that we find 100% SMBH growth for the cases of aligned spin-orbit or no spins, even for a random initial primary mass, for any escape velocity larger than 100 km s−1 and all choices of m0 and β in the ranges considered. This is despite possible failures during the first few mergers in certain cases. We also find 100% growth for more massive central primaries of m0 = 105 M⊙ in all the cases tested for β, θmax and Vesc > 100 km s−1.
We see in Fig. 13 that, in general, for a given Vesc, the growing fraction becomes larger for steeper BH mass functions, as they favor lower mass ratios that cause weaker recoils. For a steep enough mass function (β ≥ 1.5 for a random primary mass, and β ≥ 1 for a 104 M⊙ primary), significant SMBH growth is allowed for the fiducial escape velocity of ∼200 km s−1 as determined at the FFB phase for an exponential disk ignoring subsequent compaction events.
The bottleneck becomes more severe for a hot disk (θ = 0 − 30°). Here, with β = 1.5, and for m0 = 104 M⊙, the SMBH growing fraction becomes non-negligible only for Vesc > 350 km s−1. We find (not shown) that this threshold drops to ∼200 km s−1 once the primary exceeds 3 × 104 M⊙. We learn that in order to overcome the GW recoil bottleneck in a hot disk with a 104 M⊙ primary central BH the escape velocity should be boosted to the level of a few hundred km s−1, possibly by the compaction events that are expected to be common at the relevant redshifts.
A caveat of the current toy-model analysis is that it considers SMBH growth through a sequence of binary mergers, while the large number of BHs is likely to also lead to multiple merger chains, resulting in the growth of more than one SMBH. In such cases, large-recoil mergers of mass ratios > 0.1 are more likely, and the associated displacements of the central BH from the high-density core region would suppress its interaction with other sinking BHs and thus complicate the buildup of a single SMBH. This should be studied by non-trivial simulations that incorporate a proper treatment of multiple BH mergers.
6. Compaction-driven black hole growth
The SMBH growth is likely to be boosted by galactic wet compaction events, common at high redshifts, which affect both the BH inward migration rate estimated in Sect. 4 and the results of GW recoil discussed in Sect. 5.
The process of ‘wet compaction’ to a ‘blue nugget’ was introduced in Dekel & Burkert (2014) and Zolotov et al. (2015). The process and its far-reaching implications on all major galaxy properties were studied in these and in a series of subsequent papers, largely based on the VELA zoom-in cosmological simulations, and they are reviewed in Lapiner et al. (2023). According to the simulations, this is a generic process that occurred in the history of most galaxies, preferably when the DM halo reaches a “golden mass” of ∼1011.5 M⊙. Triggered by drastic angular-momentum loss, for example, due to wet galaxy mergers or collisions of counter-rotating inflowing streams, gas is pushed to the central region of the galaxy, where it causes a starburst. This results in a cuspy gas-rich ‘blue nugget’ that passively evolves to a compact stellar ‘red nugget’. This central mass concentration allows the formation of an extended gaseous disk by stabilizing it against inflow due to violent disk instability (Dekel et al. 2020). A similar picture, where the galaxies develop a baryon-dominated center once above a threshold stellar mass ∼109 M⊙ at all redshifts in the range z = 0 − 6, is confirmed based on the TNG50 simulations (de Graaff et al. 2025).
Lapiner et al. (2021), using the NewHorizon cosmological simulations which incorporated black holes, discussed the process of compaction-driven BH growth above the golden mass. They noticed that in pre-compaction galaxies of lower masses, the BHs tend to wander about the center, while post compaction they become confined to the galactic centers. This is interpreted as a result of the compaction-driven deepening of the central potential well and the enhancement of dynamical friction exerted on the BH by the dense central baryons.
The VELA, NewHorizon and TNG50 simulations allow a study of compaction events at z ∼ 6 and later; this specific redshift range may be an artifact of the low abundance of massive enough galaxies at higher redshifts in these simulations. In reality, compaction events might have occurred above a similar threshold mass at higher redshifts as well. We estimate that the typical FFB galaxies, that form at zffb ∼ 9, indeed reach the threshold mass for compaction by z ∼ 7, since a halo of ∼ 1011 M⊙ at zffb ∼ 9 is expected on average to grow by ∼1 dex until z ∼ 6 (assuming M ∝ e−0.8zDekel et al. 2013).
The compaction events can serve the SMBH growth in several ways. First, in cases where the disk-plus-halo density profile and the associated Ω(r) profile are too flat for efficient inward migration by dynamical friction, as discussed in Sect. 4, the steepening of these profiles by the wet compaction events may be necessary for ensuring continuing inward migration all the way to the galactic center, avoiding core stalling and possible buoyancy. Indeed, as can be seen in Fig. 24 of Lapiner et al. (2023), the post-compaction angular-velocity profile tends to be declining steeper than Ω(r) ∝ r−1 at all radii, typically enough for avoiding core stalling (Read et al. 2006; Goerdt et al. 2010; Kaur & Sridhar 2018; Dutta et al. 2019; Banik & van den Bosch 2021).
A second crucial role of the compaction events concerns overcoming the bottleneck introduced by the strong GW recoils of the SMBHs that result from misaligned spins and orbit of the merging BHs, as discussed in Sect. 5. By increasing the escape velocities from the galaxy centers, the compaction events may be important for breaking through this bottleneck, which can be non-trivial in the case of thick galactic disks. In the VELA zoom-in cosmological simulations, as seen in Fig. B1 of Lapiner et al. (2023), the post-compaction circular velocity within the effective radius Re ∼ 1 kpc is typically 250 km s−1, and it ranges from 160 km s−1 to 500 km s−1. Similarly, in the NewHorizon simulated galaxies with SMBHs, as seen in Fig. 4 of Lapiner et al. (2021), the post-compaction circular velocity at 1 kpc is typically 300 km s−1, and it ranges from 120 km s−1 to 500 km s−1. We can thus consider a typical post-compaction escape velocity of Vesc ∼ 350 km s−1, ranging from 170 to 700 km s−1. As found in Sect. 5, at the high end this is enough for keeping the SMBH at the galaxy center even in cases of misaligned spins and orbit in relatively thick disks.
Third, as discussed in Sect. 5.1, the wet compaction events can help solve the final parsec problem if triaxiality and three-body mergers fail to do so for a stellar system. The gas pushed into the galaxy center feeds an AGN accretion disk that can exert compressive circum-binary torques (Armitage & Natarajan 2002).
 |
Fig. 14. Cartoon summarizing the scenario of merger-driven BH growth in FFB galaxies at cosmic dawn. (a) Feedback-free starbursts in thousands of clusters at z ∼ 10, each forming in less than 3 Myr with a typical mass ∼106 M⊙, in ∼10 generations of ∼10 Myr each over a global FFB period of ∼100 Myr. (b) Rapid core collapse in each cluster during ∼3 Myr, sped up by the presence of massive stars and by cluster rotation and flattening, leading to a very massive central star (VMS) that becomes an intermediate-mass BH (IMBH) of ∼104 M⊙. (c) Tidal evaporation of the clusters, progressing inside-out in the galactic disk over ∼100 Myr, producing a background stellar disk capable of exerting effective dynamical friction. (d) dynamical-friction-driven inspiral of the BHs that accumulate at the galactic center total BH mass of ∼107 ± 1 M⊙ in ∼0.5 Gyr, namely by z ∼ 7. (e) SMBH growth by BH mergers, subject to GW recoils during the first stages of growth. The SMBH is retained if the galactic disk of BHs is cold or if the potential well is deepened by wet compaction events. |
As a word of caution we note that major galaxy mergers, one kind of the possible drivers of wet compaction events, may induce significant global morphological and kinematical changes in the structure of the galaxies that host the migrating BHs, and possibly add a mechanism of BH ejection. These effects are yet to be investigated. Another caveat is associated with the tendency of compaction events to occur near a ‘golden mass’ of ∼1010 M⊙ (Dekel et al. 2019; Lapiner et al. 2023). This introduces a potential difficulty for galaxies of much lower masses to retain post-merger over-massive BHs, in potential conflict with some of the low-mass BH hosts observed using JWST. For these low-mass galaxies to grow over-massive BHs by a merger-driven scenario, one has to appeal to the less frequent compaction events that occur below the golden mass. A third caveat associated with compaction events in the BH context is that they tend to lead to starbursts that increase the stellar mass (Tacchella et al. 2016b) and thus make it more difficult to obtain the required high values of fbh. This will have to be quantified using simulations that incorporate compaction events during the process of BH migration and mergers.
7. Conclusion
We verified the conditions under which the scenario of feedback-free starbursts at cosmic dawn (Dekel et al. 2023a; Li et al. 2024b) may provide a natural setting for the formation of intermediate-mass seed black holes and their subsequent growth, largely merger-driven, to super-massive black holes with a high BH-to-stellar mass ratio as indicated by JWST observations (Pacucci et al. 2023).
Figure 14 is a cartoon summarizing the main stages of the BH growth scenario that has been examined here. It starts with thousands of star clusters formed during the FFB phase within which rapid core collapse leads to intermediate-mass BH seeds. The FFB phase is followed by cluster disruption which causes the efficient inspiral of the BHs into the galactic center, where the BHs merge into a SMBH that may overcome GW recoil provided that the disk is cold or the potential well is deepened by wet compaction events.
In the FFB scenario, the sites for the formation of intermediate-mass seed black holes are the thousands of star clusters that serve as the building blocks of the FFB galaxies, each starbursting in a free-fall time of a few Myr during the lifetime of their massive stars and before the onset of stellar and supernova feedback. The seed black holes form by rapid core collapse in the FFB clusters (Lynden-Bell & Wood 1968) on a similar free-fall timescale, sped up by their young, broad stellar mass function. This process is further hastened by their internal rotation and associated spatial flattening in the disk version of the FFB scenario. The core collapse is driven by the inward migration of the short-lived massive stars due to the mass segregation by two-body interactions and dynamical friction, and it is sped up by the spatial flattening and the gravo-gyro instability (Hachisu 1979) that are induced by the cluster internal rotation within the galactic disks (Ceverino et al. 2012).
The FFB-generated seed BHs eventually migrate by dynamical friction to the centers of the compact galactic disks, ready to merge into SMBHs with high BH-to-stellar mass ratios. The dynamical friction is exerted mostly by the compact stellar galactic system that forms by the tidal disruption of the FFB clusters. The compact disk morphology in the disk version of the FFB scenario speeds up this dynamical friction process to the level required for matching the SMBH masses and high fbh ratios that are indicated by observations at z ∼ 4 − 7 as well as at z ∼ 1 − 3.
The SMBH growth by BH mergers has then to overcome the bottleneck introduced by GW recoil velocities that may exceed the escape velocity from the galaxy (Pretorius 2005; Campanelli et al. 2006; Baker et al. 2006). These recoil velocities can be large, especially during the first mergers where the BH mass ratio can be not much smaller than unity, and particularly so for large spin-orbit misalignments. A large fraction of growing SMBHs is nevertheless obtained for relatively cold disks of seed BHs.
The SMBH growth can be boosted up in three different ways by the generic wet compaction events that tend to occur at high redshifts above a threshold galaxy mass (Zolotov et al. 2015; Lapiner et al. 2023). First, the compaction-induced cuspy density profiles with steeply declining angular-velocity profiles could help avoide core stalling in the inward migration of BHs within the inner galactic disks. Second, the compaction events help overcome the GW recoil bottleneck by increasing the central escape velocities from the galaxies. Third, the push of gas into the galaxy center can help enable the final parsec approach of the merging BHs.
Our more quantitative conclusions are as follows:
-
For a standard IMF in rotating, flattened FFB clusters at z ∼ 10, BH seeds of ∼104 M⊙ (and smaller) are expected to form by core collapse in clusters of ∼106 M⊙ (and below), giving rise to particularly high BH-to-stellar mass ratios of fbh ∼ 0.01.
-
Such BHs are expected in most of the FFB clusters but not in the most massive clusters near the Toomre mass of ∼107 M⊙. However, with a very top-heavy IMF in disky, strongly rotating FFB clusters the core collapse could possibly be sped up to form ∼105 M⊙ BH seeds in the ∼107 M⊙ clusters.
-
Based on our estimate of the dynamical friction rate in an FFB compact galactic disk, most of the BH seeds of 104 M⊙ should migrate to the galaxy center and provide mass for a SMBH of ∼107 ± 1 M⊙ by z ∼ 4 − 7. Central SMBHs are thus capable of inheriting the high fbh ratio of ∼0.01, which originates in the process of runaway intermediate-mass BH formation in the FFB clusters, and matches observational estimates.
-
A significant fraction of the SMBHs can overcome the bottleneck introduced by GW recoils and grow by mergers once the seed BHs inspiral within a relatively cold galactic disk such that the spin-orbit misalignments are limited to 0 − 10° and the escape velocity is near the FFB fiducial value of ∼170 km s−1 or larger.
-
Wet compaction events are expected in galaxies once they grow above a threshold halo mass of Mv ∼ 1011.5 M⊙ (Lapiner et al. 2023). This steepens the decline of the central density profile and angular-velocity profile and thus suppresses potential core stalling of the inward migration of the BH seeds.
-
These compaction events typically increase the escape velocities to several hundred km s−1 and thus enable SMBH growth also in somewhat hotter disks of BH seeds, with spin-orbit misalignments of ∼30°. In addition, the supply of central gas can help overcome the final parsec problem in the BH mergers.
One should be aware that our current analysis is to be be interpreted with caution and serve primarily as a feasibility study because it is based on simplified modeling and involves large uncertainties. For example, in our idealized model the migrating BH seeds are assumed to coalesce into the SMBH, largely ignoring further growth of the BH by accretion of gas and stars. The seed BHs are assumed to keep their masses during the migration, ignoring binary BH mergers before coalescence in the center. The galaxy is very crudely assumed to remain static in time since the FFB phase ignoring galactic accretion and star formation at later times except for crudely considering the qualitative effects of wet compaction events.
There are rather surprising significant uncertainties in the basic physical processes that are involved in our crude modeling. One such uncertainty is associated with the gravo-thermal-gyro core-collapse time and the resultant intermediate-mass BH-seed mass within rotating, flattened clusters. The unknown width of the IMF adds to this uncertainty. A second severe uncertainty concerns the strength of dynamical friction in a disk, which governs the assembly to a SMBHs is the compact FFB galactic disks, and possibly also the core collapse in rotating disky clusters. Beyond their use in the current study, these two fundamental processes deserve detailed reliable numerical studies using N-body simulations that are currently missing from the literature.
The poorly constrained galactic disk morphology in the FFB phase introduces another uncertainty in the inward migration timescale, which may involve core stalling. In such cases, wet compaction events are necessary for allowing the completion of the migration process. Finally, the unknown flattening of the disk of inspiraling BHs and the wide range of possible escape velocities introduce an uncertainty in the ability of the merged SMBHs to survive GW recoils during the first mergers, as long as the SMBH has not grown significantly yet.
We considered here the minimum growth path of SMBHs by BH mergers, ignoring further SMBH growth by gas accretion. If the growth by mergers indeed dominates at high redshifts, it would evade the low-redshift Soltan (1982) relation. This relation is the observed consistency between the quasar luminosity density and one tenth of the SMBH mass energy density, which indicates that most SMBHs acquired the bulk of their mass through radiatively efficient AGN episodes associated with gas accretion. If the high-redshift SMBH growth is indeed mostly by mergers, the ratio between the AGN luminosity function and the SMBH volume density is expected to be lower than in lower-redshift quasars, and the SMBHs are expected to be of low X-ray luminosities, as observed. Furthermore, the AGN feedback is likely to be less effective, not intervening in the otherwise higher efficiencies of star formation predicted at high redshifts.
The encouraging results of our current feasibility study motivate a more quantitative study of the proposed scenario. The aim would be to verify the conditions under which mostly merger-driven BH growth atarting at the FFB phase at cosmic dawn can indeed lead to supermassive BHs as observed at cosmic morning, z ∼ 4 − 7.
Data and results underlying this article will be shared upon reasonable request to the corresponding author.
Acknowledgments
We are grateful for stimulating discussions with Martin Haehnelt, Thorsten Naab, Christophe Pichon, Priya Natarajan, Re’em Sari, Volker Springel and Marta Volonteri. This work was supported by the Israel Science Foundation Grants ISF 861/20 (AD, ZL), 2565/19 (NCS), 2414/23 (NCS), and 3061/21 (NM, ZL), by the Bi-national Science Foundation grants 2019772 (NCS), 2020397 (NCS), and 2020302 (NM), by the NSF-BSF grant 2023730 (AD), by the National Science Foundation grants AST-2307280 (FvdB) and AST-2407063 (FvdB), by an IASH postdoctoral fellowship (DDC), and by a Horizon-MSCA postdoctoral grant 101109759 (ZL).
References
- Alexander, T., & Natarajan, P. 2014, Science, 345, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Antwi-Danso, J. 2024, Nature, 629, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Natarajan, P. 2002, ApJ, 567, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Baker, J. G., Centrella, J., Choi, D.-I., Koppitz, M., & van Meter, J. 2006, Phys. Rev. Lett., 96, 111102 [NASA ADS] [CrossRef] [Google Scholar]
- Bañados, E., Venemans, B. P., Decarli, R., et al. 2016, ApJS, 227, 11 [Google Scholar]
- Banik, U., & van den Bosch, F. C. 2021, ApJ, 912, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Barausse, E., Morozova, V., & Rezzolla, L. 2012, ApJ, 758, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Faber, S. M., Perez-Gonzalez, P. G., et al. 2013, ApJ, 765, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Barro, G., Faber, S. M., Koo, D. C., et al. 2017, ApJ, 840, 47 [Google Scholar]
- Barth, A. J., Martini, P., Nelson, C. H., & Ho, L. C. 2003, ApJ, 594, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2023, MNRAS, 519, 688 [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [Google Scholar]
- Bekki, K. 2009, MNRAS, accepted [arXiv:0911.5461] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics (Princeton, NJ: Princeton Univ. Press) [Google Scholar]
- Blaes, O., Lee, M. H., & Socrates, A. 2002, ApJ, 578, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, L., & Loeb, A. 2008, MNRAS, 390, 1311 [NASA ADS] [Google Scholar]
- Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2024, Nat. Astron., 8, 126 [Google Scholar]
- Bonetti, M., Haardt, F., Sesana, A., & Barausse, E. 2018, MNRAS, 477, 3910 [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [Google Scholar]
- Cameron, A. J., Katz, H., Witten, C., et al. 2024, MNRAS, 534, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Campanelli, M., Lousto, C. O., Marronetti, P., & Zlochower, Y. 2006, Phys. Rev. Lett., 96, 111101 [CrossRef] [Google Scholar]
- Campanelli, M., Lousto, C., Zlochower, Y., & Merritt, D. 2007, ApJ, 659, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Ceverino, D., Dekel, A., Mandelker, N., et al. 2012, MNRAS, 420, 3490 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [Google Scholar]
- Cohn, H., & Kulsrud, R. M. 1978, ApJ, 226, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- de Graaff, A., Setton, D. J., Brammer, G., et al. 2025, Nat. Astron., 9, 280 [Google Scholar]
- Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [Google Scholar]
- Dekel, A., Devor, J., & Hetzroni, G. 2003, MNRAS, 341, 326 [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- Dekel, A., Zolotov, A., Tweed, D., et al. 2013, MNRAS, 435, 999 [Google Scholar]
- Dekel, A., Lapiner, S., & Dubois, Y. 2019, arXiv e-prints [arXiv:1904.08431] [Google Scholar]
- Dekel, A., Lapiner, S., Ginzburg, O., et al. 2020, MNRAS, 496, 5372 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Mandelker, N., Bournaud, F., et al. 2022, MNRAS, 511, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Sarkar, K. C., Birnboim, Y., Mandelker, N., & Li, Z. 2023a, MNRAS, 523, 3201 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Tziperman, O., Sarkar, K. C., et al. 2023b, MNRAS, 521, 4299 [NASA ADS] [CrossRef] [Google Scholar]
- Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Donner, K. J., & Sundelius, B. 1993, MNRAS, 265, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, Chowdhury D., van den Bosch, F. C., & van Dokkum, P. 2019, ApJ, 877, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Ernst, A., Glaschke, P., Fiestas, J., Just, A., & Spurzem, R. 2007, MNRAS, 377, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Wang, L., Tanikawa, A., Hirai, Y., & Saitoh, T. R. 2024, Science, 384, 1488 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [Google Scholar]
- Gerosa, D., & Kesden, M. 2016, Phys. Rev. D, 93, 124066 [NASA ADS] [CrossRef] [Google Scholar]
- Gerosa, D., Fumagalli, G., Mould, M., et al. 2023, Phys. Rev. D, 108, 024042 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., & Heggie, D. C. 1994, MNRAS, 268, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, O., Huertas-Company, M., Dekel, A., et al. 2021, MNRAS, 501, 730 [Google Scholar]
- Goerdt, T., Moore, B., Read, J. I., & Stadel, J. 2010, ApJ, 725, 1707 [Google Scholar]
- Gronke, M., Oh, S. P., Ji, S., & Norman, C. 2022, MNRAS, 511, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Grudić, M. Y., & Hopkins, P. F. 2023, Open J. Astrophys., submitted [arXiv:2308.16268] [Google Scholar]
- Guo, Y., Ferguson, H. C., Bell, E. F., et al. 2015, ApJ, 800, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Y., Rafelski, M., Bell, E. F., et al. 2018, ApJ, 853, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I. 1979, PASJ, 31, 523 [Google Scholar]
- Hachisu, I. 1982, PASJ, 34, 313 [NASA ADS] [Google Scholar]
- Haiman, Z., & Loeb, A. 2001, ApJ, 552, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Ouchi, M., Oguri, M., et al. 2023, ApJS, 265, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Fryer, C. L., Woosley, S. E., Langer, N., & Hartmann, D. H. 2003, ApJ, 591, 288 [CrossRef] [Google Scholar]
- Hirschi, R. 2007, A&A, 461, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoffman, L., & Loeb, A. 2007, MNRAS, 377, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Hofmann, F., Barausse, E., & Rezzolla, L. 2016, ApJ, 825, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, J., Kim, E., Lee, H. M., & Spurzem, R. 2013, MNRAS, 430, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Hernquist, L., et al. 2013, MNRAS, 430, 1901 [Google Scholar]
- Huertas-Company, M., Primack, J. R., Dekel, A., et al. 2018, ApJ, 858, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Huertas-Company, M., Guo, Y., Ginzburg, O., et al. 2020, MNRAS, 499, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., Visbal, E., & Haiman, Z. 2020, ARA&A, 58, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kamlah, A. W. H., Spurzem, R., Berczik, P., et al. 2022, MNRAS, 516, 3266 [CrossRef] [Google Scholar]
- Katz, H., Sijacki, D., & Haehnelt, M. G. 2015, MNRAS, 451, 2352 [Google Scholar]
- Kaur, K., & Sridhar, S. 2018, ApJ, 868, 134 [Google Scholar]
- Kim, E., Yoon, I., Lee, H. M., & Spurzem, R. 2008, MNRAS, 383, 2 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [Google Scholar]
- Kovács, O. E., Bogdán, Á., Natarajan, P., et al. 2024, ApJ, 965, L21 [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., & Muñoz, D. J. 2023, ARA&A, 61, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Lapiner, S., Dekel, A., & Dubois, Y. 2021, MNRAS, 505, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Lapiner, S., Dekel, A., Freundlich, J., et al. 2023, MNRAS, 522, 4515 [NASA ADS] [CrossRef] [Google Scholar]
- Le Tiec, A., Blanchet, L., & Will, C. M. 2010, CQG, 27, 012001 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Silverman, J. D., Shen, Y., et al. 2024a, ApJ, submitted [arXiv:2403.00074] [Google Scholar]
- Li, Z., Dekel, A., Sarkar, K. C., et al. 2024b, A&A, 690, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., Nayakshin, S., King, A. R., & Pringle, J. E. 2009, MNRAS, 398, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Loeb, A., & Rasio, F. A. 1994, ApJ, 432, 52 [Google Scholar]
- Lousto, C. O., Campanelli, M., Zlochower, Y., & Nakano, H. 2010, CQG, 27, 114006 [NASA ADS] [CrossRef] [Google Scholar]
- Lupton, R. H., & Gunn, J. E. 1987, AJ, 93, 1106 [Google Scholar]
- Lynden-Bell, D., & Wood, R. 1968, MNRAS, 138, 495 [NASA ADS] [Google Scholar]
- Madau, P., & Quataert, E. 2004, ApJ, 606, L17 [CrossRef] [Google Scholar]
- Magorrian, J., & Tremaine, S. 1999, MNRAS, 309, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Scholtz, J., Witstok, J., et al. 2024a, Nature, 627, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Scholtz, J., Curtis-Lake, E., et al. 2024b, A&A, 691, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelker, N., Dekel, A., Ceverino, D., et al. 2014, MNRAS, 443, 3675 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelker, N., Dekel, A., Ceverino, D., et al. 2017, MNRAS, 464, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, S. H., Federrath, C., & Krumholz, M. R. 2023, MNRAS, 521, 5160 [NASA ADS] [CrossRef] [Google Scholar]
- Menon, S. H., Lancaster, L., Burkhart, B. y., et al. 2024, ApJ, 967, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., & Milosavljević, M. 2005, Liv. Rev. Relat., 8, 8 [NASA ADS] [Google Scholar]
- Merritt, D., & Poon, M. Y. 2004, ApJ, 606, 788 [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Mezcua, M., Pacucci, F., Suh, H., Siudek, M., & Natarajan, P. 2024, ApJ, 966, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Milosavljević, M., & Merritt, D. 2003, ApJ, 596, 860 [Google Scholar]
- Mortlock, D. J., Warren, S. J., Venemans, B. P., et al. 2011, Nature, 474, 616 [Google Scholar]
- Natarajan, P., Pacucci, F., Ricarte, A., et al. 2024, ApJ, 960, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Pacucci, F., Nguyen, B., Carniani, S., Maiolino, R., & Fan, X. 2023, ApJ, 957, L3 [CrossRef] [Google Scholar]
- Perets, H. B., Li, Z., Lombardi, J. C., Jr., & Milcarek, S. R., Jr. 2016, ApJ, 823, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Pfister, H., Volonteri, M., Dubois, Y., Dotti, M., & Colpi, M. 2019, MNRAS, 486, 101 [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [Google Scholar]
- Portegies Zwart, S. F., Makino, J., McMillan, S. L. W., Hut, P. 1999, A&A, 348, 117 [NASA ADS] [Google Scholar]
- Portegies Zwart, S. F., Baumgardt, H., Hut, P., Makino, J., McMillan, S. L. W. 2004, Nature, 428, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Pretorius, F. 2005, Phys. Rev. Lett., 95, 121101 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, P. J., & Goodman, J. 1986, ApJ, 309, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Rantala, A., Naab, T., & Lahén, N. 2024, MNRAS, 531, 3770 [NASA ADS] [CrossRef] [Google Scholar]
- Read, J. I., Goerdt, T., Moore, B., et al. 2006, MNRAS, 373, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1988, Nature, 333, 523 [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzuto, F. P., Naab, T., Spurzem, R., et al. 2021, MNRAS, 501, 5257 [NASA ADS] [CrossRef] [Google Scholar]
- Rizzuto, F. P., Naab, T., Rantala, A. i., et al. 2023, MNRAS, 521, 2930 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, T., Perna, R., Haiman, Z., Ostriker, J. P., & Stone, N. C. 2018, MNRAS, 473, 3410 [Google Scholar]
- Schleicher, D. R. G., Reinoso, B., Latif, M., et al. 2022, MNRAS, 512, 6192 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, R., Ferrara, A., Natarajan, P., & Omukai, K. 2002, ApJ, 571, 30 [CrossRef] [Google Scholar]
- Schnittman, J. D., Buonanno, A., van Meter, J. R., et al. 2008, Phys. Rev. D, 77, 044031 [NASA ADS] [CrossRef] [Google Scholar]
- Sijacki, D., Springel, V., & Haehnelt, M. G. 2009, MNRAS, 400, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A., Baumgardt, H., & Hilker, M. 2019, MNRAS, 485, 1460 [Google Scholar]
- Soltan, A. 1982, MNRAS, 200, 115 [Google Scholar]
- Spitzer, L., Jr., & Hart, M. H. 1971, ApJ, 164, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Pakmor, R., Zier, O., & Reinecke, M. 2021, MNRAS, 506, 2871 [NASA ADS] [CrossRef] [Google Scholar]
- Steinhardt, C. L., Kokorev, V., Rusakov, V., Garcia, E., & Sneppen, A. 2023, ApJ, 951, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, G. R., & Ida, S. 2000, Icarus, 143, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, N. C., Küpper, A. H. W., & Ostriker, J. P. 2017, MNRAS, 467, 4180 [NASA ADS] [Google Scholar]
- Tacchella, S., Dekel, A., Carollo, C. M., et al. 2016a, MNRAS, 458, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Dekel, A., Carollo, C. M., et al. 2016b, MNRAS, 457, 2790 [Google Scholar]
- Tacchella, S., McClymont, W., Scholtz, J., et al. 2024, MNRAS, submitted [arXiv:2404.02194] [Google Scholar]
- Tomassetti, M., Dekel, A., Mandelker, N., et al. 2016, MNRAS, 458, 4477 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Tremaine, S., & Weinberg, M. D. 1984, MNRAS, 209, 729 [Google Scholar]
- Trujillo-Gomez, S., Reina-Campos, M., & Kruijssen, J. M. D. 2019, MNRAS, 488, 3972 [NASA ADS] [CrossRef] [Google Scholar]
- Übler, H., Maiolino, R., Curtis-Lake, E., et al. 2023, A&A, 677, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valtonen, M. J., Valtaoja, L., Sundelius, B., Donner, K. J., & Byrd, G. G. 1990, Celest. Mech. Dyn. Astron., 48, 95 [Google Scholar]
- van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E. 2019, MNRAS, 482, 1525 [Google Scholar]
- Vasiliev, E., Antonini, F., & Merritt, D. 2015, ApJ, 810, 49 [Google Scholar]
- Volonteri, M. 2010, A&ARv, 18, 279 [Google Scholar]
- Weibel, A., de Graaff, A., Setton, D. J., et al. 2024, ApJ, submitted [arXiv:2409.03829]. [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Genzel, R., et al. 2012, ApJ, 753, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Yung, L. Y. A., Somerville, R. S., Finkelstein, S. L., Wilkins, S. M., & Gardner, J. P. 2024, MNRAS, 527, 5929 [Google Scholar]
- Yungelson, L. R., van den Heuvel, E. P. J., Vink, J. S., Portegies, Zwart S. F., & de Koter A., 2008, A&A, 477, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, D. H., Jing, Y. P., Mo, H. J., & Börner, G. 2009, ApJ, 707, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Zolotov, A., Dekel, A., Mandelker, N., et al. 2015, MNRAS, 450, 2327 [Google Scholar]
All Figures
 |
Fig. 1. Black hole mass versus stellar mass as estimated from observations. Shown is the bias-corrected relation at z = 4 − 7 as derived by Pacucci et al. (2023) (red shading, ±1σ scatter). It is based on the data from JWST marked by the symbols (JADES, CEERS and GA-NIFS Maiolino et al. 2024b; Harikane et al. 2023; Übler et al. 2023). Also shown are data at z = 1 − 3 (Mezcua et al. 2024). The high-z relation is compared to the local relation by Reines & Volonteri (2015) (green shading). The typical values of fbh at z = 4 − 7 are higher than the local relation by > 3σ, a factor of 10 − 100. |
| In the text | |
 |
Fig. 2. Black hole growth in non-rotating FFB clusters with a broad IMF. Shown is the cluster half-mass radius versus mass. The magenta curves and regions below them refer to clusters where core collapse occurs within 3 Myr, the lifetime of massive stars. Left: based on Eq. (4) (Portegies Zwart & McMillan 2002; Devecchi & Volonteri 2009), assuming either ⟨m⟩ = 10 M⊙ (solid) or ⟨m⟩ = 100 M⊙ (dashed). Right: based on Eq. (3) (Rizzuto et al. 2021, Eq. (4)), assuming mmax = 100 (solid) or 300 M⊙ (dashed). The blue and red lines refer to constant density n = 103.5 cm−3 and surface density Σ = 103.5 M⊙ pc−2 within the half-mass radius. Feedback-free starbursts are expected to occur near such densities. FFB clouds of the Jeans mass and radius, ∼106 M⊙ and ∼7 pc, lie above the core-collapse line, though not too far away if the IMF is very top-heavy, of a population-III.1 type, with ⟨m⟩ ∼ 100 M⊙ (left) or mmax > 300 M⊙ (right). If the sub-Jeans clouds form by fragmentation with the same Σ, they should lie along the red line, such that core collapse will occur in 3 Myr for Mc ≤ 105 M⊙ and Re ≤ 2 pc. The corresponding black-hole mass at the end of the FFB phase, Eq. (5), in addition to the initial mass of the massive star that became the VMS, is marked in the top axis, indicating Mbh ∼ 103 M⊙ in ∼105 M⊙ clusters. |
| In the text | |
 |
Fig. 3. Distribution of rotation support, |
| In the text | |
 |
Fig. 4. Black hole growth in rotating FFB clusters with a broad IMF. Same as Fig. 2, right panel, based on Eq. (3) (Rizzuto et al. 2021, Eq. (4)), but with tcc reduced by a factor of 10 due to rotation (gravo-gyro instability; Hachisu 1979, 1982; Hong et al. 2013; Kamlah et al. 2022) and flattening. The FFB clouds that form by disk instability at the characteristic Toomre mass of ∼107 M⊙ (Dekel et al. 2023a), lie above the curve (magenta) that marks core-collapse in 3 Myr. However, if sub-Toomre clouds form by fragmentation with the same Σ, they should lie along the red line, such that core collapse will occur in 3 Myr for Mc ≤ 106 M⊙. The corresponding black-hole mass at the end of the FFB phase, Eq. (5), is Mbh ≤ 104 M⊙ (top axis). |
| In the text | |
 |
Fig. 5. N-body simulation of post-FFB cluster disruption and the buildup of a smooth stellar disk component capable of exerting dynamical friction on the BHs of each cluster. Shown is the projected stellar distribution in one quadrant of the galactic plane, in a slice of thickness ±50 pc, at different times. One thousand star particles are selected at random from each cluster. The colors represent radial distance at t = 0. The clusters survive mostly intact for a few tens of Myr, namely several cluster free-fall times, allowing FFB and core collapse to seed BHs in them. A significant smooth component is building inside-out to become dominant by ∼100 Myr, after a few galactic orbital times. |
| In the text | |
 |
Fig. 6. Buildup of the smooth stellar disk component. The presence of clusters is measured by the standard deviation of the density fluctuation σδ in the disk plane near radius r at time t. The density is measured in pixels of side 30 pc, comparable to the original cluster size. The smooth component becomes significant, with σδ < 1, after ∼10 Myr, a few FFB cluster free-fall times, and before ∼100 Myr, several galactic orbital times. |
| In the text | |
 |
Fig. 7. Testing the inward migration by dynamical friction in a disk. The solid curves refer to N-body simulations of a BH of mass m starting in a circular orbit at ri within a thin live Mestel disk with an isothermal halo as an external potential. The left and right panels refer to ri = 0.07R0 and 0.1R0. Shown for comparison are analytic estimates based on Eq. (21) (dotted) and Eq. (22) (dashed), crudely normalized for best overall fit in the four cases. We learn from this comparison that the analytic approximations are realistic conservative estimates. |
| In the text | |
 |
Fig. 8. Supermassive BH mass (left) and BH-to-stellar mass ratio (right) as a function of redshift for zffb = 9 (blue) and 12 (magenta), with m = 104 M⊙. This is either in a hot disk (Eq. (19), solid) or in a cold disk (Eq. (21), long-dashed). The FFB-threshold halo properties as a function of zffb are from Eqs. (24) and (25) (Dekel et al. 2023a). The SFE is ϵ = 0.2. The BHs are assumed to be on circular orbits responding to DF from the stellar disk (V/σ = 5) plus an NFW DM halo (whose contribution is negligible, short dashed). The BHs are assumed to start in an exponential disk whose radius is estimated in Eq. (27) (Li et al. 2024b). The galaxy stellar mass, assumed to be constant in time, is marked (dotted). The 1σ scatter due to the scatter in disk size in Eq. (27) is ±0.2 dex. Eddington growth is marked for comparison (thin dashed green) The observational estimates are shown for comparison. The data are from Maiolino et al. (2024b) (circles), Harikane et al. (2023) and Übler et al. (2023) (squares). The selection-bias-corrected mean and standard deviation by (Pacucci et al. 2023) based on the data in red symbols are marked by the red lines. The values of fbh at z = 4 − 7 are > 3σ above the standard z = 0 low-z ratio by Reines & Volonteri (2015) (indicated by dashed green lines). The average SMBH masses and fbh ratios as deduced from the observations at z ∼ 4 − 7 are reproduced by the 104 M⊙ seeds of the FFB scenario. |
| In the text | |
 |
Fig. 9. Scatter in SMBH mass. Same as Fig. 8 but for zffb = 10 and for three caes: Middle, blue: the fiducial case, with ϵ = 0.2, halo mass at the FFB threshold, and seed BHs of m = 104 M⊙, is recovering the average BH mass at z = 4 − 7. Top, magenta: with ϵ = 1 and halo mass 3x the FFB threshold, the model reproduces the most massive BHs at z = 4 − 7. Bottom, green: with seed BHs of m = 103 M⊙, the BH growth in a hot disk is not sufficiently fast. |
| In the text | |
 |
Fig. 10. Recoil velocity of the merged BH due to a merger between two BHs as a function of their mass ratio q = m2/m1. The cases shown are (i) non-spinning BHs (red), (ii) a strongly spinning BH a1 = 0.9 where the spin is aligned with the orbit (blue), (iii) strongly spinning BHs a1 = a2 = 0.9 (with respect to the maximum possible a1 = 1) with the spins aligned with the orbit (magenta), and (iv) a strongly spinning BH a1 = 0.9 with the spin inclined at 10° or at 30° with respect to orbit, spanning the full range of phases for the encounter (diagonal lines area and shaded area, respectively). Marked in comparison are the fiducial and maximum escape velocities from an FFB galactic disc of 171 and 700 km s−1 (black dashed, gray dashed). |
| In the text | |
 |
Fig. 11. Negative slope β of the mass function of BH seeds as they merge with the central SMBH, ψ ∝ m−β. It is derived using Eq. (42) assuming an original BH mass function ϕ ∝ m−2 everywhere in the disk, a disk of BHs with a power-law surface density profile Σ ∝ r−γ, and a total circular velocity Vc ∝ rμ (which may include the additional contribution of a halo and a post-compaction central mass). At time t and mass m, these two power laws are relevant for the radial region from which BHs of mass m arrive to the center at time t, as derived for a hot disk using tdf = 0.5Vc/adf and adf from Eq. (19). Self-gravitating disks with the shown μ are marked by red circles. We read, for example, that for a flat rotation curve (μ = 0) and for the BHs that arrive from the disk range where Σ ∝ r−1 (a self-gravitating Mestel disk) the mass function at the center is ψ ∝ m−1.5. These values of β refer to the mass function used in the recoil simulations summarized in Fig. 13. |
| In the text | |
 |
Fig. 13. Simulation results for the the GW recoil bottleneck. Shown is the threshold escape velocity Vesc that is required for SMBH growth in at least one third of the cases as a function of the slope β of the BH mass-function ψ ∝ m−β. The blue lower curves are for cold disks, with spin-orbit misalignments θ = 0 − 10°, while the red upper curves correspond to hot disks, with θ = 0 − 30°. The solid and dashed curves refer to cases where the mass of the initial primary BH m0 is either drawn from the seed BH mass function in (102 − 104 M⊙) or selected to be 104 M⊙, respectively. The fiducial escape velocity for an FFB disk at zffb = 9 is Vesc ≃ 170 km s−1 when ignoring compaction events, and it could rise to several hundred km s−1 after compaction (horizontal dotted lines). Naturally, the required escape velocity for BH growth is lower for a steeper BH mass function. For no BH spins, or fully aligned spin and orbit, there is always growth for Vesc ≥ 100 km s−1 (not shown). For a cold disk, The fiducial Vesc ∼ 200 km s−1 of FFB is sufficient for BH growth if β ≥ 1.5 (or β ≥ 1) for a random m0 (or m0 = 104 M⊙). The bottleneck becomes more severe for a hot disk, where a non-negligible growing fraction can be obtained either with a Vesc that has been boosted by compaction events to the level of a few hundred km s−1, or with the original FFB Vesc ∼ 200 km s−1 if m0 > 3 × 104 M⊙ (not shown). |
| In the text | |
 |
Fig. 12. Growth of supermassive BH by mergers in four simulations of one example case, where the initial primary mass is drawn from the BH mass function of β = 1.13, the spin-orbit misalignment angle is randomly drawn from 0 − 10°, and Vesc = 200 km s−1. The sequence of mergers is represented along the x axis by the accumulated mass of the merging BHs from the initial primary mass to a total of 107 M⊙. Top left: the mass of the merged BH after each merger. Top right: the recoil velocity in comparison to the escape velocity. Bottom left: the mass ratio (when it is larger than unity, the primary and secondary exchange roles). Bottom right: the spin of the primary BH. When Vrecoil > Vesc the SMBH is ejected and a new primary is chosen. This is more likely to happen in the early mergers, when the mass ratio tends to be high. Three of the SMBHs manage to eventually grow while one fails (blue). Growth is practically guaranteed once the SMBH mass exceeds 105 M⊙, while the secondary merging BHs are limited to ≤104 M⊙ such that the mass ratio drops below 0.1. |
| In the text | |
 |
Fig. 14. Cartoon summarizing the scenario of merger-driven BH growth in FFB galaxies at cosmic dawn. (a) Feedback-free starbursts in thousands of clusters at z ∼ 10, each forming in less than 3 Myr with a typical mass ∼106 M⊙, in ∼10 generations of ∼10 Myr each over a global FFB period of ∼100 Myr. (b) Rapid core collapse in each cluster during ∼3 Myr, sped up by the presence of massive stars and by cluster rotation and flattening, leading to a very massive central star (VMS) that becomes an intermediate-mass BH (IMBH) of ∼104 M⊙. (c) Tidal evaporation of the clusters, progressing inside-out in the galactic disk over ∼100 Myr, producing a background stellar disk capable of exerting effective dynamical friction. (d) dynamical-friction-driven inspiral of the BHs that accumulate at the galactic center total BH mass of ∼107 ± 1 M⊙ in ∼0.5 Gyr, namely by z ∼ 7. (e) SMBH growth by BH mergers, subject to GW recoils during the first stages of growth. The SMBH is retained if the galactic disk of BHs is cold or if the potential well is deepened by wet compaction events. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



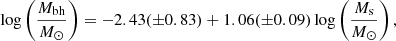
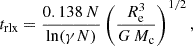
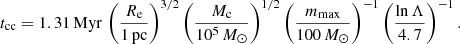
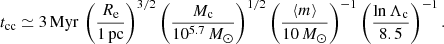
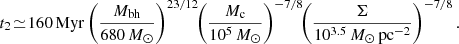
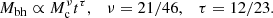
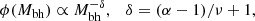
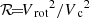
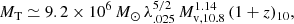
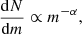
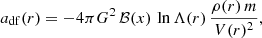
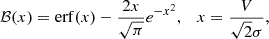
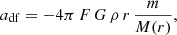
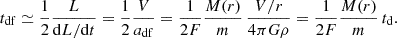
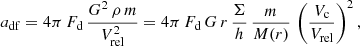
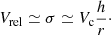
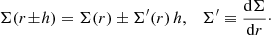
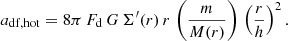
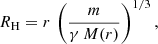
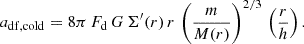
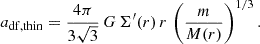
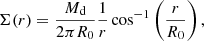
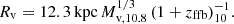
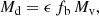
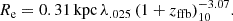
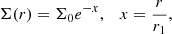
![$$ \begin{aligned} M_{\rm d}(r) = M_{\rm d}[1-e^{-x}(x+1)],\quad M_{\rm d}= 2\pi r_1^2 \Sigma _0. \end{aligned} $$](/articles/aa/full_html/2025/03/aa52393-24/aa52393-24-eq33.gif)
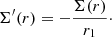
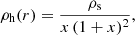
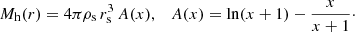
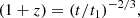
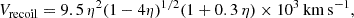
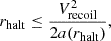
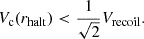
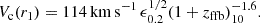
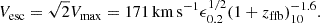
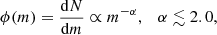
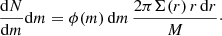
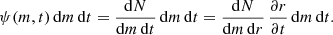
![$$ \begin{aligned} \psi (m,t) = \phi (m)\, \frac{2\pi \, \Sigma [r(m,t)]\, r(m,t)}{M}\, \frac{\partial r(m,t)}{\partial t}\cdot \end{aligned} $$](/articles/aa/full_html/2025/03/aa52393-24/aa52393-24-eq50.gif)