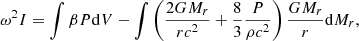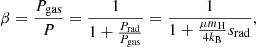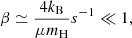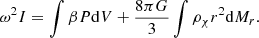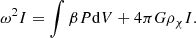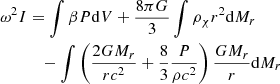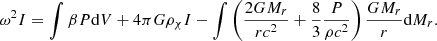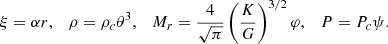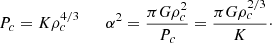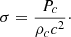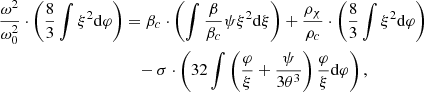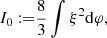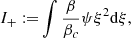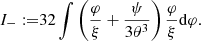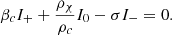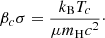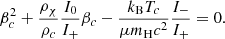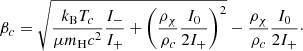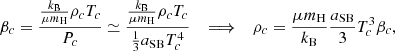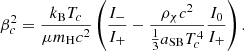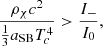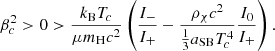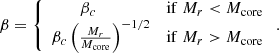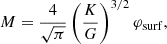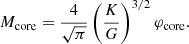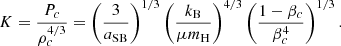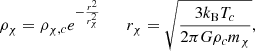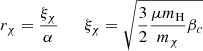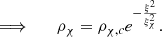EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 689 (September 2024) A&A, 689 (2024) A202 Full HTML
Open Access
Issue
A&A
Volume 689, September 2024
Article Number A202
Number of page(s) 7
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202450484
Published online 13 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Supermassive black hole (SMBH) formation is currently one of the most challenging open problems in astronomy (e.g. Woods et al. 2019; Haemmerlé et al. 2020). At redshifts z ≳ 7, a number of SMBHs with masses M• ≳ 109 M⊙ have been detected in the last decade (e.g. Wu et al. 2015; Bañados et al. 2018; Yang et al. 2020; Wang et al. 2021), which implies average accretion rates above 1 M⊙ yr−1. Such rapid mass growths are in tension with the scenario of an initial seed provided by the collapse of a ∼100 M⊙ star (e.g. Wang et al. 2021), and point towards the direct collapse scenario, which is the direct formation of a seed with M• ∼ 105 − 107 M⊙ from the monolithic collapse of gas at galactic scales (e.g. Rees 1978). This tension is reinforced by the recent discoveries made with the James Webb Space Telescope at higher redshifts, for instance GN-z11 (z = 11, M• ∼ 106 M⊙, Maiolino et al. 2024), UHZ1 (z = 10.3, M• ∼ 4 × 107 M⊙, Bogdán et al. 2024), and GHZ 9 (z ≃ 10, M• ∼ 0.5 − 1 × 108 M⊙, Kovács et al. 2024). Interestingly, the masses of these objects correspond to those of seeds generated by direct collapse, while no SMBH is found with a mass below those allowed by this scenario (Maiolino et al. 2023; Andika et al. 2024).

Direct collapse implies the existence of supermassive stars (SMSs) with masses > 104 M⊙ (e.g. Fowler 1966; Baumgarte & Shapiro 1999; Hosokawa et al. 2013; Shibata et al. 2016; Umeda et al. 2016; Woods et al. 2017, 2020, 2021; Woods et al. 2024; Haemmerlé et al. 2018a,b, 2019, 2020, 2021a; Nagele et al. 2022, 2023a,b; Nagele & Umeda 2023; Herrington et al. 2023; Nandal et al. 2023) and their eventual collapse via the general-relativistic (GR) instability (Chandrasekhar 1964). Two channels of direct collapse have been considered in the literature. The first is the collapse of a primordial atomically cooled halo (e.g. Haiman et al. 1997; Omukai 2001; Dijkstra et al. 2008; Bromm & Loeb 2003; Latif et al. 2013; Regan et al. 2017; Chon et al. 2018), in which a Population III (Pop III) SMS forms under accretion rates 0.01–1 M⊙ yr−1; the second channel is the mergers of massive gas-rich galaxies (Mayer et al. 2010, 2015, 2024), triggering inflows of 100–1000 M⊙ yr−1 down to subparsec scales, and resulting potentially in the formation of a Population I (Pop I) SMS (Haemmerlé et al. 2019, 2021; Zwick et al. 2023).

Without dark matter, the mass of the black hole seed, given essentially by the final mass of the progenitor SMS at collapse, belongs to distinct ranges in these two scenarios (Haemmerlé 2020, 2021a): 105 M⊙ ≲ M ≲ 106 M⊙ in atomically cooled halos; M > 106 M⊙ in galaxy mergers. On the other hand, the presence of a dark matter background has been shown to delay the GR instability via its gravitational field, in the case of polytropic models (McLaughlin & Fuller 1996; Bisnovatyi-Kogan 1998; Kehrer & Fuller 2024). However, polytropic SMSs correspond to isentropic thermally relaxed structures, which stands in conflict with accretion at rates ≳ 0.1 M⊙ yr−1 (Hosokawa et al. 2013; Umeda et al. 2016; Woods et al. 2017; Haemmerlé et al. 2018a, 2019). For such accretion rates, the structure is better approximated by hylotropes (Begelman 2010; Haemmerlé 2020, 2021a), made of a convective isentropic core and a radiative envelope. Moreover, as pointed out by Bisnovatyi-Kogan (1998), the stabilisation of a polytropic SMS by the gravitational field of a dark matter background requires unrealisticly high densities of dark matter (≳0.001 g cm−3). Models of adiabatic contraction for star formation indicate ambient dark matter densities ≲10−10 g cm−3 in protostars (Freese et al. 2009). On the other hand, if dark matter is made of weakly interacting massive particles (WIMPs), the densities can be increased by orders of magnitude, thanks to the interactions with the baryonic gas that capture the dark matter particles in the gravitational potential well of the star (Spolyar et al. 2008; Taoso et al. 2008, 2010; Freese et al. 2010; Kouvaris & Tinyakov 2011; Ellis 2022). In this case, the captured dark matter component converges to a highly centralised thermal density profile 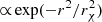∝exp(− r 2 / r χ 2 ) $ {\propto}\exp(-r^2/r_\chi^2) $ (Taoso et al. 2008). Moreover, WIMPs being Majorana particles; they are their own antiparticles and can annihilate to convert their mass (in the range 1 GeV–10 TeV, typically 100 GeV) into thermal energy. For efficient enough capture, the energetic input from WIMP annihilation is found to prevent the contraction of stars before H-burning ignition (Spolyar et al. 2008; Taoso et al. 2008; Freese et al. 2010), favouring low densities of baryonic gas and low central temperatures. Models of SMSs fuelled by WIMP annihilation indicate that the central temperature is kept down to 106 − 107 K for objects of 105 − 107 M⊙, in contrast with the ∼108 K given by H-burning. In this picture, WIMP annihilation limits the accumulation of dark matter in the star’s core, avoiding catastrophic collapse (in contrast with Kouvaris & Tinyakov 2011; Ellis 2022). We also find, in the case of energetically significant WIMP annihiliation, that the low central temperature translates into a reduction of the neutrino emission studied in Kehrer & Fuller (2024).

For the present work, we studied how dark matter impacts the maximum mass of SMSs consistent with GR dynamical stability. We applied the post-Newtonian method of McLaughlin & Fuller (1996) to the full range of hylotropes, considering both homogeneous and 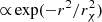∝exp(− r 2 / r χ 2 ) $ {\propto}\exp(-r^2/r_\chi^2) $ density profiles for the dark matter component in order to determine the impact of the dark matter gravitational field on the GR stability of SMSs. We considered the central temperatures given by H-burning, as well as those imposed by energetically significant WIMP annihilation. The method is presented in Sect. 2; the results are described in Sect. 3 and discussed in Sect. 4; we conclude in Sect. 5.

2. Method

2.1. GR instability

A sufficient condition for GR instability can be obtained from the relativistic equation of adiabatic pulsations (e.g. Chandrasekhar 1964; Fowler 1966; Fuller et al. 1986; Haemmerlé 2021b; Feng 2023). This criterion is based on a mathematical proof by Chandrasekhar (1964), with the same GR ingredients used in numerical stellar models. SMSs are always close to the Newtonian and Eddington limits, and in this case the criterion for instability reads ω2 < 0 with (Haemmerlé 2021a)

ω 2 I = ∫ β P d V − ∫ ( 2 G M r r c 2 + 8 3 P ρ c 2 ) G M r r d M r , $$ \begin{aligned} \omega ^2I=\int \beta P\mathrm{d} V-\int \left({2GM_r\over rc^2}+{8\over 3}{P\over \rho c^2}\right){GM_r\over r}\mathrm{d} M_r ,\end{aligned} $$(1)

where r is the radial coordinate, Mr the mass-coordinate, P the pressure, β the ratio of gas to total pressure, ρ the density of mass, dV a volume element, I the moment of inertia, G the gravitational constant, and c the speed of light. The ratio β is related to the entropy of radiation srad by

β = P gas P = 1 1 + P rad P gas = 1 1 + μ m H 4 k B s rad , $$ \begin{aligned} \beta ={P_{\rm gas}\over P}={1\over 1+{P_{\rm rad}\over P_{\rm gas}}}={1\over 1+{\mu m_{\rm H}\over 4 k_{\rm B}}s_{\rm rad}} ,\end{aligned} $$(2)

where kB is the Boltzmann constant, mH the mass of a baryon and μ the mean molecular weight. Because of the proximity with the Eddington limit, it is well approximated by

β ≃ 4 k B μ m H s − 1 ≪ 1 , $$ \begin{aligned} \beta \simeq {4k_{\rm B}\over \mu m_{\rm H}}s^{-1}\ll 1 ,\end{aligned} $$(3)

where s ≃ srad is the total specific entropy.

In this post-Newtonian approximation, distinctions between relativistic mass and rest mass can be neglected. Moreover, criterion (1) becomes an exact condition (Chandrasekhar 1964). Dynamical simulations in full GR indicate the instability slightly earlier (Nagele et al. 2022), but the discrepancies remain in the range of second-order post-Newtonian corrections.

On the other hand, if we account for a dark matter component with density ρχ ≪ ρ, interacting with the star via gravitation only without following the stellar pulsations, a Newtonian pulsation analysis gives (McLaughlin & Fuller 1996)

ω 2 I = ∫ β P d V + 8 π G 3 ∫ ρ χ r 2 d M r . $$ \begin{aligned} \omega ^2I=\int \beta P\mathrm{d} V+{8\pi G\over 3}\int \rho _\chi r^2\mathrm{d} M_r .\end{aligned} $$(4)

If the dark matter distribution is homogeneous, Equation (4) becomes

ω 2 I = ∫ β P d V + 4 π G ρ χ I . $$ \begin{aligned} \omega ^2I=\int \beta P\mathrm{d} V+4\pi G\rho _\chi I .\end{aligned} $$(5)

We see that dark matter stabilises the star via a positive term in the pulsation equation. If a Lagrangian layer contracts slightly from its equilibrium position, the decrease in the enclosed mass corresponding to the dark matter component will reduce the gravity on this layer and favour the restoring force. Thus, the assumption that dark matter does not follow the pulsations corresponds to the case where its stabilising effects are the strongest. If dark matter follows the pulsations, it behaves like baryonic gas, and can be neglected in the dynamical stability since ρχ ≪ ρ. We note that we do not account for the eventual instability of the dark matter component itself; in particular, we do not consider the possibility of a runaway contraction of dark matter, in contrast with Kouvaris & Tinyakov (2011) and Ellis (2022): our treatment focuses on the GR instability of the baryonic gas.

As long as the GR corrections for the gas remain small, and as long as ρχ ≪ ρ, the GR corrections for dark matter are negligible compared to the Newtonian dark matter term and the post-Newtonian term for gas (McLaughlin & Fuller 1996; Bisnovatyi-Kogan 1998). In this case, the combined effect of GR corrections and dark matter is well captured by

ω 2 I = ∫ β P d V + 8 π G 3 ∫ ρ χ r 2 d M r − ∫ ( 2 G M r r c 2 + 8 3 P ρ c 2 ) G M r r d M r $$ \begin{aligned} \omega ^2I&=\int \beta P\mathrm{d} V+{8\pi G\over 3}\int \rho _\chi r^2\mathrm{d} M_r \\ &\quad -\int \left({2GM_r\over rc^2}+{8\over 3}{P\over \rho c^2}\right){GM_r\over r}\mathrm{d} M_r \end{aligned} $$(6)

or, for homogeneous dark matter distribution:

ω 2 I = ∫ β P d V + 4 π G ρ χ I − ∫ ( 2 G M r r c 2 + 8 3 P ρ c 2 ) G M r r d M r . $$ \begin{aligned} \omega ^2I=\int \beta P\mathrm{d} V+4\pi G\rho _\chi I-\int \left({2GM_r\over rc^2}+{8\over 3}{P\over \rho c^2}\right){GM_r\over r}\mathrm{d} M_r .\end{aligned} $$(7)

This equation can be re-expressed in dimensionless form by defining the following dimensionless functions:

ξ = α r , ρ = ρ c θ 3 , M r = 4 π ( K G ) 3 / 2 φ , P = P c ψ . $$ \begin{aligned} \xi =\alpha r, \quad \rho =\rho _c\theta ^3, \quad M_r={4\over \sqrt{\pi }}\left({K\over G}\right)^{3/2}\varphi , \quad P=P_c\psi . \end{aligned} $$(8)

The constants K and α, which give respectively the mass scales and length scales, are defined from the central pressure and density by

P c = K ρ c 4 / 3 α 2 = π G ρ c 2 P c = π G ρ c 2 / 3 K · $$ \begin{aligned} P_c=K\rho _c^{4/3} \qquad \alpha ^2={\pi G\rho _c^2\over P_c}={\pi G\rho _c^{2/3}\over K}\cdot \end{aligned} $$(9)

We define the following parameter for the GR corrections:

σ = P c ρ c c 2 · $$ \begin{aligned} \sigma ={P_c\over \rho _c c^2}\cdot \end{aligned} $$(10)

With these definitions, Equation (7) reads

ω 2 ω 0 2 · ( 8 3 ∫ ξ 2 d φ ) = β c · ( ∫ β β c ψ ξ 2 d ξ ) + ρ χ ρ c · ( 8 3 ∫ ξ 2 d φ ) − σ · ( 32 ∫ ( φ ξ + ψ 3 θ 3 ) φ ξ d φ ) , $$ \begin{aligned} {\omega ^2\over \omega _0^2}\cdot \left({8\over 3}\int \xi ^2\mathrm{d}\varphi \right)&=\beta _c\cdot \left(\int {\beta \over \beta _c}\psi \xi ^2\mathrm{d}\xi \right) +{\rho _\chi \over \rho _c}\cdot \left({8\over 3}\int \xi ^2\mathrm{d}\varphi \right) \nonumber \\&\quad -\sigma \cdot \left(32\int \left({\varphi \over \xi }+{\psi \over 3\theta ^3}\right){\varphi \over \xi }\mathrm{d}\varphi \right) ,\end{aligned} $$(11)

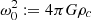with ω 0 2 :=4πG ρ c $ \omega_0^2:=4\pi G\rho_c $, where βc is the value of β at the centre of the star. Each term of Equation (11) is made of an integral that involves only the dimensionless functions (8), to which we add β/βc for β:

I 0 : = 8 3 ∫ ξ 2 d φ , $$ \begin{aligned} I_0:=&{8\over 3}\int \xi ^2\mathrm{d}\varphi ,\end{aligned} $$(12)

I + : = ∫ β β c ψ ξ 2 d ξ , $$ \begin{aligned} I_+:=&\int {\beta \over \beta _c}\psi \xi ^2\mathrm{d}\xi ,\end{aligned} $$(13)

I − : = 32 ∫ ( φ ξ + ψ 3 θ 3 ) φ ξ d φ . $$ \begin{aligned} I_-:=&32\int \left({\varphi \over \xi }+{\psi \over 3\theta ^3}\right){\varphi \over \xi }\mathrm{d}\varphi .\end{aligned} $$(14)

Each integral is scaled by a dimensionless parameter: βc expresses the departures from the Eddington limit, σ the departures from the Newtonian limit, and ρχ/ρc the presence of dark matter. The limit of dynamical stability is reached when the left-hand side, and so the right-hand side, vanish:

β c I + + ρ χ ρ c I 0 − σ I − = 0 . $$ \begin{aligned} \beta _cI_++{\rho _\chi \over \rho _c}I_0-\sigma I_-=0 .\end{aligned} $$(15)

By their definitions, βc and σ are related by the central temperature and the chemical composition:

β c σ = k B T c μ m H c 2 · $$ \begin{aligned} \beta _c\sigma ={k_{\rm B} T_c\over \mu m_{\rm H} c^2}\cdot \end{aligned} $$(16)

We can use this relation to eliminate σ in (15):

β c 2 + ρ χ ρ c I 0 I + β c − k B T c μ m H c 2 I − I + = 0 . $$ \begin{aligned} \beta _c^2+{\rho _\chi \over \rho _c}{I_0\over I_+}\beta _c-{k_{\rm B} T_c\over \mu m_{\rm H} c^2}{I_-\over I_+}=0 .\end{aligned} $$(17)

For a given dimensionless structure (ξ, θ, ϕ, ψ, β/βc), a given central temperature and a given chemical composition, Equation (17) can be solved for βc as a function of the ratio ρχ/ρc:

β c = k B T c μ m H c 2 I − I + + ( ρ χ ρ c I 0 2 I + ) 2 − ρ χ ρ c I 0 2 I + · $$ \begin{aligned} \beta _c=\sqrt{{k_{\rm B} T_c\over \mu m_{\rm H} c^2}{I_-\over I_+}+\left({\rho _\chi \over \rho _c}{I_0\over 2 I_+}\right)^2}-{\rho _\chi \over \rho _c}{I_0\over 2 I_+}\cdot \end{aligned} $$(18)

Alternatively, it can be solved as a function of the density ρχ itself by eliminating ρc with the definition of βc:

β c = k B μ m H ρ c T c P c ≃ k B μ m H ρ c T c 1 3 a SB T c 4 ⟹ ρ c = μ m H k B a SB 3 T c 3 β c , $$ \begin{aligned} \beta _c&={{k_{\rm B}\over \mu m_{\rm H}}\rho _c T_c\over P_c}\simeq {{k_{\rm B}\over \mu m_{\rm H}}\rho _c T_c\over {1\over 3}a_{\rm SB} T_c^4} \quad \Longrightarrow \quad \rho _c={\mu m_{\rm H}\over k_{\rm B}}{a_{\rm SB}\over 3}T_c^3\beta _c ,\end{aligned} $$(19)

β c 2 = k B T c μ m H c 2 ( I − I + − ρ χ c 2 1 3 a SB T c 4 I 0 I + ) . $$ \begin{aligned} \beta _c^2&={k_{\rm B} T_c\over \mu m_{\rm H} c^2}\left({I_-\over I_+}-{\rho _\chi c^2\over {1\over 3}a_{\rm SB} T_c^4}{I_0\over I_+}\right) .\end{aligned} $$(20)

In this case, the equation for βc at the limit of stability does not necessarily have a real root. If

ρ χ c 2 1 3 a SB T c 4 > I − I 0 , $$ \begin{aligned} {\rho _\chi c^2\over {1\over 3}a_{\rm SB} T_c^4}>{I_-\over I_0} ,\end{aligned} $$(21)

the right-hand side of (20) is negative and so the condition for stability is always satisfied:

β c 2 > 0 > k B T c μ m H c 2 ( I − I + − ρ χ c 2 1 3 a SB T c 4 I 0 I + ) . $$ \begin{aligned} \beta _c^2>0>{k_{\rm B} T_c\over \mu m_{\rm H} c^2}\left({I_-\over I_+}-{\rho _\chi c^2\over {1\over 3}a_{\rm SB} T_c^4}{I_0\over I_+}\right) .\end{aligned} $$(22)

In other words, if there is enough dark matter to satisfy (21), the GR instability is completely removed for a given Tc and a given dimensionless structure (I0 and I−). This effect does not appear when we consider a fixed ratio ρχ/ρc because, since ρc decreases as the stellar mass increases, a fixed ratio ρχ/ρc corresponds to a decreasing value of ρχ, weakening the stabilising effect of dark matter, but as long as ρχ, Tc, I0, and I− are maintained constant, the instability can be reached only if the gas density decreases down to dark matter density for the destabilising post-Newtonian corrections to the dark matter gravitational field to become significant. Otherwise, the final mass of the SMS is set by fuel exhaustion instead of GR instability.

2.2. Hylotropes

The internal distribution of entropy (3) in rapidly accreting SMSs is well approximated by

β = { β c if M r < M core β c ( M r M core ) − 1 / 2 if M r > M core . $$ \begin{aligned} \beta =\left\{ \begin{array}{cc} \beta _c\qquad \qquad&\mathrm{if}\ M_r < M_{\rm core} \\ \beta _c\left({M_r\over M_{\rm core}}\right)^{-1/2}&\mathrm{if}\ M_r>M_{\rm core} \end{array}\right. .\end{aligned} $$(23)

The dimensionless ratio Mcore/M determines the relative distribution of entropy over the mass, and once it is fixed, all the dimensionless functions (8) are determined. These dimensionless structures are called hylotropes (Begelman 2010), and are thus uniquely classified by the dimensionless parameter Mcore/M. In particular, for each ratio Mcore/M, we know the values of all the dimensionless integrals in Equation (15). Once all the dimensionless functions are defined, there remain only two free parameters to determine the structure, plus one for dark matter. For the present purpose, it is convenient to choose the central temperature Tc. If we fix the last free parameter by imposing the critical condition (15), we obtain the properties of SMSs at the limit of stability, in particular the maximum masses consistent with stability:

M = 4 π ( K G ) 3 / 2 φ surf , $$ \begin{aligned} M&={4\over \sqrt{\pi }}\left({K\over G}\right)^{3/2}\varphi _{\rm surf} ,\end{aligned} $$(24)

M core = 4 π ( K G ) 3 / 2 φ core . $$ \begin{aligned} M_{\rm core}&={4\over \sqrt{\pi }}\left({K\over G}\right)^{3/2}\varphi _{\rm core} .\end{aligned} $$(25)

We note that the mass scale is fully determined by K, and for a mixture of ideal gas and radiation, this constant is fully determined by βc (and the chemical composition):

K = P c ρ c 4 / 3 = ( 3 a SB ) 1 / 3 ( k B μ m H ) 4 / 3 ( 1 − β c β c 4 ) 1 / 3 . $$ \begin{aligned} K={P_c\over \rho _c^{4/3}}=\left({3\over a_{\rm SB}}\right)^{1/3}\left({k_{\rm B}\over \mu m_{\rm H}}\right)^{4/3}\left({1-\beta _c\over \beta _c^4}\right)^{1/3} .\end{aligned} $$(26)

2.3. WIMPs capture

In the case of WIMPs capture, the dark matter component is distributed according to a thermal distribution (Taoso et al. 2008)

ρ χ = ρ χ , c e − r 2 r χ 2 r χ = 3 k B T c 2 π G ρ c m χ , $$ \begin{aligned} \rho _\chi =\rho _{\chi ,c}e^{-{r^2\over r_\chi ^2}} \qquad r_\chi =\sqrt{3k_{\rm B} T_c\over 2\pi G\rho _c m_\chi } ,\end{aligned} $$(27)

where mχ is the mass of the dark matter particles. The characteristic radius (27) can be expressed in terms of the length scale parameter α−1 (Equations 8 and 9):

r χ = ξ χ α ξ χ = 3 2 μ m H m χ β c $$ \begin{aligned}&r_\chi ={\xi _\chi \over \alpha } \qquad \xi _\chi =\sqrt{{3\over 2}{\mu m_{\rm H}\over m_\chi }\beta _c}\end{aligned} $$(28)

⟹ ρ χ = ρ χ , c e − ξ 2 ξ χ 2 . $$ \begin{aligned}&\Longrightarrow \qquad \rho _\chi =\rho _{\chi ,c}e^{-{\xi ^2\over \xi _\chi ^2}} .\end{aligned} $$(29)

We see that the dimensionless characteristic radius ξχ is proportional to the geometric mean of two ratios, βc = Pgas/P and the ratio of the average mass of the free particles of gas to the mass of the dark matter particles μmH/mχ. WIMPS models give typical values mχ ∼ 100 GeV, which is two orders of magnitude larger than the proton mass mH. Thus, for μ of the order of unity and βc of the order of one per cent, we have rχ ∼ 0.01α−1. The length scale α−1 corresponds to the ratio of the core radius to the dimensionless core radius ξcore. This last quantity is always in the range 1–7 for all the hylotropes, so that α−1 gives the order of magnitude of the core radius, and the characteristic radius (27) is always of the order of one per cent of the core radius.

3. Results

3.1. Homogeneous dark matter distribution

The density threshold above which dark matter completely removes the GR instability (Equation 21) is plotted in Figure 1 as a function of Mcore/M for different Tc, assuming homogeneous dark matter density. A change in Tc corresponds to a simple rescaling of the curve (i.e. a constant shift in logarithmic scales). For each Tc, the function grows monotonously, and for any given ρχ there is a ratio Mcore/M below which the GR instability is completely removed. Moreover, the fact that the function has a maximum, reached in the polytropic limit Mcore → M, implies that for each Tc there is a threshold in ρχ above which the GR instability is completely removed independently of Mcore/M. For the typical Tc of H-burning (∼108 K), the threshold is ∼10−4 g cm−3. More precisely, for Pop III SMSs fuelled by H-burning (Tc ∼ 2 × 108 K), the threshold is ∼3 × 10−3 g cm−3, while in the Pop I case (Tc = 8 − 9 × 107 K) it is ∼10−4 g cm−3. In both cases it corresponds to ∼10−3ρc. We note that, thanks to the thermostatic effect of H-burning, Tc remains nearly constant all along the H-burning phase, so that dark matter above this density threshold prevents the GR instability until fuel exhaustion. For the typical Tc of WIMP annihilation (∼106 − 107 K), the threshold is lower: ∼10−12 − 10−8 g cm−3.

thumbnail Fig. 1.

Dark matter density threshold above which the GR instability is completely removed for any stellar mass (Equation 21), as a function of the mass fraction of the convective core, for the indicated central temperatures and assuming homogeneous dark matter density.

The stability limits in the (Mcore, M) diagram are shown in Figure 2 for a homogeneous dark matter distribution, for μ = 0.6 and Tc = 1.8 × 108 K, typical values for Pop III SMSs in the beginning of the H-burning phase. For the dark matter parameter we considered both a constant ρχ/ρc, with values of log ρχ/ρc = −10, −9, …, −3 (orange lines), and a constant ρχ, with values ρχ = 0 and log ρχ [cgs] = −10, −9, …, −3 (red lines). The intersections of the curves correspond to the models where ρc = 1 g cm−3. We note that the lines of constant Mcore/M (grey lines) represent the asymptotes of the stability limits with constant ρχ (red curves). It reflects the fact that, as noted above, for each Tc and for each ρχ, there is a ratio Mcore/M below which the GR instability is completely removed (Figure 1).

thumbnail Fig. 2.

Limits of dynamical stability in the (Mcore, M) diagram for Pop III hylotropic SMSs (μ = 0.6, Tc = 1.8 × 108 K) in the presence of a homogeneous dark matter distribution with various densities ρχ. The red curves correspond to ρχ = 0 and to log ρχ [cgs] = −10, −9, …, −3 (from left to right); the orange curves to log ρχ/ρc = −10, −9, …, −3 (from left to right). The black, blue, and cyan lines are GENEC tracks for the indicated accretion rates (Haemmerlé et al. 2018a, 2019). The grey lines correspond to constant mass fractions of the convective core.

The limits are shown in Figure 3 for μ = 0.6 and Tc = 8.7 × 107 K, relevent for Pop I SMSs in the beginning of the H-burning phase. The orange lines correspond to the same constant values of the ratio log ρχ/ρc = −10, −9, …, −3 as in the Pop III case, and the red lines to constant values of ρχ = 0 and log ρχ [cgs] = −10, −9, … up to −5 only, because in the Pop I case higher densities satisfy condition (21), so that no limit can be shown (as seen in Figure 1). For a given stellar mass, the central density of SMSs is lower in the Pop I case than in the Pop III case because of an earlier start of H-burning (Haemmerlé et al. 2019). While in the Pop III case it is typically 1 g cm−3 near the instability, in the Pop I case it is ∼0.1 g cm−3, so that the red curve for log ρχ [cgs] = −n intersects the orange one for log ρχ/ρc = −n − 1. As a consequence, the intersection of the orange and red curves in Figure 3 corresponds to a central density of 0.1 g cm−3.

thumbnail Fig. 3.

Same as Figure 2, but for the Pop I case (μ = 0.6, Tc = 8.7 × 107 K). From left to right, the red curves correspond to ρχ = 0 and to log ρχ [cgs] = −10, −9, …, −5 only, since the GR instability is completely removed for log ρχ [cgs] ≥ −4.

The same limits are shown in Figure 4 for μ = 0.6 and Tc = 107 K, typical values for SMSs fuelled by WIMP annihilation (Freese et al. 2010). In this case the red lines correspond to constant values of ρχ = 0 and log ρχ [cgs] = −14, −9, … only up to −8 since for larger densities the GR instability is completely removed (Figure 1).

thumbnail Fig. 4.

Same as Figures 2 and 3, but for μ = 0.6 and Tc = 107 K, typical for the case of energetically significant WIMP annihilation. From left to right, the red curves correspond to ρχ = 0 and to log ρχ [cgs] = −14, −13, …, −8 only since the GR instability is completely removed for log ρχ [cgs] > −8.

By comparing Figures 2, 3, and 4, we see that a decrease in Tc translates into a shift of the stability limit towards higher masses. While for Tc ∼ 108 K the GR instability can be reached at M ∼ 105 M⊙ in the polytropic limit (Mcore → M), for Tc ∼ 107 K it requires masses M ≳ 2 × 106 M⊙. This effect reflects the fact that lower temperatures correspond to lower densities of the baryonic gas, and thus to smaller GR destabilising corrections. Moreover, because of the lower density of baryonic gas, the dark matter density required to modify the stability limit is lower when Tc is lower. For instance, for Mcore ∼ 10%M, while the limit for Pop III SMSs fuelled by H-burning is modified by dark matter only for ρχ ≳ 10−6 g cm−3 (Figure 2), the limit for SMSs fuelled by WIMP annihilation is modified as soon as ρχ ≳ 10−10 g cm−3 (Figure 4).

3.2. Centralised dark matter distribution

For the highly centralised distributions (27), we find that the mass-limit in the (Mcore, M)-diagram remains identical to the case without dark matter. These distributions are well approximated by a δ-distribution, which does not impact the stability of the star (as can be seen in Equations 4–6) since the enclosed mass remains identical in the case of contraction or expansion of a Lagrangian layer. The stability limit starts to be shifted only for ξχ ≳ 10, that is for mχ ≲ 10−4 GeV, orders of magnitude below the mass range of WIMPs models.

4. Discussion

4.1. Comparison with previous works

For polytropic SMS models, assuming homogeneous dark matter densities, McLaughlin & Fuller (1996) found that the stability limit starts to be significantly shifted towards higher masses as soon as ρχ ≳ 10−3ρc, which corresponds to ρχ ≳ 10−3 g cm−3 for Pop III SMSs and to ρχ ≳ 10−4 g cm−3 in the Pop I case. This threshold is visible Figures 2 and 3 in the polytropic limit Mcore → M. However, we see that when Mcore ≲ M/2, a smaller amount of dark matter is sufficient: for ρχ ∼ 10−4ρc the maximum mass is increased by a factor of a few as soon as Mcore ∼ 50%M, and by nearly an order of magnitude when Mcore ∼ 20%M; for ρχ ∼ 10−5ρc it is increased by about an order of magnitude if the core remains Mcore ∼ 10%M.

4.2. Final mass of SMSs in direct collapse

In the main channel of direct collapse, that is the collapse of a primordial atomically cooled halo without fragmentation into a central SMBH, the direct progenitor of the SMBH is a Pop III SMS accreting at rates 0.01–1 M⊙ yr−1 (e.g. Latif et al. 2013; Chon et al. 2018). In this case evolutionary models of SMSs fuelled by H-burning give Tc ≃ 2 × 108 K and Mcore ≳ 10%M (Haemmerlé et al. 2018a, 2019), so that a homogeneous dark matter distribution of 10−4 − 10−3 g cm−3 is required to increase the final mass by a factor of a few (Figure 2). The dark matter density must exceed 0.003 g cm−3 for the GR instability to be completely removed until fuel exhaustion (Figure 1). Since the H-burning time of SMSs is around 1 Myr (e.g. Umeda et al. 2016; Woods et al. 2017, 2020), we can estimate the maximum mass of SMSs to be ∼106 M⊙ in this case.

In the case of galaxy merger-driven direct collapse, the direct progenitor of the SMBH is a Pop I SMS accreting at rates potentially up to 100–1000 M⊙ yr−1 (e.g. Mayer et al. 2024), and this scenario requires a SMS mass ≳106 M⊙ at collapse (e.g. Montero et al. 2012). Figure 3 shows that masses in excess of 106 M⊙ are accessible in this case for a dark matter background ≳10−5 g cm−3 if accretion rates ∼1000 M⊙ yr−1 can be maintained on the star. For ∼10−6 g cm−3, the maximum mass can be increased by a factor of a few. The GR instability is completely removed during the H-burning phase only if the dark matter density is ≳10−4 g cm−3 (Figure 1), and because of the huge accretion rates accessible in galaxy mergers, we can expect masses up to 108 − 109 M⊙ to be accreted in the H-burning time.

For the cases where dark matter completely removes the GR instability in the approximation used here, the instability is reached only if the destabilising post-Newtonian corrections to the dark matter gravitational field become significant. It occurs once ρc ∼ ρχ, as ρc decreases for increasing stellar mass M. For a given Tc, the value of ρc scales with βc (Equation 19), which scales with M−1/2 (Equations 24–26). We see for ρχ ∼ 10−3 g cm−3 that the evolution from ρc ∼ 0.1 − 1 g cm−3 to ρc ∼ ρχ requires a decrease in ρc of two to three orders of magnitude, that is an increase in M of four to six orders of magnitude. Fuel exhaustion is expected to occur earlier.

However, the densities expected for the dark matter background at the centre of mini-halos are ≲10−10 g cm−3 (Freese et al. 2009). Figures 2 and 3 show that for such densities the stability limit is shifted only for Mcore ≲ 1%M for the Tc of H-burning. However, stellar models indicate that Mcore ≳ 5%M for the relevant masses (Haemmerlé et al. 2018a, 2019). We see that the stabilisation of a H-burning SMS by the gravitational field of a dark matter background requires unrealisticly high densities, and WIMP capture does not change the picture (Sect. 3.2). By comparison, rotation appears as a much more efficient stabilising agent, in agreement with Bisnovatyi-Kogan (1998). For SMSs accreting angular momentum at the ΩΓ-limit, hylotropic models indicate that in atomically cooled halos the final mass is increased by a factor of a few by the effect of rotation, while in galaxy mergers it is increased by orders of magnitude (Haemmerlé 2021a). With baryonic gas and rotation only, the final mass of SMSs is found to belong to distinct ranges: 105 M⊙ < M < 106 M⊙ for atomically cooled halos, and 106 M⊙ < M < 109 M⊙ for galaxy mergers.

On the other hand, in the case of WIMP annihilation, Tc ∼ 107 K are found for the relevant masses (Freese et al. 2010). In this case, a homogeneous dark matter background of ∼10−10 g cm−3 is sufficient to impact the stability limit via its gravitational field if Mcore ∼ 10%M (Figure 4). Moreover, independently of the effect of the dark matter gravitational field, the low temperatures imposed by the energetic effect of WIMP annihilation lead to a shift of the stability limit towards higher masses. As long as central temperatures ≲107 K are maintained, the GR instability is reached only for stellar masses ≳2 × 106 M⊙ (Figure 4). Thus, with WIMP annihilation, SMSs of M > 106 M⊙ can remain stable in atomically cooled halos and in galaxy mergers, even without any rotation. The detection of a SMS with such a high mass in an atomically cooled halo would thus be a sign of energetically significant WIMP annihilation in the core of the star.

5. Conclusion

In the present work we studied the impact of dark matter on the GR instability in SMSs via the effect of the dark matter gravitational field, as well as the effect of WIMP annihilation on the thermal state of the star. We considered hylotropic structures with different ratio of the convective, isentropic core’s mass Mcore to the total stellar mass M.

Via its gravitational field only, dark matter can in principle completely remove the GR instability in SMSs until fuel exhaustion (Figure 1), and can increase their final masses by orders of magnitude (Figures 2–4). The smaller the ratio Mcore/M is, the stronger the impact of dark matter on the stability limit is. However, for the expected densities of the dark matter background and for realistic stellar structures, the effect of the dark matter gravitational field remains negligible. The higher densities reached in the case of WIMPs capture do not change the picture because of the high centralisation of the captured particles (Sect. 3.2).

On the other hand, for the low central temperatures imposed by energetically significant WIMP annihilation, the stability limit is shifted by an order of magnitude towards higher masses, compared to the case of SMSs fuelled by H-burning. While for the central temperatures of H-burning the GR instability can be reached at M ∼ 105 M⊙, for the central temperatures given by WIMP annihilation it requires masses M ≳ 2 × 106 M⊙.

Thus, we conclude that in realistic conditions the gravitational field of dark matter does not impact the stability limit of SMSs, but WIMP annihilation can postpone the GR instability and increase the final mass by an order of magnitude. Overall, we can estimate that, with rotation and energetically significant WIMP annihilation, the final masses of SMSs formed in atomically cooled halos range in the interval 106 M⊙ < M < 107 M⊙. The detection of a SMS with mass > 106 M⊙ in an atomically cooled halo can be interpreted as evidence of energetically significant WIMP annihilation in the star’s core.

Acknowledgments

LH has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 833925, project STAREX).

References

  1. Andika, I. T., Jahnke, K., Onoue, M., et al. 2024, A&A, 685, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bañados, E., Venemans, B. P., Mazzucchelli, C., et al. 2018, Nature, 553, 473 [Google Scholar]
  3. Baumgarte, T. W., & Shapiro, S. L. 1999, ApJ, 526, 941 [NASA ADS] [CrossRef] [Google Scholar]
  4. Begelman, M. C. 2010, MNRAS, 402, 673 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bisnovatyi-Kogan, G. S. 1998, ApJ, 497, 559 [CrossRef] [Google Scholar]
  6. Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2024, Nat. Astron., 8, 126 [Google Scholar]
  7. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [Google Scholar]
  8. Chandrasekhar, S. 1964, ApJ, 140, 417 [Google Scholar]
  9. Chon, S., Hosokawa, T., & Yoshida, N. 2018, MNRAS, 475, 4104 [CrossRef] [Google Scholar]
  10. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  11. Ellis, S. A. R. 2022, JCAP, 2022, 025 [CrossRef] [Google Scholar]
  12. Feng, W.-X. 2023, Astronomy, 2, 22 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fowler, W. A. 1966, ApJ, 144, 180 [NASA ADS] [CrossRef] [Google Scholar]
  14. Freese, K., Gondolo, P., Sellwood, J. A., & Spolyar, D. 2009, ApJ, 693, 1563 [NASA ADS] [CrossRef] [Google Scholar]
  15. Freese, K., Ilie, C., Spolyar, D., Valluri, M., & Bodenheimer, P. 2010, ApJ, 716, 1397 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fuller, G. M., Woosley, S. E., & Weaver, T. A. 1986, ApJ, 307, 675 [Google Scholar]
  17. Haemmerlé, L. 2020, A&A, 644, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Haemmerlé, L. 2021a, A&A, 650, A204 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Haemmerlé, L. 2021b, A&A, 647, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018a, MNRAS, 474, 2757 [Google Scholar]
  21. Haemmerlé, L., Woods, T. E., Klessen, R. S., Heger, A., & Whalen, D. J. 2018b, ApJ, 853, L3 [Google Scholar]
  22. Haemmerlé, L., Meynet, G., Mayer, L., et al. 2019, A&A, 632, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Haemmerlé, L., Mayer, L., Klessen, R. S., et al. 2020, Space Sci. Rev., 216, 48 [Google Scholar]
  24. Haemmerlé, L., Klessen, R. S., Mayer, L., & Zwick, L. 2021, A&A, 652, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Haiman, Z., Rees, M. J., & Loeb, A. 1997, ApJ, 476, 458 [NASA ADS] [CrossRef] [Google Scholar]
  26. Herrington, N. P., Whalen, D. J., & Woods, T. E. 2023, MNRAS, 521, 463 [CrossRef] [Google Scholar]
  27. Hosokawa, T., Yorke, H. W., Inayoshi, K., Omukai, K., & Yoshida, N. 2013, ApJ, 778, 178 [Google Scholar]
  28. Kehrer, K. S., & Fuller, G. M. 2024, ArXiv e-prints [arXiv:2406.13887] [Google Scholar]
  29. Kouvaris, C., & Tinyakov, P. 2011, Phys. Rev. D, 83, 083512 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kovács, O. E., Bogdán, Á., Natarajan, P., et al. 2024, ApJ, 965, L21 [CrossRef] [Google Scholar]
  31. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. C. 2013, MNRAS, 436, 2989 [Google Scholar]
  32. Maiolino, R., Scholtz, J., & Curtis-Lake, E. 2023, A&A, submitted [Google Scholar]
  33. Maiolino, R., Scholtz, J., Witstok, J., et al. 2024, Nature, 627, 59 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mayer, L., Kazantzidis, S., Escala, A., & Callegari, S. 2010, Nature, 466, 1082 [Google Scholar]
  35. Mayer, L., Fiacconi, D., Bonoli, S., et al. 2015, ApJ, 810, 51 [Google Scholar]
  36. Mayer, L., Capelo, P. R., Zwick, L., & Di Matteo, T. 2024, ApJ, 961, 76 [NASA ADS] [CrossRef] [Google Scholar]
  37. McLaughlin, G. C., & Fuller, G. M. 1996, ApJ, 456, 71 [NASA ADS] [CrossRef] [Google Scholar]
  38. Montero, P. J., Janka, H.-T., & Müller, E. 2012, ApJ, 749, 37 [Google Scholar]
  39. Nagele, C., & Umeda, H. 2023, ApJ, 949, L16 [NASA ADS] [CrossRef] [Google Scholar]
  40. Nagele, C., Umeda, H., Takahashi, K., Yoshida, T., & Sumiyoshi, K. 2022, MNRAS, 517, 1584 [NASA ADS] [CrossRef] [Google Scholar]
  41. Nagele, C., Umeda, H., Takahashi, K., & Maeda, K. 2023a, MNRAS, 520, L72 [Google Scholar]
  42. Nagele, C., Umeda, H., & Takahashi, K. 2023b, MNRAS, 523, 1629 [NASA ADS] [CrossRef] [Google Scholar]
  43. Nandal, D., Regan, J. A., Woods, T. E., et al. 2023, A&A, 677, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rees, M. J. 1978, The Observatory, 98, 210 [NASA ADS] [Google Scholar]
  46. Regan, J. A., Visbal, E., Wise, J. H., et al. 2017, Nat. Astron., 1, 0075 [Google Scholar]
  47. Shibata, M., Uchida, H., & Sekiguchi, Y.-I. 2016, ApJ, 818, 157 [Google Scholar]
  48. Spolyar, D., Freese, K., & Gondolo, P. 2008, Phys. Rev. Lett., 100, 051101 [NASA ADS] [CrossRef] [Google Scholar]
  49. Taoso, M., Bertone, G., Meynet, G., & Ekström, S. 2008, Phys. Rev. D, 78, 123510 [CrossRef] [Google Scholar]
  50. Taoso, M., Iocco, F., Meynet, G., Bertone, G., & Eggenberger, P. 2010, Phys. Rev. D, 82, 083509 [CrossRef] [Google Scholar]
  51. Umeda, H., Hosokawa, T., Omukai, K., & Yoshida, N. 2016, ApJ, 830, L34 [Google Scholar]
  52. Wang, F., Yang, J., Fan, X., et al. 2021, ApJ, 907, L1 [Google Scholar]
  53. Woods, T. E., Heger, A., Whalen, D. J., Haemmerlé, L., & Klessen, R. S. 2017, ApJ, 842, L6 [Google Scholar]
  54. Woods, T. E., Agarwal, B., Bromm, V., et al. 2019, PASA, 36, e027 [Google Scholar]
  55. Woods, T. E., Heger, A., & Haemmerlé, L. 2020, MNRAS, 494, 2236 [Google Scholar]
  56. Woods, T. E., Patrick, S., Elford, J. S., Whalen, D. J., & Heger, A. 2021, ApJ, 915, 110 [NASA ADS] [CrossRef] [Google Scholar]
  57. Woods, T. E., Patrick, S., Whalen, D. J., & Heger, A. 2024, ApJ, 960, 59 [NASA ADS] [CrossRef] [Google Scholar]
  58. Wu, X.-B., Wang, F., Fan, X., et al. 2015, Nature, 518, 512 [Google Scholar]
  59. Yang, J., Wang, F., Fan, X., et al. 2020, ApJ, 897, L14 [Google Scholar]
  60. Zwick, L., Mayer, L., Haemmerlé, L., & Klessen, R. S. 2023, MNRAS, 518, 2076 [Google Scholar]

All Figures

thumbnail Fig. 1.

Dark matter density threshold above which the GR instability is completely removed for any stellar mass (Equation 21), as a function of the mass fraction of the convective core, for the indicated central temperatures and assuming homogeneous dark matter density.
In the text
thumbnail Fig. 2.

Limits of dynamical stability in the (Mcore, M) diagram for Pop III hylotropic SMSs (μ = 0.6, Tc = 1.8 × 108 K) in the presence of a homogeneous dark matter distribution with various densities ρχ. The red curves correspond to ρχ = 0 and to log ρχ [cgs] = −10, −9, …, −3 (from left to right); the orange curves to log ρχ/ρc = −10, −9, …, −3 (from left to right). The black, blue, and cyan lines are GENEC tracks for the indicated accretion rates (Haemmerlé et al. 2018a, 2019). The grey lines correspond to constant mass fractions of the convective core.
In the text
thumbnail Fig. 3.

Same as Figure 2, but for the Pop I case (μ = 0.6, Tc = 8.7 × 107 K). From left to right, the red curves correspond to ρχ = 0 and to log ρχ [cgs] = −10, −9, …, −5 only, since the GR instability is completely removed for log ρχ [cgs] ≥ −4.
In the text
thumbnail Fig. 4.

Same as Figures 2 and 3, but for μ = 0.6 and Tc = 107 K, typical for the case of energetically significant WIMP annihilation. From left to right, the red curves correspond to ρχ = 0 and to log ρχ [cgs] = −14, −13, …, −8 only since the GR instability is completely removed for log ρχ [cgs] > −8.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.