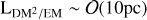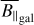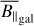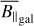© The Authors 2024

1 Introduction

The structure of the Milky Way is best expressed in terms of density, velocity, and force fields, as these can be related to the dynamical laws that govern the formation of structure and the overall shape of the Galaxy today. To our fortune, these fundamental quantities can be determined by a variety of observables that, to our misfortune, in general do not yield constraints for them individually, but are mixed and entangled in nontrivial and sometimes nonlinear ways.

Prominent examples of such observables combining several Galactic constituents are, for example, synchrotron radiation coupling the relativistic electron density, n_rel, with the perpendicular component of the Galactic magnetic field, B_⊥, or stellar polarization in both the optical and infrared regimes, which gives information on both the magnetic field direction and dust properties. The only route to disentangling these and similar observables and to mapping out the structure of the Galaxy is to cross-correlate them with each other and/or to compare them with simulations. For some observables, such a component separation has been successfully performed; for example, Planck Collaboration X (2016); Beyond Planck Collaboration (2023) separate the microwave sky into the cosmic microwave background (CMB) and astrophysical component maps or Selig et al. (2015); Scheel-Platz et al. (2023) separate the Fermi photon-count maps into point sources and diffuse emission of a hadronic and leptonic origin.

In this paper, we aim to disentangle the Galactic Faraday sky into its physical components. The Faraday effect entangles information on the line-of-sight (LoS) component of the magnetic field, B_‖, with the plasma electron density, n_e, into the Faraday depth, ϕ. It is the only observable that provides direct information on B_‖ for most regimes in the interstellar medium (ISM), apart from longitudinal Zeeman splitting, which may be observable in very dense regions such as molecular clouds (Beck & Wielebinski 2013), and circular polarization of synchrotron radiation, which will only be observable with next-generation radio telescopes (Enßlin et al. 2017). The Faraday effect has long been used to constrain the Galactic magnetic field strength (see e.g., Manchester 1972, 1974; Rand & Lyne 1994; Frick et al. 2001; Han et al. 2006; Sobey et al. 2019; Pandhi et al. 2022). Some of these works exploit the information of pulsars, which have the advantage of potentially providing Faraday data along with an independent measure on the column density of the interjacent electrons: the dispersion measure (DM). If one is interested in constraining large-scale Galactic models, pulsars come with the disadvantage that only a few with independent distance measurements are known (about 250 at the time of writing this paper), and hence one has to appeal to strong a priori assumptions about the magnetic field (Jaffe et al. 2010; Jansson & Farrar 2012) and/or the electron density (Cordes & Lazio 2002; Schnitzeler 2012; Greiner et al. 2016; Yao et al. 2017) of the Milky Way. Extragalactic Faraday data has also been used to constrain the Galactic magnetic field in conjunction with electron data stemming from free–free or H-α emission (Hutschenreuter & Enßlin 2020; Betti et al. 2019; Raycheva et al. 2022). In the first reference, henceforth abbreviated with HE20, the free–free sky was included as a phenomenological proxy for the Faraday depth amplitude. This permitted qualitative statements on the local structure of the Galactic magnetic field such as the alignment of the magnetic field with the local Orion spiral arm.

In this work, we replace the phenomenological model used in HE20 with a more physical one, with the aim of turning qualitative predictions into quantitative ones. In particular, we are interested in reconstructing the averaged LoS component of the magnetic field and the integrated electron density, also known as the DM for the full Galaxy. This is attempted with the help of four different datasets; namely, extragalactic Faraday data as compiled by Van Eck et al. (2023), pulsar data (Manchester et al. 2005), the free–free map of the Planck survey (Planck Collaboration X 2016), and an H-α map (Finkbeiner 2003).

The statistical methodology of this work rests on the same grounds as previous inferences of the Galactic Faraday depth sky in Oppermann et al. (2012), HE20 and Hutschenreuter et al. (2022); namely, information field theory (IFT). Information field theory is information theory for fields and field-like quantities and can cope with large, incomplete, and noisy datasets (for references to IFT, see Enßlin (2019), and for the accompanying python package¹ NIFTy in which the algorithm used in this work is implemented, see The NIFTy5 team et al. (2019)).

We structure the paper as follows. Sect. 2 describes the physical observables relevant for this paper, putting special emphasis on effects that correlate the different relevant physical quantities. Section 3 then explains the different models the data is interpreted in. Section 4 discusses the results and finally Sect. 5 gives a conclusive summary.

2 Observables

In order to simplify notation in the following, we introduced the LoS-average over a quantity, x: $${\langle x\rangle }_{{\text{L}}_{\text{i}}}\equiv \frac{1}{{\text{L}}_{\text{i}}}{\displaystyle {\int }_0^{{\text{L}}_{\text{i}}}dlx,}$$(1)

with L_i indicating the length of the LoS i. In a slight abuse of notation, we used L for both the identification and the length of the LoS. In this spirit, the subscript, i, can be used to identify either a specific LoS or subclasses of LoS. For example, we used L_gal to refer to all LoSs that trace the full Galaxy, where the boundary is implicitly defined via the physical processes that generate the data. We assume that all the processes used in this work trace the same LoSs, if not explicitly modeled otherwise. We also would like to note that the electron density referred to in this work mostly describes the thermal component, although strictly speaking the rotation measure (RM), DM, and free–free emission measure (EM) measurements are also slightly sensitive to the relativistic electrons, which, however, make only a very small contribution to all three tracers. In theory, suprathermal free electrons could also contribute to the electron population.

However, as there is very little evidence of pervasive supratherma electron populations in the ISM (Gurnett et al. 2021), we do not explicitly include this component in the current analysis.

2.1 Pulsar dispersion measures

2.1.1 Physics

Pulsars are magnetized and rapidly rotating neutron stars (Lorimer & Kramer 2004) emitting beamed electromagnetic radiation. This results in periodic radio pulses. As light travels slower within interstellar plasma at lower frequencies, the arrival time, t, of the pulse varies with the frequency, v, which can be expressed as (Draine 2011) $$\frac{\partial \text{t}}{\partial v}=-\frac{e^2}{\pi v^3{m}_{e}c}{\text{DM}}_{\text{P}}.$$(2)

The physical constants, e, m_e, and c, describe the elementary charge, the electron mass, and the speed of light, respectively. We introduced the DM as the integral over the electron density, n_e, $${\text{DM}}_{\text{P}}={\text{L}}_{\text{p}}{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{p}}}.$$(3)

The LoS L_P goes from the pulsar, P, to Earth. Therefore, DMs obtained from pulsars provide a lower limit on the Galactic DM sky for the respective LoSs they probe and, due to the fact that the DM monotonically increases along the LoS, can serve as a distance proxy. This can be expressed in several ways; for example, on the DM level by defining the residual DM “behind” the pulsar as $${\text{DM}}_{\text{res}}={\text{DM}}_{\text{gal}}-{\text{DM}}_{\text{P}},$$(4)

where L_Gal ≥ L_P and DM_res ≥ 0. Some pulsars have distance measurements independent of n_e, mostly determined via parallaxes, association with known structures, or HI absorption. The pulsar distances, L_P, can be related to the DM_P models via $${\text{L}}_{\text{P}}=f\left({\text{DM}}_{\text{P}}\right).$$(5)

Here, f is a monotonically increasing function that encodes the electron distribution along the given LoS, and is hence different for each position on the sky.

2.1.2 Data

We used the Australia Telescope National Facility (ATNF) (Manchester et al. 2005) catalog of pulsars². The DM errorbars given in the catalog are determined by propagating the arrival time uncertainties by taking Eq. (2) at face value. As the arrival timing is very precise, this leads to signal-to-noise ratios (S/Ns) in the DM of up to 10⁸. Several systematic effects may slightly limit the interpretation of Eq. (2) as a direct measure of the electron column density (Kulkarni 2020). We hence adapted a maximum S/N of 0.001 for the DM data; that is, sources with a higher S/N got their error bars adapted accordingly. The catalog also provides distance measurements, mostly from parallaxes, associations with known objects (e.g., globular clusters), or HI absorption. If an object has several independent distance measurements available, we included all measurements in our analysis. In some cases, distances provided in the catalog are processed data (e.g., Verbiest et al. (2012)) that combine several distance measures. In these cases, we only considered the processed data and disregarded data points that had been used in the processing. In general, we only considered measurements with well-defined error bars. In total, the catalog includes 264 independent distance measurements usable in this work, 130 of which are parallaxes. We show a projection of all pulsar DMs used in this work in Fig. 1a.

Fig. 1 Sky projections of all datasets used in this work. These are pulsar DMs from the ATNF catalog (panel a; Manchester et al. 2005), RMs stemming from the van Eck catalog (panel b; Van Eck et al. 2023) and the EMs calculated from free–free (panel c; Planck Collaboration X 2016) and H-α (panel d; Finkbeiner 2003) emission. The latter two datasets are shown on a logarithmic scale. We show the quality masks employed for the EM data (see the discussion in Sect. 2.3.2) in panels (e) and (f), with 0 indicating a masked pixel. These and all of the following sky maps are presented in Galactic coordinates centered at (l, b) = (0°, 0°), with longitude increasing to the left.

2.2 Faraday rotation measures

2.2.1 Physics

The differential angle of rotation, Δ_λ, of the polarization plane of linearly polarized light traveling through a magneto-ionic plasma, can be described by the following formula (Burn 1966): $${\text{Δ}}_{\lambda }=\text{RM\hspace{0.17em}}{\lambda }^2,$$(6)

where λ is the observational wavelength and RM is the rotation measure, defined by this equation. Determining RMs is usually done by observing Δ_λ at different wavelengths and fitting the result in the λ² space. In the ideal case of a thin plasma screen being the only source for the rotation effect, the RM is equal to the Faraday depth, ϕ, which is defined via $$\begin{array}{c}\varphi =\frac{e^3}{2\pi m_e^2{c}^4}{\displaystyle {\int }_{\text{LoS}}dl{n}_{\text{e}}{B}_{\Vert }}\\ =0.812{\displaystyle {\int }_{\text{\hspace{0.17em}LoS}}dl[\text{pc}]n_{\text{e}}\left[\text{c}{\text{m}}^{-3}\right]B_{\Vert }[\text{μG}],}\end{array}$$(7)

where B_‖ is the LoS-parallel component of the magnetic field. We can use Eq. (7) to define an n_e-weighted average of B_‖ in the Milky Way, 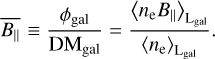$$\overline{B_{\Vert }}\equiv \frac{{\varphi }_{\text{gal }}}{{\text{DM}}_{\text{gal }}}=\frac{{\langle n_{\text{e}}{B}_{\Vert }\rangle }_{{\text{L}}_{\text{gal }}}}{{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}}.$$(8)

This gives a direct and simple connection to extract information on the magnetic field from the ϕ_gal and DM_gal skies. We note that in the case of By and n_e being statistically independent, 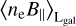${\langle n_{\text{e}}{B}_{\Vert }\rangle }_{{\text{L}}_{\text{gal }}}$ Simplifies to ${\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}{\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$, which implies that ${\overline{B_{\Vert }}}_{\text{gal }}={\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$; in other words, we can extract the unbiased average of the LoS parallel component of the magnetic field from ϕ_gal.

Since this is a very important case for the interpretation of ${\overline{B_{\Vert }}}_{\text{gal }}$, we investigated the correlation between B_‖ and n_e in more detail. We started with the relationship between the absolute value of the full magnetic field vector, |B|, and n_e, which is physically more tangible. From a theoretical perspective, both correlation (due to compression in shock fronts (Roberts 1969) or in gravitationally collapsing structures) and anticorrelation (due to magnetic pressure compensating for the lack of gas pressure in conditions close to pressure equilibrium (Beck et al. 2003)) are fathomable. Observationally, the two quantities are generally decoupled in the warm ISM (Crutcher et al. 2010), but may be correlated in denser regions such as molecular clouds (Harvey-Smith et al. 2011; Purcell et al. 2015) that may dominate the average for certain LoSs (see also discussion in HE20). Simulations have shown that for typical ISM conditions both quantities are uncorrelated on kiloparsec scales in the subsonic regime (Seta & Federrath 2021).

However, from a purely mathematical standpoint, the statistical independence of |B| and n_e does not of course imply the same for B_‖ and n_e. Since our position in the Milky Way is in no way special, only geometric effects and/or an alignment of the magnetic field with Galactic structure should introduce such correlations, which makes the scenario of a strong all-sky correlation between the two quantities (in the case ${\langle |B|n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal }}}=0$ holds) unlikely. But locally some correlation is expected and indeed, Faraday rotation and Planck dust polarization data have indicated that B_‖ might be correlated with specific Galactic structures such as the Local Arm (HE20). Furthermore, the THOR survey (Shanahan et al. 2019) has found evidence for a correlation of a strong Faraday excess and the Sagittarius Galactic arm, and such a correlation between Galactic arms and Faraday excesses is expected by simulations (Reissl et al. 2020). All of these are correlations of projected quantities that in principle do not yet imply correlation along the LoS, but we do regard it as plausible in these cases.

To summarize, there is a solid body of evidence that the assumption of statistical independence between B_‖ and n_e holds for a wide range of scales in the Milky Way and on the sky, but also the indication that it might break down for specific structures on the sky. Equation (8) has been used throughout the literature to estimate the average magnetic field strength, mostly for specific pulsars (Manchester 1972, 1974; Han 2009). It should be noted that the LoS-averaged magnetic field strength, 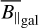${\overline{B_{\Vert }}}_{\text{gal }}$, can significantly underestimate the typical magnetic field strength if field reversals occur; that is, in strongly turbulent environments.

2.2.2 Data

In this work, we rely on the same pre-compiled data catalog of extragalactic RMs (Van Eck et al. 2023) as in Hutschenreuter et al. (2022), including the same preprocessing routines. We furthermore have used the error estimate provided by Hutschenreuter et al. (2022) instead of the observational errors, as in those the potential extragalactic components and observational systematic effects from, for example, nπ-ambiguities (Ma et al. 2019) are already factored in. A projection of the dataset is shown in Fig. 1b. We do not include RMs of pulsars in the inference model, as the small number of pulsars with associated RMs does not warrant the more complex modeling required for the residual Faraday depth behind the pulsars³. We do, however, utilize these RMs to validate our model in Sect. 4.4.

2.3 The electron emission measure

2.3.1 Physics

A further tracer of the electron column density is the Galactic emission measure, defined via $${\text{EM}}_{\text{gal}}={\text{L}}_{\text{gal}}{\langle n_{\text{e}}^2\rangle }_{{\text{L}}_{\text{gal}}}.$$(9)

As we are interested in the connection to the Galactic DM sky, it is worth noting that one can interpret n_e as a statistical process along the LoS. One can then write for the variance 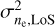${\sigma }_{n_{\text{e}}\text{,LoS}}^2$ of this process along a Galactic LoS: 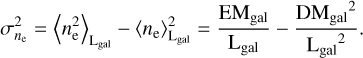$${\sigma }_{n_{\text{e}}}^2={\langle n_{\text{e}}^2\rangle }_{{\text{L}}_{\text{gal}}}-{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}^2=\frac{{\text{EM}}_{\text{gal}}}{{\text{L}}_{\text{gal}}}-\frac{{\text{DM}}_{\text{gal}}{}^2}{{\text{L}}_{\text{gal}}{}^2}.$$(10)

There are several possible ways to connect the EM_gal and DM_gal skies. Of these, models that are easily interpretable and for which a priori constraints can be formulated are preferable. Motivated by simple dimensional analysis to cancel the density units, we then calculate 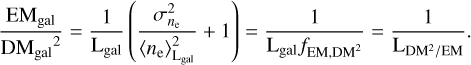$$\frac{{\text{EM}}_{\text{gal}}}{{\text{DM}}_{\text{gal}}{}^2}=\frac{1}{{\text{L}}_{\text{gal}}}\left(\frac{{\sigma }_{n_{\text{e}}}^2}{{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}^2}+1\right)=\frac{1}{{\text{L}}_{\text{gal}}{f}_{{\text{EM}}^2{\text{,DM}}^2}}=\frac{1}{{\text{L}}_{D{M}^2/EM}}.$$(11)

Here, we introduced the unitless conversion factor, f_EM,DM, which is strictly positive and smaller than one, and the EM–DM path length, 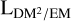${\text{L}}_{{\text{DM}}^2\text{/EM}}$. We shall construct a model for the ${\text{L}}_{{\text{DM}}^2\text{/EM}}$ sky in Sect. 4.1.3, which allows us to connect the EM and DM datasets.

In order to be able to construct a prior on the 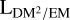${\text{L}}_{{\text{DM}}^2\text{/EM}}$ sky and to interpret the results of the inference, we discuss the possible limits and interpretations of Eq. (11). The f_EM,DM factor approaches one if n_e is close to constant $\left({\sigma }_{n_{\text{e}}}\ll {\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}\right)$ and zero if n_e has strong variability along the LoS (i.e., ${\sigma }_{n_{\text{e}}}\gg {\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}$). 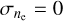The simplest conceivable case is hence that of a constant density along the LoS, implying ${\sigma }_{n_{\text{e}}}=0$, and therefore L_galEM_gal = DM_gal²; that is, the EM–DM² ratio simply gives the inverse length of the LoS. 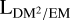${\text{L}}_{{\text{DM}}^2\text{/EM}}$ thus provides a lower limit on the length of the LoS. A slightly more complicated model already often used in the literature (i.e., Pynzar’ 1993; Berkhuijsen & Müller 2008; Harvey-Smith et al. 2011) assumes the ionized ISM to be composed of internally uniform clouds with little to no ionized matter in between. In this particular case, f_EM,DM can be viewed as the fraction of the LoS that is ionized, and is equal to the LoS filling factor, f. Allowing for internal density fluctuations in these clouds and cloud-to-cloud variations leads to the ionized-cloudlet model (Cordes et al. 1991; Cordes & Lazio 2002; Ocker et al. 2020), in which case f_EM,DM can be parameterized in terms of these variations and the overall filling factor, f. In the general case, 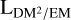${\text{L}}_{{\text{DM}}^2\text{/EM}}$ approximates the size of the part of an LoS that exhibits the largest n_e values.

Since 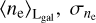${\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}},{\sigma }_{n_{\text{e}}}$, and L_gal can vary strongly and do not depend on each other, the interpretation of the ${\text{L}}_{{\text{DM}}^2\text{/EM}}$ calculated from EM and DM measurements must rely on additional assumptions. We illustrate this point by presenting two examples of possible n_e configurations along a LoS in Fig. 2, which give very similar observational results, albeit depicting completely different scenarios for the n_e distribution. 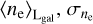It should further be noted that ${\text{L}}_{{\text{DM}}^2\text{/EM}}$ can be directly calculated from EM and DM values, while ${\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}},{\sigma }_{n_{\text{e}}}$ and L_gal are 3D-model dependent quantities; in particular, all three depend on the definition of the border region of the Milky Way. All our sky models are independent of this choice, but their interpretation with regard to the 3D structure of the Galaxy is not. We give a simple example of such a 3D model in Sect. 4.1.3, as it is more connected to the concrete interpretation of our results.

At this point, we would also like to note that the dimensional analysis argument used to motivate Eq. (11) could also be used to cancel the units of length instead of the density units; in other words, to calculate 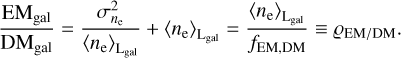$$\frac{{\text{EM}}_{\text{gal}}}{{\text{DM}}_{\text{gal}}}=\frac{{\sigma }_{n_{\text{e}}}^2}{{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}}+{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}=\frac{{\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}}{f_{\text{EM},\text{DM}}}\equiv {\varrho }_{\text{EM}/\text{DM}}.$$(12)

This equation is not as useful as Eq. (11) for our sky model, as we found it more difficult to put physical a priori assumptions on this fraction. Nonetheless, the quantity ϱ_EM/DM is still interesting for the interpretation of our results, especially in the limit 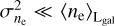${\sigma }_{n_e}^2\ll {\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}$, in which it is simply equal to the average electron density along the LoS. In general, due to the limits of ϱ_EM,DM, ϱ_EM/DM provides an upper limit for 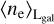${\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{gal}}}$, and can be interpreted as the LoS-averaged electron density weighted by itself.

Fig. 2 Illustration of the EM-DM relation for two simple models, discussed in Sect. 2.3.1. The red graph shows a short LoS with relatively weak variations in ne, while the blue one shows a long LoS with strong variations. Albeit depicting two completely different environments, the calculated DM, EM, and ${\text{L}}_{{\text{DM}}^2\text{/EM}}$ values for an observer sitting at L = 0 approximately agree. The units in this illustration are arbitrary, as the effect is scale-invariant. Its main intention is to demonstrate the interpretational limitations of Eq. (11). A more physical illustration of the Milky Way is provided later in Sect. 4.1.3.

2.3.2 Data

There are several tracers that give information on EM_gal. In this work, we use the EM map provided by the Planck mission, derived from microwave free–free emission (the bremsstrahlung resulting from the interaction of free protons and electrons), and an H-α emission map compiled by Finkbeiner (2003) based on several surveys (Dennison et al. 1998; Gaustad et al. 2001; Haffner et al. 2003) tracing the optical hydrogen Balmer-α line. Both effects are not clean tracers of EM_gal, but require a careful consideration of systematic biases. In this work, we utilize data from both sources, but seek to minimize possible biases by either correcting for them or, if this is not possible, masking the respective sky areas where the datasets become unreliable.

Free–free emission measure. Free-free emission is an important Galactic foreground in the microwave sky, especially in the regime around 30 GHz, and was therefore accurately determined by CMB missions such as Planck (Planck Collaboration X 2016) or WMAP (Bennett et al. 2013). The observed free–free emission depends on two Galactic environmental variables; namely, the (squared) electron density, n_e, and the electron temperature, T_e. The Planck team has produced both T_e and EM maps (Planck Collaboration X 2016) via an elaborate component separation technique (Eriksen et al. 2008). At high latitudes, the Planck EM map contains many bright point-like objects that correspond to extragalactic objects (Planck Collaboration X 2016). Since this is only partially reflected in the statistical uncertainties, these sources contaminate the dataset, especially at high latitudes. The Planck has provided a mask of point sources for all frequency channels. We have used the 30 GHz mask to mask all point sources with |l| > deg 10. At lower latitudes, the Planck mask also excludes structures clearly belonging to the disk. Additionally, we have hence decided to mask all points in the Planck EM dataset with an S/N < 10, which effectively removes most remaining point sources. We note that this S/N cut results in a rather conservative mask, as this discards many more areas of the sky than just the point sources and effectively only leaves the disk and some very bright regions of the sky (about 12.3% of the full sky remains). We are ready to accept this downside, as H-α emission provides a good complementary dataset.

2.3.3 H-α EM

With knowledge of the electron temperature, the H-α intensity, I_H−α, can be related to the EM via 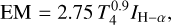$$\text{EM}=2.75T_4^{0.9}{I}_{\text{H}-\alpha },$$(13)

with T₄ being the temperature in units of 10000 K and I_H-α being measured in Rayleigh (Haffner et al. 1998). We used the Planck temperature map for the T₄ factor, noting that for many parts of the sky this map is basically unconstrained and shows the 7000K prior adopted by Planck. While Eq. (13) is a very well-established relation, light stemming from H-α emission is obscured by dust, which limits its use as a tracer of the full EM_gal, especially in the inner parts of the Galaxy. Dickinson et al. (2003) have developed a method to correct for this effect by utilizing the dust extinction (E – B)_V map provided by Schlegel et al. (1998). In that, they calculate the optical depth, τ, for H-α via 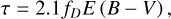$$\tau =2.1f_{D}E(B-V),$$(14)

where E (B – V) is the extinction between the B and V bands in magnitude, and the 2.1 factor encompasses the conversion from magnitudes to the natural logarithm and a correction factor for converting B – V to H-α extinctions (Finkbeiner 2003). The factor, f_D, is an additional fudge factor that encodes the proportion of dust being in front of behind H-α emitting regions, with 0 indicating no absorption and 1 full dust absorption (i.e., all dust is in front of the emitting gas). In principle, this factor most likely has a strong all-sky dependence, but Dickinson et al. (2003) have determined f_D = 0.33 ± 0.1 to be a good approximation for most of the sky. We adopted this value, but note that this a simplification and may bias our results locally (see also Sect. 3.3). We further masked all sky pixels with t > 1, in accordance with Dickinson et al. (2003); Berkhuijsen & Müller (2008), which disregards most of the inner Galactic disk. This leaves about 96% of the EM sky constrained by H-α data.

In summary, about 8.9% of the sky is constrained by both H-α and free-free data and 0.15% is covered by none of the datasets. In the former regions, we note a Pearson correlation coefficient of ˜0.7 between both EM datasets. We calculated an error-weighted average of the difference between the two datasets, $\left(d_{\text{E}{\text{M}}_{\text{H}\alpha }}-d_{\text{E}{\text{M}}_{\text{ff}}}\right)/\left(\sqrt{{\sigma }_{EM}^2{}_{\text{H}\alpha }+{\sigma }_{E{M}_{ff}}^2}\right)$, of about –1.7, with a scatter of about 9.5. While this demonstrates an acceptable correspondence, we note that several pixels show discrepancies over an order of magnitude or more, indicating that some residual biases are still present in the datasets. We show both the free-free and H- EMs that we used as inputs for our model in Fig. 1, as well as the respective masks.

3 The models

In the following, we use Eqs. (3), (7), (9) to construct a joint inference model connecting all of the observables discussed in Sect. 2 via full sky maps. We refer to the Faraday rotation, DM, EM sky maps as observables, as they are directly related to the datasets. We developed a model for each sky map, which we annotate with s_x (l, b), where 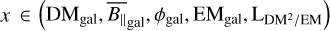$x\in \left(D{M}_{\text{gal }},{\overline{B}}_{\Vert \text{gal }},{\varphi }_{\text{gal }},E{M}_{\text{gal }},{\text{L}}_{D{M}^2/EM}\right)$. This notation is used to clearly distinguish between the datasets (annotated similarly with d_x) and our sky models. We constrained ourselves to models in which all components have a physical interpretation, with potential degeneracies minimized as far as possible. The fundamental building blocks of these sky models are Gaussian fields (indicated with Greek letters), each of which has an a priori independent unknown homogenous correlation structure that is inferred simultaneously. These correlation structures are each dependent on a set of hyperparameters, which encode our a priori expectations on the structure; for example, their expected correlation lengths or the expected range of fluctuations. These parameters are usually set conservatively and will allow for a somewhat larger range of possible field realizations than what is physically plausible. A more detailed discussion on the correlation model can be found in Arras et al. (2022). We discuss and illustrate the prior of each sky map in Appendix A.

The sky models for the observables, O ∈ (DM_gal, ϕ_gal, EM_gal), are connected to the datasets via 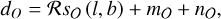$$d_O=ℛs_O(l,b)+m_O+n_O,$$(15)

where R is a response operator projecting the sky model to data space, n_O is the random observational noise term, and m_O contains systematic data biases that are modeled explicitly as far as possible.

3.1 Galactic sky models

We began with the development of the sky model, SDM_gal (l, b), as the DM_gal sky is a component that affects all of the other observable sky quantities considered here. We note that it is a strictly positive quantity, with expected all-sky variations in the Galactic DM over several orders of magnitude. Such a pattern can be naturally modeled via a log-normal model; that is, we set $$s_{D{M}_{gal}}(l,b)=e^{\rho }.$$(16)

and assumed ρ to be a field with homogeneous and isotropic Gaussian statistics. We adjusted the hyperparameters of ρ such that the value range of 1 pc cm^–3 to 10 000 pc cm^–3 is conveniently covered (see Appendix A).

We could then use Eq. (8) to write the sky model for the Galactic Faraday sky as 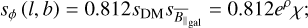$$s_{\varphi }(l,b)=0.812s_{DM}{s}_{\overline{B_{lgal}}}=0.812e^{\rho }\chi ;$$(17)

that is, the model for the magnetic field sky, χ obeys Gaussian prior statistics. Here, the hyperparameters on χ were set to easily encompass the typical amplitude of the magnetic field in the Milky Way (i.e., on the order of a few µG. We again illustrate the prior in Appendix A). This model is analogous to the model introduced in HE20 and Hutschenreuter et al. (2022), with the difference being that the degeneracy between the amplitude field, e^ρ, and sign-determining field, χ, is now broken by the DM data, which constrains Eq. (16).

The last observable to connect is the Galactic EM. Observing Eq. (11), we propose the following model: 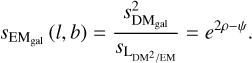$$s_{E{M}_{gal}}(l,b)=\frac{s_{D{M}_{gal}}^2}{s_{{\text{L}}_{D{M}^2/EM}}}=e^{2\rho -\psi }.$$(18)

The newly introduced model, 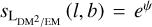$s_{{\text{L}}_{{\text{DM}}^2/\text{EM}}}(l,b)=e^{\psi }$, captures the 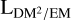${\text{L}}_{{\text{DM}}^2/\text{EM}}$ factor used to translate the EM and DM skies. We again chose a log-normal model, as this factor is strictly positive and most likely varies over orders of magnitude. The 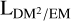${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky is expected to vary between the order of 1 pc and several 10⁵ pc (i.e., the size of the Milky Way) a priori. We discuss and illustrate the prior on ψ in more detail in Appendix A.

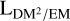There are good physical reasons to believe that the true logarithmic, $\text{DM,}{\overline{B_{\Vert }}}_{\text{gal }}$, and logarithmic, ${\text{L}}_{{\text{DM}}^2/\text{EM}}$, maps (which are the sky maps with Gaussian priors in our model) also contain structures that are a priori unlikely in our model, such as filaments that are seen in Galactic HI (Clark et al. 2014) or dust maps (Planck Collaboration Int. XXXII 2016). We emphasize that the assumption of statistically homogenous and isotropic Gaussian fields only constitutes an a priori constraint, and the posterior maps may contain such structures if driven by the data. To our knowledge, there exists no physically informed, efficient, and unbiased model for the correlation structure of the full sky, which we could use to improve our prior.

Fig. 3 Graph illustrating the hierarchical Bayesian model employed in this work. The sky models in the upper layer correspond to the Gaussian fields, ψ,ρ, and χ, in that order. This graph omits several layers at the top, which are similar for each Gaussian field and contain the correlation structure modeling. For details on those, see Appendix A and Arras et al. (2022).

3.2 Data space models

The integrals in Eqs. (3), (7), and (9) will typically receive their most significant contributions from the Milky Way for most LoSs and the observables in question. Nonetheless, all three datasets are subject to systematic effects, which are in part caused by additional or neglected physical contributions, but also by systematic effects in the data processing. In the case of Faraday RM and free-free EM data, we used the updated error bars inferred by HE20 and Hutschenreuter et al. (2022), which implicitly correct for such effects. For the pulsar DM and distance datasets used in our work, we developed new models, which are detailed below.

3.2.1 Pulsar dispesion measure

As is discussed in Sect. 2, observational errors of pulsar DMs are generally small and well understood. The biggest systematic effect of DM_P as a tracer of DM_gal comes from the fact that most pulsars lie within the Milky Way; that is, we trace only a limited part of the respective L_gal. In order to model this effect, we introduced an explicit model for the pulsar DM. This is necessary, as we have no good statistical measure to estimate the Galactic contribution similarly as for the extragalactic Faraday data, which relied on all-sky correlations.

A very simple model for the pulsar DM can be constructed by introducing a factor, w_P, for each pulsar, 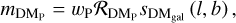$$m_{D{M}_{\text{p}}}=w_{\text{p}}{ℛ}_{D{M}_{\text{p}}}{s}_{D{M}_{gal}}(l,b),$$(19)

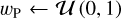where $w_{\text{P}}\leftarrow \mathcal{U}(0,1)$; that is, assuming a uniform prior on the relative position of the pulsar along the LoS, if measured in DM units. This model does not make any a priori assumptions about the geometry of the Milky Way, which implies that we put equal likelihood on a pulsar tracing any percentage of the LoS, irrespective of its angular position on the sky. This model has the advantage of being almost entirely data-driven, which is to say it does not require an explicit three-dimensional (3D) model of the Milky Way. One should note at this point that an implicit assumption of Eq. (19) is that the pulsars are tracing a significant portion of the LoS, as the uniform weighting disfavors a DMP orders of magnitudes smaller than the respective DM_gal on the sky. Nonetheless, this model still leaves room for some degeneracy, as it might still be possible to consistently decrease w_P for the pulsars and increase the DM_gal and still explain the data with the same explanatory power. Hence, if constrained with pulsar data alone, the model can only provide a lower limit on DM_gal and offset inconsistencies when explaining pulsars with different DMs along the same LoS. We furthermore do not cover any selection effects; if certain parts of the Milky Way are not sampled by pulsars, this will lead to systematic effects in our results. We note that a viable alternative might be to use an existing 3D electron model to construct this prior, but this would lead to the problem of quantifying the uncertainty on the DM predicted by these models. In the specific case of the most recent Yao et al. (2017) electron model (henceforth abbreviated as YMW), Ocker et al. (2021) have indicated that the model uncertainties are not widely understood, and we have hence opted for our simpler uniform model. Constructing a better-informed prior on the relative pulsar DM and distances would increase the accuracy of our result, but is left to future work.

3.2.2 Pulsar distances

Due to the relative scarcity of pulsars, we additionally have used independently measured distance data that is available for some pulsars (see Sect. 2.1.2) to introduce an additional likelihood term. To this end, we built a model for the path length, L_P, by translating the predicted DMs for each pulsar to distances by translating Eq. (5) into a model equation: 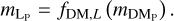$$m_{Lp}=f_{DM,L}\left(m_{DMP}\right).$$(20)

In this work, we have used the YMW model to construct the conversion function, f_DM,L. The desired effect of this additional likelihood term is additional constraints on the large-scale structure on the sky. Given the small number of pulsars with independent distance measurements and the typically large error bars of these distances, we do not expect a strong impact for smaller structures. We have tested the impact of this additional term by running inferences with and without the additional distance data. We find that including the pulsar distances significantly stabilizes our results, and we hence accept the small downside of including a weak dependence on an explicit electron density model into our inference, especially as the same model is also implicitly present in the error bars of the Faraday dataset (see Sect. 2.2.2). We refrained from putting additionally a priori constraints on our model. Any systematic effects resulting from this are discussed in the next section.

3.3 Model summary and evaluation

The full model is summarized and illustrated in Fig. 3. This figure shows that our model consists of three branches stemming from the three datasets. We hence refer to these as the RM, DM, and EM branches for the rest of the paper. The construction of the model as well as the interpretation of the results is conditional on several assumptions and unresolved systematic effects, which we summarize below:

• Insufficient volume sampling of n_e via pulsars: The volume density of observed pulsars in the Milky Way is unfortunately still very low and far from uniform. Specifically, the inner Galactic disk (l ≈ 0) has most likely not been sampled at all beyond a certain distance. If we take the YMW model as a reference, almost all of the pulsars lie in the nearest half of the Milky Way. We hence expect our Galactic disk results to underestimate the true DM_gal by at least a factor of two. Following from this, our magnetic field estimates in the disk are most likely overestimated by the same factor, as the extragalactic RM data probes the full disk. We have refrained from fixing this via, for example, a volume prior on the Milky Way, as this would only obfuscate the issue, while bringing little to no new insights. Future pulsar surveys are projected to have a very deep luminosity limit in the Milky Way (van Leeuwen & Stappers 2008), which will alleviate the issue. At higher latitudes, the sampling in depth is more uniform, but unfortunately relatively sparse on angular scales (see next point).

• Small-scale DM structure: We have used the YMW electron model to translate the distances of pulsars to DMs, which has helped to stabilize our algorithm. The same model was also used in Hutschenreuter et al. (2022) as an input to their error correction routine, which we used in this work. The YMW model is a parametric electron density model that only considers the largest scales, apart from some local structures such as the local bubble. Combined with the spar-sity of pulsars at higher latitudes, we therefore expect that smaller structures at higher latitudes will be insufficiently constrained by pulsar data. A detailed discussion of the YMW model and its possible shortcomings is given in Ocker et al. (2021). We have tested the effects of the sparse spatial and angular sampling of the Milky Way by pulsars in Appendix B. These tests demonstrate that the insufficient sampling of the disk has precisely the effect discussed above, while in the high-latitude regions the underestimation only appears locally.

• Calculating EMs from H-α: The correction of the H-α emission for dust absorption is using a uniform mixing model (Dickinson et al. 2003) that includes a fudge factor, f_D, to account for the proportion of dust that lies in front of the H-α emitting gas. We have used f_D = 0.33 ± 0.1 in this work for the full sky, again according to Dickinson et al. (2003). It is likely that this estimate is wrong for some LoSs. Additionally, the electron temperature necessary for the conversion is not strongly constrained, which may introduce additional biases.

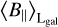• Correlation of n_e and By: The interpretation of ${\overline{B_{\Vert }}}_{\text{gal }}$ depends on this relation, as it can both over- or underestimate the more interesting quantity, ${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$ , depending on whether By is correlated or anticorrelated with ne. As is discussed in Sect. 2.2.1, there is considerable evidence that this relation holds for large portions of the sky, but it may break down; for example, along spiral arms.

To test the impact of these assumptions on our results, we ran two secondary inferences with either the RM or the EM branch left out. We refer to these inferences as EM-DM and RM-DM runs, respectively. These inferences have demonstrated that, while the overall scales of the respective inferred sky maps remain similar, the datasets have considerable impact on the small-scale structure.

All models (the main one and the two secondary ones) were evaluated using the geometric variational inference algorithm (geoVI) (Frank et al. 2021). In variational inference (VI), the posterior distribution (which in our case is a highly non-Gaussian distribution with several million dimensions) is approximated via a parameterized and analytically traceable distribution. The idea of VI is then to minimize the forward Kullback-Leibler divergence, a measure of similarity between probability distributions with regard to the parameters of this simpler distribution that yields the optimal VI approximation. In the particular case of geoVI, this distribution is implicitly defined via a parameterized invertible function that maps from the space where the model parameters are defined into a space where the approximate distribution is a standard normal distribution. This function is constructed using the Fisher information metric as a proxy for the curvature of the logarithm of the posterior. By ensuring that the metric and its first derivatives vanish at a given expansion point, the function is defined to map into a space where the posterior is locally close to a normal distribution. The coordinates of this expansion point constitute the parameters of the function and its optimal location is found by minimizing the KL. We note that this algorithm is an update to the metric Gaussian VI algorithm (Knollmüller & Enßlin 2019) used in Hutschenreuter et al. (2022). For a detailed discussion and comparison of the methods as well as a comparison to direct posterior evaluation, we refer the reader to Frank et al. (2021). Both MGVI and geoVI have been used successfully in the past for reconstructions of the Faraday sky (Hutschenreuter & Enßlin 2020; Hutschenreuter et al. 2022) and more general astrophysical (Leike & Enßlin 2019; Arras et al. 2022; Mertsch & Phan 2023; Scheel-Platz et al. 2023; Westerkamp et al. 2024; Edenhofer et al. 2024) and non-astrophysical (Guardiani et al. 2022; Reeb et al. 2023) contexts. We evaluated the resulting approximated posterior by drawing samples from it and report the corresponding empirical mean and standard deviations.

4 The results

In the following, we illustrate our results and compare them to existing work. All of the results have been inferred using the full model illustrated in Fig. 3, unless stated otherwise. All of the sky regions explicitly mentioned in the discussion are marked in Fig. 4. We show the full sky posterior mean maps of the 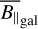${\overline{B_{\Vert }}}_{\text{gal }}$ (Fig. 5), DM_gal (Fig. 6), 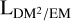${\text{L}}_{{\text{DM}}^2/\text{EM}}$, and ϱ_EM/DM (Fig. 7) skies. We discuss and illustrate our results on the 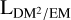${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky using a simplified model of n_e,gal in Fig. 8. The power spectra of the three main sky maps are shown in Fig. 9. We discuss two smaller sky regions (see Figs. 10 and 11) in Sect. 4.3 in more detail to compare our results to existing works. We further correlate the w_P factor with different external datasets in Sect. 4.4. The Faraday and EM sky maps (C.1) are discussed in Appendix C. We summarize the results of the secondary models in Appendix D. The logarithmic DM_gal skies for the two secondary models are shown in Fig. 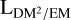D.1, while the ${\overline{B_{\Vert }}}_{\text{gal }}$ map from the RM-DM-run and the ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ map from the EM-DM-run are shown in Fig. D.2. The error bars quoted in the text are derived from posterior samples. Given the approximations made in the VI, these errors have to be considered a lower limit.

4.1 Sky maps

4.1.1 Magnetic field sky

The posterior mean of the LoS-averaged, LoS-parallel, and electron-density-weighted magnetic field sky is shown in Fig. 5. We record a root-mean-square (RMS) magnetic field value of 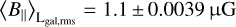${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}, \text{ms}}}=1.1\pm 0.0039\text{μG}$ averaged over the full sky. The map shows several distinct regions at higher latitudes with coherent LoS magnetic field strengths on the order of 2 µG. The sign pattern at high latitudes has long been studied (albeit in the RM sky) to find evidence for an axisymmetric spiral or bisymmet-ric spiral, which would point to evidence for the existence of a Galactic dynamo (see Dickey et al. 2022 for recent results in this regard and Brandenburg & Ntormousi 2023 for a review). Our results allow for a much clearer fit of 3D magnetic field models, since they also allow a fit of the amplitude. We shall attempt such a fit in future work. These reported magnetic field strengths are consistent with measurements of the large-scale magnetic field (Haverkorn 2015). We further validate our results for specific regions in the sky in Sect. 4.3.

The inner disk (i.e., the area within b = ±5° over the full longitude range) shows a similar RMS of 1.0 ± 0.0053 µG, but shows rather small-scale structures, which is consistent with a picture of many field reversals, which also lead to a suppression of the LoS-averaged disk field LoS component compared to the in situ values of the LoS component at typical disk locations. We note that the averaged LoS field strengths reported in the disk are most likely an overestimate of more than a factor of two, due to the fact that we do not probe the full Galaxy in DM with pulsars, and hence most likely underestimate DM_gal (see the discussions in Sects. 2.1.2 and 4.1.2 and also Fig. 6). There are prominent outliers in the disk and these contain the highest magnetic field strengths, found at (l,b) ≈ (48.2°,4.3°) with 5.4 ± 0.13 µG, and also at (l, b) ≈ (87.0°,–0.3°) with –4.5 ± 0.13 µG. The former excess is a consequence of the extremely strong RMs reported in this area (Shanahan et al. 2019), which lead to a similar excess in the Faraday skies of Hutschenreuter et al. (2022). The LoS associated with the former region corresponds roughly to the tangent of the Sagittarius arm (Vallée 2018). The reported 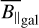${\overline{B_{\Vert }}}_{\text{gal }}$ excess might then be a result of the large-scale, uniform magnetic field aligned with the spiral arm in this region, as is already indicated in Shanahan et al. (2019) and supported by simulations (Reissl et al. 2020). We note that the 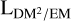${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky in Fig. 7 also indicates a high amount of ionized material in this region (see the discussions in Sects. 4.1.3 and 4.3.3).

Fig. 4 Specific sky regions that are discussed in more detail in the text. They correspond to (1) the Magellanic clouds, (2) the HII regions S2-27 and S2-7, (3) the Smith high-velocity cloud, (4) the Sagittarius arm region, and the north (5) and south (6) Galactic poles. We have used the logarithmic H-α EM data as the background.

Fig. 5 Posterior mean for the LoS-averaged parallel magnetic field of the Milky Way. The color scale is saturated at ±3. µG.

Fig. 6 Inference results for the Galactic DM sky, constrained by pulsar DM, free-free and Ha EM, and extragalactic Faraday data. Panel (a) shows the posterior mean and panel (b) the same result in logarithmic scaling. The color maps are saturated at 500 pc cm–3 and between 10 pc cm–3 and 1000 pc cm–3, respectively.

4.1.2 Dispersion measure sky

In Fig. 6, we show the results for the Galactic DM sky on both linear and logarithmic scaling. We find maximum DM values along LoSs at b = 0 and near the GC at l = 0, reaching 1.7 × 10³ ± 0.26 pc cm^-3. We find the minimum at higher latitudes, about 4.0 ± 0.26 pc cm^-3 at (1 ≈ 64.2°, b ≈ 68.5°). Most of the inner galactic disk exhibits values above 1000 pc cm^-3. The values in the disk are relatively low compared to, for example, the disk values predicted by Yao et al. (2017) or Cordes & Lazio (2002), which each predict DMs above 3000 pc cm^-3 in the inner disk, with the Galactic center reaching up to 4000 pc cm^-3. In Price et al. (2021), the typical fractional relative error on the distances predicted by the YMW electron model is estimated to lie between 0.35 and 2.76. Assuming that the DM error for the full Galaxy is on the same order of magnitude, our results would be narrowly compatible. But since pulsars with independent distances indicate that we do not probe the full Galaxy, it is highly likely that a significant tension in our results remains. We attribute this discrepancy to the insufficient volume sampling of pulsars in the Galactic disk and consider our results to be an underestimate by about a factor of two in the inner disk region, in line with the discussion in Sect. 3.3 and our tests in Appendix B.

Toward the Galactic poles, we can compare our results not only to the full Galaxy electron models of Yao et al. (2017) or Cordes & Lazio (2002), but also to local models of the Galactic disk (Gaensler et al. 2008; Ocker et al. 2020). The DMs calculated from these models in the Galactic pole regions are often reported as DM_⊥ = DM| sin(b)|; that is, the DM perpendicular to the Galactic plane, as in this projection the DM only depends on the Galactic scale height of the models. These models predict DM_gal,⊥ values between 18.9 ± 0.9pc cm⁻³ (Yao et al. 2017) and 25.6 ± 2.6pc cm⁻³ (Gaensler et al. 2008). We calculated mean values of DM_⊥ from our maps in the Galactic north and south pole regions above and below ±70° to compare with these results. We report 12 ± 0.15 pc cm⁻³ (north) and 13 ± 0.29 pc cm⁻³ (south) and note maximum values of 26 ± 0.28pc cm⁻³ and 25 ± 0.82pc cm⁻³ in the same respective regions. While the maximum values agree well with the other models, the mean values are considerably lower. Under the presumption that these numbers are straightforwardly comparable with the aforementioned model predictions, this would again indicate a slight underestimation of DM in our results, which might be explainable by the sparse sampling by pulsars at high latitudes, as is indicated by our tests with synthetic data, in Appendix B. Additionally, since the other models do not incorporate the small-scale structure as we do, it is possible that some subregions in the polar regions have a smaller DM than that predicted by the parametric models, which might be dominated by the pulsars with a larger DM.

Another explanation can be motivated by making a comparison with the logarithmic DM maps from the RM-DM and EM-DM runs in Fig. D.1. In the EM-DM run, we calculated mean values for DM_⊥ of 1.83 × 10¹ pc cm⁻³ (north) and 1.87 × 10¹ pc cm⁻³ (south), which are much closer to the predictions of the parametric electron models discussed before. A visual comparison reveals that there are regions of very low DM in both polar regions that are not present in the EM-DM run, indicating that these structures are driven by the RM data. These regions correspond to areas of increased magnetic field strength in Figs. 5 and D.2a. The RM data seems to be better explained by an increase in 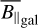${\overline{B_{\Vert }}}_{\text{gal}}$ and the EM data does not show such a correlation; hence, the DM maps are not affected in the EM-DM run. If our DM result in the polar regions is indeed underestimated, this may point to a significant B_‖ − n_e correlation, as the RM amplitude seems to be clearly driven by ${\overline{B_{\Vert }}}_{\text{gal}}$.

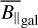Fig. 7 Inference results for the logarithmic ϱEM/DM (panel a) and ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ (Fig. b)) skies. Both quantities highlight different aspects of the ionized ISM (see Eqs. (11) and (12) for their definitions and Sect. 2.3.1 for the accompanying discussion). The ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky map is directly modeled in our work, while the ϱEM/DM map was calculated in a post-processing step.

Fig. 8 Sketch of the geometry proposed to explain the appearance of the ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky in Fig. 7. In a low-electron-density hot ISM (light orange), small but dense electron clouds are embedded (deep purple ellipses). The observer’s position is marked by the blue star symbol. An LoS at high galactic latitudes (blue arrow from top right) usually misses the dense clouds, and therefore probes the geometric length of the dilute ISM (long red bar) resulting in an ${\text{L}}_{{\text{DM}}^2/\text{EM}}~O(\text{kpc})$(kpc). An LoS in the Galactic plane (horizontal blue arrow) usually passes through at least one such cloud, and therefore probes their much smaller size (short red bars), leading to ${\text{L}}_{{\text{DM}}^2/\text{EM}}~O(10\text{pc})$(10pc). Some high-latitude LoSs pass through such clouds as well (blue arrow from top left) and exhibit a very short ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ as well (see short red bar next to that LoS). As high-latitude clouds need to be nearby to be within the thin Galactic disk, the set of LoSs passing through them span a larger area of the high-latitude sky. We note that the scales or shape of this illustration are not intended to realistically match the Milky Way.

4.1.3 The emission measure - dispersion measure conversion factors

In Fig. 7, we show the posterior means of ϱ_EM/DM and 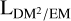${\text{L}}_{{\text{DM}}^2/\text{EM}}$ over the sky, defined in Eqs. (11) and (12). While the latter map is a direct result of the inference, the former was calculated in a post-processing step from posterior samples. As is detailed in Sect. 2.3.1, both quantities illustrate different aspects of the structure of the Galactic electron density, with ϱ_EM/DM being related to the average electron density within the emitting plasma and 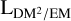${\text{L}}_{{\text{DM}}^2/\text{EM}}$ to its volume.

The ϱ_EM/DM sky shows variations between 9.6 × 10⁻³ ± 1.3 × 10⁻³ cm⁻³ to 17 ± 1.3 × 10⁻³ cm⁻³. The predominantly blue areas in this map show values around 0.1cm⁻³. This is consistent with the typical value assumed for the warm ionized ISM (Ferrière 2020), which indicates that the electron density is rather uniform (i.e., implying 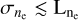${\sigma }_{n_{\text{e}}}\lesssim {\text{L}}_{{\text{n}}_{\text{e}}}$ in Eq. (12)) along these LoSs. Regions with ϱ_EM/DM ≫ 0.1 cm⁻³ are most likely dominated by strong fluctuations in electron density. Given the aforementioned consistency of ϱ_EM/DM with the literature value for n_e, we regard the former option as more likely in most cases.

Regarding the LDM2/EM map, we note that the map varies over orders of magnitude, from 21 ± 1.1 pc to 2500 ± 1.1 pc. Qualitatively, it appears to be a reliable tracer of turbulent structures on the sky as, for example, the inner Galactic disk, shock structures, and known HII regions all stand out with a small ${\text{L}}_{{\text{DM}}^2/\text{EM}}$. 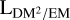We note that ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ in the thin inner disk is most likely overestimated by the same factor as the magnetic field estimate, as it is similarly indirectly affected by under-sampling of pulsars in the Galactic plane, as was discussed previously. On the other hand, several regions stand out with a large 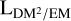${\text{L}}_{{\text{DM}}^2/\text{EM}}$. These are most notably the Sagittarius arms region, the halos of the Magellanic clouds, and the tail of the Smith high-velocity cloud (HVC), all marked in Fig. 4. It is notable that these regions are less discernible in the ϱ_EM/DM map, indicating that the high 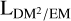${\text{L}}_{{\text{DM}}^2/\text{EM}}$ values trace regions with similar density but trace a larger volume than other regions.

In order to illustrate these interpretations, we show a simplified model of the ionized ISM in Fig. 8. In there, we assume the ISM to mainly consist of a rather uniform low-density plasma, in which small ionized regions of high n_e are embedded (e.g., HII clouds). All LoSs going through these small regions will have a small 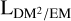${\text{L}}_{{\text{DM}}^2/\text{EM}}$, as the density along these LoSs shows large fluctuations. Assuming that the clouds have a similar density, ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ will be equal to the portion of the LoS within them. Since most of these embedded regions are located in the thin Galactic disk, some regions in the vicinity of Earth with a notable vertical offset will appear as extended regions at higher latitudes, again with a small ${\text{L}}_{{\text{DM}}^2/\text{EM}}$. 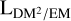Most high-latitude LoSs, however, will not go through such regions, and hence trace the more uniform low-density plasma. The ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ values will then agree with the physical length of the LoS. 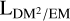The sketch also illustrates that ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ values of LoS not hitting high-density regions may still vary strongly with geometric effects; that is, by probing large structures outside (and not necessarily connected to) the thin disk. This may explain the large 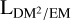${\text{L}}_{{\text{DM}}^2/\text{EM}}$ values toward the regions mentioned earlier. We devote a separate section (Sect. 4.3) to discuss effects related to such specific structures in more detail.

Fig. 9 Inferred angular power spectra of the ${\overline{B_{\Vert }}}_{\text{gal}}$ (panel a) and DMgal (panel b) sky maps. The colors indicate the different runs from which the spectra where calculated (for details, see Sect. 3.3).

4.2 Power spectra

We calculated the angular power spectra of the DM_gal and 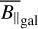${\overline{B_{\Vert }}}_{\text{gal}}$ skies in order to describe the statistical properties of our results and to compare the full model and the two secondary models. The results are shown in Fig. 9. We note that the spectra of the DM_gal skies do not capture their full statistics, due to the nonlinear nature of the DM_gal sky models. We have nonetheless opted to show the DM_gal power spectra instead of the Gaussian logarithmic DM_gal, as DM_gal is much more likely to be reported by both simulations and observations. In order to represent the power spectra concisely, we additionally fit the following parametric model as a function of the multipole, ℓ, $$C_{\ell ,fit}=\frac{A}{{\left({\ell }_0+\ell \right)}^{-s}},$$(21)

to the posterior power spectra with free parameters A, s, and ℓ₀, using the maximum a posteriori (MAP) method. We report on the fitted values in Table 1. Both the figures and the fits demonstrate that the power spectra show little variance between the different models. The most interesting parameter is the spectral slope parameter, s, as it gives information on the turbulent scaling of the underlying 3D quantities; that is, the magnetic field and the electron density. Chepurnov & Lazarian (2010) give an analytic formula to relate the power spectrum of a 3D isotropic and homogenous field to an integrated 2D angular spectrum, which essentially demonstrates that the spectral slope of a simple power law spectrum remains the same when projected on the sky under these idealized conditions and for ℓ > 15.

The Galactic disk most likely has different statistical properties than the higher-latitude regions, which breaks these assumptions. Due to the relatively small area occupied by the disk, the spectral slope inferred here will be dominated by these higher-latitude regions. The values found for s in the DM case are all somewhat close to 11/3 = 3.67, indicating Kolmogorov turbulence in the fluctuations of the electron density distribution. This is consistent with the “big power law in the sky;” that is, other tracers of the spectral slope of the nearby n_e that have shown its Kolmogorov-like behavior over many orders of magnitude (Armstrong et al. 1995; Ferrière 2020). The spectral slope of the 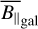${\overline{B_{\Vert }}}_{\text{gal}}$ sky is generally flatter, which might be a result of magnetic field reversals that introduce sharp edges in the map. Another possible explanation might be a spectral flattening of the 3D spectrum of the magnetic field, marking the injection scale of the Kolmogorov spectrum. Such an effect has been observed by Minter & Spangler (1996) for a high-latitude region using point-source RM data and Hα-derived EM data. The flatter-than-Kolmogorov angular spectrum observed in our case may then stem from an averaging effect over different spatial scales of this “broken” power law. While this is a plausible explanation, it should be noted that the electron density power spectrum is also conjectured to flatten above a certain scale, albeit with some controversy about the actual value (most likely between 3 and 100 pc (Ferrière 2020)). The fact that we do observe a Kolmogorov spectrum for DM_gal but not for 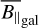${\overline{B_{\Vert }}}_{\text{gal}}$ might then point to a larger injection scale for turbulence in the electrons, which decreases the impact of the flatter parts on the angular spectrum. We note that we do not directly observe a spectral break in any of the angular power spectra, which can be explained by the fact that different 3D scales are averaged to the same angular scales, thereby smoothing out any breaking scale.

4.3 Specific objects on the sky

The physical assumptions of our model laid out in Sect. 3.3 are based on our general understanding of the diffuse ionized ISM. To compare our results, we have selected regions that have already been subject to similar analyses to infer B_‖ from RM and DM or EM measurements, and hence provide an ideal testing ground. In the following, we analyze two exemplary regions on the sky, corresponding to two different physical environments at intermediate latitudes; namely, the HII region Sh2-27 and the Smith HVC. An additional incentive to choose these regions comes from their apparent extreme values in ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ visible in Fig. 7, indicating very different physical environments. At the end of the section, we also comment on the Magellanic clouds and the Sagittarius region in the Milky Way.

4.3.1 Sh 2-27

Sh 2–27 is a prominent HII region centered at approximately (l, b) = (6°, 23°) and is easily discernible as a distinct region of negative RM above the Galactic center in the Faraday map (Fig. C.1a). We show cutouts of the 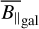${\text{L}}_{{\text{DM}}^2/\text{EM}}$, ${\overline{B_{\Vert }}}_{\text{gal}}$ and ϱ_EM/DM skies corresponding to this region in Fig. 10. Figure 10a seems to reliably trace the region as a compact object of low L_DM²/EM, indicating a high level of turbulence. We find a minimum value of 22 ± 1 pc for 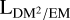${\text{L}}_{{\text{DM}}^2/\text{EM}}$, which is much lower than the immediate surroundings that show values well above 100 pc, but consistent with the size of the HII cloud of 35 pc at distance of 160 pc (Thomson et al. 2019).

Within the area of the cloud, we find minimum magnetic field strengths in Sh 2-27 of −4. ± 0.16 µG (Fig. 10b) and an RMS of 2.12 ± 0.048 µG. For ϱ_EM/DM, we find values up to 3.5 cm⁻³ (Fig. 10c). The mean DM is 88.4 ± 1.61 pc cm⁻³, with a maximum of 120 ± 4.7pc cm⁻³. We find six pulsars within or very close by the boundary of Sh 2-27. A comparison of their DM with the full DM sky reveals that four of them seem to have a similar or higher DM as Sh 2-27, indicating that they most likely lie behind the region. For one of them (PSR J1643-1224), this is confirmed by independent distance measurements, as was already found by Harvey-Smith et al. (2011). In order to calculate the average magnetic field strength within the HII cloud 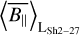${\langle \overline{B_{\Vert }}\rangle }_{{\text{L}}_{\text{Sh}2-27}}$, one has to subtract any potential fore- and background 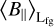${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{fg}}}$ that impacts the LoS average. Indeed, Thomson et al. (2019) have found considerable magnetized foreground structure in diffuse RM in the LoS toward Sh 2-27, which they attribute to the Local Bubble and several ionized dust clouds. In order to provide a rough estimate for 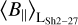${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{Sh}2-27}}$, we assume that 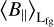${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{fg}}}$ is similar in the close environment to the HII clouds, which is dominated by a large diffuse region with about 0.5 µG. If we additionally assume no correlation between n_e and B_‖, the aforementioned size of the HII cloud of 35 pc at a distance of 160 pc (Thomson et al. 2019), and the mean value for 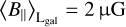${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}=2\text{\hspace{0.17em}µG}$ in the region, a back-of-the-envelope calculation gives $${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{Sh}2-27}}=\frac{{\text{L}}_{\text{gal}}}{ {\text{L}}_{\text{Sh}2-27}}\left({\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}-{\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{fg}}}\right)+{\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{fg}}}\approx -11\text{μG}.$$(22)

Repeating the same exercise as above for ϱ_EM/DM gives 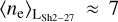${\langle n_{\text{e}}\rangle }_{{\text{L}}_{\text{Sh}2-27}}\approx 7$ cm⁻³. We can compare these values to previous analyses of Harvey-Smith et al. (2011) and Raycheva et al. (2022). The former reference uses 57 extragalactic RMs to constrain the magnetic field strength and find a median value of −6.1 ± 2.8 µG. Similarly, Raycheva et al. (2022) have analyzed the region using diffuse polarized radio emission and find a median magnetic field strength of −4.1 ± 0.1 µG, with a maximum near −9 µG. Both works use H-α EMs to constrain the electron density and assume that Sh 2–27 has close to spherical geometry, with an LoS path length of about 35 pc, and a filling factor, 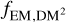$f_{\text{EM},{\text{DM}}^2}$, of 0.2. We show both the magnetic field estimate and projected geometry of the HII region from Raycheva et al. (2022) in Fig. 10d. Regarding the electron density, Harvey-Smith et al. (2011) and Raycheva et al. (2022) find 10.6 cm⁻³ and 8.2 cm⁻³, respectively, which is higher than our estimate. It should be mentioned that in the latter reference, if the elliptical model used in this work is aligned with the LoS, the predicted average electron density lowers to 7.3 cm⁻³.

It is possible that the difference in the magnetic field and electron density estimates can be attributed to our very simple foreground estimation. There are also some notable differences in modeling, as both Harvey-Smith et al. (2011) and Raycheva et al. (2022) assume all dust to lie in front of the HII region (i.e., assuming ƒ_D = 1 in Eq. (14) in contrast to 0.33 used in this work), which increases their estimate of the EM of Sh 2– 27 by a factor of 2–5 compared to our work, depending on the amount of observed dust. This implies an increase in their estimate of the electron density in the cloud, and in turn decreases their magnetic field estimate compared to our work. We note that the Planck mission also predicts on the order of 300 pc cm⁻⁶ for the EM, in line with the 360 ± 29 pc cm⁻⁶ found in this work. However, we note that the low Planck EM may suffer from the same bias stemming from the treatment of dust emission in the astrophysical component separation of the microwave sky.

4.3.2 Smith cloud

The Smith cloud is an HVC on the southern sky, centered on (l, b) = (42°,−16°), at a distance of 12.4 ± 1.3 kpc (Lockman et al. 2008). The cloud covers a large portion of the sky, with an (l, b) = (39°, −13°) nose pointing toward the Galactic disk and a tail extending well past (l, b) = (45°, −20°) (Hill et al. 2013). We show cutouts of ${\text{L}}_{{\text{DM}}^2/\text{EM}},\overline{B_{\Vert }}$ and ϱ_EM/DM in this sky region in Fig. 11. In it, we illustrate the shape of the cloud using HI data from the Green Bank Telescope (Lockman et al. 2008) (Fig. 11). While the nose seems to be barely magnetized, the tail shows relatively strong excesses in extragalactic RMs (Hill et al. 2013; Betti et al. 2019), indicating significant magnetization. Within the tail region, we derive magnetic field strengths between 5.5 ± 0.18 µG and −2 ± 0.13 µG and identify three compact subregions with alternating signs in the magnetic field map (Fig. 11b), roughly separated by longitude lines 49° and 41 °. These regions align very well with ridges seen in the HI data, which is consistent with the picture of the cloud falling into the Galaxy, leaving behind an ionized tail. For a more detailed discussion on geometry and physical effects, we refer the reader to Betti et al. (2019). We estimate LoS-averaged magnetic field strengths of approximately 2, −1.5, and 2.5 µG in these subregions, ordered with decreasing longitude. These compact regions have been studied as well by Betti et al. (2019) (their regions 3,4, and 5), who estimated lower limits of 2.86 ± 0.3 µG, −1.35 ± 0.2 µG and 5.33 ± 0.3 µG within these regions, respectively. Hill et al. (2013) estimated a maximum magnetic field strength of 8 µG in the Smith cloud. Given the large angular size and distance of the cloud, we have refrained from performing a foreground estimation as we did for the Sh2-27 HII region, but only note the good correspondence of the sign patterns between our work and Betti et al. (2019), as well as the very precise alignment with the HI data for the ridges. In our work, the tail region is also noticeable as an area of strongly increased ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ in Figs. 7 and 11, reaching values of 2.5 × 10³ ± 150 pc. 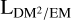We note that the Smith cloud is naturally not constrained directly by pulsars, which makes our DM (and therefore ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ and ϱ_EM/DM) estimate rather uncertain.

The examples of Sh 2-27 and the Smith HVC demonstrate that our method is in agreement with known results even in such extraordinary environments, but also that our results cannot be interpreted without a careful consideration of the particularities of the region in question; for example, the Galactic foreground and background or the pulsar coverage.

Fig. 10 Cutouts of several sky maps toward the HII region Sh 2-27. The images show a) ${\text{L}}_{{\text{DM}}^2/\text{EM}}$, b) ${\overline{B_{\Vert }}}_{gal}$, c) ϱEM/DM, and d) the foreground reduced B‖gal image from Raycheva et al. (2022), which is derived from diffuse polarized radio emission. The contours of the latter image are plotted over the first three images, with contour lines set at −2 µG (light blue) and −6 µG (dark blue). The elliptic boundary in d) indicates the projected boundaries of Sh2-27 assumed in Raycheva et al. (2022).

Fig. 11 Cutouts of several sky maps toward the Smith HVC. The images show a) ${\text{L}}_{{\text{DM}}^2/\text{EM}}$, b) ${\overline{B}}_{\Vert \text{gal }}$, c) ρEM/DM, and d) velocity-integrated HI observed by Justify the Green Bank Telescope (Lockman et al. 2008). Contours of the HI data are plotted over the first three images, with contour lines set at 30 K km s−1 (light violet) and 60 K km/s (dark violet).

4.3.3 Other regions

The halo of the Magellanic clouds is also noticeable in the ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky map. Their angular sizes are visually consistent with the denser parts of the Magellanic corona found by Krishnarao et al. (2022). Regarding a quantitative comparison, Smart et al. (2019) give values of several kpc for the physical size of the tail region of the SMC (i.e., the region pointing toward the LMC), while we report a maximum of 700 pc in ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ in the same area. Given that ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ is a lower limit on the physical size, this indicates consistency.

As for the Sagittarius arm region (defined by the tangent point of the Sagittarius arm at l = 49° and b = 0°, also marked in Fig. 4), this also displays very large values in ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ just a few degrees above and below the disk in latitude. As was mentioned before, this region also exhibits the strongest RMs and LoS-averaged magnetic field, also pointing to a coherent magnetic field configuration with minimal averaging along the LoS. However, the picture is obfuscated somewhat by the fact that it also contains the most significant tension between the H-α and free–free EMs, with the H-α estimate two orders of magnitude larger than the Planck data, which points to strong systematic effects in one or both of the EM estimation techniques that might have affected our results in ${\text{L}}_{{\text{DM}}^2/\text{EM}}$.

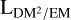Fig. 12 Scatter plots of pulsar observables vs. the respective inferred Galactic values. The coloring indicates the posterior mean of the wP parameter introduced in Eq. (19). Figs. (a) and (b) illustrate the RMp – RMgal correlation at high and low latitudes, respectively. Figs. (c) and (d) illustrate the correlation of the pulsar temporal broadening parameter, τsc , with DMgal and ϱEM/DM , respectively.

4.4 Correlations to other pulsar observables

Pulsars not only provide DM measurements, but a significant fraction also come with RM data (about 12%) and data on interstellar turbulence via, for example, measuring the temporal broadening, τ_sc , of pulses (again about 12% of all pulsars).

The pulsar RM data is not immediately suitable for our algorithm, as the modeling of the residual Galactic component is not possible with a simplistic effective model, unlike the pulsar DM in Eq. (19). Nonetheless, this data is of course still informative about the Galactic ISM. The pulsar RMs are compared to the respective RM values of the full Galaxy at the same LoS in Fig. 12a and Fig. 12b, in which we separate the data into high- and low-latitude pulsars. The plot reveals that high-latitude pulsar RMs show a good correlation (Pearson-r: 0.82) with the Galactic RM, indicating that they probe the same magneto-ionic medium. This implies that our DM predictions in this region should not suffer strongly from the insufficient sampling of the ionized volume of the Milky Way. At lower latitudes, the correlation vanishes (Pearson-r: 0.004), which is consistent with only a small volume probed by the pulsar RM. In both cases, the posterior w_P factor defined as the relative DM occupied by the pulsar in Eq. (19) is in better correlation with the full respective population of the pulsar RM. This indicates that the w_P factor is at least a good qualitative indicator of the fraction of the LoS probed by a pulsar.

In Figs. 12c and 12d, we correlate τ_sc with the DM_gal and ϱ_EM/DM skies. This quantity is directly proportional to the scattering measure (SM), which is defined as the LoS integral of the square n_e fluctuation amplitude, and hence a good tracer of variability along the LoS (see e.g., Ferrière 2020 for a summary). We expect it to be positively correlated with σ : n_e (i.e., more variations lead to more scattering), the DM (more material, more scattering), and with the length of the LoS due to the integral. The DM is correlated with τ_sc , which is consistent with previous findings (Rickett 1977; Krishnakumar et al. 2019). This effect can in simple terms be explained as more material leading to more scattering in the interstellar plasma, the details depending on the correlation structure of the electron density field. The plot furthermore reveals that for a certain DM_gal found at the position of a pulsar, a smaller w_P tends to imply a smaller τ_sc . Since w_PDM_gal gives the pulsar DM that produces the scattering, this simply confirms that smaller w_P indeed probe smaller portions of the respective LoS. Considering only the pulsars with w_P ≈ 1, τ_sc increases with a slope of about 2 below ≈100 pc cm⁻³, which is in general agreement with the literature (Rickett 1977; Krishnakumar et al. 2019). For larger DM values, the slope steepens. As pulsars with such high DMs are mostly placed in the disk, their DM_gal is most likely underestimated, in line with the discussions in Sects. 3.3 and 4.1.2, which would explain the steepening.

The correlations of both τ_sc and wp with ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ are approximately zero, and are hence not shown here. The ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ factor is inversely proportional to ${\sigma }_{n_{\text{e}}}$ but linearly proportional to the length of the LoS, which explains this lack of correlation. The ϱ_EM/DM factor, however, shows an almost linear relation with τ_sc on a log–log scale, which is fit well by ${\tau }_{\text{sc}}\propto {\varrho }_{\text{EM}/\text{DM}}^{3.5}$. According to Eq. (12), this fraction is proportional to ${\sigma }_{n_{\text{e}}}$ in the case of strong variability along the LoS. Since 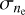${\sigma }_{n_{\text{e}}}$ is also directly related to the SM, this plot demonstrates the strong n_e variations along the LoS probed by pulsars.

We would like to emphasize that Figs. 12c and 12d correlate the observed pulsar data with inferred Galactic quantities (which trace the full LoS). This explains the much higher scatter of τ_sc per DM observed in these plots, in contrast to, for example, τ_sc − DM_P analyses (see e.g., Krishnakumar et al. 2019). All plots in Fig. 12 also show that the w_P factors are approximately one for a large portion of pulsars, which, at least in the disk where most pulsars are found, is most likely not true as most pulsars are known not to probe the full Galaxy. This again indicates that the inferred DM_gal sky at low absolute latitudes is underestimated. We hence deem our results for w_P in this area to provide an upper limit, and postulate that many values are most likely overestimated by at least a factor of two at low latitudes, again in line with the discussions in Sects. 3.3 and 4.1.2.

5 Summary and outlook

In this work, we have used several datasets in order to disentangle the Galactic Faraday sky into physical components; namely, the averaged LoS parallel and electron-density-weighted magnetic field component and the DM, both for the full sky.

To constrain the DM, we have relied on pulsars and additionally on EM data stemming from collisional processes, which also opens a path to constrain the structure of ionized plasma of the Milky Way.

We have chosen to model all sky maps non-parametrically; each pixel is only constrained by data and a priori assumptions about the all-sky correlation structure. This allows us to represent Galactic structures in unprecedented detail, especially in comparison to existing parametric models of the Galactic magnetic field or the electron density.

At mid to high latitudes we find average magnetic field values of around 2 µG, consistent with local measurements. The morphology of the map in Fig. 5 indicates the strongest LoS-averaged magnetic field in mid-latitude regions outside the turbulent Galactic disk. In the same regions, the DM values gradually decrease with absolute latitude toward a minimum between 10 and 20 pc cm⁻³ at the poles. A comparison with previously published models and independent datasets reveals that our results agree well with previous findings in these regions. In contrast, the DM results in the disk (with a maximum of 1.7 × 10³ pc cm⁻³) appear to be too small by at least a factor of two, if compared to other models. This is easily explained by the insufficient volume sampling of the Galactic disk by pulsars, which we have not corrected for. This is a deliberate modeling choice, which accepts this systematic error in order to not have to rely on strong assumptions about the structure of the Milky Way. It should be noted that this error translates onto all other sky maps inferred in this work; in particular, the magnetic field estimate in the disk is too large by the same factor.

In addition to our results for the Galactic magnetic field and the DM sky, we have derived several results for the structure of the electron density of the Milky Way. We inferred angular power spectra for all our sky maps, which in the case of the DM sky reveals a Kolmogorov-like behavior, in accordance with the big power law in the sky (Armstrong et al. 1995). Additionally, we have defined two conversion factors to link the DM and EM skies; namely, 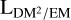${\text{L}}_{{\text{DM}}^2/\text{EM}}$ (in Eq. (11), as the ratio between squared DM and EM) and ϱ_EM/DM (in Eq. (12), as the ratio between squared DM and EM). The former factor gives the approximate portion of the LoS effectively contributing to EM and DM via high densities, implying that it is equal to the length of the LoS in the special case of a uniform medium and in general a lower limit to it. In a similar vein, ϱ_EM/DM gives the average electron density along the full LoS in the approximately uniform case. Both maps agree well with literature values for the Milky Way.

We have devised a simple illustrative mock model of the Galactic electron density, which allowed us to explain this phenomenology in terms of simple assumptions about the 3D distribution of electrons. We have also shown a detailed analysis of two cutouts of the sky, centered on the HII cloud Sh 2–27 and the Smith HVC. A comparison to previous works on these objects reveals good correspondence, but also demonstrates the need for a detailed foreground analysis, if the properties of peculiar objects were to be analyzed with our method.

Our results still suffer from several unaccounted-for potential biases in our model and the datasets we use, which we have partly verified. These are the mainly large systematic uncertainties in the EM data derived from Hα, which mostly stem from the unknown relation to the Galactic dust distribution, as well as the sparse volume (at low latitudes) and angular (at high latitudes) sampling of pulsars.

The road ahead to improve our results must clearly be focused on alleviating these issues, which can be achieved by going down two main paths. First, the inclusion of new datasets will be helpful. Potential additions are mostly dust data, which would increase the fidelity in the Hα derived EM data, as well as new pulsar data coming from next-generation radio telescopes such as the Square Kilometer Array that are projected to be able to observe almost all Galactic pulsars (van Leeuwen & Stappers 2008; Keane et al. 2015). A second possible data source that may reduce the systematic biases stemming from the pulsar distribution is fast radio bursts (FRBs), which it has already been demonstrated allow for such an analysis (Pandhi et al. 2022) (see also Cook et al. (2023) and Ravi et al. (2023) for illustrations of the potential value of FRBs for the inference of the Galactic electron density). FRB DMs provide a nice complementary dataset to the pulsar DMs as they yield an upper limit to the DM, in contrast to the lower limit provided by pulsars.

The second path to improving our results concerns modeling. A common denominator for many of the shortcomings of our results is that they originate in some systematic effect along the LoS; for example, via some selection effect in probing the Galactic volume or an unclear correlation of Galactic components before the LoS integration (e.g., ρ_Dust − n_e correlations). Additionally, the interpretation of our results often requires an assumption about properties of the 3D structure of the Milky Way; for example, with regard to the B_∥−n_e correlation or the turbulent properties of the electron density to explain the 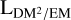${\text{L}}_{{\text{DM}}^2/\text{EM}}$ factor. It hence seems clear to us that a full resolution of these effects can only be achieved by inferring the full 3D volume for both the interstellar plasma and the associated magnetic field, as has been envisioned by, for example, Boulanger et al. (2018).

Data availability

The results are accessible at https://zenodo.org/records/10523170, and at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/A314

Acknowledgements

We would like to thank the referee for a constructive report. Furthermore, we would like to thank Valentina Vacca for helpful discussions and Jay Lockman and Sarah Betti for providing the GBT HI data. The following python packages were used in this work: Numpy (Harris et al. 2020), Scipy (Virtanen et al. 2020), Nifty (The NIFTy5 team et al. 2019), ducc, cmasher (van der Velden 2020), astropy (Astropy Collaboration 2022) and h5py (Collette 2013). SH and MH acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2002 research and innovation programme (grant agreement no. 772663). PF acknowledges funding through the German Federal Ministry of Education and Research for the project ErUM-IFT: Informationsfeldtheorie für Experimente an Großforschungsanla- gen (Förderkennzeichen: 05D23EO1). NR acknowledges funding from the joint NWO-CAS research programme (project number 629.001.022) in the field of radio astronomy, which is (partly) financed by the Dutch Research Council (NWO).

Appendix A Sky priors

Here, we summarize the priors on the ${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$ , DM_gal and L_EM,DM sky models. As discussed in Sect. 3, these are modeled as (log-formal processes with an unknown correlation function, for which we set a priori constraints, following the generic model developed in (Arras et al. 2022). In the specific instance of correlations on the unit sphere, this model aims to represent a field s via $$s=m_0+\left({\sigma }_0+{\sigma }_{\sigma ,0}{\xi }_{\sigma }\right){\xi }_0+ℱ\left(\sqrt{T_{\ell }\left({\xi }_T\right)}{\xi }_{\ell }\right).$$(A.1)

where the global mean of the field is modeled via the first three terms with hyperparameters m₀,σ₀ and σ_σ0. The second part encodes the correlation structure of the field, with 𝓕 denoting the spherical harmonic transform and T_ℓ an angular correlation kernel. The excitation terms ξ_x form the parameter space of the model that is constrained in the inference and are a-prior standard normal distributed, while the hyperparameters encode a priori assumptions on the correlation function. The kernel is modeled via $$\sqrt{T_{\ell }}=\frac{e^{m_a+{\sigma }_a{\xi }_a}}{N}\mathrm{Exp}*e^{\left[\left(m_s+{\sigma }_s{\xi }_s\right)\ln (\ell )+f\left(m_{\eta },{\sigma }_{\eta },{\xi }_{\text{Φ}}\right)\right]},$$(A.2)

where have borrowed the notation of Leike et al. (2020), in that Exp* is denoting exponentiation of the coordinates, i.e., going from log(ℓ) to ℓ. This equation parametrizes a power law in log–log space with the slope modeled by m_s and σ_s terms, amplitude modeled by the m_a and σ_a terms, the normalization of the power spectrum N and an additional term f responsible for deviations from the power law. We do not write out f and N here to keep our notation simple, but refer to Arras et al. (2022) for details. This field model depends on hyperparameters (m₀, σ₀, σ_σ0, m_s, σ_s, m_a, σ_a, m_η, σ_η). We summarize our choice of hyperparameters in Table .1.

The hyperparameters of the model are chosen such that mean and variance of the overall resulting field models easily cover the plausible scales for each of the three physical quantities, as discussed Sect. 2, in order to not bias the inference. The width of the priors is also often limited by numerical issues, as the exponentiation and multiplication of fields easily produces values beyond what is numerically representable. This has limited the possible variance of the log(DM_gal) and $\log \left({\text{L}}_{{\text{DM}}^2/\text{EM}}\right)$ priors somewhat, but as illustrated in Fig. A.1, the relevant physical scales are still well represented. The figure shows four samples for each model. The morphology of the sky maps illustrate the strong variability in smoothness the priors allow. We also show histograms of the sky values of the four samples and a combined set of 100 sampled sky maps for each model, illustrating the wide range of a priori allowed values, easily encompassing the ranges discussed in Sect. 3.

Fig. A.1 Illustrations of the priors used for the ${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$ , DMgal and ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky models. The right side shows sky maps corresponding to four different samples drawn from the respective prior distributions. The left side shows histograms of the same prior samples, and additionally a line summarizing the distribution of values over 100 samples. The histograms were normalized to unity to ensure comparable scales.

Appendix B Tests with synthetic data

In this section we demonstrate the impact of selection effects in the observed spatial pulsar distribution, as well as our assumption of a-priori Gaussianity for the B_‖gal, log-DM_gal and 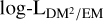$\log {\text{-L}}_{{\text{DM}}^2/\text{EM}}$ skies. To this end, we generated synthetic data using the following recipe:

1. We draw random sky maps for the B_‖gal, DM_gal and 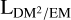${\text{L}}_{{\text{DM}}^2/\text{EM}}$ skies using the Arras et al. (2022) correlation model assuming a Kolmogorov spectrum for all three random maps.

2. We generate a profile template of the large scale features of the Galaxy using the YMW electron model. We multiply the synthetic DM map with this template, and accordingly divide the synthetic 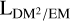${\text{L}}_{{\text{DM}}^2/\text{EM}}$ map with it. This imprints the shape of the large scale Milky Way features on the data, making the synthetic date more realistic. Furthermore, features such as the thin disk are rather unlikely in our isotropic prior models, making their reconstruction an additional challenge for this test.

3. We adapt the hyperparameters of the Arras et al. (2022) correlation model, such that the synthetic RM, DM and EM roughly show values expected for the Milky Way.

4. We draw random angular positions for the extragalactic RMs and the Galactic pulsar DMs and distribute the former uniformly over the sky, while we scale the density of the latter with |l|^1.5 and |b|^2.5, reflecting the Galactic origin of pulsars. We note that this results in a relative overdensity of pulsars at l = 0 at higher latitudes, which is clearly not mirroring the real distribution, but serves as a proxy for a possible observational selection bias. We choose to draw positions for 50000 RMs, roughly the same as we have available in the Van Eck et al. (2023) catalog. In case of the pulsars, we distinguish two cases:

   1. 30000 pulsar positions (l_i, b_i), with the respective DM drawn uniformly between 0 and the respective Galactic DM value at (l_i, b_i), henceforth called the ideal case.

   2. 3000 pulsar positions (l_i, b_i), with the respective DM drawn uniformly between 0 and min (DM_gal (l_i, b_i), 1000 pc cm⁻³), henceforth called the realistic case.

   In the first case, we effectively sample the full Milky Way, albeit in an inhomogeneous way. The second case is closerto reality, as the number of pulsars is closer to what is available in the ATNF catalog, the high latitude regions are sparsely sampled and the high DM values of the disk are not probed. We emphasize the 1000 pc cm⁻³ limit is just a proxy for the real selection effect, as in reality pulsars observations are limited by luminosity and not DM.

5. We draw error bars uniformly between 1 and 10 % for the RM and the full sky EM data, and between 0.1 and 1 % for the pulsar DM. This reflects the very low observational errors of pulsar DMs, as discussed in Sect. 2.1.2.

The resulting synthetic datasets are shown in Fig. B.1. We then run the inference procedure of Sect. 3 using precisely the same set up, i.e., the main model with the same set of hyperparameters. The inferred sky maps and the synthetic truth are shown in Fig. B.2. While we recover the general morphology of the maps very well, especially in case of the ideal pulsar dataset. However, the results constrained using the realistic pulsar DM dataset clearly underestimate the Galactic DM amplitude in the disk, and this effect is translated in the B_‖gal and $\log {\text{-L}}_{{\text{DM}}^2/\text{EM}}$ maps. The high latitude DM is severely underestimated in certain spots, while other areas appear to be fine. We conclude that the disk DM in our case is likely strongly underestimated, and that this effect can also exist at higher latitudes, albeit much less pronounced.

Fig. B.1 Synthetic datasets produced according to the procedure outlined in Sect. B. The plots show projections on the sky for the ideal (panel a) and realistic (panel b) cases of pulsar DM, as well as the RM (panel c) and EM data (panel d) sets.

Fig. B.2 Ground truth and inference results for the synthetic data. The left column shows the ground truth for the B‖gal, log-DMgal and $\log {\text{-L}}_{{\text{DM}}^2/\text{EM}}$ skies. The middle and right column show the corresponding results for the ideal and realistic cases of pulsar DMs, respectively.

Appendix C Faraday and EM sky maps

For completeness, we show the results of the Faraday rotation sky and logarithmic EM sky in Fig. C.1. The general agreement with the results obtained by Hutschenreuter et al. (2022) and HE20 is good, which gives an important validity check for our method.

Fig. C.1 Inference results for the Galactic Faraday and EM skies. Panel (a) shows the posterior mean for the Faraday sky, while panel (b) shows the posterior mean for the logarithmic EM sky.

Appendix D Secondary models

In order to test our results on the dependence, we have run two secondary models, where we have turned off either the RM or EM branch (see Sect. 3). We show the respective logarithmic DM_gal skies in Fig. D.1. These sky maps and the correspondent result for the full model (see Fig. 6b) reveal that, while the overall scales are similar, several structures and can be clearly associated with either the RM or EM datasets. Most filamentary structures can be attributed to the H-α dataset, as they are mostly missing in the RM-DM run. Conversely, the RM-DM map appears much more granular structure. We attribute this to the fact that this run was only constrained by point measurements (i.e., extra-galactic RMs and pulsar DMs) and not by the (almost) full sky EM dataset, which lead to a much worse constraint on small scales. Toward the poles, the RM data seems to favor much lower DM values as the EM-DM map. The 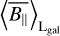${\langle \overline{B_{\Vert }}\rangle }_{{\text{L}}_{\text{gal}}}$ map reveals coher-ent structures which seem to have absorbed some of the DM amplitude, see the discussion in Sect. 4.1.2 for more details.

Fig. D.1 Inference results for the logarithmic Galactic DM sky of the secondary models introduced in Sect. 3.3. Panel (a) shows the posterior mean of the logarithmic DMgal sky constrained only by RM and DM data, and panel (b) the corresponding result constrained only by DM and EM data.

Fig. D.2 Inference results of the secondary models introduced in Sect. 3.3. Panel (a) shows the posterior mean of the sky constrained only by RM and DM data, and panel (b) the filling factor sky constrained only by DM and EM data.

References

All Tables

All Figures

Fig. 1 Sky projections of all datasets used in this work. These are pulsar DMs from the ATNF catalog (panel a; Manchester et al. 2005), RMs stemming from the van Eck catalog (panel b; Van Eck et al. 2023) and the EMs calculated from free–free (panel c; Planck Collaboration X 2016) and H-α (panel d; Finkbeiner 2003) emission. The latter two datasets are shown on a logarithmic scale. We show the quality masks employed for the EM data (see the discussion in Sect. 2.3.2) in panels (e) and (f), with 0 indicating a masked pixel. These and all of the following sky maps are presented in Galactic coordinates centered at (l, b) = (0°, 0°), with longitude increasing to the left.

In the text

Fig. 2 Illustration of the EM-DM relation for two simple models, discussed in Sect. 2.3.1. The red graph shows a short LoS with relatively weak variations in ne, while the blue one shows a long LoS with strong variations. Albeit depicting two completely different environments, the calculated DM, EM, and ${\text{L}}_{{\text{DM}}^2\text{/EM}}$ values for an observer sitting at L = 0 approximately agree. The units in this illustration are arbitrary, as the effect is scale-invariant. Its main intention is to demonstrate the interpretational limitations of Eq. (11). A more physical illustration of the Milky Way is provided later in Sect. 4.1.3.

In the text

	Fig. 3 Graph illustrating the hierarchical Bayesian model employed in this work. The sky models in the upper layer correspond to the Gaussian fields, ψ,ρ, and χ, in that order. This graph omits several layers at the top, which are similar for each Gaussian field and contain the correlation structure modeling. For details on those, see Appendix A and Arras et al. (2022).
In the text

	Fig. 4 Specific sky regions that are discussed in more detail in the text. They correspond to (1) the Magellanic clouds, (2) the HII regions S2-27 and S2-7, (3) the Smith high-velocity cloud, (4) the Sagittarius arm region, and the north (5) and south (6) Galactic poles. We have used the logarithmic H-α EM data as the background.
In the text

	Fig. 5 Posterior mean for the LoS-averaged parallel magnetic field of the Milky Way. The color scale is saturated at ±3. µG.
In the text

	Fig. 6 Inference results for the Galactic DM sky, constrained by pulsar DM, free-free and Ha EM, and extragalactic Faraday data. Panel (a) shows the posterior mean and panel (b) the same result in logarithmic scaling. The color maps are saturated at 500 pc cm–3 and between 10 pc cm–3 and 1000 pc cm–3, respectively.
In the text

Fig. 7 Inference results for the logarithmic ϱEM/DM (panel a) and ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ (Fig. b)) skies. Both quantities highlight different aspects of the ionized ISM (see Eqs. (11) and (12) for their definitions and Sect. 2.3.1 for the accompanying discussion). The ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky map is directly modeled in our work, while the ϱEM/DM map was calculated in a post-processing step.

In the text

Fig. 8 Sketch of the geometry proposed to explain the appearance of the ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky in Fig. 7. In a low-electron-density hot ISM (light orange), small but dense electron clouds are embedded (deep purple ellipses). The observer’s position is marked by the blue star symbol. An LoS at high galactic latitudes (blue arrow from top right) usually misses the dense clouds, and therefore probes the geometric length of the dilute ISM (long red bar) resulting in an ${\text{L}}_{{\text{DM}}^2/\text{EM}}~O(\text{kpc})$(kpc). An LoS in the Galactic plane (horizontal blue arrow) usually passes through at least one such cloud, and therefore probes their much smaller size (short red bars), leading to ${\text{L}}_{{\text{DM}}^2/\text{EM}}~O(10\text{pc})$(10pc). Some high-latitude LoSs pass through such clouds as well (blue arrow from top left) and exhibit a very short ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ as well (see short red bar next to that LoS). As high-latitude clouds need to be nearby to be within the thin Galactic disk, the set of LoSs passing through them span a larger area of the high-latitude sky. We note that the scales or shape of this illustration are not intended to realistically match the Milky Way.

In the text

	Fig. 9 Inferred angular power spectra of the ${\overline{B_{\Vert }}}_{\text{gal}}$ (panel a) and DMgal (panel b) sky maps. The colors indicate the different runs from which the spectra where calculated (for details, see Sect. 3.3).
In the text

Fig. 10 Cutouts of several sky maps toward the HII region Sh 2-27. The images show a) ${\text{L}}_{{\text{DM}}^2/\text{EM}}$, b) ${\overline{B_{\Vert }}}_{gal}$, c) ϱEM/DM, and d) the foreground reduced B‖gal image from Raycheva et al. (2022), which is derived from diffuse polarized radio emission. The contours of the latter image are plotted over the first three images, with contour lines set at −2 µG (light blue) and −6 µG (dark blue). The elliptic boundary in d) indicates the projected boundaries of Sh2-27 assumed in Raycheva et al. (2022).

In the text

Fig. 11 Cutouts of several sky maps toward the Smith HVC. The images show a) ${\text{L}}_{{\text{DM}}^2/\text{EM}}$, b) ${\overline{B}}_{\Vert \text{gal }}$, c) ρEM/DM, and d) velocity-integrated HI observed by Justify the Green Bank Telescope (Lockman et al. 2008). Contours of the HI data are plotted over the first three images, with contour lines set at 30 K km s−1 (light violet) and 60 K km/s (dark violet).

In the text

Fig. 12 Scatter plots of pulsar observables vs. the respective inferred Galactic values. The coloring indicates the posterior mean of the wP parameter introduced in Eq. (19). Figs. (a) and (b) illustrate the RMp – RMgal correlation at high and low latitudes, respectively. Figs. (c) and (d) illustrate the correlation of the pulsar temporal broadening parameter, τsc , with DMgal and ϱEM/DM , respectively.

In the text

Fig. A.1 Illustrations of the priors used for the ${\langle B_{\Vert }\rangle }_{{\text{L}}_{\text{gal}}}$ , DMgal and ${\text{L}}_{{\text{DM}}^2/\text{EM}}$ sky models. The right side shows sky maps corresponding to four different samples drawn from the respective prior distributions. The left side shows histograms of the same prior samples, and additionally a line summarizing the distribution of values over 100 samples. The histograms were normalized to unity to ensure comparable scales.

In the text

	Fig. B.1 Synthetic datasets produced according to the procedure outlined in Sect. B. The plots show projections on the sky for the ideal (panel a) and realistic (panel b) cases of pulsar DM, as well as the RM (panel c) and EM data (panel d) sets.
In the text

	Fig. B.2 Ground truth and inference results for the synthetic data. The left column shows the ground truth for the B‖gal, log-DMgal and $\log {\text{-L}}_{{\text{DM}}^2/\text{EM}}$ skies. The middle and right column show the corresponding results for the ideal and realistic cases of pulsar DMs, respectively.
In the text

	Fig. C.1 Inference results for the Galactic Faraday and EM skies. Panel (a) shows the posterior mean for the Faraday sky, while panel (b) shows the posterior mean for the logarithmic EM sky.
In the text

	Fig. D.1 Inference results for the logarithmic Galactic DM sky of the secondary models introduced in Sect. 3.3. Panel (a) shows the posterior mean of the logarithmic DMgal sky constrained only by RM and DM data, and panel (b) the corresponding result constrained only by DM and EM data.
In the text

	Fig. D.2 Inference results of the secondary models introduced in Sect. 3.3. Panel (a) shows the posterior mean of the sky constrained only by RM and DM data, and panel (b) the filling factor sky constrained only by DM and EM data.
In the text