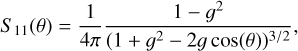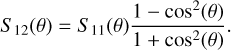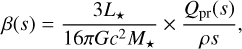| Issue |
A&A
Volume 674, June 2023
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202346097 | |
| Published online | 07 June 2023 | |
Apocenter pileup and arcs: A narrow dust ring around HD 129590★
1
Max Planck Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
e-mail: olofsson@mpia.de
2
Núcleo Milenio Formación Planetaria – NPF, Universidad de Valparaíso,
Av. Gran Bretaña 1111,
Valparaíso, Chile
3
Instituto de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso,
Av. Gran Bretaña 1111,
Playa Ancha, Valparaíso, Chile
4
LESIA – Observatoire de Paris, UPMC Univ. Paris 06, Univ. Paris-Diderot,
Paris, France
5
European Southern Observatory,
Karl-Schwarzschild-Strasse 2,
85748
Garching bei München, Germany
6
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
7
European Southern Observatory,
Alonso de Cordova 3107, Casilla
19001,
Vitacura, Santiago, Chile
Received:
7
February
2023
Accepted:
12
April
2023
Context. Observations of debris disks have significantly improved over the past decades, both in terms of sensitivity and spatial resolution. At near-infrared wavelengths, new observing strategies and post-processing algorithms allow us to drastically improve the final images and reveal faint structures in the disks. These structures inform us about the properties and spatial distribution of the small dust particles.
Aims. We present new H-band observations of the disk around the solar-type star HD 129590, which display an intriguing arc-like structure in total intensity observations but not in total polarimetry, and we propose an explanation for the origin of this arc.
Methods. Assuming geometric parameters for the birth ring of planetesimals, our model provides the positions of millions of particles of different sizes to compute scattered light images. The code can either produce images over the full size distribution or over several smaller intervals of grain sizes.
Results. We demonstrate that if the grain size distribution is truncated or strongly peaks at a size larger than the radiation pressure blow-out size, we are able to produce an arc quite similar to the one detected in the observations. If the birth ring is radially narrow, given that particles of a given size have similar eccentricities, they will have their apocenters at the same distance from the star. Since this is where the particles spend most of their time, an “apocenter pileup” occurs that can look like a ring. Due to more efficient forward scattering, this arc only appears in total intensity observations and remains undetected in polarimetric data, which is in good agreement with our observations.
Conclusions. For the secondary ring to be detected, sharp variations either in the grain size distribution or for the scattering efficiencies Qsca (or a combination of both) are required. We show that a wavy size distribution and a size-dependent phase function can strengthen the apocenter pileup. Overall, such arcs are rarely detected in other systems, which can mainly be explained by the fact that most parent belts are usually broad.
Key words: circumstellar matter / instrumentation: high angular resolution
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Since the first detection of circumstellar dust around a main sequence star other than the Sun (Aumann et al. 1984), observations of debris disks have kept on improving. Starting from unresolved far-IR photometry, we now have access to optical and near-IR extreme adaptive optics instruments, such as the Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE, Beuzit et al. 2019), the Gemini Planet Imager (Macintosh et al. 2014), or the Subaru Coronagraphic Extreme Adaptive Optics system (Jovanovic et al. 2015), as well as (sub)millimeter interferometric high angular resolution observations with the Atacama Large Millimeter/submillimeter Array (ALMA). These instruments and facilities offer an angular resolution of a few tens of milli-arcsec (mas), allowing us to spatially resolve debris disks with exquisite detail, revealing the birth ring where planetesimals collide and release the small dust particles that we can observe.
Thanks to the high angular resolution of near-IR scattered light observations, we have started to detect faint substructures ranging from from multiple belts (HD 131835, Feldt et al. 2017, and HD 120326, Bonnefoy et al. 2017), spiral arms, clumps, and rings (TWA 7, Olofsson et al. 2018; Ren et al. 2021) to large-scale, extended swept-back wings or halos (HD 61005 and HD 32297, Schneider et al. 2014, and HR 4796, Schneider et al. 2018). In this paper, we investigate what can be learned from the detection of some of these substructures in the case of HD129590.
A G3V star, HD 129590 is located at 136.32 ± 0.44 pc (Gaia Collaboration 2016, 2021). It is a member of the Upper Centaurus Lupus Sco-Cen region (de Zeeuw et al. 1999; Chen et al. 2011). It hosts a bright debris disk (fractional luminosity ƒdisk ~ 5 × 10−3; Jang-Condell et al. 2015) that was first spatially resolved at near-IR wavelengths, in total intensity, by Matthews et al. (2017). The disk is highly inclined (i ~ 75°) with a radius of 60–70 au (58 and 67.7 au, correcting for the previous estimate of the distance of 141 pc). Olofsson et al. (2022b) presented polarimetric observations of the disk, and found a slightly larger inclination (i ~ 82°) and a smaller radius (47.6 au). From ALMA observations, Kral et al. (2020) also reported the detection of CO gas in the system (~ 10−4 M⊕), making it the first debris disk around a solar-type star to harbor cold gas.
In this paper, we present new observations obtained with the SPHERE instrument using the star-hopping method (Wahhaj et al. 2021). The observations were processed using recent postprocessing algorithms, allowing us to retrieve faint structures in the total intensity image. The aim of this paper is not to perform detailed modeling of the observations but rather discuss what we can learn about the properties of the disk from the detection of such structures.
2 Observations and data reduction
The data set used in this study was obtained with the SPHERE IRDIS instrument (Dohlen et al. 2008) using the dual-beam polarimetric imaging mode (DPI; de Boer et al. 2020, van Holstein et al. 2020) in pupil tracking (van Holstein et al. 2017) in the H band (λc = 1.62 µm). The observations were performed making use of the star-hopping mode of the instrument (Wahhaj et al. 2021) where the instrument hops back and forth between the science target and a reference star. The motivation was to build a reference coronagraphic image from the reference calibrator star without any circumstellar material to be subtracted from the science cube in order to reveal faint signals in total intensity in the immediate vicinity of the star.
2.1 SPHERE total intensity images
Most routinely when studying debris disks, the pupil-stabilized observations are processed using angular differential imaging (Marois et al. 2006) with a principal component analysis (PCA), however, self-subtraction can significantly alter parts of the disk (especially along the projected semi-minor axis, Milli et al. 2012). Self-subtraction can be mitigated using approaches such as forward modeling (e.g., Olofsson et al. 2016; Chen et al. 2020; Mazoyer et al. 2020); nonetheless, it remains a model-dependent approach. In the past years, several algorithms have become available for the processing of observations without having to rely on a model of the disk and lowering the impact of self-subtraction, such as GreeDS (Pairet et al. 2018), REXPACO (Flasseur et al. 2021), MAYONNAISE (Pairet et al. 2021), and mustard (Juillard et al. 2022), or performing data imputation with sequential non-negative matrix factorization (DI-sNMF, Ren et al. 2020). These post-processing algorithms show promising results and allow us to recover the signal from the disk without suffering from most of the drawbacks of PCA.
In this study, we processed our total intensity observations using the DI-sNMF algorithm, making use of reference star differential imaging (RDI). In programs 105.20GP.001 and 109.237K.001, we observed four reference stars, HD 117255, HD 129280, HD 158018, and HD 191131, with the same observing mode as for HD 129590. After reducing the data using the IRDAP1 package described in van Holstein et al. (2020, version 1.3.4), we obtained a master calibrator cube of 222 reference coronagraphic images that could be used to perform RDI. Since the observations have different integration times, each frame was normalized by its corresponding integration time prior to constructing the cube. From this cube, we used the DI-sNMF package2 to construct the NMF components (a nonorthogonal, non-negative basis built from reference images; see Ren et al. 2018). These components were then used on the science data cube (32 individual frames), and a numerical mask of 1′′ in radius, centered on the star, was applied to exclude the disk and perform the data imputation. We used 50, 75, 100, and 200 components for the reduction, and the differences between the final reductions were minute. We therefore used the reduction with 75 components. The left and top-right panels of Fig. 1 show the DI-sNMF and PCA3 reduction, respectively, illustrating the significant differences between the two reductions. Not only was there almost no negative signal in the DI-sNMF reduction, but the flux of the projected semi-minor axis was much better recovered compared to the PCA reduction, where it was completely lost to self-subtraction effects. For the rest of this study, when referring to the total intensity observations, this means the DI-sNMF reduction.
2.2 Linear polarimetric images
To obtain the images in linearly polarized light, we used the same reduction as the one presented in Olofsson et al. (2022b), for which we had also used the IRDAP package. The reduction yielded the Qϕ and Uϕ images. The former image contained the signal from the disk, and the latter could be used as a proxy for the uncertainties since it does not contain astrophysical signals (assuming single scattering by particles). The Qϕ image is shown in the bottom-right panel of Fig. 1.
2.3 Detection of an arc in total intensity
Figure 1 shows some interesting differences between the total and polarized intensity observations. The Qϕ image is rather straightforward to explain. The birth ring, where planetesimals collide with each other, is well resolved, and the disk extends along its major axis into a halo. This halo traces the small dust particles sent on eccentric orbits due to radiation pressure (or a combination of radiation pressure and gas drag; Kral et al. 2020; Olofsson et al. 2022b). In polarimetric observations, forward scattering is not as strong as it is in total intensity observations. The polarized phase function either peaks (or plateaus) around scattering angles4 in the range of 60–90° or slowly decreases with increasing scattering angles (Olofsson et al. 2022b). Combined with an increase in column density along the major axis due to the inclination of the disk (Olofsson et al. 2020), this renders the major axis of the disk brighter than its minor axis. In the bottom-right panel of Fig. 1, we also show the location of the birth ring reported in Olofsson et al. (2022b).
The total intensity observations display different structures that are not visible in the Qϕ image. The birth ring was also detected for a wide range of scattering angles, as we could even detect the back side of the disk (the front side being located toward the north-northeast). We could also see an “arc-like” structure that seemed to be parallel to the direction of the major axis but slightly offset toward the north, begging the question of its origin. In the figure, we also highlight the location of the arc.
We note that the arc also seems to be detected in the reduction presented in Matthews et al. (2017, see their Fig. 4), but it was not discussed. To assess whether the detection of this arc is an artifact of the DI-sNMF reduction, Fig. A.1 shows alternative reductions of the science data cube using other algorithms (GreeDS and MAYONNAISE), in which similar structures are recovered.
 |
Fig. 1 SPHERE-IRDIS observations of the disk around HD 129590. Left panel: DI-sNMF total intensity reduction. The detection of the birth ring and the presence of a faint arc are highlighted by two arrows in the left panel. The inset in the left panel also shows the DI-sNMF reduction with the birth ring (best-fit from Olofsson et al. 2022b) and the arc highlighted. Top-right panel: PCA total intensity reduction. Bottom-right panel: Qϕ polarized intensity reduction. The location of the birth ring is shown in the Qϕ image as a solid black line. For each image, the central mask has a radius of 0.125′′, and the color scale is linear. North is up, east is left, and the pixel scale is of 12.26 mas. |
3 A possible explanation: Apocenter pileup
3.1 A secondary ring
One possible explanation for the morphology of the disk as seen in the total intensity observations would be the presence of an outer disk (as discussed in Bonnefoy et al. 2017 for HD 120326; see also Sect. 4.2). Due to projection effects for an inclined system, the outer belt could appear as slightly overlapping the inner one, therefore appearing as an arc.
To fit the spectral energy distribution, Chen et al. (2014) required two Planck functions at different temperatures, but both Ballering et al. (2013) and Jang-Condell et al. (2015) could reproduce it using only one temperature (see discussion in Matthews et al. 2017). Furthermore, the polarimetric observations are of good quality and the “inner” disk is well detected, while there is no indication for the presence of an outer disk in this data set. Ultimately, we would need high angular resolution observations with ALMA (in Kral et al. 2020, the beam size was larger than 1′′) to confirm that there is a single belt around HD 129590. The scenario of two belts seems unlikely, as it would require that the dust particles in the outer ring have a near-zero degree of polarization so that they scatter enough stellar light to be detected in total intensity while remaining undetected in polarized light. Given how bright the disk is in the Qϕ image, this would imply drastically different dust properties for the inner and outer belts. For the rest of this study, we assume that there is only one birth ring around HD 129590 and try to explore alternative explanations for the presence of the arc-like structure.
3.2 Radiation pressure and radial size segregation
As previously mentioned, the phase functions in total and polarized intensity observations are expected to be quite different. In this subsection, we therefore explore if the phase function can explain why we detect an arc-like structure in the total intensity observations even though it is not seen in the polarimetric data. We used the same code as the one described in Olofsson et al. (2022a)5, which can compute scattered light images for different grain sizes. We refer the interested reader to the original paper for additional details, but in short, the code launches millions of particles that are parametrized by their β ratio (the ratio between radiation pressure and gravitational forces, ∝ 1/s, where s is the particle size). All the particles are initially released from the birth ring, which follows a normal distribution centered at a0 with a standard deviation δa, and the code computes the updated orbital parameters for each particle, including the effect of radiation pressure. Large dust particles (small β) will remain in the vicinity of the birth ring, while small particles (large β) will be set on highly eccentric orbits. We only considered grains that remained gravitationally bound to the star and did not include unbound grains (β ≥ 0.5 if initially released from a circular orbit). The code accounts for the illumination factor (∝1/r2), the geometric cross section of the particles (∝1/β2 since β ∝ 1/s), the size distribution (dn(β) ∝ β1.5dβ, equivalent to dn(s) ∝ s−3.5ds, Dohnanyi 1969), and a “correction factor” α. The last term is necessary because particles set on eccentric orbits will travel in regions of very low density, and therefore their lifetime can be significantly increased (see Strubbe & Chiang 2006; Thébault & Wu 2008).
The code can also take a phase function as an input, which can follow the Henyey-Greenstein (HG) approximation (Henyey & Greenstein 1941). In total intensity, the phase function takes the following form
where ɡ is the asymmetry parameter (−1 < ɡ < 1) and θ the scattering angle. In polarized intensity, the polarized phase function takes the form of
For all the particles, the code draws values for β between βnin and βmax (usually 0.01 and 0.49), but it is possible to bin the β values in different ng intervals. Figure 2 shows different images for five different β intervals (with ng = 12) in total and polarized intensity (top and bottom panels, respectively). The parameters for the birth ring are taken from Olofsson et al. (2022b), with the inclination i = 82°, the position angle ϕ = −60.6°, the semi-major axis a0 = 0.35′′ (47.7 au at a distance of 136.32 pc), and the width of the birth ring δa = 0.025′′ (3.4 au), and we used a value of 0.7 for ɡ in both the total and polarized intensities. While Matthews et al. (2017) found a value for the asymmetry parameter ɡ closer to 0.4–0.5, our choice for ɡ = 0.7 is motivated by the analysis presented in Sect. 3.4. For comparison, Fig.B.1 shows images similar to those presented in Fig. 2 for ɡ = 0.5. For the vertical structure of the disk, we assumed a normal distribution with a constant aspect ratio and an opening angle of 0.02 radians, based on the results of Olofsson et al. (2022b), where they found the disk to be vertically thin.
For β = 0.02 (leftmost panels of Fig. 2), the images trace the birth ring, as the large particles do not experience strong radiation pressure. Because of forward scattering, the semi-minor axis of the disk appeared bright in the total intensity observation, while the major axis would be best traced in polarized light. As β increased (up to β ~ 0.35), we started to see the extended halo become more prominent in the images as a result of the particles’ increased apocenter distances. In polarized intensity, because of the shape of the phase function, this halo extended in the continuity of the major axis of the disk. On top of the phase function itself, as mentioned previously, the major axis was also brighter simply because of the projection effects from the high inclination of the disk. We probed a larger column density along the major axis compared to the minor axis of the disk. However, we observed that the situation was quite different in total intensity. Due to the stronger forward scattering, the front side of the minor axis became brighter than the major axis, and for the images with β = 0.27 and 0.35, an arc quite similar to the one seen in the observations became noticeable. Interestingly, for β = 0.43 (and larger), the halo became so extended that it appeared relatively faint, and we mostly, once again, saw the birth ring of the disk.
The origin of the arc only seen in total intensity observations is driven by two main “parameters”. The first one is a natural consequence of the way the images were computed. By selecting a narrow range of β values, we only accounted for a population of particles that were released from the same distance from the star (~a0 ± δa; see next paragraph) and had more or less the same eccentricity (e ~ β/(1 – β)). This meant that all these particles would have the same apocenter distance (but with arguments of pericenter uniformly distributed between [0,2π]). Since the particles spent most of their time near that location, it resulted in a pileup of particles (which we refer to as the “apocenter pileup”).
If we considered the full size distribution (and not one interval of β values), the sum of all the apocenter pileups would result in a halo with a surface brightness that naturally follows a power-law (e.g., Thébault & Wu 2008). Figure 3 shows images integrated over the full size distribution, between βmin and βmax, in total and polarized intensity (top and bottom panels, respectively). The arc-like structure has disappeared, and we retrieved a continuous halo beyond the birth ring (best seen with the square root scaling for both panels). We note that it is also important to keep in mind that in the modeling approach, we assumed that all the grain sizes have scattering efficiencies Qsca equal to unity, which is a simplification that we further investigate in Sect. 3.3. Even if the surface density (or optical depth) profile follows a power-law, variations in Qsca might indeed affect the resulting appearance of the disk in scattered light observations.
The second “parameter” related to the origin of the arc can inform us about the intrinsic properties of the birth ring and is related to the radial width of the birth ring. For the apocenter pileup to be bright enough to be detected, the range of apocenters for a population of particles with comparable β needs to be narrow. The range of the apocenters is positively correlated with the width of the birth ring. Therefore, the detection of an arc strongly suggests a very narrow birth ring where the collisions are taking place (justifying why we used δa = 0.025′′ in Fig. 2), possibly combined with a variation of the dust properties. But overall, if there is no secondary dust belt, the narrowness of the birth ring is a prerequisite for the detection of an arc.
 |
Fig. 2 Simulated disk images for total intensity (top panels) and polarized intensity (bottom panels) for different narrow intervals of β, and the average value of β is reported in each panel. The value of the asymmetry parameter ɡ is set to 0.7 for all images. The scaling is linear and adjusted to the 99.9 percent for all frames. The images are convolved with a 2D Gaussian with a standard deviation of two pixels. |
 |
Fig. 3 Total intensity and polarimetry images integrated over the full size distribution between βmin and βmax with a square root scaling. |
3.3 Scattering efficiencies
As mentioned previously, the scattering efficiencies Qsca can affect the surface brightness profile of the disk. Particles of some sizes scatter the stellar light more efficiently than others. To have a first order estimate of this effect, we computed both the β ratio and the Qsca values for a given dust composition as a function of the grain size, and the results are displayed in Fig. 4. To compute those values, we used the Distribution of Hollow Spheres model (DHS, Min et al. 2005) with a maximum filling factor of fmax = 0.8 and with the “DIANA” composition (pyroxene and carbon with a mass ratio of 87% and 13%, respectively; a porosity of 25%, Woitke et al. 2016; and optical constants from Dorschner et al. 1995 and Zubko et al. 1996, respectively), using the optool6 package (Dominik et al. 2021). As explained in Woitke et al. (2016) and references therein, this dust mixture is expected to be well representative of particles in circumstellar disks.
The β ratio was computed following Burns et al. (1979) as
where M⋆ and L⋆ are the stellar mass and luminosity (1.3 M⊙ and 3.1 L⊙, respectively, taken from Kral et al. 2020), G is the gravitational constant, c is the speed of light, and ρ is the density of the dust particles. The radiation pressure efficiency is shown as Qpr(s) and is equal to Qext(s, λ) – ɡsca(s) × Qsca(s, λ) averaged over the stellar spectrum. The Qext and Qsca are the extinction and scattering efficiencies and ɡsca the asymmetry parameter, all of which were computed using optool.
While both β and Qsca depend on the composition and porosity of the particles, for a “typical” circumstellar composition (the DIANA standard opacities), Fig. 4 shows an interesting behavior. The blow-out size, sblow–out, above which the grains remain gravitationally bound to the star, is about 1.2 µm, and coincidentally this characteristic size also corresponds to a maximum of the scattering efficiency. Moreover, the Qsca values decreased as s increased before reaching a plateau for sizes of about ~ 10 µm. With all other aspects already considered in the code and discussed above (i.e., size distribution, cross section of the grains, stellar illumination, extended lifetime outside of the birth ring), the contribution to the total flux of the smallest bound particles was enhanced by an additional factor of approximately two, compared to larger particles, solely because of the Qsca values.
As discussed at the end of the last section, there are two “parameters” that can lead to the detection of an arc-like structure. The first one is to have a population of particles with a narrow range of β values. If the size distribution is too wide (see Fig. 3 with the full size distribution), then the arc disappears, but adding the dependency of Qsca with s in the mix might change this result. Even for a wide-size distribution, the important Qsca(s) variations could indeed increase the contribution to the flux of a relatively narrow domain of particle sizes close to sblow–out. There is here, however, a competition between the Qsca values and the illumination factor (∝ 1/r2). Indeed, the particles that have large Qsca values are also the ones with larger β values (as long as particles are bound, that is, β < 0.5) and are therefore far away from the star and receive less stellar light. For example, we did not see an arc for the particles close to the blow-out size (top-right panel of Fig. 2) even though they had the largest Qsca values (Fig. 4).
Figure 5 shows images in total intensity (see Fig. B.2 for the same images in polarized intensity). The top panel is the same as for Fig. 3, assuming a size distribution in dn(s) ∝ s−3 5ds and Qsca values equal to unity. In the middle panel, we took into account the variation of Qsca as a function of the grain size s (Fig. 4), and the bottom panel is further discussed in Sect. 3.5. The images have a square root scaling to better highlight the faint halo, and overall the differences between the top and middle images are marginal. The variation in Qsca as a function of s does not seem to be sufficient to explain the presence of an arc.
 |
Fig. 4 Ratio of β and Qsca scattering efficiencies (different y axis) as a function of the grain size. The vertical line denotes the blow-out size for which β = 0.5 (horizontal line). |
 |
Fig. 5 Total intensity images integrated over the full size distribution between βmin and βmax The different panels show the differences when accounting for the wavy size distribution or the variation of Qsca as a function of s. The images are shown with a square root scaling to better highlight the regions outside the birth ring. |
3.4 A size-dependent phase function
In addition to the previous considerations, there is also a geometrical issue, which is that the arc seen in our simulated images appears slightly more “curved” compared to the one seen in the observations (e.g., third or fourth panels of Fig. 2). This is because, assuming the birth ring is circular (Olofsson et al. 2022b could reproduce the Qϕ observations without needing an eccentric disk), the apocenter pileup for a narrow range of β will also be circular. For each panel of Fig. 2, we only considered narrow intervals of β values and the same phase function (ɡ = 0.7). But the phase function does depend on the grain size (and as a consequence of radiation pressure, on the stellar distance). In total intensity, grains much smaller than the wavelength should in principle display isotropic scattering, while grains larger or comparable to the wavelength should scatter in the forward direction more efficiently. Coupled with the efficient-size segregation caused by radiation pressure, the integrated phase function at different distances from the star should vary, which could in the end alter the shape of the arc.
There is in fact a way to check if our observations point toward a phase function that varies with stellar distance. This can be done by computing, at different radial distances, the brightness profile as a function of the scattering angle in the midplane (assuming the disk is vertically thin7). This is done in concentric annuii accounting for the inclination and position angle of the disk (hence deprojected stellocentric distances). We binned the scattering angles in 30 bins between 0° and 180°, and for each bin we selected, the pixels that had a midplane scattering angle within the range of the considered bin. We then computed the mean value of the selected pixels. Figure 6 shows the extracted profiles for seven annuii with a width of 0.1′′ between 0.3′′ and 1′′ (deprojected distances). Since we masked the innermost regions of the image (0.125′′), the profiles for the first three annuii cover a smaller range of scattering angles. In the top panel, we added an offset to the profiles for clarity, and the horizontal lines show the zero point, while the bottom panel shows the profiles without the offset for a direct comparison between them. Furthermore, for each annulus, we used lmfit (Newville et al. 2021) to find the HG-phase function (Eq.(1)) with the g value that best fits the profile. The best-fitting values are reported in the legend of Fig. 6, and the best HG fits are shown with dimmer lines underneath the extracted profiles in the top panel. In the legend, we also provide an estimate of the β values of the particles that dominate the geometrical cross section for each range of distance. To compute the β values, we assumed that between the deprojected distances r1 and r2 (e.g., 0.7 and 0.8′′) are particles that have their apocenter at this distance from the star, while their pericenter lies in the birth ring (r0 = 0.35′′, Olofsson et al. 2022b). We computed  and derived the eccentricity
and derived the eccentricity 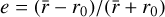 , from which we derived the “typical”β value as e/(1 + e). This was only done to provide a rough estimate of the typical grain size, and the β values were not used when extracting the profiles.
, from which we derived the “typical”β value as e/(1 + e). This was only done to provide a rough estimate of the typical grain size, and the β values were not used when extracting the profiles.
In Fig. 6, we could see that there may be some back-scattering for all seven profiles that the Henyey-Greenstein functions fail to capture (since we used only one value for ɡ) for scattering angles larger than approximately 150°. This back-scattering could be real, but it could also be due to an improper subtraction of the reference images, leaving some residual flux near the center of the image. We also note that the HG fits to the first two brightness profiles ([0.3, 0.4″] and [0.4, 0.5″]) do not reproduce their shape very well, though the fits are quite decent for the other profiles (beyond ~0.5–0.6″). Interestingly, we could see the value of ɡ increase the farther away we moved from the birth ring, and this result is quite counterintuitive. We would expect small particles (large β) to scatter isotropically, leading to lower values of ɡ, while we observed the opposite trend, with ɡ reaching a value of 0.8 ± 0.01 for the largest β values. The difference with the values of ɡ reported in Matthews et al. (2017, ɡ = 0.42–0.52) can be explained by the better recovery of the semi-minor axis of the disk in the DI-sNMF reduction compared to the PCA reduction.
Even though this seems counterintuitive at first, things are not that straightforward. It is important to keep in mind that our assumption of a single grain size at a given distance in the halo is not fully true. At a given distance outside the birth ring, we still probed for a distribution of sizes, as the smallest bound grains would contribute to the flux of all the concentric annuli, not only in the outermost annulus where their apocenter is. On top of that, for an inclination of i = 82°, we probed scattering angles in the range [90° − i, 90° + i], meaning that we would miss the very small (and large) scattering angles (the missing angles are marked by the gray-shaded areas in Fig. 6). For grains as large as ~5 µm, the strong forward scattering peak can fall in this “blind” range (see Mulders et al. 2013). Therefore, by missing the forward scattering peak, the phase function of large grains might in fact appear almost isotropic in the range of angles we probed8. Our results seem to indicate that the smallest dust grains that our observations are sensitive to have a phase function with ɡ ~ 0.8 (bottom profile in Fig. 6, between 0.9 and 1″). As we moved closer to the birth ring, larger grains also contributed to the flux, and these particles might have an isotropic “effective” phase function, as we are missing the strong forward scattering peak. This results in an integrated phase function with lower ɡ values because the contribution of the larger grains continues to effectively add flux at all scattering angles.
Overall, this discussion remains to be further tested. There are some aspects that our procedure does not take into account, such as the vertical scale height (Olofsson et al. 2020), the effects of the convolution and of the inclination of the disk when extracting the profiles (elliptic apertures, Milli et al. 2017), and using more realistic phase functions than the HG approximation (Eq. (1)). Nonetheless, variations of the phase function as a function of the size, hence β and hence radial distance, is something that could possibly explain the shape of the arc seen in the observations. Indeed, as can be seen in Fig. 6, for scattering angles in the range 25°–50°, the annuli become relatively brighter as r decreases (bottom to top). This widens the wings along the minor axis of the disk, thus altering the shape of the arc. Furthermore, as the quality of the observations and post-processing algorithms continue to improve, using a single-phase function for the whole disk (birth ring and halo) might become a limitation when modeling the scattered or polarized light observations. The change in the size distribution as we venture away from the birth ring might bias our characterization of the phase functions of young debris disks.
 |
Fig. 6 Surface brightness as a function of the scattering angle extracted in concentric annulii, accounting for the inclination and position angle of the disk, with increasing deprojected stellocentric distances r (in arc-sec). For clarity, the profiles have been offset and the horizontal lines show the zero point in the top panel, while no offset has been included for the bottom panel to best compare the different profiles. The fainter lines in the top panel show the best-fit with an HG-phase function (the ɡ values are reported in the legend). The gray-shaded areas show the scattering angles that are not accessible to us for an inclination of 82°. |
3.5 A wavy size distribution
For the apocenter pileup to produce a detectable arc, we need to have a rather sharp variation for one of the following two variables. We either need a strong peak in the size distribution, to “isolate” a particular particle size, or an equally strong peak in the scattering efficiencies (resulting in a similar “isolation” of a given grain size by making all the other sizes dimmer). Regarding the latter explanation, it is challenging to think that there could be a drop in Qsca sharper than the one displayed in Fig. 4.
A result that might help explain the apocenter pileup was presented in Thébault & Augereau (2007), and the authors demonstrated that the size distribution can display some wavy structures. The origin of this waviness comes from the fact that grains with a size s can efficiently destroy particles with a size s + δs. Because of the radiation pressure, there is a lack of grains with sizes s ≲ sblow–out, leading to an overabundance of particles with s ≳ sblow–out, which can efficiently destroy slightly larger grains. As time passes, this pattern of over- or under-abundance propagates throughout the whole size distribution. However, the authors showed that the resulting pattern is rather smooth, and the first “peak” can extend in the range ~5–10 µm in their simulations. Interestingly, their resulting mass distribution shows a very steep increase right before the first peak, which is not located at sblow–out but at slightly larger sizes (speak ~ 1.5 × sblow–out). Assuming β ∝ 1/s and that βblow–out = 0.5, we find that βpeak ~ 0.33. Going back to Fig. 2, the first peak of the wavy size distribution would then correspond to the second-to-last upper panel (with β ~ 0.35). The contribution of grains with larger β values would be severely diminished (rightmost upper panel) because of the wavy distribution, which is the ideal configuration for the arc to naturally appear in the observations. Particles with smaller β can still remain in the system, but their apocenter will never reach as far out, and they therefore would not be able to dilute the apocenter pileup. In other words, this could work if the size distribution is effectively cutoff at a slightly larger size than the blow-out size, possibly combined with larger Qsca values for smaller particles.
The bottom panel of Fig. 5 shows the image in total intensity when also accounting for the wavy size distribution (following Eq. (5) from Thébault & Augereau 2007). The main difference between the three images is that the halo seems to be slightly brighter when including the wavy size distribution along with the scattering efficiencies and seems to be slightly offset compared to the projected major axis of the disk. However, the square root scaling is necessary to reveal the halo, which remains faint. This could be due to the choice of the dust composition and the variation of Qsca that is not sufficient to make the halo brighter, or this could be due to the shape of the wavy size distribution. In Fig. 4 the peak of Qsca corresponds to s ~ sblow–out, but if a different composition were to shift the peak toward slightly larger sizes (e.g., close to β ~ 0.35), it might help increase the contribution of the arc. Furthermore, Eq. (5) from Thébault & Augereau (2007) is meant for radially broader disks and might not be directly applicable for narrower birth rings. To conclude on this exercise, it goes in the right direction even though the magnitude of the effect might not be sufficient to reproduce the observations. Another additional effect that might help strengthen the signal from the arc is to also include the variation of the phase function with the grain size. Unfortunately, this cannot be easily tested since we can hardly quantify this variation. Figure 6 might seem to be a good starting point, but the fact that the derived values of ɡ are not for a single grain size must be kept in mind. As mentioned before, for each concentric annuli there is a distribution of grain sizes contributing to the surface brightness, and we cannot easily determine the relationship between ɡ and β (to determine ɡ(s)).
Overall, explaining why we would detect only a narrow range of particle sizes (either because of the underlying size distribution or because of the optical properties) remains quite a significant challenge. But the fact remains that the total and polarized intensity observations of HD 129590 show different structures. Furthermore, the fact that the arc is actually seen in the reduction of Matthews et al. (2017, different team, data set, and reduction process) bring confidence that the arc is indeed real and needs to be explained.
3.6 The width of the birth ring
As mentioned in Sect. 3.2, for the apocenter pileup to produce an arc, the birth ring must be narrow enough so that the apocenters of particles of comparable sizes are not too radially diluted. It can therefore be an indirect way to indicate that the parent plan-etesimals are indeed arranged in a ring with a semi-major axis that has a small range. A clear follow-up observation would be to image HD 129590 with ALMA at a high angular resolution (the beam size in the observations presented in Kral et al. 2020 was 1.61 × 1.16″) and assess whether the birth ring is indeed narrow or radially extended.
4 Perspectives and discussion
4.1 Total intensity versus polarimetry
The results presented in this paper add to the already known differences between total and polarized intensity observations of debris disks. Simply because of the different shapes of the phase function, total intensity observations usually trace the projected minor axis of the disks best, while their major axis is usually best revealed in polarimetric observations. But as demonstrated above, the differences between the total and polarized intensities can be even more profound and can in fact strongly bias our interpretation of the structure of the disk. A disk can appear as a single belt in the polarimetry, and an additional faint arc might appear in the total intensity data. We showed that this arc should not always be interpreted as the presence of a secondary belt, as it can instead be a mirage caused by the combination of radiation pressure and a more forward scattering phase function.
As a side note, the presence of the arc in the total intensity image might slightly bias the determination of the inclination of the disk. Matthews et al. (2017) determined an inclination of approximately 75° from their total intensity reduction, while Olofsson et al. (2022b) obtained an inclination of i ~ 82° when modeling the polarized intensity observations. In total intensity, as the arc shifts the photocenter along the direction of the minor axis of the disk, it can make the disk appear less inclined than it really is. For these reasons, polarized observations allow us to more reliably constrain the actual morphology and geometry of debris disks (on top of being less affected by post-processing algorithms).
4.2 Arcs in other debris disks
If our interpretation for the detection of the arc-like structure holds for HD 129590, one may wonder why such arcs are not routinely detected in other debris disks. As mentioned previously, there is at least one prerequisite: The birth ring must be quite narrow so that the pileup at the apocenter is not too spread out. However, as mentioned in Marino (2022), results from the REASONS survey (Matrà et al., in prep.) suggest that debris disks are in general quite extended radially, with a median fractional width (∆r/r) of about 0.74, much wider than the Kuiper belt of the solar system for instance (~0.27). This would suggest that the disk around HD 129590 is to some extent different than most of the other debris disks. This could explain why such structures are not routinely detected.
But the case of HD 120326 (HIP 67497) is an interesting comparison point. Bonnefoy et al. (2017) reported the detection of an inclined disk (i ~ 80°) as well as an arc in the SPHERE total intensity observations and investigated several scenarios. They first modeled the inner belt only (corresponding to the birth ring in our case), assuming steep power-law distributions for the volumetric density, αin = 10 and αout = −5, indicative of a rather narrow birth ring located at 58.6 au. They then tested two models to be added to this inner belt: an extended halo and another birth ring (with a reference radius different from the one of the first belt). Based on the residuals, they concluded that the latter scenario was more likely, and for this secondary belt, they found a radius of 130 au and an outer slope in αout = −8, a sharp outer edge for the secondary ring. From their images, the secondary ring appears to be quite far from the innermost one, and a “gap” between the two can be observed. Nonetheless, Olofsson et al. (2022b) presented polarimetric observations of the same disk, and no secondary ring was detected in the observations, suggesting that HD 120326 could well be a twin (or maybe a relative) of HD 129590.
A possible counterexample is HR 4796. It has a narrow and inclined birth ring but no apparent secondary ring or arc. The disk has been intensively monitored at near-IR wavelengths, both in total and polarized intensity, and no arc in the vicinity of the main ring has ever been reported. But Schneider et al. (2018) presented the detection of “extensive exo-ring dust material” from Hubble Space Telescope observations and reported that this exo-ring is located much farther away from the birth ring.
For the sake of the argument, we assumed that for the three objects (HD 129590, HD 120326, and HR 4796), the arcs can be solely explained by the apocenter pileup. One of the main differences between these three stars is that their spectral types are G3, F0, and A0, respectively. In Sect. 3.5, we discussed the possible impact of a wavy size distribution as described in Thébault & Augereau (2007). However, the authors investigated the effect that the central stellar mass could have on their results and found the differences to be negligible. Their Fig. 7 shows that the size distribution simply shifts depending on the value of sblow–out, but the shape of the peak and of the steep increase before it seem to remain similar. It would therefore be challenging to explain why the arc around HR 4796 is located so far away from the birth ring.
5 Summary
In this paper, we reported on the detection of an arc-like structure in the disk around HD 129590. This arc is only detected in total intensity and not in the polarimetric data. After discussing why it is unlikely related to a secondary ring, we proposed a possible mechanism that could be responsible for its detection. A promising candidate for such a mechanism would be the apoc-enter pileup in which we detected the apocenter of particles of a given size. While the faint arc remains challenging to explain, it could be due to some truncation of the size distribution at β values smaller than the expected cutoff size of β ~ 0.5 (otherwise the apocenters are too far away for the pileup to be detected). We hypothesize this could be the consequence of a wavy size distribution possibly combined with the dependence of Qabs as a function of the particle size s.
A requirement for the apocenter pileup to be detected is that the birth ring needs to be radially narrow so that the apocen-ters are not too diluted. Given that most disks have rather broad birth rings, this could explain why such structures are not routinely detected, but the disks around HD 129590 and HD120326 (and possibly HR 4796) are interesting candidates to further investigate this effect. Future high angular resolution ALMA observations would help confirm the width of the planetesimal belt of the disk around HD 129590.
Acknowledgements
We thank the anonymous referee for a constructive and helpful report, that helped strengthen the results of this paper. J.O., A.B., B.M.-O., and N.G. acknowledge support by ANID, – Millennium Science Initiative Program – NCN19_171. K. M. is funded by the European Union (ERC, WANDA, 101039452). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. SPHERE is an instrument designed and built by a consortium consisting of IPAG (Grenoble, France), MPIA (Heidelberg, Germany), LAM (Marseille, France), LESIA (Paris, France), Laboratoire Lagrange (Nice, France), INAF – Osservatorio di Padova (Italy), Observatoire de Genève (Switzerland), ETH Zurich (Switzerland), NOVA (The Netherlands), ONERA (France) and ASTRON (The Netherlands) in collaboration with ESO. SPHERE was funded by ESO, with additional contributions from CNRS (France), MPIA (Germany), INAF (Italy), FINES (Switzerland) and NOVA (The Netherlands). SPHERE also received funding from the European Commission Sixth and Seventh Framework Programmes as part of the Optical Infrared Coordination Network for Astronomy (OPTICON) under grant number RII3-Ct-2004-001566 for FP6 (2004-2008), grant number 226604 for FP7 (2009–2012) and grant number 312430 for FP7 (2013-2016). We also acknowledge financial support from the Programme National de Planétologie (PNP) and the Programme National de Physique Stellaire (PNPS) of CNRS-INSU in France. This work has also been supported by a grant from the French Labex OSUG@2020 (Investissements d’avenir – ANR10 LABX56). The project is supported by CNRS, by the Agence Nationale de la Recherche (ANR-14-CE33-0018). It has also been carried out within the frame of the National Centre for Competence in Research PlanetS supported by the Swiss National Science Foundation (SNSF). MRM, HMS, and SD are pleased to acknowledge this financial support of the SNSF. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research made use of Astropy9, a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018), Numpy (Harris et al. 2020), Matplotlib (Hunter 2007), Scipy (Virtanen et al. 2020), and Numba (Lam et al. 2015).
Appendix A Alternative data reduction
The top and bottom rows of Figure A.1 respectively show the reduction of the science data cube using the GreeDS and MAYONNAISE algorithms. The interested reader is referred to the original papers describing the pipelines, Pairet et al. (2018) and Pairet et al. (2021). The main parameters for the different reductions are reported in the individual images of Figure A.1 and are the rank number for GreeDS and the disk regularization for MAYONNAISE (using a rank of six for the GreeDS preliminary step). The other parameters were set to the default values: a central mask of eight pixels, 10,000 iterations, and a tolerance threshold of 10−4 for the convergence of the algorithm. The images do not recover the flux of the disk along the minor axis nor the DI-sNMF reduction (Fig. 1), but the arc-like structure close to the major axis of the disk was recovered.
 |
Fig. A.1 Data processing using the GreeDS and MAYONNAISE algorithms (top and bottom, respectively). The main parameters for the reduction (rank and regularization parameters) are reported in each image. The scaling is linear up to the 99.9 percentile and was reevaluated for each panel. |
Appendix B Additional images
FigureB.1 shows simulated images in total intensity and polarimetry using an HG-phase function with ɡ = 0.5 (similar to the results from Matthews et al. 2017). It shows that the arc survives a change in the asymmetry parameter.
Figure B.2 shows images in polarized intensity integrated over the size distribution when taking into account the variation of Qsca with the grain size and the waviness of the size distribution. It should be noted that the simulated images that include both the effects of Qsca and the wavy size distribution look more similar to the polarimetric observations than the images in the middle and top panels of the figure.
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Aumann, H. H., Beichman, C. A., Gillett, F. C., et al. 1984, ApJ, 278, L23 [CrossRef] [Google Scholar]
- Ballering, N. P., Rieke, G. H., Su, K. Y. L., & Montiel, E. 2013, ApJ, 775, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonnefoy, M., Milli, J., Ménard, F., et al. 2017, A&A, 597, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]
- Chen, C. H., Mamajek, E. E., Bitner, M. A., et al. 2011, ApJ, 738, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Mittal, T., Kuchner, M., et al. 2014, ApJS, 211, 25 [Google Scholar]
- Chen, C., Mazoyer, J., Poteet, C. A., et al. 2020, ApJ, 898, 55 [CrossRef] [Google Scholar]
- de Boer, J., Langlois, M., van Holstein, R. G., et al. 2020, A&A, 633, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [Google Scholar]
- Dohlen, K., Saisse, M., Origne, A., et al. 2008, SPIE Conf. Ser., 7018, 701859 [NASA ADS] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [Google Scholar]
- Dominik, C., Min, M., & Tazaki, R. 2021, Astrophysics Source Code Library [record ascl:2104.010] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [Google Scholar]
- Feldt, M., Olofsson, J., Boccaletti, A., et al. 2017, A&A, 601, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flasseur, O., Thé, S., Denis, L., Thiébaut, É., & Langlois, M. 2021, A&A, 651, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jang-Condell, H., Chen, C. H., Mittal, T., et al. 2015, ApJ, 808, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Jovanovic, N., Martinache, F., Guyon, O., et al. 2015, PASP, 127, 890 [NASA ADS] [CrossRef] [Google Scholar]
- Juillard, S., Christiaens, V., & Absil, O. 2022, A&A, 668, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kral, Q., Matrà, L., Kennedy, G. M., Marino, S., & Wyatt, M. C. 2020, MNRAS, 497, 2811 [NASA ADS] [CrossRef] [Google Scholar]
- Lam, S. K., Pitrou, A., & Seibert, S. 2015, in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, LLVM ‘15 (New York, NY, USA: Association for Computing Machinery) [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, PNAS, 111, 12661 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, S. 2022, ArXiv e-prints [arXiv:2202.03053] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Matthews, E., Hinkley, S., Vigan, A., et al. 2017, ApJ, 843, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Mazoyer, J., Arriaga, P., Hom, J., et al. 2020, SPIE Conf. Ser., 11447, 1144759 [NASA ADS] [Google Scholar]
- Milli, J., Mouillet, D., Lagrange, A.-M., et al. 2012, A&A, 545, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milli, J., Vigan, A., Mouillet, D., et al. 2017, A&A, 599, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Hovenier, J. W., & de Koter, A. 2005, A&A, 432, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Min, M., Dominik, C., Debes, J. H., & Schneider, G. 2013, A&A, 549, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newville, M., Otten, R., Nelson, A., et al. 2021, https://doi.org/10.5281/zenodo.4516651 [Google Scholar]
- Olofsson, J., Samland, M., Avenhaus, H., et al. 2016, A&A, 591, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, J., van Holstein, R. G., Boccaletti, A., et al. 2018, A&A, 617, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, J., Milli, J., Bayo, A., Henning, T., & Engler, N. 2020, A&A, 640, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, J., Thébault, P., Kennedy, G. M., & Bayo, A. 2022a, A&A, 664, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, J., Thébault, P., Kral, Q., et al. 2022b, MNRAS, 513, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Pairet, B., Cantalloube, F., & Jacques, L. 2018, arXiv e-prints, [arXiv:1812.01333] [Google Scholar]
- Pairet, B., Cantalloube, F., & Jacques, L. 2021, MNRAS, 503, 3724 [Google Scholar]
- Ren, B., Pueyo, L., Zhu, G. B., Debes, J., & Duchêne, G. 2018, ApJ, 852, 104 [Google Scholar]
- Ren, B., Pueyo, L., Chen, C., et al. 2020, ApJ, 892, 74 [Google Scholar]
- Ren, B., Choquet, É., Perrin, M. D., et al. 2021, ApJ, 914, 95 [CrossRef] [Google Scholar]
- Schneider, G., Grady, C. A., Hines, D. C., et al. 2014, AJ, 148, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Debes, J. H., Grady, C. A., et al. 2018, AJ, 155, 77 [Google Scholar]
- Strubbe, L. E., & Chiang, E. I. 2006, ApJ, 648, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., & Augereau, J.-C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [Google Scholar]
- van Holstein, R. G., Snik, F., Girard, J. H., et al. 2017, in Techniques and Instrumentation for Detection of Exoplanets VIII, ed. S. Shaklan, 10400, International Society for Optics and Photonics (SPIE), 1040015 [NASA ADS] [Google Scholar]
- van Holstein, R. G., Girard, J. H., de Boer, J., et al. 2020, A&A, 633, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wahhaj, Z., Milli, J., Romero, C., et al. 2021, A&A, 648, A26 [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A&A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [Google Scholar]
Available at https://irdap.readthedocs.io/en/latest/
Available at https://github.com/seawander/nmf_imaging
The PCA was performed on the science cube itself, not making use of the calibrator cube. In Fig. 1, we used two components.
Available at https://github.com/joolof/betadisk
Available at https://github.com/cdominik/optool
See the discussion in Olofsson et al. (2020) on the impact of the vertical height on the phase function. In the case of HD 129590, Kral et al. (2020) reported the presence of gas, and Olofsson et al. (2022a) showed that gas-bearing disks are most likely vertically thin at near-IR wavelengths, justifying the assumption of a thin disk.
As discussed in Mulders et al. (2013), this should also impact the Qsca values, but for the sake of simplicity, we opted not to include this effect in our calculations.
All Figures
 |
Fig. 1 SPHERE-IRDIS observations of the disk around HD 129590. Left panel: DI-sNMF total intensity reduction. The detection of the birth ring and the presence of a faint arc are highlighted by two arrows in the left panel. The inset in the left panel also shows the DI-sNMF reduction with the birth ring (best-fit from Olofsson et al. 2022b) and the arc highlighted. Top-right panel: PCA total intensity reduction. Bottom-right panel: Qϕ polarized intensity reduction. The location of the birth ring is shown in the Qϕ image as a solid black line. For each image, the central mask has a radius of 0.125′′, and the color scale is linear. North is up, east is left, and the pixel scale is of 12.26 mas. |
| In the text | |
 |
Fig. 2 Simulated disk images for total intensity (top panels) and polarized intensity (bottom panels) for different narrow intervals of β, and the average value of β is reported in each panel. The value of the asymmetry parameter ɡ is set to 0.7 for all images. The scaling is linear and adjusted to the 99.9 percent for all frames. The images are convolved with a 2D Gaussian with a standard deviation of two pixels. |
| In the text | |
 |
Fig. 3 Total intensity and polarimetry images integrated over the full size distribution between βmin and βmax with a square root scaling. |
| In the text | |
 |
Fig. 4 Ratio of β and Qsca scattering efficiencies (different y axis) as a function of the grain size. The vertical line denotes the blow-out size for which β = 0.5 (horizontal line). |
| In the text | |
 |
Fig. 5 Total intensity images integrated over the full size distribution between βmin and βmax The different panels show the differences when accounting for the wavy size distribution or the variation of Qsca as a function of s. The images are shown with a square root scaling to better highlight the regions outside the birth ring. |
| In the text | |
 |
Fig. 6 Surface brightness as a function of the scattering angle extracted in concentric annulii, accounting for the inclination and position angle of the disk, with increasing deprojected stellocentric distances r (in arc-sec). For clarity, the profiles have been offset and the horizontal lines show the zero point in the top panel, while no offset has been included for the bottom panel to best compare the different profiles. The fainter lines in the top panel show the best-fit with an HG-phase function (the ɡ values are reported in the legend). The gray-shaded areas show the scattering angles that are not accessible to us for an inclination of 82°. |
| In the text | |
 |
Fig. A.1 Data processing using the GreeDS and MAYONNAISE algorithms (top and bottom, respectively). The main parameters for the reduction (rank and regularization parameters) are reported in each image. The scaling is linear up to the 99.9 percentile and was reevaluated for each panel. |
| In the text | |
 |
Fig. B.1 Same as Figure 2 but for ɡ = 0.5 instead of 0.7. |
| In the text | |
 |
Fig. B.2 Same as Figure 5 but in polarized intensity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.