EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 666 (October 2022) A&A, 666 (2022) A171 Full HTML
Open Access
Issue
A&A
Volume 666, October 2022
Article Number A171
Number of page(s) 24
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202243900
Published online 25 October 2022

© L. Doorenbos et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1 Introduction

In the last 20 yr, numerous digital surveys such as the Sloan Digital Sky Survey (SDSS, York et al. 2000), the Kilo Degree Square Survey (KiDS, de Jong et al. 2015), the Panoramic Survey Telescope and Rapid Response System (Pan-STARRS, Magnier et al. 2020), the Dark Energy Survey (DES, Dark Energy Survey Collaboration 2016), and the Hyper Suprime-Cam Subaru Strategic Program (HSC SSP, Aihara et al. 2019) have greatly improved our knowledge of the Universe by exploring deep and wide areas of the sky through multi-wavelength imaging campaigns. In the coming years, new multi-band wide-field survey projects, such as the Vera C. Rubin Observatory Legacy Survey of Space and Time (Rubin-LSST, Ivezic et al. 2019), Euclid (Scaramella et al. 2022), the Nancy Roman Telescope (formerly the Wide-Field Infrared Survey Telescope or WFIRST, Green et al. 2012), and the James Webb Space Telescope (JWST, Álvarez-Márquez et al. 2019), will further increase the amount of observational data by orders of magnitudes. Most of these future surveys will produce photometric data for several million sources each night. However, as spectroscopic follow ups for even a small fraction of the observed sources will be unfeasible, there is the need for algorithms capable of exploiting photometric information to classify, or at least identify, interesting candidates to be further investigated. It comes as no surprise that, in recent years, much work has been devoted to implementing and fine tuning fast and self-adaptive learning methods for prediction, classification, and visualization (in other words, for understanding data), inducing the exploitation of astroinformatics solutions, for instance the paradigms of machine and deep learning (Baron 2019; Longo et al. 2019; Fluke & Jacobs 2020; Lecun et al. 1998; D’Isanto & Polsterer 2018; Schaefer et al. 2018), replacing more classical methods considered inefficient in the big data regime.

We can roughly subdivide the machine learning (ML) algorithms into two broad classes. The first, which is probably the most used, is called supervised. Such methods rely on the availability of a set of data for which we believe to possess some ground truth (labels) that is used to train the algorithm. The other possibility is to have an unsupervised model, working on the data without any or almost any a priori knowledge. In this case, the labels (if any) are used only a posteriori to analyze and understand the results. It goes without saying that, with a supervised approach, the interpretation of the results is by far easier and that such methods can be more easily tailored to solving a specific problem. This explains why, so far, the number of works dealing with supervised methods is much larger (see a few examples: Weir et al. 1995; Kim et al. 2011; Brescia et al. 2013; D’Isanto et al. 2018; Delli Veneri et al. 2019; Schmidt et al. 2020; Kinson et al. 2021; Wenzl et al. 2021) than those using unsupervised approaches. Nonetheless, there are several successful examples of unsupervised approaches being used to solve astrophysical problems (e.g., Masters et al. 2015; Baron & Poznanski 2017; Frontera-Pons et al. 2017; Mislis et al. 2018; Castro-Ginard et al. 2018; Razim et al. 2021; Ofman et al. 2022).

Supervised ML methods imply the necessity of a training set derived from real data or simulations. However, in the case of real data, multi-band photometric observations cannot provide a full understanding of the physical processes at work and even spectroscopic observations are seldom fully representative of the complexity of the parameter space describing our Universe. Masters et al. (2015), for instance, showed that there are always portions of the parameter space left under-sampled (if not unexplored) and this is even more true when dealing with rare objects for which there are very few labels (if compared with more common objects).

The vast majority of unsupervised solutions can be regarded as clustering or pre-clustering methods, such as those devoted to the reduction of dimensionality (Bishop 2006). Under-sampled or rare objects are usually penalized in these kinds of representations, because they seldom succeed in creating a cluster on their own.

At the boundary between the two approaches lies the field of one-shot learning, where only a single labeled sample is available per class of interest (Wang et al. 2020). We apply this paradigm here as it has the potential to combine the best of both worlds: it removes the need for the expensive and often unfeasible process of collecting a large labeled dataset inherent to supervised methods, while at the same time removing the problem encountered with unsupervised methods that have trouble with rare and under-sampled objects.

In this work, we present ulisse (automatic Lightweight Intelligent System for Sky Exploration), a one-shot method capable of retrieving objects closely related to a given input, and apply it directly to multi-band images1. The idea behind our method is relatively intuitive: we transform the image of a given source (referred to as a prototype hereafter) into a set of representative features, after which we use this information to look for other objects similar to the prototype in the feature space, which should translate to similarity in the astronomical sense. The power of this method comes from the fact that even if we take a rare object as a prototype, the method allows us to search for similar objects in the dataset, thus bypassing the need for a large and well-sampled training set, and to provide a reliable list of candidates for follow-up observations, thus opening the way to the construction of a reliable training sample for supervised methods.

In order to test the method, we apply it here to the detection of active galactic nuclei (AGN).

The identification of AGN in the optical band is not trivial because of the strong contamination from the host galaxy and obscuration by the circumnuclear or galactic dust. This imposes a whole set of problems, which can be resolved with the use of multi-wavelength observations (from radio to X-ray) and the combination of different selection techniques. A proper AGN selection plays a crucial role in the study of the formation and evolution of supermassive black holes (SMBHs; Brandt & Hasinger 2005; Merloni 2016; Hickox & Alexander 2018) and their feedback on the host galaxies (Fabian 2012; Kormendy & Ho 2013; Heckman & Best 2014; Thacker et al. 2014). The identification of AGNs will be an important task for all future surveys such as the Rubin-LSST, because the new data will allow for the study of the formation and co-evolution of SMBHs, their host galaxies, and their dark matter halos. Furthermore, the classification of AGNs is also important for other science cases, because they need to be handled in an independent way with respect to standard galaxies when deriving, for example, photometric redshifts (Brescia et al. 2019; Euclid Collaboration 2020).

The search for candidate AGNs in surveys has been performed in the past with ML models applied to photometric tabular data (Cavuoti et al. 2013; Fotopoulou & Paltani 2018; Chang et al. 2021; Falocco et al. 2022) or to their variability (Palaversa et al. 2013; D’Isanto et al. 2016; Sánchez-Sáez et al. 2019; Faisst et al. 2019; De Cicco et al. 2021). More recently, there was also an attempt to use deep neural networks for the same task (Chen 2021).

A concurrent work by Stein et al. (2022) presents a similar approach to ours for the detection of astronomical objects, where the authors perform similarity searches on images and apply this method to the detection of strong gravitational lenses. Contrary to our approach, rather than pre-trained features, these authors make use of self-supervised pre-training.

The present paper is structured as follows: in Sect. 2, we present our method, while in Sect. 3 we describe our data sample and present the studied prototypes. Section 4 is devoted to the presentation of the experiments and their results. Section 5 contains a discussion of the results together with an analysis of the limitations of the method and some possible improvements. Finally, in Sect. 6 we present brief conclusions.

2 Method

For ulisse, we make use of the features extracted from a convolutional neural network (CNN) that has been pretrained on a general large-scale dataset and then finds relevant objects through a nearest neighbor search. We describe each of the architecture components in the following paragraphs.

2.1 Convolutional neural networks

In the context of classification, convolutional neural networks usually consist of two parts (Schmidhuber 2015): the first transforms the input image into a feature vector through a series of convolutional layers, pooling layers and activation functions (described below) and, in practice, operates as a feature extractor. The second part takes these features and uses them to perform the actual classification task. Usually this second part consists of a multi-layer perceptron (MLP, McCulloch & Pitts 1943; Rosenblatt 1958) neural network.

The convolutional layers shift a number of small windows (kernels) over the input, computing a weighted average of the local surroundings, obtaining the so-called feature maps as the output, which indicate how strongly a given location correlates with the window. The weights of these windows are learned by the model itself.

Pooling layers decrease the size of these feature maps by replacing each location in the input with an aggregate statistic derived from its rectangular neighborhood. The size of this neighborhood is set by the user. Commonly used examples are average pooling, which outputs the average value within the window, and max pooling, which reduces a region to its maximum value.

The activation functions are applied, with the goal being to introduce nonlinearity in the feature representation. A common example is the ReLU (Rectified Linear Unit) activation function, which sets the negative part of its input to zero, f(x) = max(0, x).

The feature-extractor part of the algorithm is followed by an MLP, consisting of one or more fully connected layers, which performs the actual classification of the input based on the features obtained in the previous part. In an MLP, a fully connected layer connects every input neuron to every output neuron. The final layer outputs a vector with as many elements as the number of classes and the neuron with the highest value identifies the final decision. The model is optimized with respect to a loss function end-to-end by forward propagation and error back-propagation (Bishop 2006; Goodfellow et al. 2016).

thumbnail Fig. 1

Three objects in our sample which most strongly activate features 11, 41, 541, 835, and 1073 (arbitrarily chosen for visualization), together with their feature maps. We provide these for all 1280 features at http://dame.na.astro.it/ulisse.

2.1.1 Pretraining

Training a CNN on a large and varied dataset allows it to learn a diverse and general set of features, which should be useful beyond the original task. These features are often used as the starting point for complex tasks in another domain (the target domain), with the aim being to avoid labeling the large amounts of data often needed to train a model from scratch (Pan & Yang 2009). This concept is known as transfer learning and has proven very successful in many domains (e.g., astronomy, Awang Iskandar et al. 2020; Martinazzo et al. 2021; malware classification, Prima & Bouhorma 2020; earth science, Zou & Zhong 2018; and medicine, Ding et al. 2019; Esteva et al. 2017; Kim et al. 2021; Menegola et al. 2017).

The typical large-scale dataset of choice used for training is ImageNet (Deng et al. 2009) which contains around 1.3 million images, where the original task was to classify each image into one of 1000 classes. In practice, when moving to the target domain, the second part of the architecture described above, namely the fully connected layers of the pre-trained network (the classifier), are discarded, as the new domain does not contain the same classes. The feature-extracting part of the network is then used to tackle the target task. As an additional benefit of this approach, no fine-tuning of the target domain is needed, thus reducing the training time to almost zero and making it directly applicable to any new dataset.

2.1.2 Feature extraction

In order to obtain our features, we first extract the feature maps (7 × 7 pixels each) from the final convolutional layer of the pre-trained neural network. In order to reduce their dimensionality, we then average over the spatial dimensions. As a result, the features represent image-level properties.

In deep learning, it is a common understanding that the deeper the layers in the network, the higher the level of abstraction of the extracted features (Goodfellow et al. 2016). Our approach is therefore based on the assumption that objects whose images share many deep features with the prototype (i.e., that are close together in this feature space) have also the same morphological properties. As further discussed in the coming sections, we wish to emphasize that because we are working with multi-band images, in this context, morphology must be intended in a broader sense, because we also take variations in the color distribution into account implicitly.

Throughout this work, we use an EfficientNet-b0 as the CNN from which we obtain the features; this is a specific type of CNN architecture (Tan & Le 2019) that was trained for classification on ImageNet. Its penultimate layer consists of 1280 channels, leading to a 1280-dimensional feature descriptor for each image.

We note that the features are extracted from the model, and were derived from natural images (i.e., heterogeneous images of everyday objects or scenes such as cats, cars, rivers, and so on), rather than astronomical ones. For this reason, they are not directly interpretable. Nonetheless, we can get an idea of the patterns that individual features are looking for by looking at the images in our dataset that most strongly activate them. We show this for the five cases in Fig. 1, where it becomes clear that different features are focusing on different aspects of the image. We provide these visualizations for each of the 1280 features at http://dame.na.astro.it/ulisse. With reference to Fig. 1, we need to stress that even though the similarity of the objects is defined through a complex combination of features, in some cases it is possible to recognize specific patterns that are associated to a given feature. For instance, feature 41 seems to be activated by extended objects with a bright nucleus, while feature 541 responds most strongly to narrow objects with some sort of bulge.

2.2 ulisse

These pretrained features are used by ulisse to identify objects with similar properties. This is done by performing a similarity search in the feature space. Given a prototype object, the closest objects in this feature space provide a list of candidate lookalikes for the prototype of interest. A schematic of the proposed method is shown in Fig. 2.

Formally, given a prototype image xq, we wish to retrieve its nearest neighbors from a dataset 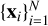{ xi }i=1N$\left\{ {{{\bf{x}}_i}} \right\}_{i = 1}^N$. For an image xi, we denote its pretrained feature representation as f(xi) ≡ fi We find the nearest neighbors by their Euclidean distance in this pretrained feature space (Hastie et al. 2009). Hence, we find those objects xi that minimize d(xq, xi) = ||fq − fi||2. With the use of acceleration structures such as k–d trees, which allow for the efficient computation of nearest neighbor searches, these lookalikes can be found extremely quickly after their initial construction.

If no validation data are available, ulisse can be applied by simply returning the n closest objects in the dataset as a list of candidates (measured in feature space, not in terms of astronomical distance), where n is set by the user. However, if we do have access to a validation set (even if it is limited), we can use this to measure our desired performance metric as a function of the distance of the lookalike from the prototype. We can then use this information determine a threshold on the distance for use on new data. For instance, if our aim is to retrieve AGN, we can determine until which distance from our prototype the fraction of AGN among the retrieved objects from the validation set remains high, and select all objects that fall within this distance from our target dataset.

More specifically, one can choose the furthest object xf at which point the selected sample still gives a good performance, with distance t = ||fq − ff||2. Then, on the target dataset, all objects from 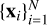{ xi }i=1N$\left\{ {{{\bf{x}}_i}} \right\}_{i = 1}^N$ satisfying d(xq, xi) ≤ t are selected.

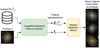thumbnail Fig. 2

Overview of ulisse.

3 Dataset

In order to assess the result of this method, we need a sample with well-known object classification. For this purpose, we choose to retrieve thumbnails for the sample used in Torbaniuk et al. (2021).

3.1 Dataset details

The sample of Torbaniuk et al. (2021) is based on the galSpec catalog of galaxy properties2 produced by the MPA-JHU group as a subsample from the main galaxy catalog of the eighth data release of the Sloan Digital Sky Survey (SDSS DR8, Brinchmann et al. 2004). This sample has been cleaned by removing duplicates and objects with low-quality photometry using the basic photometry processing flags recommended by SDSS3. The objects were classified using the so-called BPT-diagrams (from the names of the proposers: Baldwin, Phillips & Terlevich, Baldwin et al. 1981) as: star-forming galaxies “SFG”, “AGN”, and “Composite” according to the ratios of four specific emission lines in their optical spectra (Kauffmann et al. 2003; Kewley et al. 2006). Brinchmann et al. (2004) expanded these selection criteria and added two additional classes of objects with low signal-to-noise lines (low-S/N SFG and AGN). In our work, we used the naming “SFG” for both low-S/N SFG and SFG, and “AGN” for both AGN and low-S/N AGN. At the same time, our sample also contains a significant fraction of objects with weak or no emission lines, which remain unclassified due to limitations of the BPT-diagram (see Table 1). Moreover, some SFGs may contain a low-luminosity AGN, which may not be classified by the BPT-diagram because the emission of the star-forming processes in the host galaxy will dominate the optical spectrum. To address these problems and improve the selection, we added X-ray detections from the XMM-Newton Serendipitous Source Catalog (3XMM-DR8, Rosen et al. 2016). The total number of objects in our optical sample observed by XMM-Newton and their fraction in each class are presented in Table 1 (X-ray MOC subsample). X-ray AGN were classified according to the X-ray selection criteria described in detail in Torbaniuk et al. (2021), that is, large X-ray luminosity or X-ray/optical ratio.

For each object in our sample, we extracted thumbnails from the Sloan Digital Sky Survey Data Release 16 (SDSS DR16, Eisenstein et al. 2011; Blanton et al. 2017; Ahumada et al. 2020; York et al. 2000) using the Image Cutout service4. This service allows the retrieval of JPEG images composed of the three inner SDSS bands (g, r and i) for any portion of the sky observed by SDSS just based on its coordinates. In this work, we decided to retrieve 64 × 64 pixel thumbnails. This is based on initial experiments with 48 × 48, 55 × 55, 64 × 64, and 73 × 73 pixel thumbnails, where we found that 64 × 64 gave the best results. As the images are reduced to 56 × 56 pixels after center cropping, they correspond to a size of ~22.2 × 22.2 arcsec (the SDSS pixel scale is 0.396 arcsec per pixel). The choice of the thumbnail size is important because a small size may lead to cutting the edges of an extended object, while a uselessly large thumbnail could contain more than one object, thus affecting the characteristic extracted by our method. Recall that as we average our features over the spatial dimensions, they describe image-wide properties.

There is no proper way to completely eliminate both effects, but considering our preliminary experiments and the reference objects themselves (see Sect. 3.2), we decided on 22.2 × 22.2 arcsec as a good compromise. Although the spectroscopic information comes from an earlier data release (DR8), we decided to retrieve the images from the latest version of SDSS in order to benefit from any possible improvements or bug removals of the pipeline. Considering the redshift range covered by our sample, these thumbnails correspond to physical sizes ranging from ~50 pc up to ~ 110 kpc on a side.

As our goal is to show the validity of our method, rather than to obtain results for the whole sample, we create a smaller subset of the data for efficient computation. To this end, we randomly shuffle the coordinates, and take the first 100 000 objects. In some cases, the Image Cutout service fails to retrieve a thumbnail, and therefore we are left with 99 991 images as our dataset. This is denoted with Random in Table 1, where we see that its proportions are almost equal to that of the whole sample. The percentage of sources classified as AGN according to the BPT selection in the Random sample is 12% (see Table 1) and is used as the random guess baseline to test our method.

Table 1

Summary of the different datasets studied in this work.

Table 2

Summary of the thumbnails used as AGN prototypes in our work.

3.2 Prototypes

In order to detect candidate AGN, we need to select a set of prototypes that contains “true” AGN and nonAGN confirmed by some reliable criteria. As X-ray emission is a good (and least contaminated) tracer of accretion processes, we selected the two groups of prototypes (AGN and nonAGN) within the X-ray MOC subsample in Table 1 based on X-ray criteria. Furthermore, numerous studies show that AGN may be detected in galaxies of different morphological types, however they show some preference for star-forming galaxies (probably due to there being a larger reservoir of cold gas available for SMBH accretion in star-forming galaxies compared to quiescent ones; see Lutz et al. 2010; Mendez et al. 2013; Rosario et al. 2013; Stemo et al. 2020). We therefore selected prototypes that represent a variety of morphological types. The list of eight AGN prototypes according to the X-ray criteria is presented in Table 2, while five nonAGN prototypes are presented in Table 3. For the AGN prototypes, we selected a couple of blue spiral galaxies (i.e., with younger stellar population and ongoing star-formation processes, #2,8), elliptical galaxies with red color (i.e., older stellar population and quenched star-formation, #3,5), a transition galaxy (#4) with red color and spiral structures, a peculiar galaxy with possible arms or shell-like features which may be caused by past galaxy interactions (#1), and ring (#7) and bar (#6) galaxies. In addition to X-ray AGN identification, these prototypes have also been classified using the BPT-diagram. Prototypes #1, 3, 5, and 7 are identified as AGN (i.e., the AGN signatures dominate the optical spectrum, and #2, 4, and 6 are SFGs according to the BPT-diagram (i.e., the star-forming signatures dominate the optical spectrum). At the same time, the prototype#8 is marked as a “Composite” displaying the contribution from both an AGN and star-forming processes. As the ulisse performance may depend on the morphology of the host galaxy rather than the presence of an AGN, we also added nonAGN prototypes to our study. The selection of nonAGN prototypes was performed by a similar approach applied to AGN-prototypes selection: we chose elliptical (#9, 10) and spiral galaxies with blue (#11, 13) and red color (#12). In this case, three spiral galaxies are classified as SFG according to the BPT-diagram, while the ellipticals remain unclassified due to the absence or weakness of emission lines in their optical spectra.

It should be noted that in Tables 2 and 3 we used the 100 × 100 explorer images, while our experiments were performed based on 64 × 64 thumbnails.

Table 3

Overview of the thumbnails used as nonAGN prototypes in our work.

4 Experiments and results

In this section, we present our results for the one-shot AGN detection, along with an analysis of the morphology and color of each prototype object and their contribution to the overall AGN fraction (Sect. 4.2). In addition, in Sect. 4.3 we introduce a recursive application of our method as a promising technique to retrieve a purer sample with a larger number of candidates.

4.1 AGN detection results

As mentioned in the previous section, for each object in our sample we have labels according to the BPT diagram (see Table 1), while the labels from the X-ray classification are available only for the X-ray MOC subsample. To begin our experiment, we used the g, r, i color-composite thumbnails. The results corresponding to each prototype are visualized as the number of objects of different classes (AGN, SFG etc.) selected by our method versus the distance from our prototype (see Tables A.1, A.2 for AGN prototypes and Table A.3 for non-AGN prototypes). As no validation set is available, we set the number of objects n retrieved by ulisse to 300 nearest neighbors. We chose this number in order to study the variation of AGN fraction with distance. However, in practice, the choice of n depends on the purpose of the user and goals of the study.

The experiments for the 8 “AGN” prototypes retrieve on average 34.0% objects also labeled as AGN over all 300 nearest neighbors. However, this fraction varies from object to object. For instance, for prototypes #1,3, and 5, our method retrieved ~40% of AGN (on average) within the 300 nearest neighbors. Taking into account also composite objects (i.e., with spectral signatures both from the AGN and star formation), the resulting fraction of AGN + composite reaches ~55%. The rest of the sources belong to the SFG and Unclassified classes (see details in Table 4). In the case of prototype #4, the fraction of AGN reached 53% (up to 65% for AGN + composite). On the other hand, ulisse retrieved a relatively low fraction of AGN (21–28%) for prototypes #2,6, and 8 (close to 40% for AGN + composite, see Table 4). However, in general, the retrieved AGN fraction for all AGN prototypes significantly exceeded the value expected by the random guess baseline, which is 12% according to the BPT selection presented in Table 1.

In the case of nonAGN prototypes (objects #9–13 in Table 3), we expect a smaller number of AGN to be retrieved. For instance, for prototypes #9 and 10 labeled as “Unclassified” according to the BPT-diagram, ulisse found only 21% of AGN, while the rest of the resulting objects are labeled as “Unclassified”. Similar results were obtained for prototypes #11 and 13 labeled as “SFG”, where ulisse retrieved only 14.3% and 1.7% AGN. In the case of prototype#12 (SFGs according to BPT-diagram), the method retrieved a relatively large fraction of AGN compared to other nonAGN prototypes mentioned above, which is also comparable to the resulting percentage of SFGs.

The BPT classification is not always able to detect the presence of an AGN and disentangle nuclear from star-formation activity, especially for low-S/N spectra. For this reason, we decided to repeat our experiments using the X-ray MOC subsample of sources observed by XMM-Newton (Table 1) and the X-ray classification criteria. The resulting AGN/nonAGN fraction as a function of distance is presented in Tables A.1, A.2 (for AGN prototypes #1-8), and A.3 (nonAGN prototypes #9-13). The percentage of AGN/nonAGN obtained by ulisse for all studied prototypes is presented in Table 4. The average retrieved AGN fraction ranges between 8% and 12%, which again exceeds the percentage of AGN expected by the random guess baseline for X-ray MOC sample (4%; see Table 1). The same test with the X-ray MOC sample again yields lower AGN fractions for nonAGN prototypes (see Table4). Appendix B presents the closest 25 neighbors returned by ulisse for each AGN/nonAGN prototype (see Figs. B.1–B.12).

Table 4

Fractions of SFG, Composite, AGN, and Unclassified objects for each of the 13 prototypes over their 300 nearest neighbors.

4.2 Disentangling morphology and color

Traditionally, AGN identification relies on different selection criteria based on their photometric and spectroscopic information (such as color-color diagrams (Richards et al. 2002, 2005; Schneider et al. 2007, 2010; Chung et al. 2014) and spectral lines ratios, (Heckman 1980; Kauffmann et al. 2003; Kewley et al. 2006)). As explained above, our experiments used color-composite g, r, i thumbnails to recognize the different classes of sources. To assess whether ulisse results are mainly based on the morphological features of the prototypes or on their colors, we performed an additional set of tests using only single optical bands.

In Table 5, we present the fractions of AGN, SFG, Composite, and Unclassified objects based on single (g, r or i-band) band. Considering the fraction averaged over the eight AGN-prototypes, we found that ulisse returned a smaller fraction of AGN and Composite using only single-band images. Obviously, the lower efficiency implies an average increase in the fraction of SFG and Unclassified classes among the sources retrieved with the use of a single band. In particular, the g-band showed the lowest AGN retrieval efficiency (23.9%) among the three bands (30.3% and 29.4% for r and i bands, respectively). For nonAGN prototypes, we observed similar trends (see Table 5). Table A.4 presents the fractions of AGN, SFG, Composite, and Unclassified objects as a function of distance for prototypes #2,3, and 6 obtained based on a single band or on their combination.

4.3 Recursive application

While ulisse can return hundreds of candidates for a single prototype, the success rate typically drops with the number of returned objects, that is with the distance from the prototype in the feature space. Due to this effect, in Sect. 4.1, we find that retrieval of AGN is most effective using the closest neighbors, typically the nearest 20-30 objects returned by our method. One possible way to keep the purity high while increasing the number of sources is to apply ulisse in a recursive way. We do this by using one of the resulting candidates as a prototype for the next step of the selection, and in this section verify if this recursive technique returns a sample with equal or higher success rate compared to our initial approach described in Sect. 4.1.

Concretely, we select the closest object in feature space to our reference prototype and apply it as the prototype for the next step. As this closest object likely shares the most morphological and photometric properties with our reference prototype, it should also be the most likely to be an AGN. Then, at each next step we repeat the same procedure choosing the closest object to the reference object used in the previous step, but excluding objects considered in earlier steps. We set n = 25. Results can be found in Table 6, where we see that the recursive version has a slightly higher purity, and a lower standard deviation compared to the normal version, suggesting it might be more robust to the choice of prototype.

Using this setup, for the relatively unsuccessful prototype #2, we obtained a total of 89 objects excluding duplicates in five iterations, of which 38 are AGN (42.7%, see Table A.5). In contrast, the resulting AGN fraction setting n = 89 directly for prototype #2 would only result in 25.8% AGN.

We found this mostly beneficial when the chosen prototype did not score exceptionally well. For example, in the case of prototype #4, we obtain 87 objects of which 47.1% are AGN with five iterations of our recursive method, yet this is 63.2% if we simply set n = 87.

Table 5

Fractions of SFG, Composite, AGN, and Unclassified objects for each of the 13 prototypes over their 300 closest neighbors obtained based on a single band SDSS image (g, r or i band).

Table 6

Results obtained after five iterations of the recursive application of ulisse with n = 25.

5 Discussion

In Sect. 4, we present the AGN fraction retrieved by ulisse for AGN and nonAGN prototypes, and its correlation with the color and the morphological type of studied prototypes. Furthermore, we analyzed the possibility to improve our results with use of a recursive technique. In this section, we discuss and interpret our results, ulisse limitations, and possible future improvements.

5.1 Correlation between prototype properties and AGN fraction retrieved by ulisse

The traditional optical AGN-selection criteria are based on photometric and spectroscopic properties such as magnitudes, colors, the ratios of high- and low-excitation emission lines, and so on (Kauffmann et al. 2003; Hickox & Alexander 2018; Zhang & Hao 2018). However, AGN identification in the UV/optical band is nontrivial and faces several limitations. For instance, the so-called color-color diagrams can be used to distinguish distant bright quasars from stars in our Galaxy, because of the bluer color of quasars compared to stars (i.e., the peak of emission from an AGN accretion disk is located in the UV range; Shakura & Sunyaev 1973). At the same time, such color-color criteria do not work well for nearby, low-luminosity AGN, because the stellar emission of the host galaxy begins to dominate the AGN emission in the optical range. This issue may be partially resolved by a spectroscopic approach, for instance by the BPT-diagram, where the AGN identification relies on the ratios of emission lines in the optical spectrum (Kauffmann et al. 2003; Kewley et al. 2006), but even in this case we lose a large fraction of AGN due to the fact that the star-formation processes also contribute to the optical emission lines. In addition, all UV/optical selection criteria are inefficient to identify AGN obscured by circumnuclear and galactic dust (Hickox & Alexander 2018; Zhang & Hao 2018; Ji et al. 2022). Therefore, a more efficient AGN identification usually requires use of multi-wavelength observations including radio, IR, and X-ray bands (Mateos et al. 2012; Trump et al. 2013; Heinis et al. 2016; Agostino & Salim 2019).

In Sect. 4, we mentioned that the total fraction of AGNs in our sample according to the BPT diagram is only 12% (i.e., the random guess baseline of our method), while ulisse appears to be more effective than random selection in identifying AGN, yielding on average 34% of confirmed AGN for the eight prototypes studied here (see Table 4). At the same time, a detailed analysis of each separate prototype showed that this AGN fraction varies depending on the properties of the prototype: in general, the aGn selection efficiency for prototypes that visually belong to late-type galaxies (spiral morphology) is lower than for early-type galaxies (elliptical morphology).

For instance, for prototypes #2, 6, and 8, ulisse found on average only ~25% AGN (see Table 4). Such relatively low efficiency in selecting AGN can be due to several factors. Firstly, as we mentioned in Sect. 3, the BPT diagram separates AGN from star-forming galaxies based on the ratio of emission lines and therefore the source identification depends on the process that dominates the spectrum (AGN or star formation). The majority of spiral galaxies have strong ongoing star-formation whose emission can outshine less powerful AGN, which would then be classified as SFGs according to the BPT-diagram.

A low retrieval fraction is observed instead for #7 at small distances from the prototype; this could be due to the peculiar nature of this source both for its ring-like morphology and for the presence of a bright nearby star. However, overall the average efficiency settles on ~24%, not far from other late-type galaxies.

At the same time, our sample contains a sizeable fraction of so-called Composite objects, where AGN and star-forming emission contribute equally to the optical spectrum and cannot be easily separated (Kewley et al. 2006; Kauffmann et al. 2003). This fact allows us to combine the fraction of AGN and Composite objects obtained by ulisse, which gives us an average AGN content of ~42% for prototypes #2, 6, 7, and 8.

For prototypes #3 and 5, which have an early-type morphology, ulisse identified on average ~40% of the confirmed AGN (54% in the case of AGN + composite, see Table 4). The larger AGN retrieval efficiency obtained for prototypes with early-type morphology can be explained by the properties of passive galaxies, which typically have partially or completely quenched star-formation Thomas et al. (2002), Thom et al. (2012); this allows easier detection of the AGN emission with negligible contamination from the host galaxy.

The highest AGN fraction among the eight AGN prototypes was obtained by ulisse for prototype#4 (53.0%, and 65.4% of AGN + composite). This prototype shows the presence of a bright red nucleus, which means that ulisse tends to select sources with a high nuclear luminosity and possibly – due to the known correlation between bulge and BH mass – suggests a stronger AGN activity (Häring & Rix 2004; Kormendy & Ho 2013; McConnell & Ma 2013).

As mentioned above, an additional issue that may explain the differences in our AGN identification efficiency is the partial or complete obscuration of the nucleus in the optical band by circumnuclear and/or galactic dust. This effect is more significant for star-forming galaxies, because they usually show the presence of a strong dust component in the disk, which plays an important role in the star-forming processes, helping to cool the cold gas (Byrne et al. 2019; Lianou et al. 2019). However, AGN obscuration can also take place in some elliptical galaxies, which show peculiar morphology and unusual dust lanes (Goudfrooij 1995; Hirashita et al. 2015). In such cases, AGN detection is possible only at less affected wavelengths, such as IR or X-rays.

In discussing the results obtained for different prototypes, we may wonder whether the ulisse performance depends more on the morphology of the host galaxy than on the presence of an AGN. To understand if this is the case, we performed an additional test with nonAGN prototypes. As explained in Sect. 3.2, we chose several galaxies with different morphologies (prototypes #9-13 in Table 3). Table 4 shows that the resulting AGN fraction obtained by our method is smaller on average (19.2%) than that found for AGN-prototypes and there is a similar correlation with the properties of the host galaxy (see Table A.3). At the same time, ulisse was very effective in retrieving objects with a BPT class similar to the studied prototypes, specifically “Unclassified” and “SFG” for early-type and late-type systems, respectively.

Overall, the lower AGN fraction for nonAGN prototypes indicates that ulisse is able to not only retrieve galaxies with a similar morphology and color to the studied prototype, but also to detect AGN with some level of reliability. However, we should also mention that prototype #12 (see Table A.3) produced a relatively large AGN fraction (36.7%) compared to other nonAGN prototypes, and comparable to some of the AGN prototypes. In this case, the ulisse performance could be driven by the red color and bright central bulge of the spiral galaxy, similar to the AGN-prototype #4 (see Table A.2 and the discussion above).

Using the X-ray MOC sample (i.e., the sample of SDSS galaxies that fall within XMM-Newton footprint, see Torbaniuk et al. 2021), we performed several additional tests in order to avoid the limitations in the BPT classification method described above. Table 4 presents the AGN fraction obtained by ulisse based on the X-ray MOC sample. The average AGN fraction for AGN-prototypes#1–8 is ~12% while for nonAGN prototypes #9–13 this value is ~8%; on the other hand the random guess baseline is 4%.

For the individual prototypes, we observe similar trends to those seen for the BPT validation, that is prototypes with early-type morphology (#3, 5) produce in general higher AGN percentages (12%) compared to prototypes #2, 6–8 with spiral morphology (9.3%). While this result may seem to contradict recent studies that found that X-ray-selected AGN preferentially reside in gas-rich galaxies with active star formation (Lutz et al. 2010; Mullaney et al. 2012; Mendez et al. 2013; Rosario et al. 2013; Shimizu et al. 2015; Birchall et al. 2020; Stemo et al. 2020; Torbaniuk et al. 2021), in fact there is no disagreement here because we are selecting based on combined optical and X-ray data. The tests for nonAGN prototypes using the X-ray MOC sample show, again, an average lower percentage of retrieved AGN; specifically for prototypes #9 and 10, with elliptical morphology, we obtain ~7%–8%, while for prototypes #11–13 with spiral morphology this value varies from 2.7% to 11%.

In Sect. 3, we mention that ulisse uses SDSS images in three bands (g, r and i). To assess whether or not the color information actually improves the ulisse efficiency or the results are only driven by the source morphology, we performed a further set of tests based on single band images (see Sect. 4.2). Using single g, r, or i-band we found a decrease in the retrieved AGN and Composite fractions for almost all AGN prototypes compared to those obtained using the color information as well (the only exception is the peculiar ring-like galaxy; see Table 5).

Based on this set of experiments with single bands, we can say that despite the presence of peculiar cases, ulisse actually exploits the available information from the different bands to improve the efficiency in detecting objects with similar physical properties, although the morphology has a dominant role.

5.2 Possible ways to increase the AGN fraction

There are several possible ways to increase the fraction of AGN identified by ulisse. We mention above that the absolute number of sources n retrieved by ulisse depends on the goal of the study. In our work, we set n = 300 to explore the dependence of the AGN fraction on the “distance” from the template, but as we see in Sect. 4.1 the success rate is usually greater when using the closest neighbors (see Table A.1, A.2). In the case of prototypes #3 and 5, with elliptical morphology, the AGN fraction can reach 80% for the ten nearest objects (i.e., 8 of 10 objects retrieved by ulisse are AGN). At the same time, for prototype#4, ulisse was able to retrieve AGN with 100% efficiency for the ten nearest objects. A similar performance at low distances is also visible for prototypes #2, 6, and8 with spiral morphology; however, comparing to prototypes with elliptical morphology, we see a smaller efficiency (near 40-60% for the ten nearest objects). Furthermore, “spiral” prototypes seem to suggest a sharper decrease in the AGN fraction with increasing distance to the reference prototype than prototypes with elliptical morphology. A different result was obtained only for the peculiar ring-like prototype #7, which showed no AGN in the ten nearest objects (the number of AGN reached 20% only in the next 10-15 objects; see Table A.2). Therefore, on average, reducing the number of sources n would result in an increase in the AGN identification efficiency, but as a result we would obtain a smaller number of objects in the returned sample.

Moreover, the purity of the returned sample can be increased by applying our method in a recursive way. This makes use of the higher efficiency found among the closest neighbors, by iteratively choosing the next prototype as the closest new object instead of simply enlarging the number of returned objects using one reference prototype, therefore producing more robust results. In our work, we tested the application of this recursive technique (see details in Sect. 4.3), which resulted in a higher AGN fraction together with a lower variance compared to our general method. In this way, the application of a recursive technique may be the preferential path to explore ways to increase the total number of objects while preserving a high AGN retrieval efficiency.

On the other end, as we discuss in the previous section, our results are constrained by the use of optical images and optical BPT selection criteria. Thus, the resulting AGN fraction obtained by ulisse could be underestimated due, for example, to dust obscuration and/or contamination from star-forming processes in the host galaxy. To avoid or reduce this effect, we could try to extend our method using images at additional wavelengths such as IR or UV.

5.3 Computational time

Our method is based on two main steps. In the first step, all images are run through the pretrained neural network to extract the features. This step has to be done only once per dataset. The local run on a single NVIDIA GeForce™ RTX 20605 processes 100k images in 3–4 min. In the second step, we search for similarities to the chosen prototype within the entire dataset, comparing the features extracted in the previous stage. Using a k–d tree algorithm with k = 300, we can pre-compute a structure that significantly speeds up later searches. Building the tree takes around 25–30 s on the same machine; results for any given prototype are then retrieved within one second.

Hence, starting from scratch, the closest 300 objects to a given prototype are retrieved from a dataset of 100k images in approximately 5 min. Subsequently, the process speeds up significantly due to the availability of the features and k–d tree, and 300 objects for any subsequent prototype are returned within a matter of seconds.

In addition, we should mention that SDSS thumbnails used in this work are of 64 × 64 pixels in size, while our method had to rescale them to the size expected by the pretrained network (224 × 224 pixel). Therefore, using images with higher resolution can be a natural way to improve ulisse performance without loss of computational speed.

6 Conclusions

In this work, we present a new deep learning tool called ulisse (aUtomatic Lightweight Intelligent System for Sky Exploration) for the exploration of sky surveys. The core of our method is to extract a set of representative features for each object in the sample under investigation, thus creating a common “feature space” where we can search for objects with properties similar to a chosen prototype.

Our method relies on only a single image of the requested object prototype, making use of the first portion of a pretrained convolutional neural network, which transforms images into a set of representative features without requiring any specific astro-physical information. ulisse sorts all objects in the studied dataset according to the distance in this feature space (i.e., from the most similar to the least similar to the reference prototype). To verify the efficiency of ulisse, we applied it to an extremely challenging task: the selection of AGN candidates using SDSS images of the galSpec catalog. Based on the results obtained running ulisse on eight AGN and five nonAGN prototypes with different host galaxy morphologies and spectral properties, we arrived at the following conclusions:

  • Our method is effective in identifying AGN candidates, and is able to retrieve galaxy samples with an AGN content that varies from 21% to 53% for different prototypes, significantly larger than the average AGN content of 12% in our full sample (according to the BPT classification). When including “composite” sources (which also host an AGN by definition), the retrieved AGN fraction rises to 65%;

  • Our tests show that the ulisse performance is based on a combination of host galaxy morphology, color, and the presence of a central nuclear source. In fact, the retrieved AGN fraction for AGN prototypes is significantly higher on average than for nonAGN prototypes;

  • Despite being capable of obtaining reliable results even using one single band, ulisse is capable of combining the information coming from different bands, thereby increasing its efficiency in identifying objects sharing similar physical properties;

  • We find ulisse is more effective in retrieving AGN in early-type host galaxies compared to prototypes with spiral/late-type properties;

  • The AGN retrieval efficiency is generally greater for neighbors that are closer to the prototype (i.e., the first 20–30). Thus, depending on the purpose of the study, ulisse can be used to retrieve either a higher percentage of AGN in a smaller sample, or a larger sample with lower AGN content. This dichotomy can be reduced using the recursive approach.

In light of the results described in this work and the high computational performance of the method, ulisse appears to be a promising tool for selecting various types of objects in current and future wide-field surveys (e.g., Euclid, LSST etc.) that target millions of sources every single night. For future work, the application of explainable artificial intelligence algorithms Goebel et al. (2018) might provide new insights into which of the features are most relevant for AGN detection, and may allow us to gain new insight into which observables better trace the physical properties of the sources under investigation.

We participated in the LSST AGN Data Challenge6 (Yu & Richards 2021) which is part of the LSST Enabling Science Program Awards7. The dataset included sources coming from two main survey regions: SDSS Stripe 82 (S82), and XMM-LSS8. The challenge did not provide a single specific task (although all are specifically tuned to AGN selection and characterization) and the participants were free to address any possible AGN-related problem. We decided to apply UL SSE to the detection of AGN in this specific dataset as well and came second place in the competition9. Although most experiments in the Data Challenge focused on Machine Learning applications, as each team was free to address any AGN-related problem, it is difficult to make a fair comparison between the different results. For instance, Savic et al. (in prep.) used support vector machines, random forests, and extreme gradient boosting, reaching classifying accuracies of >98%, which are far higher than ours. On the other hand, when using deep artificial neural networks that utilize pixel-level information, Savic and collaborators did not observe any improvement. However, there are two main differences in these approaches: first, all these methods used tabulated (astrometric, photometric, color, morphological and variability) features, thus requiring a preliminary feature extraction (and thus optimization) phase, while ulisse works directly on images without any pre-processing steps. Second, the data challenge dataset was different from the one discussed here, and heavily skewed toward quasar-like sources and bright AGNs; in this work we extended the method to a more general dataset of low-luminosity AGNs with well-resolved host-galaxy features. Thus, these approaches should be considered complementary, and their use tailored to the specific scientific goal in mind.

Acknowledgements

We acknowledge support from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 721463 to the SUNDIAL Innovative Training Networks. L.D., R.S. and P.M.-N. acknowledge support from research grant 200021_192285 ‘Image data validation for AI systems’ funded by the Swiss National Science Foundation (SNSF). The work of O.T. was supported by the research grant number 2017W4HA7S ‘NAT-NET: Neutrino and Astroparticle Theory Network’ under the program PRIN 2017 funded by the Italian Ministero dell’Università e della Ricerca (MUR). M.P. and O.T. also acknowledge financial support from the agreement ASI-INAF no. 2017-14-H.O. M.B. acknowledges financial contributions from the agreement ASI/INAF 2018-23-HH.0, Euclid ESA mission – Phase D. The authors would like to thank the anonymous referee for the comments and suggestions which helped us to improve the paper.

Appendix A Fractions of different object classes by distance for AGN and nonAGN prototypes obtained by ulisse

Table A.1

Obtained results for AGN prototypes #1-4 presented in Table 2.

Table A.2

Obtained results for AGN prototypes #5-8 presented in Table 2.

Table A.3

Obtained results for nonAGN prototypes #9-13 presented in Table 3.

Table A.4

Results for AGN prototypes #2,3, and 6 obtained by our method based on one single g, r or i-band in comparison with the results obtained based on three bands.

Table A.5

Application of the recursive technique to our method on the example of prototype #2.

Appendix B Neighbors

In this section, we show the 25 nearest neighbors for the 13 prototypes used in this work.

thumbnail Fig. B.1

Closest 25 neighbors for AGN prototype #1.
thumbnail Fig. B.2

Closest 25 neighbors for AGN prototype #2.
thumbnail Fig. B.3

Closest 25 neighbors for AGN prototype #3.
thumbnail Fig. B.4

Closest 25 neighbors for AGN prototype #4.
thumbnail Fig. B.5

Closest 25 neighbors for AGN prototype #5.
thumbnail Fig. B.6

Closest 25 neighbors for AGN prototype #6.
thumbnail Fig. B.7

Closest 25 neighbors for AGN prototype #7.
thumbnail Fig. B.8

Closest 25 neighbors for AGN prototype #8.
thumbnail Fig. B.9

Closest 25 neighbors for nonAGN prototype #9.
thumbnail Fig. B.10

Closest 25 neighbors for nonAGN prototype #10.
thumbnail Fig. B.11

Closest 25 neighbors for nonAGN prototype#11.
thumbnail Fig. B.12

Closest 25 neighbors for nonAGN prototype #12.
thumbnail Fig. B.13

Closest 25 neighbors for nonAGN prototype #13.

References

  1. Agostino, C.J., & Salim, S. 2019, ApJ, 876, 12 [NASA ADS] [CrossRef] [Google Scholar]
  2. Ahumada, R., Prieto, C.A., Almeida, A., et al. 2020, ApJS, 249, 3 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aihara, H., AlSayyad, Y., Ando, M., et al. 2019, PASJ, 71, 114 [Google Scholar]
  4. Álvarez-Márquez, J., Colina, L., Marques-Chaves, R., et al. 2019, A&A, 629, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Awang Iskandar, D.N.F., Zijlstra, A.A., McDonald, I., et al. 2020, Galaxies, 8, 88 [NASA ADS] [CrossRef] [Google Scholar]
  6. Baldwin, J.A., Phillips, M.M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [Google Scholar]
  7. Baron, D. 2019, ArXiv e-prints [arXiv:1904.07248] [Google Scholar]
  8. Baron, D., & Poznanski, D. 2017, MNRAS, 465, 4530 [NASA ADS] [CrossRef] [Google Scholar]
  9. Birchall, K.L., Watson, M.G., & Aird, J. 2020, MNRAS, 492, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bishop, C.M. 2006, Pattern Recognition and Machine Learning (Springer) [Google Scholar]
  11. Blanton, M.R., Bershady, M.A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brandt, W., & Hasinger, G. 2005, ArA&A, 43, 827 [NASA ADS] [CrossRef] [Google Scholar]
  13. Brescia, M., Cavuoti, S., D’Abrusco, R., Longo, G., & Mercurio, A. 2013, ApJ, 772, 140 [NASA ADS] [CrossRef] [Google Scholar]
  14. Brescia, M., Salvato, M., Cavuoti, S., et al. 2019, MNRAS, 489, 663 [NASA ADS] [CrossRef] [Google Scholar]
  15. Brinchmann, J., Charlot, S., White, S., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
  16. Byrne, L., Christensen, C., Tsekitsidis, M., Brooks, A., & Quinn, T. 2019, ApJ, 871, 213 [NASA ADS] [CrossRef] [Google Scholar]
  17. Castro-Ginard, A., Jordi, C., Luri, X., et al. 2018, A&A, 618, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Cavuoti, S., Brescia, M., D’Abrusco, R., Longo, G., & Paolillo, M. 2013, MNRAS, 437, 968 [Google Scholar]
  19. Chang, Y.-Y., Hsieh, B.-C., Wang, W.-H., et al. 2021, ApJ, 920, 68 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chen, Y.C. 2021, ApJS, 256, 34 [NASA ADS] [CrossRef] [Google Scholar]
  21. Chung, S.M., Kochanek, C.S., Assef, R., et al. 2014, ApJ, 790, 54 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dark Energy Survey Collaboration, Abbott, T., Abdalla, F.B., et al. 2016, MNRAS, 460, 1270 [NASA ADS] [CrossRef] [Google Scholar]
  23. De Cicco, D., Bauer, F., Paolillo, M., et al. 2021, A&A, 645, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. de Jong, J.T.A., Verdoes Kleijn, G.A., Boxhoorn, D.R., et al. 2015, A&A, 582, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Delli Veneri, M., Cavuoti, S., Brescia, M., Longo, G., & Riccio, G. 2019, MNRAS, 486, 1377 [Google Scholar]
  26. Deng, J., Dong, W., Socher, R., et al. 2009, in 2009 IEEE conference on computer vision and pattern recognition (IEEE), 248 [CrossRef] [Google Scholar]
  27. Ding, Y., Sohn, J.H., Kawczynski, M.G., et al. 2019, Radiology, 290, 456 [CrossRef] [Google Scholar]
  28. D’Isanto, A., & Polsterer, K.L. 2018, A&A, 609, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. D’Isanto, A., Cavuoti, S., Brescia, M., et al. 2016, MNRAS, 457, 3119 [CrossRef] [Google Scholar]
  30. D’Isanto, A., Cavuoti, S., Gieseke, F., & Polsterer, K.L. 2018, A&A, 616, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Eisenstein, D.J., Weinberg, D.H., Agol, E., et al. 2011, AJ, 142, 72 [NASA ADS] [CrossRef] [Google Scholar]
  32. Esteva, A., Kuprel, B., Novoa, R.A., et al. 2017, Nature, 542, 115 [CrossRef] [Google Scholar]
  33. Euclid Collaboration (Desprez, G., et al.) 2020, A&A, 644, A31 [EDP Sciences] [Google Scholar]
  34. Fabian, A.C. 2012, ARA&A, 50, 455 [CrossRef] [Google Scholar]
  35. Faisst, A., Prakash, A., Capak, P., & Lee, B. 2019, ApJL, 881 [Google Scholar]
  36. Falocco, S., Carrera, F.J., & Larsson, J. 2022, MNRAS, 510, 161 [Google Scholar]
  37. Fluke, C.J., & Jacobs, C. 2020, WIREs Data Mining Knowl. Discov., 10, e1349 [CrossRef] [Google Scholar]
  38. Fotopoulou, S., & Paltani, S. 2018, A&A, 619, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Frontera-Pons, J., Sureau, F., Bobin, J., & Le Floch, E. 2017, A&A, 603, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Goebel, R., Chander, A., Holzinger, K., et al. 2018, in Machine Learning and Knowledge Extraction, eds. A. Holzinger, P. Kieseberg, A.M. Tjoa, & E. Weippl (Cham: Springer International Publishing), 295 [CrossRef] [Google Scholar]
  41. Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (MIT Press), http://www.deeplearningbook.org [Google Scholar]
  42. Goudfrooij, P. 1995, PASP, 107, 502 [NASA ADS] [CrossRef] [Google Scholar]
  43. Green, J., Schechter, P., Baltay, C., et al. 2012, ArXiv e-prints [arXiv:1208.4012] [Google Scholar]
  44. Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [Google Scholar]
  45. Hastie, T., Tibshirani, R., Friedman, J.H., & Friedman, J.H. 2009, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2 (Springer) [Google Scholar]
  46. Heckman, T.M., 1980, A&A, 87, 152 [NASA ADS] [Google Scholar]
  47. Heckman, T.M., & Best, P.N. 2014, ARA&A, 52, 589 [NASA ADS] [CrossRef] [Google Scholar]
  48. Heinis, S., Gezari, S., Kumar, S., et al. 2016, ApJ, 826, 62 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hickox, R.C., & Alexander, D.M. 2018, ARA&A, 56, 625 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hirashita, H., Nozawa, T., Villaume, A., & Srinivasan, S. 2015, MNRAS, 454, 1620 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ivezic, Z., Kahn, S.M., Tyson, J.A., et al. 2019, ApJ, 873, 111 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ji, Z., Giavalisco, M., Kirkpatrick, A., et al. 2022, ApJ, 925, 74 [NASA ADS] [CrossRef] [Google Scholar]
  53. Kauffmann, G., Heckman, T.M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [NASA ADS] [CrossRef] [Google Scholar]
  54. Kewley, L.J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kim, D.-W., Protopapas, P., Byun, Y.-I., et al. 2011, ApJ, 735, 68 [NASA ADS] [CrossRef] [Google Scholar]
  56. Kim, Y.J., Bae, J.P., Chung, J.-W., et al. 2021, Sci. Rep., 11, 3605 [NASA ADS] [CrossRef] [Google Scholar]
  57. Kinson, D.A., Oliveira, J.M., & van Loon, J.T. 2021, MNRAS, 507, 5106 [NASA ADS] [CrossRef] [Google Scholar]
  58. Kormendy, J., & Ho, L.C. 2013, ARA&A, 51, 511 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lecun, Y., Bottou, L., Bengio, Y., & Haffner, P. 1998, Proc. IEEE, 86, 2278 [Google Scholar]
  60. Lianou, S., Barmby, P., Mosenkov, A.A., Lehnert, M., & Karczewski, O. 2019, A&A, 631, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Longo, G., Merényi, E., & Tino, P. 2019, PASP, 131, 100101 [NASA ADS] [CrossRef] [Google Scholar]
  62. Lutz, D., Mainieri, V., Rafferty, D., et al. 2010, ApJ, 712, 1287 [NASA ADS] [CrossRef] [Google Scholar]
  63. Magnier, E.A., Schlafly, E.F., Finkbeiner, D.P., et al. 2020, ApJS, 251, 6 [NASA ADS] [CrossRef] [Google Scholar]
  64. Martinazzo, A., Espadoto, M., & Hirata, N.S. 2021, in 2020 25th International Conference on Pattern Recognition (ICPR), IEEE, 4176 [CrossRef] [Google Scholar]
  65. Masters, D., Capak, P., Stern, D., et al. 2015, ApJ, 813, 53 [Google Scholar]
  66. Mateos, S., Alonso-Herrero, A., Carrera, F.J., et al. 2012, MNRAS, 426, 3271 [NASA ADS] [CrossRef] [Google Scholar]
  67. McConnell, N.J., & Ma, C.-P. 2013, ApJ, 764, 184 [NASA ADS] [CrossRef] [Google Scholar]
  68. McCulloch, W.S., & Pitts, W. 1943, Bull. Math. Biophys., 5, 115 [CrossRef] [Google Scholar]
  69. Mendez, A.J., Coil, A.L., Aird, J., et al. 2013, ApJ, 770, 40 [NASA ADS] [CrossRef] [Google Scholar]
  70. Menegola, A., Fornaciali, M., Pires, R., et al. 2017, in 2017 IEEE 14th international symposium on biomedical imaging (ISBI 2017), IEEE, 297 [CrossRef] [Google Scholar]
  71. Merloni, A. 2016, in Astrophysical Black Holes, eds. F. Haardt, V. Gorini, U. Moschella, A. Treves, & M. Colpi (Cham: Springer International Publishing), 101 [NASA ADS] [CrossRef] [Google Scholar]
  72. Mislis, D., Pyrzas, S., & Alsubai, K.A. 2018, MNRAS, 481, 1624 [NASA ADS] [CrossRef] [Google Scholar]
  73. Mullaney, J.R., Pannella, M., Daddi, E., et al. 2012, MNRAS, 419, 95 [NASA ADS] [CrossRef] [Google Scholar]
  74. Ofman, L., Averbuch, A., Shliselberg, A., et al. 2022, New A, 91, 101693 [NASA ADS] [CrossRef] [Google Scholar]
  75. Palaversa, L., Ivezic, Z., Eyer, L., et al. 2013, AJ, 146, 101 [CrossRef] [Google Scholar]
  76. Pan, S.J., & Yang, Q. 2009, IEEE Trans. Knowl. Data Eng., 22, 1345 [Google Scholar]
  77. Prima, B., & Bouhorma, M. 2020, ISPRS, 4443, 343 [NASA ADS] [Google Scholar]
  78. Razim, O., Cavuoti, S., Brescia, M., et al. 2021, MNRAS, 507, 5034 [NASA ADS] [CrossRef] [Google Scholar]
  79. Richards, G.T., Fan, X., Newberg, H.J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
  80. Richards, G.T., Croom, S.M., Anderson, S.F., et al. 2005, MNRAS, 360, 839 [NASA ADS] [CrossRef] [Google Scholar]
  81. Rosario, D.J., Santini, P., Lutz, D., et al. 2013, ApJ, 771, 63 [NASA ADS] [CrossRef] [Google Scholar]
  82. Rosen, S.R., Webb, N.A., Watson, M.G., et al. 2016, A&A, 590, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Rosenblatt, F. 1958, Psychol. Rev., 65 [Google Scholar]
  84. Scaramella, R., Amiaux, J., Mellier, Y., et al. 2022, A&A, 662, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Schaefer, C., Geiger, M., Kuntzer, T., & Kneib, J.-P. 2018, A&A, 611, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Schmidhuber, J. 2015, Neural Netw., 61, 85 [CrossRef] [Google Scholar]
  87. Schmidt, S.J., Malz, A.I., Soo, J.Y.H., et al. 2020, MNRAS, 499, 1587 [NASA ADS] [Google Scholar]
  88. Schneider, D.P., Hall, P.B., Richards, G.T., et al. 2007, AJ, 134, 102 [NASA ADS] [CrossRef] [Google Scholar]
  89. Schneider, D.P., Richards, G.T., Hall, P.B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
  90. Shakura, N.I., & Sunyaev, R.A. 1973, A&A, 24, 337 [Google Scholar]
  91. Shimizu, T.T., Mushotzky, R.F., Meléndez, M., Koss, M., & Rosario, D.J. 2015, MNRAS, 452, 1841 [NASA ADS] [CrossRef] [Google Scholar]
  92. Stein, G., Blaum, J., Harrington, P., Medan, T., & Lukic, Z. 2022, ApJ, 932, 107 [NASA ADS] [CrossRef] [Google Scholar]
  93. Stemo, A., Comerford, J.M., Barrows, R.S., et al. 2020, ApJ, 888, 78 [NASA ADS] [CrossRef] [Google Scholar]
  94. Sánchez-Sáez, P., Lira, P., Cartier, R., et al. 2019, ApJS, 242 [Google Scholar]
  95. Tan, M., & Le, Q. 2019, in International Conference on Machine Learning, PMLR, 6105 [Google Scholar]
  96. Thacker, R.J., MacMackin, C., Wurster, J., & Hobbs, A. 2014, MNRAS, 443, 1125 [NASA ADS] [CrossRef] [Google Scholar]
  97. Thom, C., Tumlinson, J., Werk, J.K., et al. 2012, ApJ, 758, L41 [NASA ADS] [CrossRef] [Google Scholar]
  98. Thomas, D., Maraston, C., & Bender, R. 2002, Ap&SS, 281, 371 [NASA ADS] [CrossRef] [Google Scholar]
  99. Torbaniuk, O., Paolillo, M., Carrera, F., et al. 2021, MNRAS, 506, 2619 [NASA ADS] [CrossRef] [Google Scholar]
  100. Trump, J.R., Konidaris, N.P., Barro, G., et al. 2013, ApJ, 763, L6 [NASA ADS] [CrossRef] [Google Scholar]
  101. Wang, Y., Yao, Q., Kwok, J.T., & Ni, L.M. 2020, ACM Comput. Surv. (CSUR), 53, 1 [Google Scholar]
  102. Weir, N., Fayyad, U.M., & Djorgovski, S. 1995, AJ, 109, 2401 [NASA ADS] [CrossRef] [Google Scholar]
  103. Wenzl, L., Schindler, J.-T., Fan, X., et al. 2021, AJ, 162, 72 [NASA ADS] [CrossRef] [Google Scholar]
  104. York, D.G., Adelman, J., Anderson, J.E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  105. Yu, W., & Richards, G. 2021, LSSTC AGN Data Challenge, https://github.com/RichardsGroup/AGN_DataChallenge [CrossRef] [Google Scholar]
  106. Zhang, K., & Hao, L. 2018, ApJ, 856, 171 [NASA ADS] [CrossRef] [Google Scholar]
  107. Zou, M., & Zhong, Y. 2018, Sens. Imaging, 19, 6 [NASA ADS] [CrossRef] [Google Scholar]
1

An example notebook is provided at https://github.com/LarsDoorenbos/ulisse

5

The NVIDIA GeForce™ RTX 2060 is powered by the Turing architecture and has 1920 Cuda Cores, 6GB of RAM, and it is capable of 7.2 TFLOPS, for further details see: https://www.nvidia.com/en-me/geforce/graphics-cards/rtx-2060/

All Tables

Table 1

Summary of the different datasets studied in this work.

In the text
Table 2

Summary of the thumbnails used as AGN prototypes in our work.

In the text
Table 3

Overview of the thumbnails used as nonAGN prototypes in our work.

In the text
Table 4

Fractions of SFG, Composite, AGN, and Unclassified objects for each of the 13 prototypes over their 300 nearest neighbors.

In the text
Table 5

Fractions of SFG, Composite, AGN, and Unclassified objects for each of the 13 prototypes over their 300 closest neighbors obtained based on a single band SDSS image (g, r or i band).

In the text
Table 6

Results obtained after five iterations of the recursive application of ulisse with n = 25.

In the text
Table A.1

Obtained results for AGN prototypes #1-4 presented in Table 2.

In the text
Table A.2

Obtained results for AGN prototypes #5-8 presented in Table 2.

In the text
Table A.3

Obtained results for nonAGN prototypes #9-13 presented in Table 3.

In the text
Table A.4

Results for AGN prototypes #2,3, and 6 obtained by our method based on one single g, r or i-band in comparison with the results obtained based on three bands.

In the text
Table A.5

Application of the recursive technique to our method on the example of prototype #2.

In the text

All Figures

thumbnail Fig. 1

Three objects in our sample which most strongly activate features 11, 41, 541, 835, and 1073 (arbitrarily chosen for visualization), together with their feature maps. We provide these for all 1280 features at http://dame.na.astro.it/ulisse.
In the text
thumbnail Fig. 2

Overview of ulisse.
In the text
thumbnail Fig. B.1

Closest 25 neighbors for AGN prototype #1.
In the text
thumbnail Fig. B.2

Closest 25 neighbors for AGN prototype #2.
In the text
thumbnail Fig. B.3

Closest 25 neighbors for AGN prototype #3.
In the text
thumbnail Fig. B.4

Closest 25 neighbors for AGN prototype #4.
In the text
thumbnail Fig. B.5

Closest 25 neighbors for AGN prototype #5.
In the text
thumbnail Fig. B.6

Closest 25 neighbors for AGN prototype #6.
In the text
thumbnail Fig. B.7

Closest 25 neighbors for AGN prototype #7.
In the text
thumbnail Fig. B.8

Closest 25 neighbors for AGN prototype #8.
In the text
thumbnail Fig. B.9

Closest 25 neighbors for nonAGN prototype #9.
In the text
thumbnail Fig. B.10

Closest 25 neighbors for nonAGN prototype #10.
In the text
thumbnail Fig. B.11

Closest 25 neighbors for nonAGN prototype#11.
In the text
thumbnail Fig. B.12

Closest 25 neighbors for nonAGN prototype #12.
In the text
thumbnail Fig. B.13

Closest 25 neighbors for nonAGN prototype #13.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.