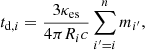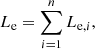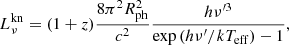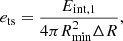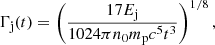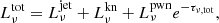| Issue |
A&A
Volume 654, October 2021
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202141325 | |
| Published online | 21 October 2021 | |
Does a long-lived remnant neutron star exist after short gamma-ray burst GRB 160821B?
1
Institute of Astrophysics, Central China Normal University, Wuhan 430079, PR China
e-mail: yuyw@mail.ccnu.edu.cn
2
Key Laboratory of Quark and Lepton Physics (Central China Normal University), Ministry of Education, Wuhan 430079, PR China
3
Department of Astronomy, School of Physics, Peking University, Beijing 100871, PR China
Received:
17
May
2021
Accepted:
6
August
2021
Mergers of double neutron stars (DNSs) could lead to the formation of a long-lived massive remnant NS, which has been previously suggested to explain the AT 2017gfo kilonova emission in the famous GW170817 event. For an NS-affected kilonova, it is expected that a nonthermal emission component can be contributed by a pulsar wind nebula (PWN), which results from the interaction of the wind from the remnant NS with the preceding merger ejecta. Therefore, the discovery of such a nonthermal PWN emission would provide evidence for the existence of the remnant NS. Similar to GRB 170817A, GRB 160821B is also one of the nearest short gamma-ray bursts (SGRBs). A candidate kilonova is widely believed to appear in the ultraviolet–optical–infrared afterglows of GRB 160821B. Here, by modeling the afterglow light curves and spectra of GRB 160821B, we find that invoking nonthermal PWN emission can indeed be highly consistent with the observational data. This may indicate that the formation of a stable massive NS is not uncommon in DNS merger events, and therefore that the equation of state of the post-merger NSs should be stiff enough.
Key words: gravitational waves / gamma-ray burst: individual: GRB 160821B / stars: neutron / pulsars: general
© ESO 2021
1. Introduction
Mergers of double neutron stars (DNSs) and black hole–neutron star binaries are important sources of gravitational waves (GWs) for aLIGO/Virgo and other ground-based GW detectors. After a merger, a pair of collimated relativistic jets could be launched to generate a short-duration gamma-ray burst (SGRB) through the internal dissipations in the jet (Paczynski 1986; Eichler et al. 1989; Narayan et al. 1992; Nakar 2007). The SGRB can be observed if the jet axis does not deviate too much away from the direction of Earth (Rezzolla et al. 2011; Paschalidis et al. 2015). The interaction of the jet with the ambient interstellar medium can drive an external shock (ES) to produce long-lasting broadband afterglows (Rees & Meszaros 1992; Mészáros & Rees 1997; Sari et al. 1998; Chevalier & Li 2000; Granot & Sari 2002). Accompanying the jet launching, a nonrelativistic mass of ∼10−4 − 10−2 M⊙ can be ejected more widely due to the effects of tidal disruption, collision squeeze, and accretion feedback. It is suggested that nearly half of the elements heavier than iron in the Universe can be synthesized in these neutron-rich merger ejecta, through the rapid neutron-capture process (r-process; Lattimer & Schramm 1974, 1976; Symbalisty & Schramm 1982). Then, the radioactive decays of the r-process elements can effectively heat the ejecta to generate a bright thermal emission, which was first predicted by Li & Paczyński (1998) and subsequently by Metzger et al. (2010). This transient thermal emission is now usually termed “kilonova”, because its peak luminosity is expected to be a few thousand times that of the typical nova phenomena (Roberts et al. 2011; Barnes & Kasen 2013; Kasen et al. 2013, 2015, 2017; Tanaka & Hotokezaka 2013; Yu et al. 2013; Grossman et al. 2014; Metzger & Piro 2014; Metzger & Fernández 2014; Wanajo et al. 2014; Perego et al. 2014; Martin et al. 2015; Li & Yu 2016; Metzger 2017a; Zhu et al. 2020).
The first multi-messenger GW event was discovered on 17 August, 2017. About 1.7 s after the GW170817 signal detected by LIGO and Virgo (Abbott et al. 2017a), the Fermi Gamma-ray Burst Monitor was successfully triggered by GRB 170817A (Abbott et al. 2017b; Goldstein et al. 2017; Zhang et al. 2018) and subsequently a large number of follow-up observations monitored the afterglow emission in different electromagnetic bands from the radio to X-rays (Alexander et al. 2017; Hallinan et al. 2017; Margutti et al. 2017; Troja et al. 2017; D’Avanzo et al. 2018; Ghirlanda et al. 2019; Lazzati et al. 2018; Lyman et al. 2018) and the kilonova AT 2017gfo in the ultraviolet–optical–infrared band (Abbott et al. 2017c; Andreoni et al. 2017; Arcavi et al. 2017; Chornock et al. 2017; Coulter et al. 2017; Covino et al. 2017; Cowperthwaite et al. 2017; Evans et al. 2017; Hu et al. 2017; Kilpatrick et al. 2017; Lipunov et al. 2017; Nicholl et al. 2017; Smartt et al. 2017; Soares-Santos et al. 2017; Tanvir et al. 2017). The observations of GRB 170817A and its afterglows robustly confirmed the long-standing hypothesis that SGRBs can originate from compact binary mergers. Moreover, it became possible to explore the angular structure of the SGRB jet from an off-axis view (Lamb & Kobayashi 2017; Granot et al. 2018; Lazzati et al. 2018; Mooley et al. 2018a,b; Li et al. 2019). Meanwhile, the observations of AT 2017gfo indicated the existence of the merger ejecta, which suggests that the progenitor binary should at least contain one NS. In more detail, the existence of a “blue” and possibly also a “purple” component in the AT 2017gfo emission further indicated that the merger product of the GW170817 event is very likely to be a hypermassive NS, which lasted for at least a few hundred milliseconds, as an immediately formed black hole can only be associated with a “red” kilonova1 (Cowperthwaite et al. 2017; Perego et al. 2017; Tanaka et al. 2017; Tanvir et al. 2017; Villar et al. 2017; Kawaguchi et al. 2018). Therefore, in summary, the progenitor of the GW170817 event can be identified as a DNS system, which is consistent with the result of the GW analysis.
However, strictly speaking, in the radioactive power model, the observationally required mass and opacity of the merger ejecta cannot fall in an acceptable parameter region predicted by the merger simulations. Therefore, alternatively, Yu et al. (2018) and Li et al. (2018) modeled the AT 2017gfo emission by invoking a long-lived post-merger NS. Such a remnant NS can naturally provide an extra energy source for the kilonova emission and thus reduce the requirement on the ejecta mass. Simultaneously, the remnant NS can also influence the opacity of the merger ejecta, because of the possible ionization of lanthanides by the hard emission from the NS. About 155 days after GRB 170817A, Piro et al. (2019) discovered a possible X-ray flare, which somewhat implied, independently, the existence of the remnant NS. Furthermore, by considering the interaction between the merger ejecta and the relativistic wind from the remnant NS, it is expected that a nonthermal emission component could be generated by the shocked NS wind (i.e., the pulsar wind nebula; PWN), in addition to the thermal kilonova emission from the merger ejecta (Kotera et al. 2013; Yu et al. 2019). Very encouragingly, such a nonthermal emission component has indeed been resolved from the AT 2017gfo data, as presented in Ren et al. (2019), which can improve the fitting to the AT 2017gfo data significantly.
In view of the ultrahigh mass of the merger product of around 2.5 M⊙, it is undoubtedly necessary and important to further test the existence of post-merger NSs (Gao et al. 2016; Li et al. 2016, 2017; Ai et al. 2018; Zhu et al. 2018; Sarin et al. 2020; Beniamini & Lu 2021), which can provide a robust constraint on the equation of state of the NS matter and then improve our understanding of the low-energy feature of strong interaction. Besides the GRB 170817A/AT 2017gfo event, searches for possible kilonova emission have already been carried out in the afterglows of many SGRBs since 2013 (Berger et al. 2013; Tanvir et al. 2013; Yang et al. 2015; Jin et al. 2015, 2016, 2018, 2020; Gao et al. 2015, 2017; Kasliwal et al. 2017). Among the SGRBs with a kilonova candidate, GRB 160821B has one of the lowest redshifts, of namely z = 0.162. From its optical/near-infrared(NIR) afterglow, an obvious excess was found. Because of its close distance, the kilonova emission associated with GRB 160821B is in principle detectable and can provide a natural explanation for the observed optical/NIR excess (Lamb et al. 2019; Troja et al. 2019). In view of its luminosity, which is lower than that of AT 2017gfo, the kilonova after GRB 160821B can in principle be modeled with a pure radioactive power. However, it could still be necessary to mention that a significant internal plateau appeared in the early X-ray afterglow during the first few hundred seconds (see the insert in Fig. 1), which indicated that a post-merger NS also exists in this event. According to these observations, Ma et al. (2021) suggested that the post-merger NS could collapse into a black hole and then the subsequent kilonova could be powered by the accretion onto the black hole. Nevertheless, alternatively, as suggested by Yu et al. (2018), the steep decay after the internal plateau may not represent the collapse of the NS, but may simply be caused by the suppression of the magnetic dipole radiation of the NS. In this case, the spin-down of the NS of relatively low luminosity can still power the kilonova emission, which can be generally called a mergernovae (Yu et al. 2013). This scenario can provide a natural explanation for the AT 2017gfo emission. Therefore, in our opinion, this situation could also appear in the case of GRB 160821B. This paper is devoted to testing whether or not there is a nonthermal emission component arising from the interaction between the NS wind and the merger ejecta, as mentioned above for AT 2017gfo.
 |
Fig. 1. Multi-wavelength light curves of the afterglow emission of GRB 160821B for different electromagnetic bands as labeled. The observational data are taken from (Lamb et al. 2019; Troja et al. 2019) and Swift. The dotted, dash-dotted, dashed, and solid lines correspond to the emission from the jet external shock, the thermal kilonova, the PWN, and their combination, respectively. The insert shows the early X-ray afterglow plateau, which may indicate the remnant NS could intrinsically be a magnetar before its surface magnetic field is buried. |
2. The model
As a result of the collision of a relativistic NS wind with a preceding ejecta, a termination shock (TS) can be formed in the wind to decelerate the wind material, while the ejecta can be heated by absorbing the radiation from the shocked wind. Such an interaction has been previously studied in some semi-analytical studies of GRBs (Dai 2004; Yu & Dai 2007), superluminous supernovae (Kotera et al. 2013), mergernovae (Ren et al. 2019), and even accretion-induced collapses of white dwarfs (Yu et al. 2019). In this paper we employ the model proposed by Yu et al. (2019) and Ren et al. (2019), which is most relevant to the situation concerned here. Namely, a relativistic wind from a millisecond pulsar is blocked by a low-mass optically thick ejecta.
2.1. The PWN emission
The energy luminosity carried by a NS wind can usually be estimated by the luminosity of magnetic dipole radiation of the NS, which reads
where Bp, Rs, and P are the polar magnetic field strength, radius, and spin period of the NS, respectively, and c is the speed of light. Hereafter, the conventional notation Qx = Q/10x is adopted in cgs units. The temporal evolution of this wind luminosity is determined by the spin-down behavior of the NS, which can be written as
where the initial value of the luminosity Lmd, i is given for an initial spin period Pi. About the temporal index, we can take α = 2 when the spin-down is dominated by the magnetic dipole radiation. On the other hand, the NS rotation could sometimes be primarily decelerated by GW radiation if the NS is deformed with a sufficiently high ellipticity ϵ, which leads to α = 1. For these two different braking effects, the spin-down timescale of the NS can be expressed as
and
respectively, where I is the inertia moment and G is the gravitational constant.
When the relativistic wind drives a TS by colliding with the preceding merger ejecta, a PWN (i.e., the shocked wind region) can be formed between the TS and the merger ejecta. Denoting the bulk Lorentz factor of the unshocked wind as Γw, the internal energy density of the PWN can be expressed in terms of the shock jump condition,
where 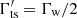 is the Lorentz factor of the TS measured in the rest frame of the injecting unshocked wind,
is the Lorentz factor of the TS measured in the rest frame of the injecting unshocked wind, 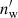 is the comoving number density of the wind electron/positrons, me is the electron rest mass, Rts is the radius of the TS, and the fraction ξ is introduced due to the possible fact that the energy released from the NS is collimated in the jet direction. In our calculations, the value of ets is actually obtained according to the mechanical equilibrium between the PWN and the merger ejecta at the contact discontinuity surface (see Eq. (20)). Then, using Eq. (5), we can reversely obtain the evolution of the TS radius, which is determined by the motion of the inner boundary of the merger ejecta.
is the comoving number density of the wind electron/positrons, me is the electron rest mass, Rts is the radius of the TS, and the fraction ξ is introduced due to the possible fact that the energy released from the NS is collimated in the jet direction. In our calculations, the value of ets is actually obtained according to the mechanical equilibrium between the PWN and the merger ejecta at the contact discontinuity surface (see Eq. (20)). Then, using Eq. (5), we can reversely obtain the evolution of the TS radius, which is determined by the motion of the inner boundary of the merger ejecta.
The electrons and positrons in the PWN can initially be accelerated by the TS to distribute with their random Lorentz factors as dNe/dγ ∝ γ−p for ![$ \gamma\geqslant\gamma_{\rm m}=[(p-2)/(p-1)]\Gamma^\prime_{\rm ts} $](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq8.gif) , where p is a constant spectral index. At time t, the total number of the accelerated electrons can be estimated by
, where p is a constant spectral index. At time t, the total number of the accelerated electrons can be estimated by
Here, we multiply Lmd as a function of time to the time t directly but do not integrate Lmd over t, because the electrons accelerated at early times can be cooled to nonrelativistic very quickly via their synchrotron radiation and sometimes further via synchrotron self-Compton scattering. In order to calculate the synchrotron radiation, we estimate the stochastic magnetic field in the PWN by Bts = (4πϵBets)1/2 with a magnetic equipartition factor ϵB. At the very beginning, the stochastic magnetic field in the PWN could be very high, which can cause the cooling timescale of relativistic electrons (i.e., γ ≳ 2) to be much shorter than the dynamical timescale. In this case, the number of relativistic electrons that can contribute to the synchrotron radiation should be reduced by a fraction of tcol/t, which yields
where 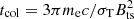 is taken for γ ∼ 2 and σT is the Thomson cross-section.
is taken for γ ∼ 2 and σT is the Thomson cross-section.
Following Sari et al. (1998), we can analytically calculate the synchrotron radiation spectrum of relativistic electrons by
where the peak luminosity is given by 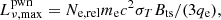 where qe is the electron charge. For the braking frequencies and the spectral index, we have νl = min[νm, νc], νh = max[νm, νc], and q = 2 for νc < νm and q = p for νc > νm, where
where qe is the electron charge. For the braking frequencies and the spectral index, we have νl = min[νm, νc], νh = max[νm, νc], and q = 2 for νc < νm and q = p for νc > νm, where 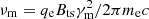 ,
, 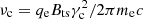 , and the cooling Lorentz factor is defined as
, and the cooling Lorentz factor is defined as ![$ \gamma_{\rm c} = \max[2, 6\pi m_ec/\sigma_{\rm T}B_{\rm ts}^2t] $](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq16.gif) .
.
2.2. The kilonova emission
For the merger ejecta, as usual, we take a power-law density profile as (Nagakura et al. 2014)
with a distribution index of δ, where Mej is the total mass of the ejecta, and Rmin and Rmax are the minimum and maximum radii, respectively. As the internal energy of the ejecta is usually much smaller than its kinetic energy, we assume that the ejecta expand homologously. Therefore, the maximum and minimum ejecta radii for a given time t can be expressed as Rmax = vmaxt and Rmin = vmint, by invoking the maximum and minimum velocities. Following Metzger (2017a), we separate the merger ejecta into n mass layers and denote the layers by the subscript i = 1, 2, …, n, where i = 1 and n represent the bottom and the head layers, respectively. Then, the evolution of the internal energy Eint,i of the ith layer can be determined by the energy conservation law as (Kasen & Bildsten 2010)
where Lh, i is the heating rate due to the absorption of the PWN emission by the layer, 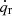 is the radioactive power per unit mass, ηth is the thermalization efficiency of the radioactive power, mi and Ri are the mass and radius of the layer, and Le, i is the observed luminosity contributed by this layer. The specific expressions of the terms in Eq. (10) would be introduced as follows.
is the radioactive power per unit mass, ηth is the thermalization efficiency of the radioactive power, mi and Ri are the mass and radius of the layer, and Le, i is the observed luminosity contributed by this layer. The specific expressions of the terms in Eq. (10) would be introduced as follows.
First of all, the energy injection rate from the PWN to the ith layer can be calculated by
where the value of 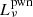 is given by Eq. (8) and the optical depths are defined as
is given by Eq. (8) and the optical depths are defined as
and
When n → ∞ and thus Δτi → 0, we obtain 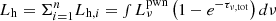 from Eq. (11), where τν,tot is the optical depth of the whole ejecta for a given frequency. In our calculations, Eq. (17) in Yu et al. (2019) is adopted to describe the frequency-dependent opacity κν, which was obtained by fitting the numerical results presented in Fig. 8 of Kotera et al. (2013). Secondly, the radioactive power per unit mass reads (Korobkin et al. 2012)
from Eq. (11), where τν,tot is the optical depth of the whole ejecta for a given frequency. In our calculations, Eq. (17) in Yu et al. (2019) is adopted to describe the frequency-dependent opacity κν, which was obtained by fitting the numerical results presented in Fig. 8 of Kotera et al. (2013). Secondly, the radioactive power per unit mass reads (Korobkin et al. 2012)
where t0 = 1.3 s and σ = 0.11 s, and the thermalization efficiency is given by (Barnes et al. 2016; Metzger 2017b)
where tday = t/day. Thirdly, the luminosity of the thermal emission of the ith layer can be determined by the radiative diffusion as
where the radiation diffusion timescale of the ith layer is
where κes = 0.2 cm2 g−1 is the electron-scattering opacity because the ejecta thermal emission is mainly in the UV/optical bands. Under this treatment, the propagation of the PWN emission in the ejecta and the radiative transfer of the ejecta heat can be generally described by a set of independent equations for different layers.
After the calculations of all layers, we can finally obtain the total luminosity of the ejecta thermal emission as
which corresponds to a black-body temperature of 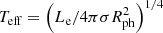 , where σ is the Stephan-Boltzmann constant, and Rph is the photosphere radius where the electron-scattering optical depth satisfies (τes, tot − τes,i)=1. If Rph < Rmin, we simply set Rph = Rmin. For an effective black-body spectrum, the luminosity of the kilonova emission at a frequency ν can be given by
, where σ is the Stephan-Boltzmann constant, and Rph is the photosphere radius where the electron-scattering optical depth satisfies (τes, tot − τes,i)=1. If Rph < Rmin, we simply set Rph = Rmin. For an effective black-body spectrum, the luminosity of the kilonova emission at a frequency ν can be given by
where h is the Planck constant, k is the Boltzmann constant, and ν′=(1 + z)ν. Meanwhile, using the internal energy of the innermost layer Eint,1 and according to the mechanical equilibrium between the PWN and the merger ejecta, we can obtain the internal energy density of the PWN by
where ΔR = (Rmax − Rmin)/n. We can then finally combine the calculations for the PWN emission and the kilonova.
2.3. The jet ES emission
The multi-wavelength afterglows of GRB 160821B must be primarily contributed by the ES driven by the GRB jet decelerating into the interstellar medium. In principle, the relativistic wind from the remnant NS can also interact with the GRB jet and thus influence the emission of the ES, which can be described by the model of Dai (2004) and Yu & Dai (2007). Nevertheless, by considering that the wind luminosity is probably only comparable to the luminosity of the kilonova, the influence of the NS wind on the jet ES can be neglected in the case of GRB 160821B, unless the wind energy is extremely highly collimated in the jet direction (i.e., ξ ≪ 1). Therefore, we simply employ the standard ES model introduced in Sari et al. (1998) and Huang et al. (2000), Huang & Cheng (2003). In short, while the dynamical evolution of the jet is described by the classical formula as
the synchrotron luminosity 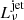 of the ES emission can also be determined using Eq. (8) for corresponding parameters and characteristic quantities. Here, Γj and Ej are the Lorentz factor and the isotropically equivalent kinetic energy of the jet, n0 is the particle number density of the medium, and mp is the mass of proton. A half-opening angle θj of the jet is taken in our calculation. When the Lorentz factor of the jet decreases to be smaller than
of the ES emission can also be determined using Eq. (8) for corresponding parameters and characteristic quantities. Here, Γj and Ej are the Lorentz factor and the isotropically equivalent kinetic energy of the jet, n0 is the particle number density of the medium, and mp is the mass of proton. A half-opening angle θj of the jet is taken in our calculation. When the Lorentz factor of the jet decreases to be smaller than 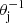 , the analytical results given by Eq. (8) should be further multiplied by an extra suppression factor (Γjθj)−2, which is called a jet break. Sometimes, the Newtonian effect should also be taken into account.
, the analytical results given by Eq. (8) should be further multiplied by an extra suppression factor (Γjθj)−2, which is called a jet break. Sometimes, the Newtonian effect should also be taken into account.
3. Comparison with the GRB 160821B observations
As described, the electromagnetic emission after a DNS merger is contributed by three components as
which can be used to fit the multi-wavelength afterglow emission of GRB 160821B. In view of the limited number of the afterglow data, in this paper we do not seek a complete constraint on the model parameters. Alternatively, we simply try to test the compatibility of the model with the observations. Tentative modelings of the light curves and spectra are presented in Figs. 1 and 2, respectively. The used parameter values are listed in Table 1, which are all typical for SGRBs including GRB 170817A. Specifically, the X-ray afterglow for t > 103 s can be easily accounted for by the emission from the jet ES, which was not influenced by the energy release from the remnant NS because of the huge kinetic energy of the jet. Moreover, a jet break could happen a few days after GRB 160821B. It should also be mentioned that the very early plateau in the X-ray afterglow has not been modeled. This plateau can probably be attributed to the PWN emission at the jet direction before the surface magnetic field of the NS was buried (see Yu et al. 2018 and Li et al. 2021 for related discussions). Secondly, for the radio afterglow, the upper limit appearing at t ∼ 1 day indicated that the two observational data could not have the same origin, as previously suggested by Troja et al. (2019) and Lamb et al. (2019). Then, while the late data at ∼10 days is ascribed to the ES emission, the early data at ∼0.1 days is probably contributed by another emission region; for example, a reverse shock propagating into the GRB jet (Troja et al. 2019). Finally, for the optical/NIR data, by subtracting the contribution from the jet ES, we can naturally attribute the excesses to the kilonova and PWN emission.
 |
Fig. 2. Ultraviolet–optical–infrared spectra of the afterglow emission of GRB 160821B for different times as labeled. The observational data are taken from (Lamb et al. 2019; Troja et al. 2019). The dotted, dash-dotted, dashed, and solid lines correspond to the emissions of the jet external shock, the thermal kilonova, the PWN, and their combination, respectively. |
Adopted parameter values for the tentative fitting of the observations of GRB 160821B.
In more detail, the peak time of the kilonova emission is found to be around ∼1 day, which can be naturally explained by the diffusion timescale of tp = (κesMej/4πvejc)1/2 for a typical ejecta mass of Mej ∼ 0.01 M⊙ and a typical electron-scattering opacity of κes ∼ 0.2 cm2 g−1. Although a large number of lanthanides are believed to be synthesized in the merger ejecta, the required small opacity can still be understood by considering that the merger ejecta could be deeply ionized by the early PWN emission before the surface magnetic field of the NS is suppressed. The radioactive power corresponding to the ejecta mass Mej ∼ 0.01 M⊙ can be comparable to the emission luminosity of the PWN. This indicates that the kilonova emission after GRB 160821B was powered by hybrid energy sources, which mirrors the situation for AT 2017gfo (Yu et al. 2018). In any case, the crucial effect of the remnant NS is mainly displayed in the appearance of the nonthermal PWN emission, which can help to explain the relatively slow decay of the excess emission. Such nonthermal PWN emission can also be clearly seen from the evolving spectra presented in Fig. 2. As shown, while the thermal component shifts quickly from the UV to the IR, the synchrotron emission from the PWN gradually increases to be dominated about 10 days after GRB 160821B.
4. Summary
It is of fundamental importance to determine the nature of the merger product of DNSs. The existence of a long-lived remnant NS can leave many imprints in the kilonova emission after the GW event by reducing the opacity of the merger ejecta, providing an energy injection for the thermal kilonova emission, and in particular contributing a nonthermal emission by the PWN as a result of the interaction between the pulsar wind and the merger ejecta. Such a situation has previously been suggested to appear in the GRB 170817A/AT 2017gfo event. In the present paper, by resolving the nonthermal PWN emission component from the kilonova data, we further find that the remnant NS scenario can also be consistent with the afterglow emission of GRB 160821B. Although stringent constraint of the model is still difficult to achieve because of the very limited amount of afterglow data, our result nevertheless indicates that the formation of a long-lived massive NS is probably not rare in DNS merger events, which implies that the equation of state of the post-merger NSs should be stiff enough.
Acknowledgments
This work is supported by the National SKA Program of China (grant No. 2020SKA0120300) and the National Natural Science Foundation of China (grant Nos. 11822302 and 11833003).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, ApJ, 848, L13 [CrossRef] [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, Phys. Rev. Lett., 119, 161101 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017c, ApJ, 848, L12 [Google Scholar]
- Ai, S., Gao, H., Dai, Z.-G., et al. 2018, ApJ, 860, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, K. D., Berger, E., Fong, W., et al. 2017, ApJ, 848, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Andreoni, I., Ackley, K., Cooke, J., et al. 2017, PASA, 34 [Google Scholar]
- Arcavi, I., Hosseinzadeh, G., Howell, D. A., et al. 2017, Nature, 551, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Kasen, D. 2013, ApJ, 775, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., Kasen, D., Wu, M.-R., & Martínez-Pinedo, G. 2016, ApJ, 829, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Beniamini, P., & Lu, W. 2021, ApJ, submitted, [arXiv:2104.01181] [Google Scholar]
- Berger, E., Fong, W., & Chornock, R. 2013, ApJ, 774, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Li, Z.-Y. 2000, ApJ, 536, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Chornock, R., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Coulter, D. A., Foley, R. J., Kilpatrick, C. D., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S., Wiersema, K., Fan, Y. Z., et al. 2017, Nat. Astron., 1, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Cowperthwaite, P. S., Berger, E., Villar, V. A., et al. 2017, ApJ, 848, L17 [CrossRef] [Google Scholar]
- Dai, Z. G. 2004, ApJ, 606, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- D’Avanzo, P., Campana, S., Salafia, O. S., et al. 2018, A&A, 613, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichler, D., Livio, M., Piran, T., & Schramm, D. N. 1989, Nature, 340, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Cenko, S. B., Kennea, J. A., et al. 2017, Science, 358, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Ding, X., Wu, X.-F., Dai, Z.-G., & Zhang, B. 2015, ApJ, 807, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Zhang, B., & Lü, H.-J. 2016, Phys. Rev. D, 93, 044065 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Zhang, B., Lü, H.-J., & Li, Y. 2017, ApJ, 837, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Ghirlanda, G., Salafia, O. S., Paragi, Z., et al. 2019, Science, 363, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, ApJ, 848, L14 [CrossRef] [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., Gill, R., Guetta, D., & De Colle, F. 2018, MNRAS, 481, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Grossman, D., Korobkin, O., Rosswog, S., & Piran, T. 2014, MNRAS, 439, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Hallinan, G., Corsi, A., Mooley, K. P., et al. 2017, Science, 358, 1579 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, L., Wu, X., Andreoni, I., et al. 2017, Sci. Bull., 62, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y. F., & Cheng, K. S. 2003, MNRAS, 341, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Y. F., Gou, L. J., Dai, Z. G., & Lu, T. 2000, ApJ, 543, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z.-P., Li, X., Cano, Z., et al. 2015, ApJ, 811, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z.-P., Hotokezaka, K., Li, X., et al. 2016, Nat. Commun., 7, 12898 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z.-P., Li, X., Wang, H., et al. 2018, ApJ, 857, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Jin, Z.-P., Covino, S., Liao, N.-H., et al. 2020, Nat. Astron., 4, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., & Bildsten, L. 2010, ApJ, 717, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Badnell, N. R., & Barnes, J. 2013, ApJ, 774, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Fernández, R., & Metzger, B. D. 2015, MNRAS, 450, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Metzger, B., Barnes, J., Quataert, E., & Ramirez-Ruiz, E. 2017, Nature, 551, 80 [Google Scholar]
- Kasliwal, M. M., Korobkin, O., Lau, R. M., Wollaeger, R., & Fryer, C. L. 2017, ApJ, 843, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Shibata, M., & Tanaka, M. 2018, ApJ, 865, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Kilpatrick, C. D., Foley, R. J., Kasen, D., et al. 2017, Science, 358, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Korobkin, O., Rosswog, S., Arcones, A., & Winteler, C. 2012, MNRAS, 426, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Kotera, K., Phinney, E. S., & Olinto, A. V. 2013, MNRAS, 432, 3228 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, G. P., & Kobayashi, S. 2017, MNRAS, 472, 4953 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, G. P., Tanvir, N. R., Levan, A. J., et al. 2019, ApJ, 883, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Schramm, D. N. 1974, ApJ, 192, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Schramm, D. N. 1976, ApJ, 210, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Lazzati, D., Perna, R., Morsony, B. J., et al. 2018, Phys. Rev. Lett., 120, 241103 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-Z., & Yu, Y.-W. 2016, ApJ, 819, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Zhang, B., Zhang, N.-B., et al. 2016, Phys. Rev. D, 94, 083010 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., Zhu, Z.-Y., & Zhou, X. 2017, ApJ, 844, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-Z., Liu, L.-D., Yu, Y.-W., & Zhang, B. 2018, ApJ, 861, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y.-S., Chen, A., & Yu, Y.-W. 2019, Res. Astron. Astrophys., 19, 115 [Google Scholar]
- Li, S.-Z., Yu, Y.-W., Gao, H., & Zhang, B. 2021, ApJ, 907, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Lipunov, V. M., Gorbovskoy, E., Kornilov, V. G., et al. 2017, ApJ, 850, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Lyman, J. D., Lamb, G. P., Levan, A. J., et al. 2018, Nat. Astron., 2, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, S.-B., Xie, W., Liao, B., et al. 2021, ApJ, 911, 97 [CrossRef] [Google Scholar]
- Margutti, R., Berger, E., Fong, W., et al. 2017, ApJ, 848, L20 [CrossRef] [Google Scholar]
- Martin, D., Perego, A., Arcones, A., et al. 2015, ApJ, 813, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, P., & Rees, M. J. 1997, ApJ, 476, 232 [CrossRef] [Google Scholar]
- Metzger, B. D. 2017a, Liv. Rev. Rel., 20, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D. 2017b, ArXiv e-prints [arXiv:1710.05931] [Google Scholar]
- Metzger, B. D., & Fernández, R. 2014, MNRAS, 441, 3444 [CrossRef] [Google Scholar]
- Metzger, B. D., & Piro, A. L. 2014, MNRAS, 439, 3916 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, B. D., Martínez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Deller, A. T., Gottlieb, O., et al. 2018a, Nature, 561, 355 [Google Scholar]
- Mooley, K. P., Nakar, E., Hotokezaka, K., et al. 2018b, Nature, 554, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Nagakura, H., Hotokezaka, K., Sekiguchi, Y., Shibata, M., & Ioka, K. 2014, ApJ, 784, L28 [CrossRef] [Google Scholar]
- Nakar, E. 2007, Phys. Rep., 442, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Paczynski, B., & Piran, T. 1992, ApJ, 395, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholl, M., Berger, E., Kasen, D., et al. 2017, ApJ, 848, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Paschalidis, V., Ruiz, M., & Shapiro, S. L. 2015, ApJ, 806, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Perego, A., Rosswog, S., Cabezón, R. M., et al. 2014, MNRAS, 443, 3134 [NASA ADS] [CrossRef] [Google Scholar]
- Perego, A., Radice, D., & Bernuzzi, S. 2017, ApJ, 850, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, L., Troja, E., Zhang, B., et al. 2019, MNRAS, 483, 1912 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., & Meszaros, P. 1992, MNRAS, 258, 41 [Google Scholar]
- Ren, J., Lin, D.-B., Zhang, L.-L., et al. 2019, ApJ, 885, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Rezzolla, L., Giacomazzo, B., Baiotti, L., et al. 2011, ApJ, 732, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, L. F., Kasen, D., Lee, W. H., & Ramirez-Ruiz, E. 2011, ApJ, 736, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Narayan, R. 1998, ApJ, 497, L17 [Google Scholar]
- Sarin, N., Lasky, P. D., & Ashton, G. 2020, Phys. Rev. D, 101, 063021 [CrossRef] [Google Scholar]
- Smartt, S. J., Chen, T. W., Jerkstrand, A., et al. 2017, Nature, 551, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Soares-Santos, M., Holz, D. E., Annis, J., et al. 2017, ApJ, 848, L16 [CrossRef] [Google Scholar]
- Symbalisty, E., & Schramm, D. N. 1982, Astrophys. Lett., 22, 143 [NASA ADS] [Google Scholar]
- Tanaka, M., & Hotokezaka, K. 2013, ApJ, 775, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Utsumi, Y., Mazzali, P. A., et al. 2017, PASJ, 69, 102 [NASA ADS] [Google Scholar]
- Tanvir, N. R., Levan, A. J., Fruchter, A. S., et al. 2013, Nature, 500, 547 [CrossRef] [Google Scholar]
- Tanvir, N. R., Levan, A. J., González-Fernández, C., et al. 2017, ApJ, 848, L27 [CrossRef] [Google Scholar]
- Troja, E., Piro, L., van Eerten, H., et al. 2017, Nature, 551, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Troja, E., Castro-Tirado, A. J., Becerra González, J., et al. 2019, MNRAS, 489, 2104 [Google Scholar]
- Villar, V. A., Guillochon, J., Berger, E., et al. 2017, ApJ, 851, L21 [Google Scholar]
- Wanajo, S., Sekiguchi, Y., Nishimura, N., et al. 2014, ApJ, 789, L39 [Google Scholar]
- Yang, B., Jin, Z.-P., Li, X., et al. 2015, Nat. Commun., 6, 7323 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y. W., & Dai, Z. G. 2007, A&A, 470, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yu, Y.-W., Zhang, B., & Gao, H. 2013, ApJ, 776, L40 [CrossRef] [Google Scholar]
- Yu, Y.-W., Liu, L.-D., & Dai, Z.-G. 2018, ApJ, 861, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y.-W., Chen, A., & Li, X.-D. 2019, ApJ, 877, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. B., Zhang, B., Sun, H., et al. 2018, Nat. Commun., 9, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z.-Y., Zhou, E.-P., & Li, A. 2018, ApJ, 862, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Yang, Y.-P., Liu, L.-D., et al. 2020, ApJ, 897, 20 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Adopted parameter values for the tentative fitting of the observations of GRB 160821B.
All Figures
 |
Fig. 1. Multi-wavelength light curves of the afterglow emission of GRB 160821B for different electromagnetic bands as labeled. The observational data are taken from (Lamb et al. 2019; Troja et al. 2019) and Swift. The dotted, dash-dotted, dashed, and solid lines correspond to the emission from the jet external shock, the thermal kilonova, the PWN, and their combination, respectively. The insert shows the early X-ray afterglow plateau, which may indicate the remnant NS could intrinsically be a magnetar before its surface magnetic field is buried. |
| In the text | |
 |
Fig. 2. Ultraviolet–optical–infrared spectra of the afterglow emission of GRB 160821B for different times as labeled. The observational data are taken from (Lamb et al. 2019; Troja et al. 2019). The dotted, dash-dotted, dashed, and solid lines correspond to the emissions of the jet external shock, the thermal kilonova, the PWN, and their combination, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



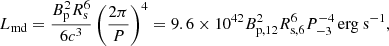
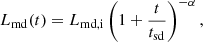
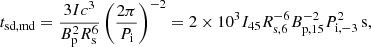
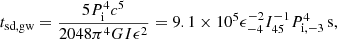
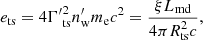
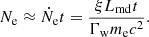
![$$ \begin{aligned} N_{\rm e,rel}=N_{\rm e}\times \min \left[1,{t_{\rm col}\over t}\right], \end{aligned} $$](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq10.gif)
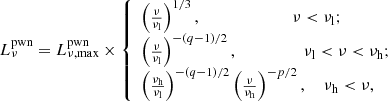
![$$ \begin{aligned} \rho _{\mathrm{ej} } (R , t) =\frac{ (\delta -3) M_{\mathrm{ej} }}{4 \pi R_{\max }^{3}}\left[\left(\frac{R_{\min }}{R_{\max }}\right)^{3-\delta }-1\right]^{-1}\left(\frac{R}{R_{\max }}\right)^{-\delta }, \end{aligned} $$](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq17.gif)
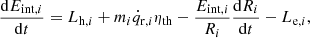
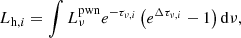
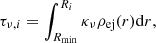
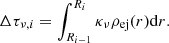
![$$ \begin{aligned} \dot{q}_{\mathrm{r} }=4 \times 10^{18}\left[\frac{1}{2}-\frac{1}{\pi } \arctan \left(\frac{t-t_{0}}{\sigma }\right)\right]^{1.3} \, \mathrm{erg}\, \mathrm{s} ^{-1} \,\mathrm{g} ^{-1} , \end{aligned} $$](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq25.gif)
![$$ \begin{aligned} \eta _{\mathrm{th} }=0.36\left[\exp \left(-0.56 t_{\mathrm{day} }\right)+\frac{\ln \left(1+0.34 t_{\mathrm{day} }^{0.74}\right)}{0.34 t_{\mathrm{day} }^{0.74}}\right], \end{aligned} $$](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq26.gif)
![$$ \begin{aligned} L_{\mathrm{e},i} =\frac{E_i}{\max \left[ R_i/c,t_{\mathrm{d,}i} \right]} , \end{aligned} $$](/articles/aa/full_html/2021/10/aa41325-21/aa41325-21-eq27.gif)