| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | C2 | |
| Number of page(s) | 1 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202039574e | |
| Published online | 24 August 2022 | |
HOLISMOKES
IV. Efficient mass modeling of strong lenses through deep learning (Corrigendum)
1
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild Str. 1, 85748 Garching, Germany
e-mail: schuldt@mpa-garching.mpg.de
2
Physik Department, Technische Universität München, James-Franck Str. 1, 85748 Garching, Germany
3
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of ASMAB, No.1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
4
Informatik Department, Technische Universität München, Bolzmannstr. 3, 85741 Garching, Germany
5
Pyörrekuja 5 A, FI-04300 Tuusula, Finland
Key words: gravitational lensing: strong / methods: data analysis / errata, addenda
In this erratum, we would like to correct a typographical mistake in Eq. (5) from Schuldt et al. (2021) that converts the complex ellipticity of an ellipse into its axis ratio q and position angle θ. Eq. (4) from Schuldt et al. (2021) gives the definition of the complex ellipticity as
which was used throughout the published article. For completeness, we gave a back transformation of the complex ellipticity into the axis ratio q and the position angle θ in Eq. (5). The expression for the axis ratio q ∈ (0, 1] is correct,
The error concerns the second part, the position angle θ ∈ [0, π), defined counter-clockwise with respect to the positive x-axis. According to Eq. (1) of this erratum, the cosine function corresponds to e x and the sine function corresponds to e y, which was unfortunately switched for the back transformation. A clearer and correct transformation is given by
with
and
Since we only used Eq. (1) (i.e., Eq. (4) from Schuldt et al. 2021) to transform the axis ratio q and position angle θ of our mock lenses into the complex parameterization for training the networks, and as we worked from then on in complex notation, we never used the back transformation. Therefore, this mistake does not affect any results in Schuldt et al. (2021).
References
- Schuldt, S., Suyu, S. H., Meinhardt, T., et al. 2021, A&A, 646, A126 [EDP Sciences] [Google Scholar]
© S. Schuldt et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



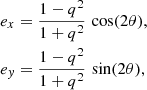
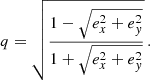
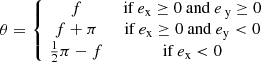
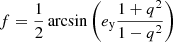
![$$ \begin{aligned} f \in [-\pi /4, +\pi /4]. \end{aligned} $$](/articles/aa/full_html/2022/08/aa39574e-20/aa39574e-20-eq5.gif)