EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 625 (May 2019) A&A, 625 (2019) A121 Full HTML
Free Access
Issue
A&A
Volume 625, May 2019
Article Number A121
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201935065
Published online 23 May 2019

© ESO 2019

1 Introduction

Planet–planet scattering (hereinafter P–P scattering) is a physical phenomenon that has been initially invoked to explain the high orbital eccentricities observed among extrasolar planets. According to the widely accepted core–accretion model for planet formation (Alibert et al. 2005), planets are expected to form on almost circular orbits. The subsequent onset of orbital instability may lead to a period of violent dynamical evolution dominated by close encounters between the planets. This phase ends only when one or more planets are ejected from the system on hyperbolic trajectories; a collision(s) occurs between two planets or a planet(s) impacts the host star. The initial configuration of the planetary system is permanently and dramatically altered and the surviving planets are left on stable highly eccentric noninteracting orbits possibly inclined with respect to the initial orbital plane (Weidenschilling & Marzari 1996; Rasio & Ford 1996; Marzari & Weidenschilling 2002; Namouni 2007; Chatterjee et al. 2008; Jurić & Tremaine 2008; Raymond et al. 2008, 2009; Nagasawa et al. 2008; Marzari 2010; Nagasawa & Ida 2011; Beaugé & Nesvorný 2012).

The onset of the chaotic behavior can occur at various stages of evolution of a planetary system. In the early phases, when the gaseous disk is still present, convergent migration (Masset & Snellgrove 2001; Lee & Peale 2002) may lead to crossing orbits and extended chaotic evolution (Marzari et al. 2010; Lega et al. 2013). However, the subsequent interaction with the residual gas of the disk may partly damp the acquired high orbital eccentricities of the surviving planets. Dynamical instability may also be triggered by the gas dispersal or it may suddenly start even after billions of years (Chambers et al. 1996; Marzari & Weidenschilling 2002; Veras & Mustill 2013). In this last case the planets must lay within the orbital stability limit (Gladman 1993; Donnison 2006; Marzari 2014), which depends on the masses and initial orbital parameters of the planets. Planet–planet scattering can also take place when an external perturbation acts on the planetary system like a stellar flyby (Shara et al. 2016), unless this phenomenon occurs in the early phases of evolution of a stellar cluster when its perturbing effects are erased by the gaseous disk damping (Marzari & Picogna 2013).

In its classical formulation, the P–P scattering model predicts that the inner planet gains the energy of the escaping planet(s) moving into a closer orbit which, however, has a semimajor axis only slightly smaller than the initial one. However, subsequently the energy loss due to tidal interactions with the central star might circularize its trajectory near the periastron distance (Barnes 2008; Nagasawa et al. 2008) and contribute significantly to populate the class of warm/hot Jupiters, i.e., gas giant exoplanets with very short orbital periods. In this context, the term eccentricity migration has been coined to indicate a giant planet that is likely formed at several astronomical units by core accretion, injected on an eccentric orbit, and has migrated very close to the star via tidal interaction. The eccentricity pumping may occur either because of P–P scattering or even for different dynamical paths such as Kozai interactions with an external massive companion (Fabrycky & Tremaine 2007; Naoz et al. 2011). By comparing the distribution of the minimum separation of hot Jupiters with their planet–star Roche separation, Nelson et al. (2017) deduced that about 85% of presently known hot Jupiters are possibly the outcome of eccentric migration while the others may be ascribed to disk-driven migration (Goldreich & Tremaine 1980).

In a recent paper, Petrovich et al. (2014) argued that P–P scattering events occurring close to the star cannot excite high eccentricities or inclinations in giant planets since they mostly end up in mutual collisions. As a consequence, they cannot explain the observed eccentric and potentially misaligned hot/warm Jupiters orbiting, for example, within 0.1 au. On this basis, these authors ruled out the scenario in which P–P scattering occurs after the planets are driven into close orbits by tidal interaction with the disk. Alternatively, they suggested that planet instability takes place far from the central star and the planets subsequently migrate on eccentric and inclined orbits until they get close to the star by interacting with the circumstellar disk. The occurrence of P–P scattering in the presence of the gaseous disk and far from the star has been studied with hydrodynamical simulations by Marzari et al. (2010); Lega et al. (2013). These simulations, in addition to those performed by Marzari & Nelson (2009) for giant planets and by Kley & Nelson (2012) for smaller planets, show that any initial high eccentricity and inclination of planets embedded in a disk are rapidly damped on a timescale on the order of a few 103 yr, almost independently of the initial semimajor axis of the planet. This complicates the scenario described by Petrovich et al. (2014) in which they assume that migration must shrink the semimajor axis of excited planets by at least 1–2 orders of magnitude without damping the eccentricity or inclination in order to produce hot/warm Jupiters on eccentric and misaligned orbits. Jupiter-mass planets might have some of their orbital eccentricity preserved by their interaction with the disk through Lindblad and corotation resonances (Goldreich & Sari 2003; D’Angelo et al. 2006; Duffell & Chiang 2015). However, the maximum eccentricity achieved by these mechanisms is small, on average on the order of the disk aspect ratio H∕r and it is limited to a maximum of 0.1–0.15 (for the more massive planets) while, for higher initial values of eccentricity, damping is confirmed in all simulations. Even assuming that planets close to their star can be influenced by the disk eccentricity, it is difficult to explain the high values observed among exoplanets.

Motivated by the results of Petrovich et al. (2014) derived with a pure N-body code that does not include the tidal interaction of the planets with the star and the effects of general relativity (hereinafter GR), we adopted a more complete model, derived by that used by Nagasawa et al. (2008), to simulate P–P scattering events occurring close to the star. This model, which already includes the effects of dynamical tides, has been improved by implementing the contribution from general relativity (isotropic, parametrized post-Newtonian). This improvement may affect not only the evolution of a single close planet, but also the secular evolution of a pair of planets (Mustill et al. 2014) and mutual collisions with merging. We then focused on three-planet systems in which we consider different initial distances from the star of the inner planet ranging from 0.03 to 1 au. According to population synthesis models based on core accretion and illustrated in Emsenhuber & Mordasini (in prep.) the fraction of multiplanet systems that form with either two or three giant planets is approximately the same but the P–P scattering dynamics for three planets is more diverse. We have run a large number of simulations and compared the outcomes with observations to test the reliability of our model. We also explored the influence of general relativity and dynamical tides on the final configurations of the systems.

In Sect. 2 we describe the numerical model used to simulate the evolution of a large number of putative three–planet systems moving initially close to the star. In Sect. 3 the possible outcomes of the dynamical instability are described. In Sect. 4 we show that general relativity can significantly alter the secular evolution of a pair of planets close to the star. In Sect. 5 we show how a random initial population of three planets evolved through the chaotic phase can well match the observed distribution. Finally, in Sect. 6 we summarize and discuss our results.

2 Numerical model

We modeled P–P scattering events for planetary systems initially made of three equal mass giant planets with m = 1 MJ. Population synthesis models have shown that these systems may be a common outcome of the initial phases of evolution of a circumstellar disk (Emsenhuber & Mordasini, in prep.), at least as frequent as systems consisting of two giant planets. We randomly selected the initial orbital parameters of the inner planet while the semimajor axis of the second and third planet are computed close to the stability limit so that instability occurs on a timescale typically shorter than 105 yr. This choice does not significantly affect the final orbital distribution of the planets after the chaotic phase as shown in previous models of P–P scattering (Weidenschilling & Marzari 1996; Rasio & Ford 1996; Marzari & Weidenschilling 2002; Namouni 2007; Chatterjee et al. 2008; Jurić & Tremaine 2008; Raymond et al. 2008, 2009; Nagasawa et al. 2008; Marzari 2010; Nagasawa & Ida 2011; Beaugé & Nesvorný 2012) and it allowed us to reduce the computational burden. The orbital angles of all planets are generated randomly while the initial eccentricity and inclinations are kept small, as expected from planet formation models.

In the numerical algorithm we included the effects of tides on the planet, mutual collisions, and GR. Modeling the tidal interaction between a planet and the star is a complex problem and many aspects of this interaction are not fully understood. In general, we should consider both equilibrium and dynamical tides. For static tides, dissipative and frictional processes within the planet remove energy from its orbit while for dynamical tides this occurs through the excitation and damping of oscillations (see, e.g., Ivanov & Papaloizou 2004, 2007; Ogilvie 2013; Mathis 2015).

In our model we included tides related to the fundamental modes and inertial modes of a planet in a state of pseudo-synchronization as describedin Ivanov & Papaloizou (2007). The energy transfer associated with the fundamental modes is minimal and no angular momentum transfer occurs in the state of pseudo-synchronization. The energy transfer associated with the fundamental modes (hereinafter ΔEf) and inertial modes (hereinafter ΔEin) excited in the planet are given by Eqs. (A7) and (100) of Ivanov & Papaloizou (2007), respectively, where we assume the typical coefficient 3 × 10−3 even for a 1 RJ planet. In our simulations, we modeled the tidal effect as impulsive changes in energy given by ΔEf + ΔEin to the planetary orbits at every periastron passage.

We neglected the contribution from dynamical tides raised by the planet on the host star according to the indications of Fig. 1. In this figure we compare the values of the energy transfer ΔEf and ΔEin, in unit of 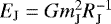EJ=GmJ2RJ−1$E_{\textrm{J}}=Gm_{\textrm{J}}^2R_{\textrm{J}}^{-1}$, with tides associated with spherical harmonic index ℓ = 2 and ℓ = 3 in the star whose polytropic index is n = 3 (hereinafter ΔEstar) as given by Lee & Ostriker (1986). In this case, G is the gravitational constant, MJ is the mass of Jupiter, and RJ its radius. To produce the curves in Fig. 1 we assume a planet with mass mp = 1 MJ and physical radius Rp = 1 RJ. The stellar mass is set to 1 solar mass (MS = 1 M⊙) and its radius is 1 solar radius (RS = 1 R⊙). Following these choices of the parameter values, 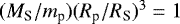(MS/mp)(Rp/RS)3=1$(M_{\textrm{S}}/m_{\textrm{p}})(R_{\textrm{p}}/R_{\textrm{S}})^3=1$. According to the predicted behavior of ΔEf, ΔEin, and ΔEstar, we can guess that inside of ~0.015 au planetary fundamental modes dominate the evolution of the system, while beyond ~0.015 au planetary inertial modes dominate the orbital evolution. The energy exchange due to the stellar tides (ΔEstar) is always lower than that of the planetary tides (ΔEf and ΔEin) in both regimes.

The trajectories of the planets are numerically integrated using a fourth-order time-symmetric Hermite code (Kokubo et al. 1998). Since at every periastron passage we need to update the energy due to the tidal interaction, we adopted a variable shared time step. A typical time step is on the order of 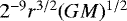2−9r3/2(GM)1/2$2^{-9}r^{3/2}(GM)^{1/2}$, where r is mutual distance and M is the total mass of the pair of interacting bodies.

In modeling P–P scattering events we considered three equal mass Jupiter planets (m = MJ) around a solar mass star. The force per unit mass acting on planet i is given by 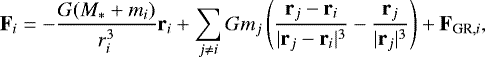Fi=−G(M*+mi)ri3ri+∑j≠iGmj(rj−ri|rj−ri|3−rj|rj|3)+FGR,i,\begin{equation*} \textbf{F}_i= -\frac{G(M_*+m_i)}{r_i^3}\textbf{r}_i +\sum_{j\neq i} Gm_{j}\left( \frac{\textbf{r}_{j}-\textbf{r}_i}{|\textbf{r}_{j}-\textbf{r}_i|^3} - \frac{\textbf{r}_{j}}{|\textbf{r}_{j}|^3}\right) +\textbf{F}_{\textrm{GR},i},\end{equation*}(1)

where the first term is the gravity from the star, the second term is the gravity from the other planets j, the third term is the indirect term due to the barycenter motion, and the forth term is the GR contribution computed in the post-Newtonian approximation with the correction terms given by Kidder (1995).

When two planets approach each other at a distance smaller than the sum of their radii, we assume that a collision occurs and merge the two bodies into a single body. The new velocity vector of this single body is computed from the conservation of momentum while its radius is derived adopting the same density of the other planets so that 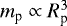mp∝Rp3$m_{\textrm{p}} \propto R_{\textrm{p}}^3$. We then continued the simulation with the new bigger planet. Owing to the largest radius of the merged body the tidal force becomes slightly stronger. Planets that hit the star are removed from the simulation while those that are fully circularized are no longer evolved in time.

thumbnail Fig. 1

Energy of tidal transfer during one periastron passage. A solar-mass and solar-radius star and a Jovian-mass and Jovian-radius planet are assumed. The energy transfer associated with the planetary fundamental mode ΔEf is given as a function of the periastron distance by a green broken line, the planetary inertial mode ΔEin by a blue line, and the energy associated with stellar tides ΔEstar by a black dotted line.

3 Planet–planet scattering outcomes

At the end of the chaotic evolution of three Jupiter size planets, we outline four main distinct possible outcomes:

  • 1.

    Ejection of one planet out of the planetary system, two planets are left on eccentric orbits, and the inner planet has a semimajor axis determined by conservation of orbital energy. This is the classical pure N-body P–P scattering event.

  • 2.

    Collision between two planets, both merger and scatterer are left on eccentric and inclined orbits or an additional collision occurs leaving a single eccentric planet in the system.

  • 3.

    Ejection of one planet and fast tidal circularization of the inner planet whose orbit shrinks enough to avoid further close encounters with its scatterer.

  • 4.

    Collision between two planets and tidal circularization to a close orbit of the inner planet, which may be either the more massive or the less massive of the two survivors.

Both events (3) and (4) may lead to hot Jupiters on orbits that can be significantly misaligned with respect to the star equator.

In Fig. 2 we show the typical output of a numerical simulation with three equal mass Jupiter planets. They are initially set on orbits with semimajor axis of 1, 1.5, and 2 au, respectively. All of these orbits are circular and with a random initial inclination lower than 1°, while all the other orbital angles are randomly chosen between [0,2π]. The initial orbits are close enough to lead to instability on a short timescale and are a reasonable outcome either of convergent migration or of in situ formation. The evolution of the system is followed for 2 Myr and, at the end, the different behaviors are grouped according to the previous classification. The classical scattering events bring the inner planet on an eccentric orbit around 0.2 au, according to the conservation of the orbital energy of the system. Two-planet collisions give rise to a second population of inner eccentric planets located close to 0.4 au. On average, these planets are less eccentric compared to those coming out of pure scattering events and their possible evolution is outlined and discussed in more detail in Fig. 6. In a significant number of cases the inner planet decouples from the outer planet and is circularized by tides to the pericenter of the scattered orbit, around 0.01–0.03 au. The inclination distribution shows that these last planets are often on highly misaligned orbits and one is even on a retrograde orbit.

These results are in agreement with the findings of Nagasawa et al. (2008) even if a larger number of collisional events are found owingto the initial closer orbit of the inner planet (Petrovich et al. 2014). However, in spite of the large number of collisions, events (3) and (4) supply a significant number of misaligned hot Jupiters while events (1) and (2) lead to eccentric and potentially misaligned planets on close orbits even when a collision occurs.

The final location of close-in giant planets in our models reflects the strength of the tides that we include in our modeling, which play a very important role in the decay of planetary orbits. These are dynamical tides (e.g., Lai 1997; Ivanov & Papaloizou 2004, 2007, 2011) and in our simulations we used a formulation given by Ivanov & Papaloizou (2007) as described inSect. 2. However, the impulse approximation used in the evaluation of dynamical tides becomes a poor approximation when the circularization proceeds (e.g., Mardling 1995a,b) and the eccentricity becomes low. Equilibrium tides become then effective (e.g., Beaugé & Nesvorný 2012 and references therein) and the tidal evolution may occur on a longer timescale. In short, at the beginning of the orbital evolution that leads to the formation of hot/warm Jupiters, dynamical tides are important in forcing the decay of the orbit. In the last part of the dynamical evolution when the eccentricity has become low, equilibrium tides are more important in determining the location where the planet stops. Unfortunately, at present it is not known when and how the two tides switch. When we change the magnitude of two tides, the final location of the planets can be adjusted (Beaugé & Nesvorný 2012). However, rather than introducing artificial effects, we continue to use dynamical tides in our simulations even for low eccentricities but we stop our simulations when the energy, decreasing from the tide at the pericenter, overcomes the orbital energy leading to a clustering of tidally circularized planets around 0.02 au. However, the final distribution of the inclination of the planets does not depend on this choice and highly misaligned planets would be produced anyway. Since the tidal evolution of planets with arbitrary inclinations is still not well known, we assume that planetary inclination is not significantly changed during tidal evolution (Barker & Ogilvie 2009). Thus, the planets maintain the inclination they have when the circularization begins.

If the orbits of the planets are initially set closer to the star, a larger number of collisions occurs at the expense of the pure scatteringevents where a planet is ejected from the system. In Table 1 we report the statistical distribution of the different outcomes of P–P scattering for increasingly smaller initial semimajor axis of the inner planet a1. Below 0.5 au the number of pure scattering events drops quickly to zero and there is a consistent reduction of tidal circularized planets in these kinds of events. On the other hand, there is an increase of events in which after a collision the merged planet, or its lighter companion, is progressively circularized by tides.

In Sect. 5 we discuss the orbital distribution of the planets for different initial values of a1.

thumbnail Fig. 2

Eccentricity vs. semimajor axis (top plot) and inclination vs. semimajor axis (bottom plot) of P–P scattering outcomes for three Jupiter-size planets started on circular orbits with a1 = 1 au, a2 = 1.5 au, and a3 = 2 au. All other initial orbital elements are selected randomly, the orbital angles between [0,2π] and the inclination smaller than 1°. The time evolution of each system is 2 My.
Table 1

Statistics of P–P scattering events as a function of the distance from the star.

4 Effectsof general relativity on the secular evolution of two planets

The main effect of GR is to induce the precession of the periapsis of a planet orbit according to the following equation (in the PN approximation): 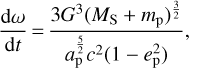dωdt = 3G3(MS+mp)32ap52c2(1−ep2),\begin{equation*} \frac {\textrm{d} \omega} {\textrm{d}t }\,{=}\,\frac {3 G^3 (M_{\textrm{S}} + m_{\textrm{p}})^{\frac {3}{2}} }{ a_{\textrm{p}}^{\frac{5}{2}} c^2 (1-e_{\textrm{p}}^2)},\end{equation*}(2)

(Misner et al. 2017). The precession rate is faster for planets close to the star and on eccentric orbits because of the 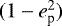(1−ep2)$(1-e_{\textrm{p}}^2)$ term at the denominator. This implies that if the outcome of a P–P scattering event injects a planet in an inside and eccentric orbit, Kozai–Lidovoscillations of eccentricity from an external perturbing planet are gradually quenched (Naoz 2016). It is then expected that the number of tidal circularization is somewhat reduced, but not significantly since the timescale of the Kozai cycle induced by an outer planetary companion may be fast (Nagasawa & Ida 2011), in particular in the close configurations we are considering in this paper. As a consequence, we do not expect significant changes due to the interaction between the Kozai–Lidov effect and relativity.

On the other hand, if the architecture of the planetary system does not involve significantly misaligned planets that can lead to a Kozai–Lidov evolution, GR is relevant since it can significantly affect the classical secular oscillations of eccentricity and perihelion longitude. In Fig. 3 we illustrate the evolution of a planet close to the star with semimajor axis a1 = 0.1 au perturbed by an outer planet with a2 = 1.5 au. The mutual inclination is 3° and the initial eccentricity is set to 0.15 and 0.3 for the inner planet and 0.1 for the outer one. We neglect in these models the contributionfrom tidal forces. While the average forced eccentricity remains the same in the case with and without GR, the proper oscillations are significantly shrunk when the GR effects are accounted for. This can be understood, as a first approximation, in the framework of the second order secular theory of Laplace–Lagrange (Murray & Dermott 1999). The equation for the non-singular variables hi = eisin(ϖi) after the inclusion of the GR term becomes 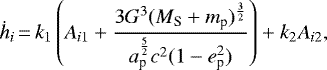h˙i = k1(Ai1+3G3(MS+mp)32ap52c2(1−ep2))+k2Ai2,\begin{equation*} \dot h_i\,{=}\,k_1 \left ( A_{i1} + \frac {3 G^3 (M_{\textrm{S}} + m_{\textrm{p}})^{\frac {3}{2}} }{ a_{\textrm{p}}^{\frac{5}{2}} c^2 (1-e_{\textrm{p}}^2)} \right ) + k_2 A_{i2} , \end{equation*}(3)

where ki = eicos(ϖi), while the matrices Ai,j are given in Murray & Dermott (1999) and are only functions of the semimajor axes and masses of the two planets. While for the first planet, and then for h1, the additional term is relevant, for the second planet (h2), the GR term can be safely neglected since the body is too far from the star for GR to be significant. The increase in the first diagonal term of the matrix Aii leads, in addition to a larger difference between the two main frequencies of the system and then to a faster oscillation frequency of the eccentricity, to an increase in the modulus of the term e11 of the first eigenvector associated with the secular evolution of the system. When we compare the evolution of two planets with and without GR but starting with the same initial conditions, we expect that an increase in |e11 | leads to a consequent decrease of |e12|, the first element of the second eigenvector. However, to comply with the fixed initial conditions, the term 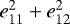e112+e122$e_{11}^2 + e_{12}^2$ must remain constant (both models start with ϖ1 − ϖ2 = π∕2) and, as a consequence, an increase in |e11| leads to a decrease in |e11e12|, which is the half-width of the secular oscillation. This is confirmed by the behavior shown in Fig. 3, where the amplitude of the secular oscillations of the case with GR is reduced compared to those without GR and the frequency is higher.

If we further increase the eccentricity of the inner planet, as in Fig. 4, the situation becomes more complex since the second order secular theory does not properly work at high eccentricities and higher order expansions of the perturbative potential are required as suggested in Libert & Henrard (2005). In this context, the interpretation of the numerical results on the basis of an analytical theory is more challenging and we prefer to show the outcome of the numerical integrations and guess a general trend. We again focus on two different models with different initial eccentricity and we also change the initial semimajor axis of the inner planet to show that the effects of GR on the secular evolution are relevant even farther from the star if the eccentricity is high. In Fig. 4 we show the case of a pair of planets where the inner planet has a semimajor axis of 0.2 au and an initial eccentricity of 0.6 and 0.8 in the two different cases, while the outer planet has a2 = 1.5 au and e2 = 0.1. As in the low eccentricity cases illustrated in Fig. 3, the proper oscillation is reduced in amplitude but in contrast to the low eccentricity cases, the forced term is larger. As a result, the peak eccentricity is approximately equal in the two cases (with and without GR) but the mean eccentricity in the model with GR is higher because of the smaller oscillation amplitude. This has significant implications for the interpretation of a statistical sample of giant exoplanets and for the high-eccentricity migration mechanism (Petrovich & Tremaine 2016). If we analyze a set of exoplanetary systems with two planets where one is close to the star, a prediction of their expected mean eccentricity based on a secular model without GR would underestimate its mean value. By inspecting Fig. 4 it can be inferred that GR, by increasing the lowest value of the secular oscillation, gives a higher mean eccentricity.

The growth in the average eccentricity of the inner planet significantly influences its tidal evolution as well. In Fig. 5 we illustrate the evolution of a system where the semimajor axis of the inner planet is a1 = 0.1 au and the initial eccentricity is set to 0.8, which is the same value of the high eccentricity case in Fig. 4. In this model we also include the tidal force on the planets to test the combined effects of tides and GR. The evolution of the eccentricity when the GR effects are included shows high frequency tiny oscillations around an almost linearly decreasing trend due to tidal damping. These fast oscillations indicate that the evolution of ϖ1 is dominated by the GR term, which also forces the eccentricity to remain constantly high. Without the GR term, the secular evolution shows wide oscillations also damped by the tidal interaction but on average the planet eccentricity is lower with respectto the GR case. This different behavior of the eccentricity also affects the semimajor axis evolution. With GR, the eccentricity is slowly damped but the permanence of the planet in a highly eccentric orbit favors a faster andsmoother inward migration of the inner planet (bottom panel of Fig. 5) compared to the case without GR. The so-called secular high-eccentricity migration (Petrovich & Tremaine 2016) is then enhanced and GR leads to a faster inward drift of the inner planet compared to the secularly oscillating case without relativity. This behavior favors the evolution of eccentric giant planets into hot/warm Jupiters on circularized orbits.

thumbnail Fig. 3

Secular evolution of the eccentricity of the inner planet of a pair whose orbits have been integrated with and without the GR term. The semimajor axis of the inner planet is a1 = 0.1 au while its eccentricity is set to e1 = 0.15 and e1 = 0.3 in the two different cases. The outer planet has a2 = 1.5 au and its eccentricity is e2 = 0.1. The mutual inclination is initially set to 3°. Tidal forces are not included in these models.
thumbnail Fig. 4

Same as in Fig. 3 but the semimajor axis of the inner planet has been shifted outward to a1 = 0.2 au to show that GR is relevant even further out. The initial eccentricities of the planets are e1 = 0.6 and e1 = 0.8 while that of the outer planet is fixed to e2 = 0.1.
thumbnail Fig. 5

As in Fig. 4 but the semimajor axis of the inner planet is set initially to 0.1 au and tidal forces are included. In the top panel the eccentricity of the inner planet is plotted with and without GR and both show the effects of tidal damping.

5 Planet–planet scattering close to the star

To gain a better insight on the outcomes of P–P scattering events occurring close to the star and on how they compare to the observed orbital distributions of the known exoplanets, we performed three different sets of simulations in which the initial semimajor axes of the inner planet a1 are randomly selected between 0.03–0.05 au, 0.05–0.1 au, and 0.2–1.0 au, respectively. The other two planets are started on orbits separated by 3RH, where RH is the Hill’s sphere. The results are shown in Fig. 7 for all cases and they are compared to the observed distributions of exoplanets more massive than 0.5 MJ (Schneider et al. 2011)1 added in the bottom panels. In the semimajor axis versus eccentricity distribution of observed exoplanets (bottom left panel of Fig. 7) there are two noticeable overdensities, one close to 0.05 au and the second just beyond 1 au. These peaks may tell us something about the dynamical evolution of giant planets or they may simply be due to an observational bias since most of the very close planets are detected by transits while the outer planets have been mostly revealed by radial velocities. The pileup in the proximity of 1 au suggested by some authors as due to inhomogeneities in the protoplanetary disks related to dead zones, ice lines, heat transitions (Hasegawa & Pudritz 2012), or photoevaporation (Matsuyama et al. 2003; Alexander & Armitage 2009; Alexander & Pascucci 2012; Ercolano & Rosotti 2015) has been recently re-evaluated and questioned by Wise & Dodson-Robinson (2018a,b). Additional detections are needed to have the final say on the (a,e) distribution of giant planets close to their star and on the origin of it. Very few data are presently available on the planet orbital misalignment with respect to the rotation axis of the star; this can be seen in the bottom right panel of Fig. 7, where all the available data obtained thanks to the Rossiter-McLaughlin effect are reported.

If we combine the outcome of our modeling, where a1 = 0.03–0.05 au (top left panel) and a1 = 0.05–0.1 au (second left panel), the surviving inner planets well reproduce the first observed peak in the semimajor axis versus eccentricity distribution (lowest left panel). High eccentricities are not achieved in the numerical models for semimajor axes smaller than 0.1 au and this is partly due to the merging of two planets after a collision and to tidal effects. In these models the inner planet may be either the more massive, an outcome of a single or even double merging event, or the lighter planet that is not involved in a collision. According to observations, close exoplanets cover a wide range in mass and the majority are encompassed within four masses of Jupiter and this is compatible with the prediction that these close planets are the outcome of a collision between two Jupiter size planets. The smaller planets might be the result of an impact between less massive planets possibly driven in close orbits by either type I migration or trapped and transported by disk inhomogeneities or formed in situ.

To interpret the outcome of the simulations shown in the two upper panels of Fig. 7, it is important to investigate the dynamical evolution of the planets after a collision between two. The planetary system, after a collision and merging, may follow different evolutionary paths (see Fig. 6). The two surviving planets can end up in a stable secular configuration where they evolve in time according to the standard linear secular theory (blue line in Fig. 6). Alternatively, after the collision, the surviving planets are still in a chaotic state where the orbits cross each other. During this instability the eccentricity of both planets is further excited until either they collide, leaving a single massive planets in the system on an eccentric orbit (red line in Fig. 6), or the inner planet is affected by tides and its orbit decouples from that of the outer planet (green and black line of Fig. 6). In this last case, the inner planetcan be either the more massive or the lighter planet. After the dynamical decoupling, the system follows two different paths depending on the distance of the planet from the star. If the planet is in a very close orbit it maybe affected by tides, as in the case illustrated by the black line in Fig. 6, and can be circularized to the pericenter; or the planet may remain on a highly eccentric orbit if it is not close enough to the star to be significantly affected by tides. In most of these configurations, the final outcome is a system with two planets close to the star and on eccentric orbits. Among the different final architectures of the planets after the chaotic phase and a collision, there are cases in which the inner planet is circularized by tides while the outer is close to the inner planet but dynamically decoupled from it. This last planet is a good candidate to be detected by transit time variations (TTV) on the orbit of the inner planet due to the strong mutual secular perturbations.

An aspect that is not well reproduced by the models where the scattering/collision occurs close to the star (two upper panels of Fig. 7) is the inclination distribution. All simulations with the inner planet starting within 0.1 au; the spin/orbit misalignment is typically lower than 20°. These low inclinations do not fully comply with observations since exoplanets found on close orbits may also be significantly misaligned with respect to the spin axis of the star (lowest right panel of Fig. 7). For example, the hot Saturn KELT-6b (Damasso et al. 2015) is on a misaligned orbit with the projected spin-orbit angle λ, measured thanks to the Rossiter-McLaughlin effect, of about 36°. As a consequence, the inner peak in the orbital distribution of observed exoplanets can be well reproduced by P–P scattering events with the exception of misaligned hot/warm Jupiters.

This apparent conflict between models and observations can be solved in two ways. One possibility is that the planets are driven into close orbits on already inclined orbits, but we have already argued that this cannot happen in presence of the gaseous disk which quickly damps the inclination. Alternatively, our simulations show that the problem can be solved when we consider P–P scattering events taking place farther out from the star. In the third row of Fig. 7 we draw the orbital distribution of surviving planets from a population where the inner planet had its semimajor axis randomly distributed in between 0.2 and 1.0 au. The semimajor axis versus eccentricity distribution shows a density peak of eccentric planets around 1 au with eccentricity values higher than 0.9 coming mostly from scattering events. This peak may conceivably be correlated with the observed peak, even if it is related to the particular choice of starting conditions. We may easily deduce that if we slightly increase the value of a1, we can move the peak outward. We can thereby obtain an even better match to the 1 au pileup, although it may be a bias artifact. The important aspect of the P–P scattering events occurring within a1 = 0.2–1.0 au is that they supply a significant number of circularized planets on misaligned orbits. In the right panel of the third row in Fig. 7 we note a significant number of these planets that fill the region left empty by the previous models where the inner planet was initially closer to the star. The misaligned Jupiters are, in the majority of cases, the output of scattering events without collisions and, in a limited number of cases, even retrograde orbits are obtained.

When comparing modeling outcomes with the real distributions of exoplanets we have to take into account that the simulations show the final distribution after the same fixed time span of the numerical integration while the observed semimajor axis, eccentricity, and inclination distributions group together systems with different evolutionary ages. This is a common problem in this type of modeling and it may lead to an overestimate or underestimate of the number of circularized systems. In the observed systems some planets had enough time to be further circularized compared to the simulations. However, in our numerical model dynamical tides tend to cause a fast evolution when the eccentricity is low and static tides should play a major role. As a consequence, the two effects might somehow balance and make our results more robust.

thumbnail Fig. 6

Eccentricity evolution of the planet ending up in the inner orbit after a collisional event involving two of the three initial planets. Different starting values of the planet semimajor axes are adopted. The legend within the figure gives the final semimajor axis of the inner planet when a dynamically stable configuration is reached. Different dynamical final states are illustrated. The blue line shows a regular secular evolution of the two surviving planets after the collision. The black line shows a sharp grow of the eccentricity during the chaotic evolution followed by a slow tidal damping of the inner planet, the less massive of the two. The red line shows a case where two collisions occur and a single massive planet is left on aneccentric orbit. The green line shows the case in which the merged planet ends up into a highly eccentric orbit and its evolution is decoupled from the outer planet.
thumbnail Fig. 7

Comparison among model orbital distributions for multiple initial values of the inner planet semimajor axis a1 and the distribution of presently known exoplanets (Schneider et al. 2011). Top panels: a1 is randomly selected within the interval 0.03–0.05 au, second row panels: within 0.05–0.1 au, third row panels: within [0.2-1] au. Bottom panels: observed orbital distribution. The inclination with respect to the star equator (λ parameter) is known only in a limited number of cases.
thumbnail Fig. 8

Radii of all exoplanets known to date (RJ is Jupiter’s radius) with mass in between 0.8 and 1.2 MJ (MJ is Jupiter’s mass) as a function of the pericenter distance q.

6 Dependence on the radius of the planet

So far, in our simulations we have assumed for all planets a radius comparable to that of Jupiter. However, the mass–radius relation may change depending on the orbital distance, stellar luminosity, age, and composition of the planet. In particular, young planets are expected to undergo subsequent cooling and contraction so that their initial radius is inflated compared to that of mature planets. According to the models of Fortney et al. (2007) and Mordasini et al. (2012), where current equations of state and heavy element enrichment have been adopted, young inflated Jupiter-like planets may reach radii as large as 1.5–1.6 RJ where RJ is Jupiter’s radius. Besides model predictions, we can also look at the presently observed population of transiting exoplanets with known mass and radius. In Fig. 8 we plot the radius rp of all observed exoplanets to date in the mass range 0.8Mj < mp < 1.2MJ (Schneider et al. 2011)2 as a function of their pericenter distance from the star. Most data concerns planets close to their host star since the radius is derived from transits and only a few values are known far from the star. If we limit the sample to only those planets with pericenter within 0.1 au and exclude the pulsar planet PSR 1719-14 b, the average value of rp is 1.33 RJ while the median is slightly smaller and equal to 1.28 RJ; the two extremes are Kepler-435, which has the largest radius (2.10 RJ) and WASP-129 b, which has the smallest radius (0.93 RJ). In this sample of real planets it is however difficult to disentangle the different effects that contribute to the radius distribution because of the concomitant presence of planets with different ages and different heavy element content and core size. In Fig. 8 we expect to look at planets that are inflated either because of stellar irradiation or because they are young and not yet cooled to their final temperature. In addition, the different composition influences both these effects introducing an additional spread in the density values for a given planet mass. While the age may be estimated from that of the star, the composition at present is almost impossible to be determined.

Since inour dynamical simulations both the collision probability and the tidal dissipation depend on the radius of the planets, we performed an additional set of simulations with a larger radius for the planets (i.e., lower density). Instead of using an average value derived from observations (1.33 RJ), we prefer to deal with a more extreme case and for all three planets we adopt a radius of 1.5 RJ. This choice allows us to better explore the effect of an inflated radius on the P–P scattering dynamics and it also covers the majority of observed planets which, according to Fig. 8, mostly populate the region below this value. It could be argued that this value is indeed appropriate for young planets evolving close to the star. On the other hand, P–P scattering events do not necessarily occur when the planets are young since the onset of instability and chaotic behavior can occur even after some billions of years from the formation of the planets, depending on their mutual distance at the time of the disk dissipation (Weidenschilling & Marzari 1996; Chambers et al. 1996). In the future, when the mass–radius relationship is better defined as a function of the planet age and, possibly, composition, it might be possible to build up a numerical model for P–P scattering in which the radius changes with time. However, there is an intrinsic limit for this kind of modeling set by the integration time. If the planets are close to the star, a numerical simulation can cover time intervals on the order of only some million years with a reasonable CPU load. Beyond that, the time required to complete the runs becomes prohibitively long, preventing any chance of covering a significant range of evolution of the radius of the planets.

In Fig. 9 the outcomes of the simulations with rp = 1.5 RJ are shown and can be compared to the cases illustrated in Fig. 7. In the top two panels showing the P–P scattering events with the inner planet very close to the star (a1 = 0.03–0.05 au), it is noteworthy that the number of planets with circularized orbits is significantly increased. In the standard case with rp = 1.0 RJ the tidally circularized planets (after a collision) were 16% while this percentage grows to 46% in the case with rp = 1.5RJ. This is an indication of the increased strength of the tide for inflated planets. However, the overall final eccentricity distribution still shows eccentric bodies, in particular the companions of those scattered inward. As a consequence, even for expanded planets we expect to find a significant number of eccentric planets close to their star and possibly cohabiting with an outer close-by planet causing observable TTVs. The final inclination distribution does not show interesting differences in the two cases and only mild values of inclination are achieved.

When the initial semimajor axis of the inner planet is chosen in the range a1 = 0.05–0.1 au, no significant differences are observed in the occurrence of the different outcomes of the P–P scattering events compared to the case with rp = 1 RJ. There is instead a decrease in the number of highly eccentric planets with ep > 0.5 when a larger radius is adopted and this is an additional indication of a stronger tidal circularization during the P–P evolution. Even in this case the final inclination distribution does not differ in the two scenarios. In the third row of Fig. 9 where the semimajor axis of the inner planet is moved further outward (a1 = 0.2–1.0 au), the effects of the inflated radius is almost negligible and the outcomes of the simulations are consistent with the case with rp = 1 RJ. The fraction of scattering events without collisions is approximately 15% when rp = RJ and 13% for rp = 1.5 RJ. This limited reduction in the scattering probability suggests that in both models (at equilibrium or inflated planets) the scattering cases occur under similar conditions where a quick increase in inclination favors close encounters rather than collisions. We observe an increase in the number of tidally circularized planets after a collision when rp = 1.5 RJ, which is an additional indication of the enhanced tidal force for inflated planets. The farther out we get from the star, the less inflated the planets are expected to be so we focus only on cases within 1 au where we find a good agreement with the observed orbital distribution of exoplanets for inflated planets as well (Fig. 7, bottom panels).

thumbnail Fig. 9

Same as Fig. 7 but with the radius of the planets increased to 1.5 RJ.

7 Discussion and conclusions

We have explored in this paper the dynamical outcome of P–P scattering events occurring when the planets are driven (or born) close to their parent star. The goal is to check if these events can explain the high eccentricities of a significant fraction of close-in Jupiter-size planets and the large misalignment with respect to the planet equator measured for some of these planets. Our numerical exploration is performed with a model that includes GR terms in the PN approximation, dynamical tides, and handles potential collisions between pair of planets and with the star. General relativity and dynamical tides were not included in the models of Petrovich et al. (2014) and this may explain why eccentric and misaligned planets did not come out from their simulations. We actually find that these two physical aspects significantly contribute to determine the final outcome of a P–P scattering event even if in different ways. General relativity, by changing the pericenter circulation frequency of the inner body, alters the secular evolution of a pair of planets close to the star. In particular, our modeling shows that the secular free oscillations of the inner planet are damped while the forced eccentricity term is increased, leading to an higher average eccentricity. This effect has implicationson the inward tidal migration, which is determined by the orbital eccentricity modulating the pericenter distance. An important contribution of tides is that they may dynamically decouple the pair of planets surviving after a period of chaotic evolution marked by mutual close encounters. As a consequence, two planets can be found on stable eccentric orbits even if one of the planets is the outcome of a merging event. This decoupling is responsible for the formation of eccentric planets even when the planets begin their chaotic evolution very close to the star.

By comparing the outcomes of our numerical modeling with the observed distribution of Jupiter-size planets, we find a good match even if we do not have an explanation for the observed gap around 0.2 au unless some other dynamical mechanism prevents the planets to populate this region. However, this gap is suspected to be related to observational biases and for this reason we do not try to model it by introducing predetermined and ad hoc initial conditions. It is noteworthy that, according to our simulations, the majority of misaligned close-in giant planets should be the outcome of P–P scattering events where the inner planet is initially located beyond 0.2 au. If the inner planet is started on closer orbits, the surviving stable planets move near their star but on low inclination trajectories. Because of the scarcity of data on planet–star misalignment, we cannot predict the fraction of planets in close orbits that come from beyond 0.2 au. Additional observations are needed to derive a more robust estimate.

Considering that the giant planets we deal with are located very close to the star and may be inflated either by stellar irradiation or because they are young and in the early stages of their contraction, we tested the relevance of the planet radius rp on the dynamical evolution of chaotic three-planet systems. The planetary radius is an important parameter as it determines the impact cross section and the strength of the tidal interaction. As an extreme case, we adopt a radius of 1.5 RJ for all the planets in the model and the same simulations performed for rp = RJ are run a second time with 1.5 RJ for comparison. The chaotic evolution is only significantly influenced by the change in rp for a system in which the inner planet is very close to the star. An increase in the number of circularized planets is observed while the overall eccentricity distribution shows slightly lower values. These effects, due to the increased strength of the tidal interaction, become progressively less relevant when the inner planet is moved outward and are negligible when a1 is located beyond 0.2 au. The increase in the cross section of the planets seems to be more relevant in terms of enhancing the tidal effects rather than reducing the number of scattering events which, within 1 au, is already small.

A potential limitation of our modeling is the use of dynamical tides even when the eccentricity of the planet is low and static tides should come into play. However, this does not invalidate the results since our model catches very well the dynamical evolution when the eccentricity of the planets is high and the most interesting dynamics occurs. The evolution predicted by dynamical tides is possibly too fast when the eccentricity becomes lower but, at that stage of evolution, the orbital circularization would be simply due to tidal interaction and it would not be influenced by the presence of other planets or by dynamical scattering. This implies that planets that are circularized in our model on a short timescale would follow the same path under the slower static tides on longer time spans. This, for instance, might be the case of HATS-52b (Henning et al. 2018), a two Jupiter mass planet with an eccentricity of 0.24 and a semimajor axis of 0.025 au, or that of HAT-P-56b (Huang et al. 2015), a similar size planet with the same eccentricity but with a semimajor axis of 0.042 au.

In most cases our modeling predicts the presence of an additional planet on an outer orbit. However, the second planet may be difficult to be detected by transits either because it is far from the star or because of the mutual inclination with respect to the inner planet owing to the scattering process. However, in those cases in which the second planet is also left on a close orbit, it might be detected via TTVs because of its secular perturbations on the inner planet. In this scenario, the models interpreting the TTV signal must take into account that very close to the star the secular theory is significantly affected by GR, as shown in Figs. 4 and 5.

When we compare our models with three initial planets to observations, we neglect those potential systems that were born with only two giant planets. These may undergo P–P scattering as well and contribute to the final observed population. However, due to the high frequency with which collisions occur when the planets have gravitational encounters close to their star, we expect that these configurations preferentially lead to the formation of systems with a single giant planet moving on a close and low-eccentricity orbit. The bottom left panel of Fig. 7 suggests that these single planets should contribute to the observed population of low-eccentricity close-in Jupiters, while those on eccentric/circularized and/or misaligned should originate from initially three-planet systems.

Acknowledgements

We thank an anonymous referee for useful comments and suggestions that helped to improve the paper. One of us (M.N.) was supported in part by JSPS KAKENHI Grant Number 17K05642 and 18H05438.

References

  1. Alexander, R. D., & Armitage, P. J. 2009, ApJ, 704, 989 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alexander, R. D., & Pascucci, I. 2012, MNRAS, 422, L82 [NASA ADS] [CrossRef] [Google Scholar]
  3. Alibert, Y., Mordasini, C., Benz, W., & Winisdoerffer, C. 2005, A&A, 434, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  5. Barnes, R. 2008, Exoplanets, ed. J. W. Mason (Chichester: Springer Praxis Books), 177 [CrossRef] [Google Scholar]
  6. Beaugé, C., & Nesvorný, D. 2012, ApJ, 751, 119 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chambers, J. E., Wetherill, G. W., & Boss, A. P. 1996, Icarus, 119, 261 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  8. Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
  9. Damasso, M., Esposito, M., Nascimbeni, V., et al. 2015, A&A, 581, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. D’Angelo, G., Lubow, S. H., & Bate, M. R. 2006, ApJ, 652, 1698 [NASA ADS] [CrossRef] [Google Scholar]
  11. Donnison, J. R. 2006, MNRAS, 369, 1267 [NASA ADS] [CrossRef] [Google Scholar]
  12. Duffell, P. C., & Chiang, E. 2015, ApJ, 812, 94 [Google Scholar]
  13. Ercolano, B., & Rosotti, G. 2015, MNRAS, 450, 3008 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  15. Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
  16. Gladman, B. 1993, Icarus, 106, 247 [NASA ADS] [CrossRef] [Google Scholar]
  17. Goldreich, P., & Sari, R. 2003, ApJ, 585, 1024 [NASA ADS] [CrossRef] [Google Scholar]
  18. Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  19. Hasegawa, Y., & Pudritz, R. E. 2012, ApJ, 760, 117 [NASA ADS] [CrossRef] [Google Scholar]
  20. Henning, T., Mancini, L., Sarkis, P., et al. 2018, AJ, 155, 79 [NASA ADS] [CrossRef] [Google Scholar]
  21. Huang, C. X., Hartman, J. D., Bakos, G. Á., et al. 2015, AJ, 150, 85 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ivanov, P. B., & Papaloizou, J. C. B. 2004, MNRAS, 347, 437 [NASA ADS] [CrossRef] [Google Scholar]
  23. Ivanov, P. B., & Papaloizou, J. C. B. 2007, MNRAS, 376, 682 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ivanov, P. B., & Papaloizou, J. C. B. 2011, Celest. Mech. Dyn. Astron., 111, 51 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jurić, M., & Tremaine, S. 2008, ApJ, 686, 603 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kidder, L. E. 1995, Phys. Rev. D, 52, 821 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kokubo, E., Yoshinaga, K., & Makino, J. 1998, MNRAS, 297, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  29. Lai, D. 1997, ApJ, 490, 847 [NASA ADS] [CrossRef] [Google Scholar]
  30. Lee, H. M., & Ostriker, J. P. 1986, ApJ, 310, 176 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lega, E., Morbidelli, A., & Nesvorný, D. 2013, MNRAS, 431, 3494 [NASA ADS] [CrossRef] [Google Scholar]
  33. Libert, A.-S., & Henrard, J. 2005, Celest. Mech. Dyn. Astron., 93, 187 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mardling, R. A. 1995a, ApJ, 450, 722 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mardling, R. A. 1995b, ApJ, 450, 732 [NASA ADS] [CrossRef] [Google Scholar]
  36. Marzari, F. 2010, Formation and Evolution of Exoplanets, ed. R. Barnes (Weinheim: Wiley-VCH), 223 [CrossRef] [Google Scholar]
  37. Marzari, F. 2014, MNRAS, 442, 1110 [NASA ADS] [CrossRef] [Google Scholar]
  38. Marzari, F., & Nelson, A. F. 2009, ApJ, 705, 1575 [NASA ADS] [CrossRef] [Google Scholar]
  39. Marzari, F., & Picogna, G. 2013, A&A, 550, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Marzari, F., & Weidenschilling, S. J. 2002, Icarus, 156, 570 [NASA ADS] [CrossRef] [Google Scholar]
  41. Marzari, F., Baruteau, C., & Scholl, H. 2010, A&A, 514, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Masset, F., & Snellgrove, M. 2001, MNRAS, 320, L55 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mathis, S. 2015, A&A, 580, L3 [Google Scholar]
  44. Matsuyama, I., Johnstone, D., & Murray, N. 2003, ApJ, 585, L143 [NASA ADS] [CrossRef] [Google Scholar]
  45. Misner, C. W., Thorne, K. S., & Wheeler, J. A. 2017, Gravitation (Princetion: Princeton University Press), 2017 [Google Scholar]
  46. Mordasini, C., Alibert, Y., Georgy, C., et al. 2012, A&A, 547, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge University Press), 1999 [Google Scholar]
  48. Mustill, A. J., Veras, D., & Villaver, E. 2014, MNRAS, 437, 1404 [NASA ADS] [CrossRef] [Google Scholar]
  49. Nagasawa, M., & Ida, S. 2011, ApJ, 742, 72 [NASA ADS] [CrossRef] [Google Scholar]
  50. Nagasawa, M., Ida, S., & Bessho, T. 2008, ApJ, 678, 498 [NASA ADS] [CrossRef] [Google Scholar]
  51. Namouni, F. 2007, in Lect. Notes Phys., eds. D. Benest, C. Froeschle, & E. Lega (Berlin: Springer Verlag), 729, 233 [NASA ADS] [CrossRef] [Google Scholar]
  52. Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
  53. Naoz, S., Farr, W. M., Lithwick, Y., Rasio, F. A., & Teyssandier, J. 2011, Nature, 473, 187 [NASA ADS] [CrossRef] [Google Scholar]
  54. Nelson, B. E., Ford, E. B., & Rasio, F. A. 2017, AJ, 154, 106 [NASA ADS] [CrossRef] [Google Scholar]
  55. Ogilvie, G. I. 2013, MNRAS, 429, 613 [NASA ADS] [CrossRef] [Google Scholar]
  56. Petrovich, C., & Tremaine, S. 2016, ApJ, 829, 132 [NASA ADS] [CrossRef] [Google Scholar]
  57. Petrovich, C., Tremaine, S., & Rafikov, R. 2014, ApJ, 786, 101 [NASA ADS] [CrossRef] [Google Scholar]
  58. Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  59. Raymond, S. N., Barnes, R., Armitage, P. J., & Gorelick, N. 2008, ApJ, 687, L107 [NASA ADS] [CrossRef] [Google Scholar]
  60. Raymond, S. N., Armitage, P. J., & Gorelick, N. 2009, ApJ, 699, L88 [NASA ADS] [CrossRef] [Google Scholar]
  61. Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Shara, M. M., Hurley, J. R., & Mardling, R. A. 2016, ApJ, 816, 59 [NASA ADS] [CrossRef] [Google Scholar]
  63. Veras, D., & Mustill, A. J. 2013, MNRAS, 434, L11 [NASA ADS] [CrossRef] [Google Scholar]
  64. Weidenschilling, S. J., & Marzari, F. 1996, Nature, 384, 619 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  65. Wise, A. W., & Dodson-Robinson, S. 2018a, Res. Notes AAS, 2, 29 [CrossRef] [Google Scholar]
  66. Wise, A. W., & Dodson-Robinson, S. E. 2018b, ApJ, 855, 145 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Statistics of P–P scattering events as a function of the distance from the star.

In the text

All Figures

thumbnail Fig. 1

Energy of tidal transfer during one periastron passage. A solar-mass and solar-radius star and a Jovian-mass and Jovian-radius planet are assumed. The energy transfer associated with the planetary fundamental mode ΔEf is given as a function of the periastron distance by a green broken line, the planetary inertial mode ΔEin by a blue line, and the energy associated with stellar tides ΔEstar by a black dotted line.
In the text
thumbnail Fig. 2

Eccentricity vs. semimajor axis (top plot) and inclination vs. semimajor axis (bottom plot) of P–P scattering outcomes for three Jupiter-size planets started on circular orbits with a1 = 1 au, a2 = 1.5 au, and a3 = 2 au. All other initial orbital elements are selected randomly, the orbital angles between [0,2π] and the inclination smaller than 1°. The time evolution of each system is 2 My.
In the text
thumbnail Fig. 3

Secular evolution of the eccentricity of the inner planet of a pair whose orbits have been integrated with and without the GR term. The semimajor axis of the inner planet is a1 = 0.1 au while its eccentricity is set to e1 = 0.15 and e1 = 0.3 in the two different cases. The outer planet has a2 = 1.5 au and its eccentricity is e2 = 0.1. The mutual inclination is initially set to 3°. Tidal forces are not included in these models.
In the text
thumbnail Fig. 4

Same as in Fig. 3 but the semimajor axis of the inner planet has been shifted outward to a1 = 0.2 au to show that GR is relevant even further out. The initial eccentricities of the planets are e1 = 0.6 and e1 = 0.8 while that of the outer planet is fixed to e2 = 0.1.
In the text
thumbnail Fig. 5

As in Fig. 4 but the semimajor axis of the inner planet is set initially to 0.1 au and tidal forces are included. In the top panel the eccentricity of the inner planet is plotted with and without GR and both show the effects of tidal damping.
In the text
thumbnail Fig. 6

Eccentricity evolution of the planet ending up in the inner orbit after a collisional event involving two of the three initial planets. Different starting values of the planet semimajor axes are adopted. The legend within the figure gives the final semimajor axis of the inner planet when a dynamically stable configuration is reached. Different dynamical final states are illustrated. The blue line shows a regular secular evolution of the two surviving planets after the collision. The black line shows a sharp grow of the eccentricity during the chaotic evolution followed by a slow tidal damping of the inner planet, the less massive of the two. The red line shows a case where two collisions occur and a single massive planet is left on aneccentric orbit. The green line shows the case in which the merged planet ends up into a highly eccentric orbit and its evolution is decoupled from the outer planet.
In the text
thumbnail Fig. 7

Comparison among model orbital distributions for multiple initial values of the inner planet semimajor axis a1 and the distribution of presently known exoplanets (Schneider et al. 2011). Top panels: a1 is randomly selected within the interval 0.03–0.05 au, second row panels: within 0.05–0.1 au, third row panels: within [0.2-1] au. Bottom panels: observed orbital distribution. The inclination with respect to the star equator (λ parameter) is known only in a limited number of cases.
In the text
thumbnail Fig. 8

Radii of all exoplanets known to date (RJ is Jupiter’s radius) with mass in between 0.8 and 1.2 MJ (MJ is Jupiter’s mass) as a function of the pericenter distance q.
In the text
thumbnail Fig. 9

Same as Fig. 7 but with the radius of the planets increased to 1.5 RJ.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.