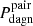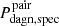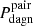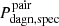| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833767 | |
| Published online | 16 April 2019 | |
Intrinsic and observed dual AGN fractions from major mergers
1
Departament de Física Quàntica i Astrofísica, Universitat de Barcelona, C. Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: jm.solanes@ub.edu
2
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona., C. Martí i Franquès 1, 08028 Barcelona, Spain
3
Departamento de Astronomía Extragaláctica, Instituto de Astrofísica de Andalucía, IAA–CSIC, Glorieta de la Astronomía s/n, 18008 Granada, Spain
4
Instituto de Astrofísica de Canarias, C. Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
5
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
Received:
4
July
2018
Accepted:
20
February
2019
A suite of 432 collisionless simulations of bound pairs of spiral galaxies with mass ratios 1:1 and 3:1, and global properties consistent with the ΛCDM paradigm, is used to test the conjecture that major mergers fuel the dual AGN (DAGN) of the local volume. Our analysis was based on the premise that the essential aspects of this scenario can be captured by replacing the physics of the central black holes with restrictions on their relative separation in phase space. We introduce several estimates of the DAGN fraction and infer predictions for the activity levels and resolution limits usually involved in surveys of these systems, assessing their dependence on the parameters controlling the length of both mergers and nuclear activity. Given a set of constraints, we find that the values adopted for some of the latter factors often condition the outcomes from individual experiments. Still, the results do not, in general, reveal very tight correlations, the clearest effect being the tendency of the frequencies normalized to the merger time to anticorrelate with the orbital circularity. In agreement with other theoretical studies, our simulations predict intrinsic DAGN abundances that range from ∼ a few to 15% depending on the maximum level of nuclear activity achieved, the higher the bolometric luminosity, the lower the fraction. At the same time, we show that these probabilities are reduced by about an order of magnitude when they are filtered with the typical constraints applied by observational studies of the DAGN fraction at low redshift. Seen as a whole, our results prove that consideration of the most common limitations involved in the detection of close active pairs at optical wavelengths is sufficient alone to reconcile the intrinsic frequencies envisaged in a hierarchical universe with the small fractions of double-peaked narrow-line systems which are often reported at kpc-scales.
Key words: galaxies: active / galaxies: interactions / galaxies: nuclei / methods: numerical
© ESO 2019
1. Introduction
Within the current paradigm of galaxy evolution through hierarchical structure formation the close pairs of active galactic nuclei (AGNs), which at kpc-scale separations are usually referred to as dual AGN (DAGN), are widely believed to be the later stages of major mergers of galaxies (e.g. Di Matteo et al. 2005; Hopkins et al. 2006; Colpi & Dotti 2011; Fu et al. 2011; Koss et al. 2012; Blecha et al. 2013; Ellison et al. 2013; Fan et al. 2016; Shangguan et al. 2016; Weigel et al. 2018), although some works seem to suggest otherwise (e.g. Cisternas et al. 2011; Schawinski et al. 2012; Hernández-Ibarra et al. 2016; Villforth et al. 2017). In binary mergers, as the progenitor galaxies orbit around each other, they transfer angular momentum to the dark matter (DM) and to each other through dynamical friction and start to sink toward the center of the system. If both members of the pair are gas-rich and massive enough to contain a central supermassive black hole (SMBH; Kormendy & Ho 2013), the gravitational torques generated on each close passage are expected to drive substantial inflows of gas to the inner regions of the merging objects, where it can be accreted into the central black hole (BH) and ignite nuclear activity. As the merger develops, the level of activity tends to progressively achieve higher values, with its peak likely at the galaxies’ final approach, when the two SMBH rapidly in-spiral to the center of the remnant and coalesce emitting the most powerful pulses of gravitational waves in the universe (Mingarelli et al. 2017). Of course, this idealized view does not prevent the nuclear activity from being (alternatively) restricted to one of the members of the pair, or triggered occasionally by interactions not necessarily leading to a merger, as observed in luminous quasars and radio sources (Ramos Almeida et al. 2011; Bessiere et al. 2012), or by secular (internal) processes (Moles et al. 1995; Márquez & Masegosa 2008). In any event, the detection and abundance of DAGN over galaxy-wide scales not only provides an essential test for the merger-driven scenario of these systems, but also has important implications for hierarchical structure formation theories, the growth and demographics of SMBH, the accretion and feedback physics, and even for our understanding of gravity.
Over the last decade a number of systematic studies of AGN pairs have been conducted at different wavelengths. Many have relied upon optical data, such as the searches for double-peaked narrow emission lines in the spectroscopic galaxy sample of the Sloan Digital Sky Survey (SDSS; e.g. Wang et al. 2009; Liu et al. 2010; Comerford et al. 2011; Ellison et al. 2011; Rosario et al. 2011; Ge et al. 2012). Yet there is no dearth of examples of studies based on observations at other wavelengths, such as those carried out in the X-ray (Koss et al. 2012; Teng et al. 2012), mid-IR (Satyapal et al. 2017), or radio windows (Fu et al. 2015; additional references can be found in Rubinur et al. 2018). In more than a few cases these investigations have reported a frequency of DAGN at kpc scales surprisingly low according to current observational constraints on the merger rate of galaxies, even after taking into account selection effects (e.g. Liu et al. 2011). Naive calculations that compare typical merging timescales to expected AGN lifetimes suggest that, in accordance with the plausible scenario described above, the fraction of DAGN in the local universe should be roughly one order of magnitude larger than the values ≲1% typically observed (e.g. Foreman et al. 2009). It must also not be forgotten that observational DAGN studies suffer from biases related to the wavelength and methodology used to diagnose the dual BH activity. They also suffer from incompleteness –in many cases severe– related to the design of the surveys, the identification of mergers, and the difficulty in resolving the pairs at small projected separations.
This work focuses precisely on the triggering and detectability of DAGN at kpc-scales in the nearby universe under the assumption that the dual nuclear activity takes place in bound pairs of similarly massive spiral galaxies (e.g. Steinborn et al. 2016). Our aim is to investigate the contribution of the limitations associated with the standard methodologies used for the detection of active SMBH pairs to the aforementioned conflict between theory and observations. We are particularly interested in assessing the importance in the selection of DAGN candidates of the constraints stemming from the observation of double-peaked narrow emission lines in optical spectra, as well as of the most common limitations related to the selection of close active companions around previously detected single AGN. In order to do so, we have used a large subset of simulated collisions between MW-like galaxies included in the massive suite of high-resolution isolated binary mergers recently analyzed by Solanes et al. (2018). While these merger experiments represent neatly and extensively the sort of gravitational encounters most likely involved in DAGN activation, they lack a self-consistent treatment of the complex physical processes that deliver the gas to the nuclear BH of the interacting galaxies. To solve this deficiency we have adopted the strategy of encoding the physics of the gaseous component by means of the kinematics of the collisions, representing it through a series of thresholds defined in the six-dimensional phase space of the relative separation of the two progenitor galaxies1. In addition, the intergalactic separations adopted as a proxy for the different levels of BH activity have been complemented by several sets of constraints, both along the line of sight (LOS) and in the plane of the sky, intended to represent the limitations habitually present in the photometric and spectroscopic, detection of AGN pairs.
The paper is laid out as follows. First, we outline in Sect. 2 the main characteristics and initial conditions of the major merger simulations used for the present study. Section 3 introduces the strategy devised to estimate from our experiments the incidence of DAGN in the local universe. We then discuss in Sect. 4 a number of possible alternatives for the calculation of this fraction and the different outcomes we obtain, paying special attention to the assessment of the importance of merger parameters. Finally, in Sect. 5, we analyze the validity of our estimates of the DAGN fraction from the standpoint of both observational studies and theoretical data provided by the latest state-of-the-art numerical simulations, while Sect. 6 summarizes our work and discusses the main insights that emerge from it. One long table and several large figures showing results for DAGN fractions in close pairs are included in Appendices A and B, respectively. All probabilities and magnitudes inferred in the present investigation have been calculated assuming a standard flat Λ Cold Dark Matter (ΛCDM) cosmology with H0 = 70 km s−1 Mpc−1, Ωm, 0 = 0.3 and ΩΛ, 0 = 0.7.
2. Numerical models of binary mergers
The runs used for the present investigation constitute the S+S subset of the suite of simulations of isolated binary galaxy mergers in bound orbits by Solanes et al. (2018; see this work for full details). The orbital configuration of the mergers is defined from the initial values of both the orbital energy and the orbital circularity. The former quantity is represented as usual by the dimensionless ratio
with Mp and Ms, respectively, being the virial masses of the primary and secondary progenitor galaxies, Rp the virial radius of the primary’s halo and rcirc(ℰ) the radius of a circular orbit with the same orbital energy ℰ. Likewise, the initial orbital circularity acts as a dimensionless proxy of the orbital spin
with ℒ = μrvtan, vtan the tangential component of the time derivative of the intercentric separation r = rp − rs and μ = MpMs/(Mp + Ms) the reduced mass of the system. The values chosen for these two quantities are representative of their probability density functions (PDF) predicted by the currently favored ΛCDM cosmological model. For rcirc, p two values are considered: 4/3, which approximates the peak of the heavily right-skewed orbital energy distribution found in the cosmological simulations by McCavana et al. (2012), and 2.0, intended to account for the relatively abundant more energetic orbits (we note that this second value of the orbital energy is applied only to equal-mass mergers without affecting the conclusions of this work). We also include collisions along three different orbital trajectories defined by ϵ = 0.20, 0.45, and 0.70. These values are arranged more or less equidistantly across the universal and heavily platykurtic PDF of the orbital circularity shown by galaxies in bound orbits (e.g. Benson 2005; Khochfar & Burkert 2006; Jiang et al. 2008), whose peak is at ϵ ∼ 0.5 (corresponding to an ellipticity e ≃ 0.9). Each initial orbital setup is combined with four different values of the dimensionless internal spin (Peebles 1969) of the progenitor galaxies that sample the main part of its similarly universal P(λ) where the probability is highest (e.g. Shaw et al. 2006; Hernandez et al. 2007; Bryan et al. 2013): λ = 0.00, 0.02, 0.04 (∼median), and 0.06, and which are assumed identical for both members of the pair. Finally, when defining the geometry of the encounters, we have also considered galaxies with different initial relative orientations. Since cosmological simulations suggest that the orientations of the spins of merging halos and of the orbital angular momentum are basically uncorrelated (Khochfar & Burkert 2006), we have put the focus on those extreme configurations (twelve) that maximize or minimize the coupling between the internal spin vectors of galaxies, or rotation axes, and the orbital spin, and hence that maximize or minimize the duration of the mergers (see Table 1).
Our model galaxies are made up of an extended spherical Navarro et al. (1997) DM halo whose global properties (mass, spin and concentration) are used to set the scalings of its central baryonic (stellar) core. The mass of the central luminous component of the galaxies is taken equal to 5% of their total mass and distributed in the form of an exponential disk of stars surrounding a non-rotating spherical Hernquist (1990) stellar bulge. We have adopted two values for the total mass ratio of the primary and secondary progenitors, η ≡ Mp/Ms = 1 and 3, which correspond to the boundaries of the major merger range. For the largest progenitors, intended to represent a ∼1012 M⊙ galaxy of Hubble’s Sb class, we have taken the bulge mass, Mb, to be equal to the 25% of the disk mass, Md, while the smallest progenitors, which picture local Sc galaxies, have Mb = 0.1Md (Graham 2001).
The largest galaxies are modeled using a total of 210, 000 particles, while for the smaller objects this number is scaled by the factor 1/η. All experiments adopt a 50–50 split in number between luminous and dark bodies. The Plummer equivalent softening length for the luminous particles is set to 30 pc, while for the more massive bodies (DM), the softening length was taken to be proportional to the square root of their body mass, thereby ensuring the same maximum interparticle gravitational force. Although the galaxy models allow a single extra particle representing a SMBH to be placed right at the center, the extent of the DAGN phenomenon has been simulated in practice by following the temporary evolution of the separation, in both the configuration (r) and velocity (v) spaces, between the central regions of the interacting galaxies (see Colpi 2014, and references therein), which in every snapshot are defined by the subsets of the 10% most bound stellar particles of each member of the pair. We also note that by following the center of mass of a collection of particles we avoid the relocation problems of the SMBH that arise sometimes in simulations. All the multi-component galaxy models used in the merger experiments settle into full dynamical equilibrium in a very short time (less than one rotation). Besides, we have verified that their structural and kinematic properties remain statistically unchanged for as long as a Hubble time when they are evolved in isolation.
The combination of the values of the parameters described above allows us to build a total of 288 Sb+Sb (η = 1) and 144 Sb+Sc (η = 3) distinct merger configurations. Their evolution was simulated using the serial N-body tree-code GyrfalcON (Dehnen 2000) with the adaptive time integration scheme enabled and a longest timestep of ∼0.001 simulation time units, equivalent to about 2 Myr. This figure should not be confused with the typical rate of the outputs of the simulation used in the analysis, which is about one snapshot per 30 Myr. Such rate, however, is increased to one snapshot per ∼10 Myr over the ±0.5 Gyr-period around the time of coalescence of the two nuclei to better capture the evolution of the separation of the central regions of the galaxies during the final stages of the merger. All the experiments begin with the galaxies separated by a distance equal to the sum of the virial radii of their respective dark halos and are kept running until well after (between ∼1–2 Gyr depending on the orbit) the formation of the merger remnant.
Regarding the merger timescale, τmer – a quantity involved in the calculation of some of the probabilities of detecting a DAGN outlined in Sect. 4.1 –, it is defined as the interval between the instant at which the center of mass of the satellite galaxy first crosses the virial radius of the host’s dark halo and the final coalescence of the baryonic nuclei of both galaxies into a single luminous core. Following Solanes et al. (2018), the separation in phase space is quantified by the secular evolution of the product of the (dimensionless) moduli, ΔrΔv, of the Euclidean intercentric distances of the merging galaxies in the configuration and velocity subspaces, respectively. Section 4 (in particular) of that paper, includes a detailed discussion of the role played by the different parameters that configure a merger, ranging from the initial orbital circularity and energy, to the mass ratio and morphologies of the progenitor galaxies, or to the magnitude and orientation of their initial internal spins, on the length of the merger.
Since gravity is the only physics in our simulations, we could in principle attempt to extend our predictions to different epochs (i.e. redshifts) simply by scaling masses, times and lengths. In practice, however, the fact that we take for both the halos’ concentration and the global properties of the stellar component values that are characteristic of the local universe rend this extrapolation unfeasible.
3. Setting the scene for the triggering and detectability of DAGN
The strategy adopted for the assessment of the incidence of DAGN in the local universe is based on the following assumptions:
-
DAGN are triggered in major (η ≤ 3) galaxy-galaxy mergers;
-
the activity of the nuclear BH is essentially encapsulated in the intercentric separation in phase space of the merging galaxies2; and
-
the level of activity increases with decreasing intergalactic separation.
Since we are interested in comparing our predictions with a variety of outcomes from observations and simulations, we have implemented up to three different maxima of intergalactic separation in the phase space when calculating the DAGN frequencies. In order to provide a sense of the prominence of the nuclear activity, we assumed that such separations are inversely correlated in a sensible way with certain thresholds of AGN bolometric luminosity, thus preserving the trend that more luminous duals tend to be closer to each other (Steinborn et al. 2016; Volonteri et al. 2016). The nuclear activity levels adopted are:
(i) WEAK, usually long-term (> 10 Myr), DAGN activity, which we assumed is related to low bolometric luminosity thresholds of around 1042 erg s−1, and that we associate with intrinsic phase-space separations Δr ≲ 50 kpc and Δv ≲ 200 km s−1, in reasonable agreement with the findings of controlled simulations (Van Wassenhove et al. 2012; Capelo et al. 2017) and observations (Koss et al. 2012);
(ii) INTERMEDIATE activity, which is expected to occur at Δr ≲ 10 kpc and that likely involves bolometric luminosities ≳1043 erg s−1; and
(iii) STRONG activity, triggered when Δr becomes smaller than about 2 kpc and where it is feasible to expect that the typical bolometric luminosity Lbol of the pair can reach values of at least 1044 erg s−1.
We stress again that the adopted identifications between phase-space boundaries and nuclear activity thresholds are only indicative and merely established to help the reader have a rough idea of the minimum bolometric luminosities that can be expected depending on the physical separation of the BH. Besides, as the luminosity of any AGN pair is expected to basically reflect the luminosity of its most massive member, we have not accounted for the possibility that the central BH can have different masses – something that can happen especially in unequal mass mergers – and therefore experience different feeding rates that may lead to different luminosities.
The total lifetime of the AGN phase triggered by the interactions (i.e., the duty-cycle of the central BH) is controlled by a parameter τagn which is allowed to range from 10 Myr up to a maximum of 100 Myr (Gatti et al. 2015; Capelo et al. 2017; Blecha et al. 2018). The calculation of probabilities assumes that there is no correlation between the span and strength of AGN activity – thus ignoring claims that AGN lifetimes may decrease with increasing luminosity (Blecha et al. 2018). For this reason, we have chosen to provide predictions for the two extreme values of this range, which will be hereinafter referred to as the SHORT and LONG BH duty-cycles, respectively. However, we have explicitly taken into account in our modeling that the nuclear regions of the galaxies take a while to perceive the effects of the interaction once their relative separation falls below the threshold adopted for the onset of a certain level of AGN activity. This happens because infalling matter must get rid of its angular momentum before it can begin to feed the central BH. This task, which is driven by kinematic viscosity and, most probably, magnetic fields, makes the accretion of matter into black holes a relatively slow process. A reasonable estimate, although admittedly crude, of the minimum time delay required for the start of any nuclear activity associated with a given intercentric distance in configuration space, Δr, is provided by the free-fall speed in a typical disk galaxy, which has been approximated by the expression
independently of the mass of the progenitors and the rest of merger characteristics. Furthermore, we have also assumed that once the nuclear activity of any level is triggered in a merger it will continue unaltered as long as the conditions for the feeding of the SMBH are met. In other words, that there is always enough material available to power the BH with an accretion rate below the Eddington limit (Kollmeier et al. 2006; Shen et al. 2008), so that the fuel supply is not substantially affected by feedback.
In an attempt to mimic the most frequent observational limitations that are encountered when trying to determine the abundance of DAGN, we have also implemented a procedure that aims to reproduce the incidence of dual systems with double-peaked narrow emission lines in their optical spectra (Zhou et al. 2004; Gerke et al. 2007; Comerford et al. 2009). Since, as mentioned above, there is a plethora of systematic surveys that apply this technique using as parent samples different data releases from the SDSS (e.g. Smith et al. 2010; Shen et al. 2011; Pilyugin et al. 2012; Müller-Sánchez et al. 2015, see also references in the Introduction above), we have modeled the limitations imposed by optical spectroscopic by restricting the detections to LOS velocity differences, Δv1D, larger than ∼150 km s−1 and projected separations, Δr2D, smaller than 8 kpc. The first constraint is set by the resolution of SDSS spectra, while the second corresponds to the projected distance inferred from an angle of 3 arcsec, the diameter of a single fiber, at a redshift of 0.15 typical of the SDSS Legacy Survey.
Another common approach to build up observational samples of DAGN – which is not limited by spectral resolution or fiber size – is to identify them from a (ideally complete) parent dataset of bona fide merger candidates containing individual spectral information (e.g. Ellison et al. 2011; Koss et al. 2012; Teng et al. 2012; Fu et al. 2015; Satyapal et al. 2017). This technique can be considered complementary of the former because it is sensitive to galaxy pairs with nuclear separations larger than those of the double-peak approach. To replicate what is usually done in practice, we have applied to our binary mergers up to three different filters – in projected intercentric distances and LOS velocities – representative of the most typical observational constraints adopted to define galaxy pairs in surveys at low redshift. They are:
(i) The OPEN filter, which applies the constraints adopted in Liu et al. (2011), who selected pairs with 5 kpc ≤ Δr2D ≤ 100 kpc and Δv1D < 600 km s−1, and where the lower limit on Δr2D is introduced to exclude pairs in advanced mergers with nuclear separations that are too small to be resolved by the deblending algorithm of SDSS photometry (Lupton et al. 2001);
(ii) The WIDE filter, which applies to pairs satisfying somewhat stricter criteria: Δr2D ≤ 80 kpc and Δv1D < 500 km s−1; and
(iii) The CLOSE filter, which is introduced to account for galaxy pairs selected with the conditions3 Δr2D ≤ 30 kpc and Δv1D < 500 km s−1 (e.g. Darg et al. 2010; Patton & Atfield 2008).
For the last two types of predictions we have assumed that there are no special difficulties when it comes to spatially resolve duals during the final phase of the mergers, so we have not imposed any minimum threshold in Δr2D. In any event, none of the results discussed in the following sections are significantly affected by the specific values adopted for the phase-space constraints.
As we have just seen, the observational identification of AGN pairs relies on projected quantities. Therefore, to derive the likelihoods for dual-activity observability that result from any of our merger simulations we must integrate the projections of the intrinsic intercentric distance and velocity vectors along all possible viewing angles. In practice, this means that it was necessary for us to deal with the cumulative distribution functions
for projections onto the 1D subspace defined by a given random LOS (it applies to radial velocities), and
for projections onto the 2D subspace defined by the plane perpendicular to the LOS (it applies to distances in the plane of the sky), with 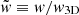 the magnitude w of the projection of an arbitrary 3D vector in units of the modulus w3D of the latter, and
the magnitude w of the projection of an arbitrary 3D vector in units of the modulus w3D of the latter, and 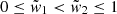 . In the present calculations no account is taken of the possibility that attenuation by dust, and therefore viewing angle, can limit the observable phase of AGN to a fraction of their intrinsic lifetimes (Hopkins et al. 2005; but see Capelo et al. 2017).
. In the present calculations no account is taken of the possibility that attenuation by dust, and therefore viewing angle, can limit the observable phase of AGN to a fraction of their intrinsic lifetimes (Hopkins et al. 2005; but see Capelo et al. 2017).
Last but not least, our DAGN model included a tunable parameter ϵagn defined as
that measures both the effectiveness of single AGN triggering and the simultaneity of the activity of the two central BH at each timestep i. It is ultimately a measure of the detectability of correlated nuclear activity with values ranging from 0 to 1 that encompass, respectively, the two most extreme possibilities: i) totally ineffective triggering; and ii) fully effective triggering and fully correlated activity. Some hydrodynamic simulations of galaxy mergers indicate that simultaneous BH activity requires similarly massive progenitors (Blecha et al. 2013; Steinborn et al. 2016), while others suggest that the degree of correlation could be related to the activity strength, in the sense that it decreases with increasing luminosity (e.g. Van Wassenhove et al. 2012). In any case, for the present exercise we have kept the value of this parameter always equal to one whenever the conditions for DAGN activity are fulfilled, implying that we will be obtaining probability estimates that operate as upper limits. Let us note that by proceeding in this way the comparison of our outcomes with observations can be used, for instance, to constrain the degree of correlation in the shinning of AGN in pairs provided it is assumed that the triggering of BH activity is highly effective.
4. Probabilities of DAGN
One of the most important outcomes of any investigation on the connection between dual BH activity and mergers is the incidence of DAGN represented by the fraction of these systems out of interacting systems.
4.1. Definitions
Determination of the number of physically bound galaxy pairs in a region or epoch of the universe is by no means simple. As a result, most theoretical studies choose to calculate the incidence of DAGN by measuring instead the fraction of the total encounter time the pairs of active galaxies satisfy certain conditions. This implies invoking the ergodic hypothesis and replacing the ensemble average over of all the system’s states in its phase space by temporal averages. In other words, assuming that by observing a binary merger for long enough time one has access to many realizations of the system4.
This is also the view adopted in the present work. In the first place, we show results for two probabilities that normalize the dual activity time to what would be the most natural measure of the length of the merger phase, the merger timescale, τmer, a quantity which has a relatively standardized definition in numerical simulations (see e.g. Solanes et al. 2018, and references therein, as well as Sect. 2). They are:
1. Pdagn, which provides, for each and every one of our mergers, an estimate of the fraction of the total merger time in which dual BH activity, observable or not, is feasible, offering therefore a measure of the intrinsic abundance of DAGN predicted by the major merger scenario; and
2. Pdagn, spec, which only considers the dual-activity time when the BH are observable through double-peaked narrow line features, thus providing an estimate of the frequency of DAGN that could be detected with optical spectroscopy in surveys free of other limitations.
These probabilities can be expressed mathematically as
where the sums go over all n timesteps in which τmer is divided in our simulations and where pobs(i) measures the probability of DAGN detection calculated with the aid of Eqs. (4) and/or (5) for a given set of observational constraints.
The inherent difficulties that observational studies must face when identifying physically bound pairs of AGN, especially at large separations, lead them frequently to constrain the characterization of the abundance of DAGN in subsets of close pairs selected by applying certain specific spatial and/or kinematic filters. In order to facilitate the comparison of our predictions with this kind of results, and with those from theoretical studies inferred along the same lines, we have also inferred the following estimates for the fraction of DAGN that take into account the amount of merger time in which the intercentric separation of the galaxies falls within the different (projected) phase-space thresholds set out in the previous section to define galaxy pairs:
3. 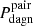 , which gives the probability that a DAGN is included in a catalog of binaries; and
, which gives the probability that a DAGN is included in a catalog of binaries; and
4. 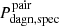 , which measures the fraction of DAGN that can be expected to satisfy simultaneously the visibility constraints arising from the phase-space filtering applied for the selection of galaxy pairs and the double peak-method.
, which measures the fraction of DAGN that can be expected to satisfy simultaneously the visibility constraints arising from the phase-space filtering applied for the selection of galaxy pairs and the double peak-method.
In mathematical form:
where fcat is the total fraction of the merger time of a bound galaxy pair during which it is expected to be included in a given catalog of binaries, while pcat(i) and pcatobs(i) measure, respectively, the probabilities at the ith timestep that a merging system fulfills the conditions for being considered a galaxy pair and at the same time being detected as a DAGN.
The individual estimates of the above four probabilities that arise from our suite of major-merger runs are displayed graphically. The results for Pdagn and Pdagn, spec are shown in Figs. 1–3, while, because of their length, those for 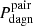 and
and 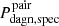 are shown in a series of plots (Figs. B.1–B.6) in Appendix B. In the panels of all these figures each single estimate of the fractional incidence of DAGN is represented by a green dot, while the large open red symbols and associated error bars show the location (median) and scale (interquartile range) of the subsets of results corresponding to the three different initial orbital eccentricities considered in our merger runs. The values of these estimators are listed in Table 2, as well as in the Table A.1. We note that the latter table only contains the probabilities for the core runs (rcirc, p = 4/3). The average frequencies for mergers with rcirc, p = 2.0 are presented exclusively in graphic form in Figs. B.5 and B.65.
are shown in a series of plots (Figs. B.1–B.6) in Appendix B. In the panels of all these figures each single estimate of the fractional incidence of DAGN is represented by a green dot, while the large open red symbols and associated error bars show the location (median) and scale (interquartile range) of the subsets of results corresponding to the three different initial orbital eccentricities considered in our merger runs. The values of these estimators are listed in Table 2, as well as in the Table A.1. We note that the latter table only contains the probabilities for the core runs (rcirc, p = 4/3). The average frequencies for mergers with rcirc, p = 2.0 are presented exclusively in graphic form in Figs. B.5 and B.65.
 |
Fig. 1. Expected incidence of dual active BH in equal-mass mergers of spiral galaxies (of Sb type) in the nearby universe, as a function of the merger timescale, τmer. Pdagn is the intrinsic fraction of binary mergers with active BH pairs and Pdagn, spec is the fraction of these mergers observable through double-peaked narrow line features in the optical window. The panels on each column show results for different representative thresholds of nuclear activity (see text). Top panels: results for a BH lifetime, τagn, of 102 Myr, while bottom panels: results for τagn = 10 Myr. Individual predictions are represented with green dots, while large red open circles and error bars show the median and interquartile range of the subsets of results inferred from the same initial orbital eccentricity, ϵ, which increases from left to right in each panel. This figure is for mergers starting with a reduced orbital energy rcirc, p = 4/3. |
 |
Fig. 3. Same as Fig. 1 but for equal-mass Sb+Sb mergers with an initial reduced orbital energy rcirc, p = 2.0. |
Medians (M), lower (Q1), and upper (Q3) quartiles of the DAGN fraction predicted by the major merger scenario at z ∼ 0.
4.2. Results
In the next section we shall compare our data to other theoretical and observational studies. We first summarize our main findings regarding the values and behavior of the different probabilities for DAGN just defined and their dependence on the main parameters controlling the length of mergers, namely, the initial orbital ellipticity and energy, the mass ratio, and the spin and relative orientations of the galaxies.
1. There is a mild negative correlation of Pdagn with the initial orbital circularity and the level of activity, more evident for 3:1 mass ratios (top three panels of each six-panel group in Figs. 1–3). For equal-mass mergers, the medians of the different samples of Pdagn inferred for the LONG BH duty-cycle reach up to ∼7–9% for (moderately) radial collisions and WEAK/INTERMEDIATE luminosities, while for the Sb+Sc pairs this percentage raises up to ∼13% for the most radial and less powerful DAGN, with some individual predictions approaching 20%. As expected, the decrease of the BH duty-cycle reduces the values of this probability significantly, moving the medians toward ∼4–5% for the WEAK activity regime and toward clearly lower frequencies for the INTERMEDIATE and STRONG regimes. Indeed, in this latter case, the median values of Pdagn become negligible independently of the initial orbital parameters, the progenitors’ mass ratio or the length of the BH duty-cycle.
2. Comparison of the previous results with the bottom three panels of each six-panel group in Figs. 1–3 shows that Pdagn, spec behaves similarly. As in the case of Pdagn, we observe a weak dependency of this probability on the orbital characteristics, in the form of a tendency for more circular orbits to lead to lower typical abundances. This is also true for the mass ratio, despite the considerable increase in the merger times that it entails. Again, the highest characteristic values of Pdagn, spec, now in the range ∼0.5–1.3%, are obtained for the lowest X-ray threshold, while not one of our hundreds of mergers leads to probabilities above 2%.
In the STRONG regime (right-hand panels of Figs. 1 and 2), where it is not surprising to find null values of Pdagn, spec, the spread of the individual predictions inferred for the LONG BH duty-cycle is substantial and anticorrelated with the orbital circularity. For the most radial orbits we recorded quite a number of results falling in the neighborhood of the interval 0.5–1.5%, while we barely obtain values above 0.5% in the runs where ϵ = 0.7. Much like Pdagn, we also see that the SHORT BH duty-cycle leads to a reduction in the location and scale of the distributions of values of Pdagn, spec, except in the case of the less powerful DAGN in 3:1 mergers, which do not seem particularly affected by changes in the duration of the periods of activity (compare the bottom left panels of the two six-panel groups in Fig. 2). This indicates that these mergers, regardless of the orbital configuration, hardly lead to isolated DAGN episodes, so that once the conditions for WEAK activity are satisfied they continue to hold until the end of the merger process.
3. In equal-mass mergers both Pdagn and Pdagn, spec are independent of the modulus and orientation of the progenitors’ halo spin. However, for 3:1 mergers, especially those taking place along elliptical orbits, these two probabilities tend to be positively correlated with the length of the merger phase, which in turn increases with the angular separation between the spin of the principal halo and the orbital spin (see e.g. Solanes et al. 2018) as collisions go from direct to retrograde.
4. Contrary to Pdagn and Pdagn, spec, the probabilities that take into account the activity time spent within a given projected separation do not appear to correlate with the initial orbital circularity of the mergers (see Table A.1). As expected, the more restrictive the separation criteria used in the normalization of 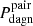 and
and 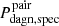 the larger their values, while the opposite is true for both the luminosity threshold and the length of the activity cycle of the BH (the dependence on the mass ratio shows no discernible global trend).
the larger their values, while the opposite is true for both the luminosity threshold and the length of the activity cycle of the BH (the dependence on the mass ratio shows no discernible global trend).
We also find that the WIDE and CLOSE filterings lead to identical results for 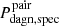 independently of the power emitted by the BH. This happens because they define pairs with no limitations in the minimum spatial separation, so the main restriction to the observability of DAGN comes from the low-velocity constraint imposed by the double-peak method (see the middle and right bottom panels of each six-panel group in Figs. B.1–B.6). In contrast, both
independently of the power emitted by the BH. This happens because they define pairs with no limitations in the minimum spatial separation, so the main restriction to the observability of DAGN comes from the low-velocity constraint imposed by the double-peak method (see the middle and right bottom panels of each six-panel group in Figs. B.1–B.6). In contrast, both 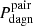 and
and  are substantially reduced for the OPEN filter (see left bottom panels), to the point that just in a small number of instances involving elongated orbital encounters and long-term dual activity, it is feasible to first select and then observe double-peak narrow emission lines at peak luminosities with a non-zero probability. The fact that in this case we filtered out small separations makes the outcomes insensitive to AGN pairs in an advanced state of merger.
are substantially reduced for the OPEN filter (see left bottom panels), to the point that just in a small number of instances involving elongated orbital encounters and long-term dual activity, it is feasible to first select and then observe double-peak narrow emission lines at peak luminosities with a non-zero probability. The fact that in this case we filtered out small separations makes the outcomes insensitive to AGN pairs in an advanced state of merger.
5. The top six-panel groups in Figs. B.1–B.6 show that for WEAK (Lbol ≳ 1042 erg s−1) DAGN with τagn = 100 Myr the medians of 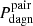 fall in the ranges ∼10–15%, ∼15–25% and ∼35–50%, as one moves from OPEN, to WIDE, and then to CLOSE separations, respectively (the upper limits corresponding to 3:1 mergers), while the change from the LONG BH duty-cycle to the SHORT one reduces them approximately to the half. On the other hand,
fall in the ranges ∼10–15%, ∼15–25% and ∼35–50%, as one moves from OPEN, to WIDE, and then to CLOSE separations, respectively (the upper limits corresponding to 3:1 mergers), while the change from the LONG BH duty-cycle to the SHORT one reduces them approximately to the half. On the other hand, 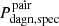 shows under the same circumstances medians within ∼0.5–1.5% for the WIDE and CLOSE filters and always below 0.5% in the OPEN case. Moreover, for the most luminous DAGN we predict short characteristic visibility periods with all normalizations, particularly those corresponding to the OPEN filter, for which we find null medians in all cases investigated (bottom six-panel groups of Figs. B.1–B.6).
shows under the same circumstances medians within ∼0.5–1.5% for the WIDE and CLOSE filters and always below 0.5% in the OPEN case. Moreover, for the most luminous DAGN we predict short characteristic visibility periods with all normalizations, particularly those corresponding to the OPEN filter, for which we find null medians in all cases investigated (bottom six-panel groups of Figs. B.1–B.6).
For its part, the dispersion of the predicted probabilities tends to increase with increasing orbital elongation, the physical closeness of the pairs, and the progenitors mass ratio, being particularly sensitive to the BH lifetime (all this for the same initial orbital energy; see also point #6 below). We note however that, as in the case of Pdagn and Pdagn, spec for equal-mass mergers, there does not seem to be any clear correlation between the individual scores of 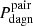 and
and 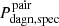 and the internal spin of the galaxies, regarding both its initial magnitude and direction, and with the relative orientation of the latter with respect to the orbital spin (see also Capelo et al. 2017). This means that it is not easy for numerical investigations of DAGN relying on idealized binary mergers to foresee a priori the minimum number of orbital configurations needed to correctly represent the whole plot of possible results.
and the internal spin of the galaxies, regarding both its initial magnitude and direction, and with the relative orientation of the latter with respect to the orbital spin (see also Capelo et al. 2017). This means that it is not easy for numerical investigations of DAGN relying on idealized binary mergers to foresee a priori the minimum number of orbital configurations needed to correctly represent the whole plot of possible results.
6. Changes in the initial orbital energy of mergers within the limits set out in Sect. 4.1 essentially leave the previous conclusions unchanged (compare Figs. B.1 and B.2 with B.5 and B.6, respectively), despite corresponding to a variation of up to 50%.
5. Validation of the results
The validation of our results throughout the comparison with observations is not at all straightforward due to the tendency of AGN surveys to be affected by selection biases and incompleteness, the lack of a unified estimator of the abundance of dual systems, and the uncertainties of the measurements, which are frequently based on small datasets. The latter problems affect simulations as well.
To aid clarity in this section we have included two summary figures, which provide a direct comparison of the global results of our numerical model for DAGN triggering via major mergers with the observational results and other theoretical predictions. Figure 4 shows the two probabilities that normalize the dual activity time to the total length of the merger phase, while Fig. 5 shows the probabilities calculated taking into account the abundance of DAGN in different subsets of close pairs defined through thresholds in phse space.
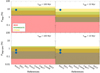 |
Fig. 4. Comparison of our results for Pdagn (top) and Pdagn, spec (bottom) with observations and other theoretical predictions. The total ranges of plausible values for these probabilities inferred from all the major mergers in our suite, i.e. regardless of the orbital eccentricity, orbital energy and mass ratio of the progenitor galaxies, are represented by means of horizontal bands color coded to show the different thresholds of the bolometric X-ray luminosity adopted in our numerical DAGN model (see the inset in the top-left panel). The panels on each column depict results for different durations of the AGN phase, τagn: 100 Myr (left) and 10 Myr (right). Distributed between this figure and Fig. 5, we show a set of benchmarks formed by the individual values and/or ranges of values quoted in the observational works by Rosario et al. (2011, Ros11), Ellison et al. (2011, Ell11), Silverman et al. (2011, Sil11) and Koss et al. (2012, Kos12), which are represented by blue solid circles, those corresponding to our own estimates based on the large AGN surveys by Comerford et al. (2009, Com09) and Ge et al. (2012, Ge12), represented by blue solid squares, as well as those stemming from the cosmological simulations by Rosas-Guevara et al. (2019), Volonteri et al. (2016) and Steinborn et al. (2016) that we group under the same label (Cosmo), and from the isolated merging runs of Capelo et al. (2017, Cap17), which are identified by red solid circles. |
 |
Fig. 5. Same as Fig. 4 but for the probabilities |
5.1. Comparison with observations
One of the few observational studies providing measurements of the incidence of DAGN relatively close to those defined in Sect. 4.1 is that by Rosario et al. (2011). These authors, starting from a small sample of (12) imaged AGN with a median z = 0.35, conclude that the “global” fraction of double-peaked emitters on kpc-scale pairs should be in the range 0.3–0.65%. This result shows a more-than-fair agreement with the total range of individual scores we obtain for Pdagn, spec in our simulations, which go from zero to 2%, provided we assume, as they do, that there has not been major evolution in the population of AGN between z ∼ 0 and z ∼ 0.4. In addition, Rosario et al. (2011) apply population statistics to deliver a rough estimate of the fraction of time a merging pair of galaxies spends in a QSO phase under the assumption that all QSO are associated with a major merger event. Their calculation of 8% is entirely in line with the medians of Pdagn we infer for the WEAK and INTERMEDIATE activity levels.
Ellison et al. (2011) directly measure the DAGN fraction in a large sample of more than 11 000 galaxy pairs extracted from the SDSS legacy volume, where companionship is defined from the constraints Δr2D < 80 kpc and ΔvLOS < 200 km s−1. From the information gleaned from the Kewley et al. (2001) BPT classification scheme, they find that this fraction increases steadily with decreasing nuclear distance up to ∼10% at the closest separations (Δr2D < 10 kpc) for major pairs – this number doubles when they consider pairs with AGN that are either single or double. By using our estimates of 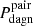 for low-luminosity (WEAK) DAGN in WIDE pairs as a proxy for this quantity (and ignoring the differences in our respective velocity constraints), we find that the best agreement – which is actually quite good – is provided by our predictions corresponding to the SHORT BH duty-cycle. In contrast, for the LONG BH duty-cycle we infer typical fractions in the range ∼15–25% and individual values that never fall below 12%.
for low-luminosity (WEAK) DAGN in WIDE pairs as a proxy for this quantity (and ignoring the differences in our respective velocity constraints), we find that the best agreement – which is actually quite good – is provided by our predictions corresponding to the SHORT BH duty-cycle. In contrast, for the LONG BH duty-cycle we infer typical fractions in the range ∼15–25% and individual values that never fall below 12%.
The results of Ellison et al. (2011) are corroborated by Silverman et al. (2011), who find a qualitatively similar evolution of the fraction of moderate-luminosity (Lbol ∼ 1043 erg s−1) AGN with projected physical distance using close pairs (Δr2D ≤ 75 kpc and ΔvLOS < 500 km s−1) of massive galaxies (Mstar > 2.5 × 1010 M⊙) identified in the zCOSMOS 20k catalog (Lilly et al. 2007). Similarly to the former work, they provide measures divided according to mass ratio (though actually only for global values because their sample is smaller). Thus, according to Silverman et al. (2011), the median fraction of galaxy pairs with a mass ratio less than 3:1 hosting AGN is 11.7 ± 3.2%. Interestingly, this value is remarkably close to the median of 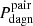 we obtain for WIDE pairs of INTERMEDIATE activity and, in this case, LONG BH duty-cycles. It must be kept in mind, however, that this result is inconclusive, as the observational values provided by Silverman et al. (2011) are likely overestimates, because they both do not differentiate between galaxy pairs with single or double AGN and correspond to redshifts 0.25 < z < 1.05 in which gas-rich mergers are expected to be considerably more frequent than today. We also note that this survey, as the previous one, is deficient in late-stage mergers.
we obtain for WIDE pairs of INTERMEDIATE activity and, in this case, LONG BH duty-cycles. It must be kept in mind, however, that this result is inconclusive, as the observational values provided by Silverman et al. (2011) are likely overestimates, because they both do not differentiate between galaxy pairs with single or double AGN and correspond to redshifts 0.25 < z < 1.05 in which gas-rich mergers are expected to be considerably more frequent than today. We also note that this survey, as the previous one, is deficient in late-stage mergers.
Koss et al. (2012) study in turn the fraction of DAGN from a sample of 167 nearby (z < 0.05) ultra-hard X-ray-selected AGN of the all-sky Swift Burst Alert Telescope survey. The good thing about this work is that it not only identifies the fraction of these AGN having at least one companion within 100 kpc, but provides detailed information on the X-ray luminosities of the pairs, their mass ratios and their projected separation. By examining these data (see the online-only version of their Table 1) one can deduce, for instance, that the frequency of DAGN with Lbol ∼ 1042 erg s−1 in major pairs at projected separations < 30 kpc is about 40% (10/24)6. As in the previous cases, this observational result is also remarkably in line with our calculations, which on this occasion are those associated with 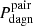 for WEAK sources in CLOSE pairs. We find the best agreement for the estimates that assume a LONG BH duty-cycle, in which Koss et al.’s result fits perfectly well, while our predictions for the SHORT BH lifetime are on average a factor of ∼1.5–2 smaller. Nevertheless, we caution that as with the work of Silverman et al. (2011), we can only establish an approximated comparison, given that they consider pairs in which there is always an active nucleus, a circumstance not included in our normalization for
for WEAK sources in CLOSE pairs. We find the best agreement for the estimates that assume a LONG BH duty-cycle, in which Koss et al.’s result fits perfectly well, while our predictions for the SHORT BH lifetime are on average a factor of ∼1.5–2 smaller. Nevertheless, we caution that as with the work of Silverman et al. (2011), we can only establish an approximated comparison, given that they consider pairs in which there is always an active nucleus, a circumstance not included in our normalization for 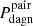 and that raises their estimates by an amount that is difficult to gauge.
and that raises their estimates by an amount that is difficult to gauge.
We have also attempted to extend this comparison to DAGN studies based on samples extracted from large catalogs of individual galaxies. This is the case, for instance, of Comerford et al. (2009), who examine 1881 red galaxies from the DEEP2 Galaxy Redshift Survey, and of Ge et al. (2012), who draw a parent AGN sample from the nearly million objects that constitute the extragalactic spectroscopic survey of the SDSS-DR7. In such instances, there is the possibility of using the local value of the fraction of massive galaxies having a similarly large companion within a projected separation of 30 kpc given in Man et al. (2012) (0.07 ± 0.04) to convert the fractions of spectroscopically detected duals into frequencies that can represent a reasonable proxy for our estimates of 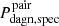 for CLOSE pairs and WEAK emission (this conversion only makes sense if one assumes that major mergers are behind all AGN fueling). The application of this simple rescaling suggests that the observed fractions of spectroscopically detected duals in tight galaxy pairings should be around 1.5% and 1.3%, respectively. These percentages, as well as being consistent with each other, are in very good agreement with our predictions.
for CLOSE pairs and WEAK emission (this conversion only makes sense if one assumes that major mergers are behind all AGN fueling). The application of this simple rescaling suggests that the observed fractions of spectroscopically detected duals in tight galaxy pairings should be around 1.5% and 1.3%, respectively. These percentages, as well as being consistent with each other, are in very good agreement with our predictions.
5.2. Comparison with simulations
We now compare our results with estimates arising from some of the most recent numerical studies that look into the abundance of DAGN, either from cosmological simulations including full hydrodynamics, or from controlled binary merger experiments like ours, but with a explicit gaseous component.
Rosas-Guevara et al. (2019) employ a cosmological simulation in the largest comoving volume (100 Mpc)3 from the EAGLE project (Schaye et al. 2015) running it up to z = 0. They consider a visible DAGN to be an active BH pair with a (intrinsic) separation < 30 kpc powering at Lbol ≳ 1043 erg s−1. However, instead of normalizing the dual-activity time to the total time spent below that separation, they choose to define the probability of detecting DAGN only in the hard X-ray bands as the average fraction of these objects with respect to the total number of AGN and calculate it at different cosmic epochs. At z = 0.0–0.5 they find the fraction of dual systems in which at least one of the AGN is visible in the hard X-ray band to be about 0.5%. As these authors point out, their prediction is broadly consistent with similarly-defined probabilities inferred from the outcomes of the cosmological hydrodynamic simulation Horizon-AGN by Volonteri et al. (2016), and of an even larger volume simulation included in the Magneticum Pathfinder set by Steinborn et al. (2016). These two studies also find that DAGN constitute less than 0.5% of all AGN, though in the second case the estimate corresponds to z = 2. All these results fall considerably short of both what is inferred from observations – Koss et al. (2012) find, for instance, that the DAGN fraction defined in this way, but detected using both X-ray spectroscopy and emission lines diagnostics, is ∼8% at scales < 30 kpc – and our estimates of 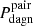 for INTERMEDIATE DAGN in CLOSE pairs. If we ignore for a moment that the definition of the fraction of visible DAGN used in Rosas-Guevara et al. (2019) is hardly consistent with our definition of
for INTERMEDIATE DAGN in CLOSE pairs. If we ignore for a moment that the definition of the fraction of visible DAGN used in Rosas-Guevara et al. (2019) is hardly consistent with our definition of 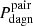 , a plausible explanation for this strong discrepancy would be the limited effectiveness of correlated nuclear activity that characterizes AGN in cosmological simulations. According to Rosas-Guevara et al. (2019) there is a probability of only 3% that two paired AGN are simultaneously detected, in other words that they are turned on at the same time, when they have a separation < 30 kpc, which they attribute to the presence of rapid (on temporal scales of Myr) AGN variability. It is curious to note, however, that if we had reduced the effectiveness of the dual nuclear activity adopted in our simulations from 1.0 to 0.03, then the bulk of our predictions for this probability would have fall between 0.2 and 1%, in much better agreement with the cosmological outcomes. In contrast, the comparison of our results with the observations carried out in Sect. 5.1 points to effectiveness close to 100%.
, a plausible explanation for this strong discrepancy would be the limited effectiveness of correlated nuclear activity that characterizes AGN in cosmological simulations. According to Rosas-Guevara et al. (2019) there is a probability of only 3% that two paired AGN are simultaneously detected, in other words that they are turned on at the same time, when they have a separation < 30 kpc, which they attribute to the presence of rapid (on temporal scales of Myr) AGN variability. It is curious to note, however, that if we had reduced the effectiveness of the dual nuclear activity adopted in our simulations from 1.0 to 0.03, then the bulk of our predictions for this probability would have fall between 0.2 and 1%, in much better agreement with the cosmological outcomes. In contrast, the comparison of our results with the observations carried out in Sect. 5.1 points to effectiveness close to 100%.
We additionally include in this appraisal the recent hydrodynamic simulations of isolated mergers by Capelo et al. (2017). These authors have build a suite of 12 simulated mergers (six of them major) and calculated dual-activity observability timescales assuming different thresholds for the bolometric luminosity, adopting different separation filters and, no less important, translating their 3D outcomes into projected quantities, as we have done too. In particular, in Table 2 of their paper they list the individual frequencies for DAGN with Lbol ≳ 1043 erg s−1 at projected separations larger than both 1 kpc and 10 kpc normalized to the merger time delimited by the filtering (in an attempt to account for the constraints associated with DAGN detection via spectroscopy they also apply a ΔvLOS ≥ 150 km s−1 filter that, however, lacks a maximum threshold for the projected intercentric distance, thus preventing a fair comparison with our data). Since they consider interacting systems with separations starting at ∼90 kpc, it is acceptable to contrast their figures with our estimates of 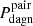 for, respectively, WIDE and OPEN pairs in the INTERMEDIATE luminosity regime. At this level of activity, our predicted median frequencies – taking into account the different BH duty-cycles, mass ratios and orbital energies assumed – range between ∼4–16% for the WIDE filter and between ∼0.5–9% for the OPEN one, whereas the respective normalized times for the simulated major encounters of Capelo et al. (2017) vary from ∼4% to 14% and from ∼1% to 9%. The high degree of consistency shown by both sets of results can be described as more than remarkable, especially when one takes into account that our simulations do not contain an explicit hydrodynamic component.
for, respectively, WIDE and OPEN pairs in the INTERMEDIATE luminosity regime. At this level of activity, our predicted median frequencies – taking into account the different BH duty-cycles, mass ratios and orbital energies assumed – range between ∼4–16% for the WIDE filter and between ∼0.5–9% for the OPEN one, whereas the respective normalized times for the simulated major encounters of Capelo et al. (2017) vary from ∼4% to 14% and from ∼1% to 9%. The high degree of consistency shown by both sets of results can be described as more than remarkable, especially when one takes into account that our simulations do not contain an explicit hydrodynamic component.
6. Summary and concluding remarks
A physically motivated numerical model for DAGN triggering based on a large subset of the nearly six hundred collisionless simulations of major mergers presented in Solanes et al. (2018) has been used to predict the visibility of these systems. Our intention has been to shed light on the apparent inconsistency between what observations and theory say in this regard if, as is suspected, there is a more than probable causal connection between galaxy collisions and dual nuclear activity (Shen et al. 2010; Koss et al. 2012). The 432 bound S+S pairs selected for this task encompass a wide range of merger parameters (initial geometry and energy of the encounters, mass ratio, and halo spins) covering a good number of scenarios representative of the gravitational interactions between galaxies expected to lead to DAGN activation. The ansatz at the basis of our investigation is that it is feasible to study the essential aspects of the major-merger-driven scenario for DAGN by replacing the complex gas physics involved in the fueling of nuclear activity by limits on the separation in phase space of the central regions of the colliding objects. The most outstanding feature of such treatment is that it enables the obtention of sets of experiments large enough to permit the statistical assessment of the role played by the parameters governing dual activity, as well as the easy and intuitive inclusion of constraints in projected distance and velocity that mimic the most frequent observational limitations of AGN surveys, thus facilitating the calculation of predictions directly comparable with the existing data. The simplicity of our modeling is therefore its main strength since, at present, the realization of full hydrodynamic simulations capable of resolving in detail a similarly large number of galaxy mergers while also addressing the feeding, growing and feedback of the nuclear SMBH is still prohibitive.
Certainly, there are also some caveats implied by our procedure. The most important being that the exclusion of the explicit treatment of the gas physics does not allow following the evolution of the AGN in a self-consistent way. This simplification hinders the applicability of our model to the study of a single encounter, but it should correctly describe, in a statistical way, the collective effects of a large number of them. Thus, it seems reasonable to expect that the results we have inferred in this work will still hold when the realization of extensive studies capable of adopting a fully realistic picture of the SMBH pairing becomes feasible. The good general agreement obtained between our predictions and the outcomes of both observations and other theoretical works can be considered as an endorsement of this expectation.
Overall, the present work shows that the inconsistency between the expected fraction of galaxy pairs undergoing synchronized nuclear activity – inferred from arguments based on the hierarchical build-up of structure – and the order-of-magnitude-lower abundance of spectroscopic DAGN often reported by observations (Yu et al. 2011) is, in a good measure, only apparent. More specifically, our calculations provide a reasonable explanation for coexistence, in a scenario where major mergers trigger the activity of the central BH of galaxies, of theoretical predictions that place the intrinsic frequency of DAGN at levels on the order of 10% (e.g. Volonteri et al. 2003), and of nearby AGN surveys based on emission-line diagnostics, which systematically find fractions of double-peaked narrow-line systems at kpc-scales around 1% or lower (e.g. Rosario et al. 2011). Since the AGN phenomenon involves short-range galaxy interactions, it has also been proven that the most radical observational limitations in the detection of dual activity are those that cause a deficit in the number of very close companions (intercentric distances ≲ few kpc).
On the other hand, our merger simulations further reveal that peak values of accretion and dual BH activity, that we tentatively associate with values of Lbol higher than 1044 erg s−1, should be rather difficult to observe in galaxy pairs. This would not result only from the inherent difficulty that involves identifying dual systems with small spatial offsets, but also from the fact that, whatever the orbital configuration of the merger, the required physical conditions are always reached shortly before the formation of the remnant and the subsequent SMBH binary (a bound pair of SMBH at scales of a few pc). Our results point to intrinsic frequencies (Pdagn) of high-luminosity DAGN that all too often fall below 1%, with the majority of merger configurations actually leading to null values – the detection probabilities in close pairs, 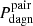 and
and 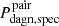 , also tend to be very small, except when the most restrictive imaging filters, in other words, those with Δr2D ≤ 30 kpc, are applied. We also independently confirm previous findings from both theoretical and observational studies that variations of certain factors that control the length of mergers, such as the initial orbital geometry or the mass ratio of the galaxies, can change the likelihood of DAGN detection (e.g. Ellison et al. 2011; Capelo et al. 2017). Other factors, however, such as the initial energy of mergers, seem to play a secondary role.
, also tend to be very small, except when the most restrictive imaging filters, in other words, those with Δr2D ≤ 30 kpc, are applied. We also independently confirm previous findings from both theoretical and observational studies that variations of certain factors that control the length of mergers, such as the initial orbital geometry or the mass ratio of the galaxies, can change the likelihood of DAGN detection (e.g. Ellison et al. 2011; Capelo et al. 2017). Other factors, however, such as the initial energy of mergers, seem to play a secondary role.
The fact that our experiments do not explicitly address the physics of the BH does not prevent us from drawing a few tentative conclusions in this regard through the comparison of our outcomes with those of previous works. The first has to do with the typical duration of the activity phase of the SMBH, for which we have found marginal evidence in favor of the longer-lasting periods of about 100 Myr, especially if we take into account that all our estimates are upper limits. We have also found indications that the activity of the central BH could be highly correlated, given that those comparisons between our estimates and other works that suggest otherwise can be attributed to significant differences in the way in which the visibility of the DAGN is defined. It is precisely this heterogeneity in establishing DAGN abundances, often conditioned by the particular characteristics of the available data, that results in obstacles for an efficient comparison between theory and observations, or between the observations themselves, forcing us to follow a more qualitative than quantitative approach. Undoubtedly, the standardization of the measure of the DAGN fraction is something much needed in the efforts toward making a better use of the available information. However, there is little point in implementing a standard estimator of a property if it cannot be applied onto complete datasets. This is indeed the factor that most distorts the observational outcomes, as we have already mentioned in several points of this paper. Obtaining a complete sample of AGN is complicated since it is very difficult to quantify the biases. Even the same dataset can yield mixed results depending on the wavelength, resolution and sensitivity with which observations are conducted. In particular, there is growing evidence that black holes are likely to become heavily obscured behind merger-driven gas and dust, especially in the final merger stages when the two galactic nuclei are separated by just a few kiloparsecs (Koss et al. 2018).
In summary, it has been shown that we need look no further than the most frequent photometric and spectroscopic constraints involved in the detection of DAGN to reconcile the theoretical merger rate of galaxies predicted in a hierarchical ΛCDM universe with the paucity of close AGN pairs systematically observed in the local volume. It has not been necessary to resort to the uncorrelated shining of the AGN, linked perhaps to a high variability in the accretion rates, or to a low efficiency in the triggering of the nuclear activity. In addition, no account has been taken of the many other factors that could disturb the observed frequency of AGN pairs, either by decreasing it, such as merger-driven obscuration or the tendency reported for active galaxies at small separations (i.e., in late-stage mergers) to be detected only in X-rays (Koss et al. 2012; Satyapal et al. 2014; Blecha et al. 2018), or by increasing it, such as the “false positives” produced by double-peaked narrow-line emission associated with jets or outflows from a single AGN (Shangguan et al. 2016; Liu et al. 2018). Therefore, by reducing the tension between observations and theoretical predictions arising from the current cosmological framework, the results of the present work reinforce the support for the major merger scenario as a plausible contender among the various mechanisms that may be responsible for powering DAGN. Even so, in no way they should be taken as a confirmation that gravitational interactions, in the form of major galaxy collisions, are necessarily the single physical process capable of driving the interstellar gas to the central regions of these objects and fueling their nuclear SMBH.
In line with this approximation, our experiments neglect the slight reduction on the dynamical friction timescale that may result in moderately wet mergers (i.e. with gas fractions on the order of 10%) from the cooling of the gas, which acts to enhance the central mass concentration of the galaxies, and favors the sinking of the secondary object onto the primary one (see Colpi 2014 and references therein.)
30 kpc is also the approximate physical scale in projected separation on which galaxy in pairs start to exhibit significantly higher star formation rates than field galaxies (Barton et al. 2000; Lambas et al. 2003; Alonso et al. 2004; Nikolic et al. 2004; Perez et al. 2006).
One necessary condition that must be met for this to hold is that the orbital planes and relative orientations of the galaxy pairs have to be roughly isotropically distributed (Khochfar & Burkert 2006).
Acknowledgments
The authors acknowledge financial support from the Spanish AEI and European FEDER funds through the coordinated research project AYA2016-76682-C. J.M.S. and J.D.P., as well as I.M., extend their gratitude to the Program for Promotion of High-Level Scientific and Technical Research of Spain under contracts AYA2013-40609-P and AYA2013-42227-P, respectively. C.R.A. acknowledges the Ramón y Cajal Program of the Spanish Ministry of Economy and Competitiveness through project RYC-2014-1577. Additional funding has been provided by the State Agency for Research of the Spanish MCIU through “Center of Excellence Severo Ochoa” awards for the Instituto de Astrofísica de Andalucía and for the Instituto de Astrofísica de Canarias, and through a “Center of Excellence María de Maeztu” award to the Institut de Ciències del Cosmos.
References
- Alonso, M. S., Tissera, P. B., Coldwell, G., & Lambas, D. G. 2004, MNRAS, 352, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Barton, E. J., Geller, M. J., & Kenyon, S. J. 2000, ApJ, 530, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J. 2005, MNRAS, 358, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Bessiere, P. S., Tadhunter, C. N., Ramos Almeida, C., & Villar Martín, M. 2012, MNRAS, 426, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, L., Loeb, A., & Narayan, R. 2013, MNRAS, 429, 2594 [NASA ADS] [CrossRef] [Google Scholar]
- Blecha, L., Snyder, G. F., Satyapal, S., & Ellison, S. L. 2018, MNRAS, 478, 3056 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, S. E., Kay, S. T., Duffy, A. R., et al. 2013, MNRAS, 429, 3316 [NASA ADS] [CrossRef] [Google Scholar]
- Capelo, P. R., Dotti, M., Volonteri, M., et al. 2017, MNRAS, 469, 4437 [NASA ADS] [CrossRef] [Google Scholar]
- Cisternas, M., Jahnke, K., Bongiorno, A., et al. 2011, ApJ, 741, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M. 2014, Space Sci. Rev., 183, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., & Dotti, M. 2011, Adv. Sci. Lett., 4, 181 [CrossRef] [Google Scholar]
- Comerford, J. M., Gerke, B. F., Newman, J. A., et al. 2009, ApJ, 698, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Comerford, J. M., Pooley, D., Gerke, B. F., & Madejski, G. M. 2011, ApJ, 737, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Darg, D. W., Kaviraj, S., Lintott, C. J., et al. 2010, MNRAS, 401, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 2000, ApJ, 536, L39 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ellison, S. L., Patton, D. R., Mendel, J. T., & Scudder, J. M. 2011, MNRAS, 418, 2043 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Mendel, J. T., Patton, D. R., & Scudder, J. M. 2013, MNRAS, 435, 3627 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, L., Han, Y., Fang, G., et al. 2016, ApJ, 822, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman, G., Volonteri, M., & Dotti, M. 2009, ApJ, 693, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Myers, A. D., Djorgovski, S. G., & Yan, L. 2011, ApJ, 733, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Wrobel, J. M., Myers, A. D., Djorgovski, S. G., & Yan, L. 2015, ApJ, 815, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Gatti, M., Lamastra, A., Menci, N., Bongiorno, A., & Fiore, F. 2015, A&A, 576, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ge, J.-Q., Hu, C., Wang, J.-M., Bai, J.-M., & Zhang, S. 2012, ApJS, 201, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Gerke, B. F., Newman, J. A., Faber, S. M., et al. 2007, MNRAS, 376, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W. 2001, AJ, 121, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Hernandez, X., Park, C., Cervantes-Sodi, B., & Choi, Y.-Y. 2007, MNRAS, 375, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Ibarra, F. J., Krongold, Y., Dultzin, D., et al. 2016, MNRAS, 459, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Martini, P., et al. 2005, ApJ, 625, L71 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Jiang, C. Y., Jing, Y. P., Faltenbacher, A., Lin, W. P., & Li, C. 2008, ApJ, 675, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., & Lumsden, S. 2001, ApJS, 132, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Khochfar, S., & Burkert, A. 2006, A&A, 445, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kollmeier, J. A., Onken, C. A., Kochanek, C. S., et al. 2006, ApJ, 648, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Koss, M., Mushotzky, R., Treister, E., et al. 2012, ApJ, 746, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Koss, M. J., Blecha, L., Bernhard, P., et al. 2018, Nature, 563, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Lambas, D. G., Tissera, P. B., Alonso, M. S., & Coldwell, G. 2003, MNRAS, 346, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Greene, J. E., Shen, Y., & Strauss, M. A. 2010, ApJ, 715, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Shen, Y., Strauss, M. A., & Hao, L. 2011, ApJ, 737, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, X., Lazio, T. J. W., Shen, Y., & Strauss, M. A. 2018, ApJ, 854, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Lupton, R., Gunn, J. E., Ivezić, Z., Knapp, G. R., & Kent, S. 2001, in Astronomical Data Analysis Software and Systems X, eds. F. R. Harnden, Jr., F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238 [Google Scholar]
- Man, A. W. S., Toft, S., Zirm, A. W., Wuyts, S., & van der Wel, A. 2012, ApJ, 744, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Márquez, I., & Masegosa, J. 2008, in Revista Mexicana de Astronomia y Astrofisica, vol. 27, RM&AC Conf. Ser., 32, 150 [NASA ADS] [Google Scholar]
- McCavana, T., Micic, M., Lewis, G. F., et al. 2012, MNRAS, 424, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Mingarelli, C. M. F., Lazio, T. J. W., Sesana, A., et al. 2017, Nat. Astron., 1, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Moles, M., Marquez, I., & Perez, E. 1995, ApJ, 438, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Comerford, J. M., Nevin, R., et al. 2015, ApJ, 813, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolic, B., Cullen, H., & Alexander, P. 2004, MNRAS, 355, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., & Atfield, J. E. 2008, ApJ, 685, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1969, ApJ, 155, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, M. J., Tissera, P. B., Scannapieco, C., Lambas, D. G., & de Rossi, M. E. 2006, A&A, 459, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Zinchenko, I. A., Cedrés, B., et al. 2012, MNRAS, 419, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Tadhunter, C. N., Inskip, K. J., et al. 2011, MNRAS, 410, 1550 [NASA ADS] [Google Scholar]
- Rosario, D. J., McGurk, R. C., Max, C. E., et al. 2011, ApJ, 739, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Rosas-Guevara, Y., Bower, R., McAlpine, S., Bonoli, S., & Tissera, P. 2019, MNRAS, 483, 2712 [NASA ADS] [CrossRef] [Google Scholar]
- Rubinur, K., Das, M., & Kharb, P. 2018, J. Astrophys. Astron., 39, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Satyapal, S., Ellison, S. L., McAlpine, W., et al. 2014, MNRAS, 441, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Satyapal, S., Secrest, N. J., Ricci, C., et al. 2017, ApJ, 848, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Simmons, B. D., Urry, C. M., Treister, E., & Glikman, E. 2012, MNRAS, 425, L61 [NASA ADS] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Shangguan, J., Liu, X., Ho, L. C., et al. 2016, ApJ, 823, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, L. D., Weller, J., Ostriker, J. P., & Bode, P. 2006, ApJ, 646, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, S., Wadsley, J., & Stinson, G. 2010, MNRAS, 407, 1581 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, X., Greene, J. E., & Strauss, M. A. 2011, ApJ, 735, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Kampczyk, P., Jahnke, K., et al. 2011, ApJ, 743, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. L., Shields, G. A., Bonning, E. W., et al. 2010, ApJ, 716, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Solanes, J. M., Perea, J. D., & Valentí-Rojas, G. 2018, A&A, 614, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinborn, L. K., Dolag, K., Comerford, J. M., et al. 2016, MNRAS, 458, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Teng, S. H., Schawinski, K., Urry, C. M., et al. 2012, ApJ, 753, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Van Wassenhove, S., Volonteri, M., Mayer, L., et al. 2012, ApJ, 748, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Villforth, C., Hamilton, T., Pawlik, M. M., et al. 2017, MNRAS, 466, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Haardt, F., & Madau, P. 2003, ApJ, 582, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Dubois, Y., Pichon, C., & Devriendt, J. 2016, MNRAS, 460, 2979 [Google Scholar]
- Wang, J.-M., Chen, Y.-M., Hu, C., et al. 2009, ApJ, 705, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Weigel, A. K., Schawinski, K., Treister, E., Trakhtenbrot, B., & Sanders, D. B. 2018, MNRAS, 476, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Q., Lu, Y., Mohayaee, R., & Colin, J. 2011, ApJ, 738, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Zhang, X., Dong, X., & Li, C. 2004, ApJ, 604, L33 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Medians (M), lower (Q1), and upper (Q3) quartiles of the DAGN fraction in close pairs predicted by the major merger scenario at z ∼ 0 for bound galaxy pairs with an initial reduced orbital energy rcirc, p of 4/3.
Appendix B: Additional figures
In this Appendix we provide additional figures showing estimates of the incidence of DAGN in major mergers of spiral galaxies included in local surveys of galaxy pairs as a function of the merger timescale, τmer. In these figures, 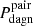 is the fraction of ongoing binary mergers with active BH pairs that can be expected in such datasets (no matter they are observable as spectroscopic duals or not), and
is the fraction of ongoing binary mergers with active BH pairs that can be expected in such datasets (no matter they are observable as spectroscopic duals or not), and 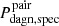 is the expected fraction of these DAGN that simultaneously satisfies the condition for detection by the double peak-method in the optical window. Each group of six panels refers to one of the three representative levels of nuclear activity adopted, which correspond to different thresholds of X-ray bolometric luminosity, from top to bottom: WEAK, INTERMEDIATE, and STRONG. Within these groups of panels, the labels OPEN, WIDE, and CLOSE refer to the criteria used in the definition of the apparent separation of the pairs (see text). As in the Figs. 1–3 of the manuscript, the green dots of the panels show the predictions derived from individual simulations, while the large red circular symbols and associated error bars illustrate the location (median) and scale (interquartile range) of the subset of predictions corresponding to the same initial orbital configuration, i.e. when only the moduli and relative orientation of the internal spins of the merging galaxies are allowed to change, whose values we collect in Table A.1.
is the expected fraction of these DAGN that simultaneously satisfies the condition for detection by the double peak-method in the optical window. Each group of six panels refers to one of the three representative levels of nuclear activity adopted, which correspond to different thresholds of X-ray bolometric luminosity, from top to bottom: WEAK, INTERMEDIATE, and STRONG. Within these groups of panels, the labels OPEN, WIDE, and CLOSE refer to the criteria used in the definition of the apparent separation of the pairs (see text). As in the Figs. 1–3 of the manuscript, the green dots of the panels show the predictions derived from individual simulations, while the large red circular symbols and associated error bars illustrate the location (median) and scale (interquartile range) of the subset of predictions corresponding to the same initial orbital configuration, i.e. when only the moduli and relative orientation of the internal spins of the merging galaxies are allowed to change, whose values we collect in Table A.1.
 |
Fig. B.1. Probabilities |
All Tables
Medians (M), lower (Q1), and upper (Q3) quartiles of the DAGN fraction predicted by the major merger scenario at z ∼ 0.
Medians (M), lower (Q1), and upper (Q3) quartiles of the DAGN fraction in close pairs predicted by the major merger scenario at z ∼ 0 for bound galaxy pairs with an initial reduced orbital energy rcirc, p of 4/3.
All Figures
 |
Fig. 1. Expected incidence of dual active BH in equal-mass mergers of spiral galaxies (of Sb type) in the nearby universe, as a function of the merger timescale, τmer. Pdagn is the intrinsic fraction of binary mergers with active BH pairs and Pdagn, spec is the fraction of these mergers observable through double-peaked narrow line features in the optical window. The panels on each column show results for different representative thresholds of nuclear activity (see text). Top panels: results for a BH lifetime, τagn, of 102 Myr, while bottom panels: results for τagn = 10 Myr. Individual predictions are represented with green dots, while large red open circles and error bars show the median and interquartile range of the subsets of results inferred from the same initial orbital eccentricity, ϵ, which increases from left to right in each panel. This figure is for mergers starting with a reduced orbital energy rcirc, p = 4/3. |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but for Sb+Sc mergers with a mass ratio of 3:1. |
| In the text | |
 |
Fig. 3. Same as Fig. 1 but for equal-mass Sb+Sb mergers with an initial reduced orbital energy rcirc, p = 2.0. |
| In the text | |
 |
Fig. 4. Comparison of our results for Pdagn (top) and Pdagn, spec (bottom) with observations and other theoretical predictions. The total ranges of plausible values for these probabilities inferred from all the major mergers in our suite, i.e. regardless of the orbital eccentricity, orbital energy and mass ratio of the progenitor galaxies, are represented by means of horizontal bands color coded to show the different thresholds of the bolometric X-ray luminosity adopted in our numerical DAGN model (see the inset in the top-left panel). The panels on each column depict results for different durations of the AGN phase, τagn: 100 Myr (left) and 10 Myr (right). Distributed between this figure and Fig. 5, we show a set of benchmarks formed by the individual values and/or ranges of values quoted in the observational works by Rosario et al. (2011, Ros11), Ellison et al. (2011, Ell11), Silverman et al. (2011, Sil11) and Koss et al. (2012, Kos12), which are represented by blue solid circles, those corresponding to our own estimates based on the large AGN surveys by Comerford et al. (2009, Com09) and Ge et al. (2012, Ge12), represented by blue solid squares, as well as those stemming from the cosmological simulations by Rosas-Guevara et al. (2019), Volonteri et al. (2016) and Steinborn et al. (2016) that we group under the same label (Cosmo), and from the isolated merging runs of Capelo et al. (2017, Cap17), which are identified by red solid circles. |
| In the text | |
 |
Fig. 5. Same as Fig. 4 but for the probabilities |
| In the text | |
 |
Fig. B.1. Probabilities |
| In the text | |
 |
Fig. B.2. Same as Fig. B.1 but for an AGN lifetime of 10 Myr. |
| In the text | |
 |
Fig. B.3. Same as Fig. B.1 but for Sb+Sc mergers having a mass ratio of 3:1. |
| In the text | |
 |
Fig. B.4. Same as Fig. B.2 but for Sb+Sc mergers having a mass ratio of 3:1. |
| In the text | |
 |
Fig. B.5. Same as Fig. B.1 but for mergers with rcirc, p = 2.0. |
| In the text | |
 |
Fig. B.6. Same as Fig. B.2 but for mergers with rcirc, p = 2.0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



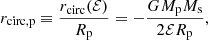
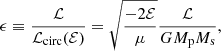
![$$ \begin{aligned} \left[\frac{\tau _{\rm cros}}{\mathrm{Gyr}}\right]\approx 0.006 \left[\frac{{\Delta r}}{\mathrm{kpc}}\right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq3.gif)
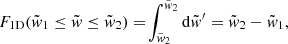
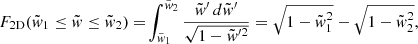
![$$ \begin{aligned} \epsilon _{\rm agn}(i) = \left\{ \begin{array}{ll} 0&\mathrm{if\,\;DAGN\,activity\,is\,not\,feasible,}\\ x \in (0,1]&\mathrm{otherwise,} \end{array} \right. \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq8.gif)
![$$ \begin{aligned} {P_{\rm dagn}}=\frac{1}{\tau _{\rm mer}}\sum _{i=1}^{n}\epsilon _{\rm agn}(i)[t(i+1)-t(i)], \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq9.gif)
![$$ \begin{aligned} {P_{\rm dagn,spec}}=\frac{1}{\tau _{\rm mer}}\sum _{i=1}^{n}p_{\rm obs}(i)\epsilon _{\rm agn}(i)[t(i+1)-t(i)], \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq10.gif)
![$$ \begin{aligned} {P_{\rm dagn}^\mathrm{pair}}=\frac{1}{f_{\rm cat}\tau _{\rm mer}}\sum _{i=1}^{n}p_{\rm cat}(i)\epsilon _{\rm agn}(i)[t(i+1)-t(i)], \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq13.gif)
![$$ \begin{aligned} {P_{\rm dagn,spec}^\mathrm{pair}}=\frac{1}{\tau _{\rm mer}}\sum _{i=1}^{n}p_{\rm catobs}(i)\epsilon _{\rm agn}(i)[t(i+1)-t(i)], \end{aligned} $$](/articles/aa/full_html/2019/04/aa33767-18/aa33767-18-eq14.gif)