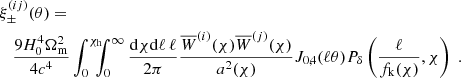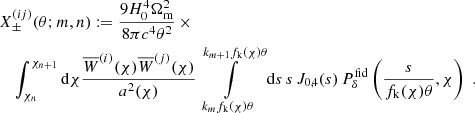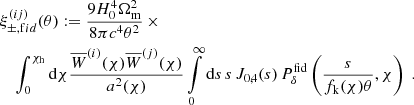| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | C3 | |
| Number of page(s) | 1 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118224e | |
| Published online | 13 April 2022 | |
Retrieving the three-dimensional matter power spectrum and galaxy biasing parameters from lensing tomography (Corrigendum)
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: psimon@astro.uni-bonn.de
Key words: methods: data analysis / large-scale structure of Universe / dark matter / errata, addenda
We report a missing factor, a(χ), in the ξ±-related integrands of the original paper. This typographical error in Eqs. (11), (16), and (17) has no impact on our results and conclusions; the correct integrands were used in the original analysis.
A detailed list of the three typographical errors follows. First, the integral for the shear-shear correlations in Eq. (11) should have the factor a2(χ) in the denominator of the integrand (instead of just a(χ)),
Second, the integral for the basis functions in Eq. (16) should also have the factor a2(χ),
Third, the integral in Eq. (17) must have the factor a2(χ),
All three of the correct equations shown here were used in our original analysis. Therefore, the corrections have no impact on our results and conclusions of the original paper.
© ESO 2022
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.