| Issue |
A&A
Volume 645, January 2021
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 11 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201937149 | |
| Published online | 21 December 2020 | |
Fast and accurate approximation of the angle-averaged redistribution function for polarized radiation
1
School of Mathematics and Actuarial Science, University of Leicester, LE1 7RH Leicester, UK
2
Department of Mathematics, Shiraz University of Technology, Modarres BLVD, Shiraz 71555-313, Iran
3
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), PO Box: 19395-5746, Tehran, Iran
4
Istituto Ricerche Solari Locarno, 6605 Locarno-Monti, Switzerland
e-mail: ernest@irsol.ch
5
Leibniz-Institut für Sonnenphysik (KIS), 79104 Freiburg, Germany
Received:
20
November
2019
Accepted:
20
September
2020
Context. Modeling spectral line profiles taking frequency redistribution effects into account is a notoriously challenging problem from the computational point of view, especially when polarization phenomena (atomic polarization and polarized radiation) are taken into account. Frequency redistribution effects are conveniently described through the redistribution function formalism, and the angle-averaged approximation is often introduced to simplify the problem. Even in this case, the evaluation of the emission coefficient for polarized radiation remains computationally costly, especially when magnetic fields are present or complex atomic models are considered.
Aims. We aim to develop an efficient algorithm to numerically evaluate the angle-averaged redistribution function for polarized radiation.
Methods. The proposed approach is based on a low-rank approximation via trivariate polynomials whose univariate components are represented in the Chebyshev basis.
Results. The resulting algorithm is significantly faster than standard quadrature-based schemes for any target accuracy in the range [10−6, 10−2].
Key words: line: formation / line: profiles / methods: numerical / polarization / radiative transfer / scattering
© ESO 2020
1. Introduction
Synthesizing spectral line profiles through radiative transfer (RT) calculations, out of local thermodynamic equilibrium conditions, is a key problem in current solar and stellar physics research. In solar physics, particular attention is nowadays paid to the RT modeling of the polarization profiles of strong resonance lines because they encode valuable information on the magnetic properties of two atmospheric layers of high scientific interest, namely the chromosphere and transition region. Unfortunately, the well-known Zeeman effect turns out to be of limited utility for investigating the weak and tangled magnetic fields that are generally present in these hot regions, and alternative diagnostic methods are therefore being developed. Chief among them are those that exploit the combined action of scattering polarization (i.e., polarization produced by the scattering of anisotropic radiation), along with its modification due to the presence of a magnetic field (Hanle effect), and the Zeeman effect (Trujillo Bueno 2014). The information on the magnetism of the upper chromosphere that was made available from the data acquired through the recent Chromospheric Lyman-Alpha SpectroPolarimeter (CLASP) experiment is just one example of the success of such approaches (Kano et al. 2017; Trujillo Bueno et al. 2018).
A major difficulty in modeling strong resonance lines is the need to account for frequency correlations between incoming and outgoing photons in scattering processes. Taking partial frequency redistribution (PRD) effects into account is necessary in order to correctly model the wings of the intensity profiles in strong spectral lines, and is crucial for reproducing the large scattering polarization signals that are observed in the wings of such lines. Modeling PRD effects is notoriously difficult, especially from the computational point of view, representing a true challenge (both theoretically and numerically) when scattering polarization and the Hanle and Zeeman effects are taken into account.
In this work we present a new method to quickly compute the emission coefficient for polarized radiation, accounting for PRD effects through the redistribution matrix formalism, under the simplifying assumption of angle-averaging. This article is organized as follows. In Sect. 2 we formulate the problem, introducing the relevant quantities. In Sects. 3 and 4, we describe and validate the new approximation algorithm. In Sect. 5 we test its performance in a physically relevant application. Conclusions and perspectives are presented in Sect. 6.
2. Formulation of the problem
A convenient way to describe PRD phenomena is through the redistribution function formalism. This formalism was initially developed for the unpolarized case (e.g., Hummer 1962) and was subsequently generalized to the case in which polarization phenomena are taken into account.
2.1. The unpolarized case
Neglecting polarization effects, the scattering contribution to the line emission coefficient, at reduced frequency u and for direction Ω, is given by
where R(u′, Ω′, u, Ω) is the redistribution function, I((u′, Ω′) is the intensity of the incoming radiation, and kL is the frequency-integrated absorption coefficient. Hereafter, we follow the convention according to which the primed quantities refer to the incident radiation and the unprimed ones to the scattered radiation.
Throughout this work, we focus only on the redistribution function characterizing scattering processes that are coherent (in frequency) in the atomic rest frame. Following the terminology introduced by Hummer (1962), this redistribution function is referred to as RII. In the atomic reference frame, its frequency and angular dependencies are completely decoupled, but in the observer’s frame the Doppler effect introduces a complex coupling of frequencies and angles, making the evaluation of RII and of the integrals of Eq. (1) very demanding from the computational point of view.
The angle-averaged approximation. In order to make the problem computationally simpler, Rees & Saliba (1982) proposed the so-called angle-averaged approximation, which allows decoupling the frequency and angular dependencies also in the observer’s frame. Under this assumption, RII can be written as
The quantity 𝒫 is the so-called angular/angle phase function, whose explicit expression is not relevant for the following discussion. The explicit form of the frequency-dependent part, for the simplest case of a two-level atom with an infinitely sharp lower level, is
where ΓR, ΓI, and ΓE are the line broadening constants due to radiative decays, inelastic de-exciting collisions, and elastic collisions, respectively (these quantities only depend on the spatial point), Θ is the angle between the incoming and scattered direction (scattering angle), H is the Voigt function, and a is the damping constant, which depends only on the spatial point.
As will be explained in further detail below, the angle-averaged approximation introduces considerable inaccuracies in the calculations of the emission coefficient. Thanks to increases in computational power over the last decades, this approximation has been progressively abandoned in favor of angle dependent PRD calculations, which allow for more reliable quantitative comparisons between synthetic and observed intensity profiles.
2.2. The polarized case
We now consider the polarized case, accounting for scattering polarization and the Hanle and Zeeman effects. We still refer to the simple case of a two-level atom, here also in the presence of a magnetic field. However, the following discussion also holds for more complex atomic models, such as multilevel atoms, multiterm atoms, or atoms with hyperfine structure. The polarization properties of the radiation field are commonly described through the four Stokes parameters, I, Q, U, and V (where I is the specific intensity). In analogy with Eq. (1), the emission coefficient in the four Stokes parameters is given by
where the indices i and j can take values 0, 1, 2, and 3, standing for Stokes I, Q, U, and V, respectively, and [R]ij is a 4 × 4 matrix that generalizes the concept of redistribution functions to the polarized case.
Again, we focus on the redistribution matrix characterizing scattering processes that are coherent in the reference frame of the atom, [RII]ij, accounting for Doppler redistribution in the reference frame of the observer. Its expression is significantly more complex than in the unpolarized case because, in order to model scattering polarization, it is necessary to provide a complete description of the atomic system, specifying the population of each magnetic sublevel as well as the coherence that may be present between pairs of sublevels. The inclusion of the latter physical ingredient is responsible for the appearance in the redistribution matrix of additional terms that, instead of the Voigt profile H, involve the associated dispersion profile L (e.g., Landi Degl’Innocenti & Landolfi 2004). Moreover, when a magnetic field is present, the redistribution matrix is given by a linear combination of various terms, each being associated to a particular scattering channel |ℓ⟩ → |u⟩→|ℓ′⟩, where |ℓ⟩ and |ℓ′⟩ indicate the initial and final lower magnetic sublevels involved in the scattering process, and |u⟩ the intermediate upper magnetic sublevel. The various terms are shifted in frequency with respect to each other due to the energy shifts induced in the presence of a magnetic field1.
2.2.1. The angle-averaged approximation
Even with the computational resources that are nowadays commonly available, dealing with the general, angle-dependent expression of [RII]ij is a formidable task. For this reason, it is customary to introduce, in full analogy with the unpolarized case, the angle-averaged assumption. As shown in detail in Appendix A for the case of a two-level atom in the presence of a magnetic field, the frequency-dependent part of [RII − AA]ij is given by a linear combination of functions of the form
where we have introduced the angle γ = Θ/2, and where H and L are the Voigt and the associated dispersion profiles, respectively. The arguments x and y, which take into account the magnetic splitting of the Zeeman sublevels, are given by
where Δℓℓ′ is the frequency splitting (in Doppler width units) between lower sublevels ℓ and ℓ′ and Δuℓ is the frequency shift (in Doppler width units) of the Zeeman transition between sublevels u and ℓ with respect to the line-center frequency. We note that, when Δuℓ and Δℓℓ′ are zero, the function f is equivalent to the integral appearing in Eq. (3), inclusive of the 1/(2π) factor.
Like in the unpolarized case, the angle-averaged assumption represents a strong approximation, as it smoothens geometrical aspects of the problem that may have a significant impact on polarization. Nonetheless, there is still high interest in modeling scattering polarization under this approximation. The main reason is that the computational cost for carrying out detailed angle-dependent calculations in the presence of polarization phenomena is still prohibitive except when taking the simplest modeling of the solar atmosphere (see Sampoorna et al. 2019) or when introducing other simplifying assumptions such as cylindrical symmetry (see del Pino Alemán et al. 2020). It is also for this reason that, to date, few quantitative analyses of the impact of the angle-averaged assumption on the modeling of scattering polarization have been carried out. Theoretical investigations performed in isothermal atmospheric models (see Sampoorna et al. 2017; Nagendra & Sampoorna 2011) have shown that this approximation can give rise to significant inaccuracies, although mainly in the core of the scattering polarization signals.
Nevertheless, under the angle-averaged approximation it is still possible to conduct investigations of scientific interest, especially regarding the modeling of the large polarization signals produced by coherent scattering processes in the wings of strong resonance lines. Although approximate, an angle-averaged PRD approach contains the relevant physics (coherent scattering), and allows modeling such signals, which would be lost under a complete frequency redistribution (CRD) approach. For instance, by making an angle-averaged PRD modeling of the H I Lyman-α line, Belluzzi et al. (2012) predicted that linear polarization signals of large amplitude should be found in the wings of this line. This theoretical result was subsequently confirmed by the observations carried out by the CLASP sounding rocket experiment (Kano et al. 2017). Moreover, the recent discovery that the wing scattering polarization signals in a variety of spectral lines are sensitive to magnetic fields through magneto-optical effects (del Pino Alemán et al. 2016; Alsina Ballester et al. 2016, 2018, 2019) has further awakened the interest in modeling their polarization profiles taking PRD effects into account, also in scenarios that can only be feasibly considered by making the angle-averaged approximation.
We finally observe that, at present, PRD scattering polarization calculations can only be performed in one-dimensional (1D) models of the solar atmosphere. The angle-averaged approximation would not be justified in 3D because it would cancel out important geometrical effects, thus negating the effort of making a full 3D modeling. On the other hand, when accepting the simplifications of a 1D modeling this approximation still represents a good compromise between accounting for the relevant physics of the problem and reducing the computational requirements of a PRD calculation.
2.2.2. The computational challenge
Even under the angle-averaged assumption, calculating the emission coefficient in the four Stokes parameters at a given spatial point, frequency, and direction is a computationally demanding task that requires many evaluations of the redistribution matrix [RII − AA]ij. As noted above, it is generally composed of many different terms containing the functions f and h for shifted values of x and y. As an example, in order to model the Na I doublet at 589 nm, a two-term atom with hyperfine structure must be considered. The redistribution matrix for this atomic model, in the presence of magnetic fields, contains on the order of 100 distinct terms. Moreover, at each iterative step of the numerical solution of a standard RT problem, the emission coefficient must be evaluated a considerable amount of times: at every spatial point in the considered model atmosphere and at all frequencies and propagation directions of the chosen frequency and angular grids of the problem2. This clearly highlights the importance of developing faster methods for calculating [RII − AA]ij and the integrals appearing in Eq. (4), without compromising the accuracy of the calculations beyond the level that can be achieved under the angle-averaged approximation.
A direct approximation of the functions f and h using quadrature rules is challenging because the integrands depend strongly on the values of x and y. In particular, the integrands exhibit a steep decay to zero both for γ → 0 when 0 < |x|≪1, and for γ → π/2 when |y|≪1. Therefore, an accurate approximation of these functions may require numerous quadrature points. Devising a strategy that, for each pair (x, y), selects a quadrature rule by balancing accuracy and computational cost is technical and tedious, and may need case-by-case adjustments.
To tackle this issue, approximations to quickly evaluate the function f have been proposed in the past (e.g., Adams et al. 1971; Gouttebroze 1986; Uitenbroek 1989). Unfortunately, these techniques cannot be directly extended to the function h. In this work, we propose a new method to approximate the functions appearing in Eqs. (5) and (6), which allows for a substantial speed-up with respect to quadrature-based approaches while keeping the error well below those originating from other approximations introduced in the problem (e.g., the angle-averaged assumption).
3. Fast and accurate approximation of f
In this work we present a novel approach that involves replacing the aforementioned functions f and h, which have dependencies on u, u′, and a, by low-rank approximations in terms of a trivariate polynomial. Its univariate components are represented in the Chebyshev basis. Such polynomials can be constructed and stored easily using the MATLAB-software package Chebfun. The MATLAB-code used in the following sections is available at Paganini & Hashemi (2020). Using MATLAB’s product Coder3, the resulting approximations can be exported as C or C++ code to be used in existing software for RT calculations. In the following section we focus our attention on the function f.
3.1. Restriction to a bounded domain
The first step in constructing an approximation of f is to identify the domain where the approximation needs to be accurate. Firstly, we observe that the integrand in Eq. (5) is an even function with respect to both x and y. Therefore, we can restrict our considerations to the positive quadrant x, y ≥ 0.
Secondly, f(x, y, a) exhibits a super-exponential decay in the variable x and is smaller than 10−16 for x > 6 (see Fig. 1). Therefore, we can restrict our considerations to the interval x ∈ [0, 6].
 |
Fig. 1. Plot of log10f(x, y, a) for a = 10−3 and x, y ∈ [0, 10]. The two bold lines indicate the f = 10−10 and the f = 10−20 contours. Image values smaller than 10−30 are not plotted. We observe a rapid decay in the x direction. The qualitative behavior of log10f is similar for a ∈ [10−5, 10−1]. |
Finally, we do not observe any particularly notable behavior in the dependence on y or a. We decide to consider the interval y ∈ [0, 10] and a ∈ [10−5, 10−1] because these are the regimes that are typically considered in most applications. We note that considering a larger interval for y or a presents no particular difficulty beyond a modest increase in computational cost.
3.2. Interpolation with Chebfun
Having identified the interpolation domain [0, 6]×[0, 10]×[10−5, 10−1], we can proceed to the construction of a trivariate polynomial for approximating the function given by Eq. (5). Since f exhibits a fast decay (but remains positive), it is convenient to interpolate log f instead to better control the relative error. Additionally, to have equidimensional ratios of the interpolation domain, we replace the variable a with its base-10 logarithm b. Therefore, we want to construct a trivariate polynomial p such that
where log f denotes the natural logarithm of f.
Constructing a trivariate interpolant that is highly accurate is notoriously difficult. In this work, we use Chebfun3 (Hashemi & Trefethen 2017), a component of the MATLAB-software package Chebfun (Driscoll et al. 2014). All Chebfun3 needs to construct the interpolant p is a MATLAB-function that, for a triplet (x, y, b), returns the value log f(x, y, 10b). The details of computing log f are discussed in Sect. 3.3. Then, the interpolant p can be computed with the following code
BD = [0,6,0,10,-5,-1]; p = Chebfun3(logf, BD, ''eps'', 1e-11);
The first line of this code specifies the interpolation domain boundary, whereas the second line constructs the interpolant p. The option “eps” specifies the desired target accuracy. It is important to stress that setting “eps” to 10−11 does not guarantee that p has 10 digits of accuracy. Computing errors of trivariate interpolants is computationally expensive (as it requires evaluating p over the whole interpolation domain). Therefore, the software Chebfun3 uses some heuristics to determine the accuracy of p.
The function p returned by Chebfun3 represents a trivariate polynomial in the following continuous analog of the Tucker decomposition of discrete tensors (Golub & Van Loan 2013, Sect. 12.5)
where CT ∈ ℝr1 × r2 × r3 is the so-called core tensor, and ci(x), si(y), and tk(b) are univariate polynomials.
To construct (10), Chebfun3 exploits low-rank compression of f via multivariate adaptive cross approximation, which is an iterative application of a multivariate extension of Gaussian elimination with complete pivoting. The trilinear rank (r1, r2, r3) as well as the degree of each set of polynomials ci, sj, tk are all chosen adaptively by the algorithm. We refer to Hashemi & Trefethen (2017) for more details.
3.3. Accurate evaluation of f via integration
To construct the interpolant p, we need an algorithm that evaluates the function log f, and thus f, to high accuracy. This can be done using a Gauss quadrature formula.
At this stage, it is not strictly necessary to evaluate f quickly because the time invested in computing f does not affect the speed of the subsequent evaluation of p. However, computational efficiency is always appreciated. Therefore, we want to select an appropriate number of quadrature points to speed up computations. For this goal, it is instructive to plot the integrand of Eq. (5) for some chosen values of x, y, and a. In Fig. 2 we observe that, as x increases, the upper left corner smoothens. Similarly, the upper right corner smoothens as y increases. When y is small, the variable a also affects the curvature of the upper right corner. For other values of y the qualitative impact of a is negligible (not shown).
From these observations we can speculate that approximating f becomes particularly challenging when x or y are close to zero. This is confirmed in a numerical experiment, where we compare the difference between the value of f approximated with nQ and nQ+50 Gauss quadrature points (with nQ = 50, 10, …, 3000). The results are plotted in Fig. 3. The most challenging integral arises with a = 10−5 and x = y = 0. In this case, it takes more than 2500 Gauss quadrature points to approximate f to machine precision. The number of quadrature points necessary to achieve machine precision decreases drastically if x, y, or a increase.
 |
Fig. 3. Gauss quadrature error in approximating f. The number of quadrature points necessary to achieve machine precision depends on the values of x, y, and a. |
After extensive numerical investigations, we decided to employ the following strategy to efficiently and accurately approximate f. If x ≥ 0.05 and y ≥ 0.05, we use 250 Gauss quadrature points. Otherwise, we use 700 Gauss quadrature points if a ≥ 10−4 and 2500 Gauss quadrature points if a < 10−4.
3.4. Results
At this point, we can finally construct the trivariate polynomial p. In this example, we set the parameter “eps” to 10−11.
After a roughly 140-minute-long computation on a standard laptop, mostly due to evaluating f on interpolation points, Chebfun returns the interpolant p given in Eq. (9). In reference to Eq. (10), its core CT is a 40 × 74 × 24 tensor, and the ci, sj, and tk are univariate polynomials of degree 66, 257, and 32, respectively. We can gather some extra information by plotting the Chebyshev coefficients of these polynomials (using the Chebfun command plotcoeffs). The result is displayed in Fig. 4. We observe that the coefficients of ci and tk decay exponentially, whereas the coefficients of (some of the) sj reach a plateau. This indicates that the difficulty in approximating f is mostly due to a nonanalytic behavior of f in the y direction.
To assess the accuracy of the constructed Chebfun3-based approximation, we consider the set of values of b = −5, −5 + 1/20, …, −1 and sample the error
on the (x, y)-grid
In Fig. 5 we plot the statistics of these sampled errors. The 1-quantile corresponds to the maximum error. We observe that, in the worst case scenario, the Chebfun-based approximation has 5 digits of accuracy, and that for a > 10−3 the number of exact digits is 6. However, we also observe that the error is less than 10−8 for 95% of the points in G.
In certain physical situations it is advantageous to solve the RT equation in optical depth scale instead of geometric depth scale (e.g., Janett et al. 2017; Janett & Paganini 2018). After performing the required change of variables, the key physical quantity for the solution of the RT equation is no longer the emission coefficient, but rather the so-called source function (i.e., the ratio between the emission and absorption coefficients).
This calls for the calculation of the following function
where the absorption profile ϕ is given by
It is thus also interesting to investigate the accuracy of the proposed approximation for g(x, y, a). For the sampling values of x, y, and a used in this section, ϕ(u) ∈ [10−8, 10−3]. Therefore, one could wonder whether the function ϕ(u) could nullify our efforts to approximate [RII − AA]ij(u′,u) accurately. Luckily, this turns out not to be the case, as we can observe in Fig. 6, where we plot the values of
We therefore conclude that the approximation presented here is extremely accurate even after dividing by ϕ(u).
3.5. Evaluation of the polynomial approximation
It is important to realize that, although it may take some time to construct a Chebfun3 object, the subsequent evaluation of p is very fast. To evaluate it at a point 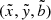 it is necessary to first compute the values of the univariate polynomials ci, sj, and tk in
it is necessary to first compute the values of the univariate polynomials ci, sj, and tk in 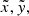 and
and 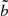 , respectively. This can be done using 1D Clenshaw recurrence (Clenshaw 1955; Driscoll et al. 2014), which is numerically stable and fast; its time complexity is linear in terms of the degree of the polynomials. Then, the values
, respectively. This can be done using 1D Clenshaw recurrence (Clenshaw 1955; Driscoll et al. 2014), which is numerically stable and fast; its time complexity is linear in terms of the degree of the polynomials. Then, the values 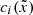 ,
, 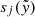 ,
, 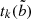 are organized in vectors
are organized in vectors 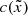 ,
, 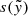 , and
, and 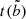 . Finally, the value
. Finally, the value 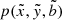 is obtained by computing the modal products (Golub & Van Loan 2013, p. 727) of the core tensor CT with
is obtained by computing the modal products (Golub & Van Loan 2013, p. 727) of the core tensor CT with 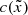 ,
, 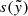 , and
, and 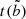 . These operations are also fast because, internally, they call high-performance implementations of Basic Linear Algebra Subroutines (BLAS) tuned by computer vendors for maximal speed and efficiency.
. These operations are also fast because, internally, they call high-performance implementations of Basic Linear Algebra Subroutines (BLAS) tuned by computer vendors for maximal speed and efficiency.
To make an illustrative example, we fixed the value of b and evaluated p(x, y, b) at 105 random points (x, y) ∈ [0, 5]×[0, 5]. Such an experiment took roughly 12 seconds. The evaluation is dramatically faster if the points (x, y) lie on a regular grid. In this case, one can exploit the special structure of the regular grid, and evaluating p on 106 points takes only a fraction of a second. However, in the applications considered in this work, it is very rarely the case that one evaluates (5) on a regular grid. Therefore, the previous experiment with random points is more enlightening.
Remark 1. In practice, the emission coefficient must be evaluated through Eq. (4) at each individual spatial point. This requires the evaluation of p(x, y, b) for many values of x and y, but with b fixed. In this case, it is convenient to extract a Chebfun2 object from p, that is, its equivalent bivariate counterpart obtained by fixing the value of b. This Chebfun2 object can be computed with the simple Chebfun-command p2 = p(:,:,b). The resulting bivariate polynomial p2 returns exactly the same values of p, that is, p2(x, y) = p(x, y, b), but it is much faster (because it does not need to re-evaluate the polynomials tk in Eq. (10)). For instance, evaluating p2 at 105 random points (x, y) ∈ [0, 5]×[0, 5] takes only roughly 4 s.
4. Fast and accurate approximation of h
In this section we discuss how to approximate the function introduced in Eq. (6), in close analogy to the previous section. We first point out that the integrand contains the associated dispersion profile, which is an odd function in its second argument. For this reason, we can likewise restrict our considerations to the positive quadrant x, y ≥ 0. Because the function h also exhibits a super-exponential decay in the variable x, we can restrict our considerations to the interval x ∈ [0, 6]. Finally, the main difference between (6) and (5) is that the associated dispersion function vanishes when its second argument is zero, that is, L(⋅, 0) = 0. In light of these considerations, we compute two different approximations of (6): one for y ∈ [10−13, 10−1] and one for y ∈ [10−1, 10].
For the regime y ∈ [10−1, 10] we employ the same strategy used in Sect. 3, and construct a trivariate polynomial q such that
On the other hand, for the regime y ∈ [10−13, 10−1] it is more convenient to construct a trivariate polynomial 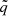 such that
such that
Finally, in the regime y ∈ [0, 10−13], the function h satisfies h < 4.1 × 10−13, and it can be simply approximated by the zero-constant function.
Similarly to Sect. 3, the approximants (16) and (17) can be computed using Chebfun. The approximant q is a trivariate polynomial in the Tucker form whose core tensor is of size 18 × 33 × 11 with polynomials ci, sj, and tk of degree 28, 127, and 40, respectively. Also, the approximant 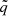 has trilinear rank (6, 21, 17) with polynomials ci, sj, and tk of degree 30, 257, and 41, respectively. In Figs. 7 and 8 we display the quantiles of the error described in Sect. 3.4 (without dividing by ϕ(u)). These figures show that the constructed approximation is extremely accurate.
has trilinear rank (6, 21, 17) with polynomials ci, sj, and tk of degree 30, 257, and 41, respectively. In Figs. 7 and 8 we display the quantiles of the error described in Sect. 3.4 (without dividing by ϕ(u)). These figures show that the constructed approximation is extremely accurate.
5. Comparison on a physical application
To make a comparison of practical interest, we consider the evaluation of the integral over u′ contained in Eq. (1). This corresponds to the unpolarized case, in which only the function f appears in the problem. The extension to the polarized case, in which both functions f and h are involved (see Sect. 2 and Appendix B), is discussed at the end of this section.
In this experiment, we assume 𝒫(Ω′, Ω) = 1 in Eq. (2) (isotropic scattering), and we introduce the mean intensity
For simplicity, we consider a single spatial grid point in the atmospheric model. Let {ui}, i = 1, …, NF, be the grid of reduced frequencies at that point4. Our goal is to calculate, at all the emitted reduced frequencies {ui}, the integral (often referred to as scattering integral)
which is related to the emission coefficient simply as
Since f presents sharp variations with u′, approximating integral (19) with the trapezium rule on the grid {ui} does not return accurate results. A successful approach, in this case, is to construct an interpolant of J and then perform the integration on a much finer grid.
Following this approach, let {bj(u′)} be an interpolation basis such that bj(ui) = δij. Then, the interpolant of J can be written as
where μj denote the interpolant coefficients (μj = J(uj)). After this substitution, the scattering integral (19) can be approximated by
where the quadrature weights are given by
From Eq. (22) we conclude that the main computational cost is approximating the quadrature weights Fji. Indeed, once these have been found, integral (19) can be computed almost instantaneously with formula (22).
Of course, the quadrature weights Fji depend on the basis functions {bj(u′)} used in Eq. (21). In the past, different authors have recommended using cardinal natural interpolatory cubic splines (e.g., Adams et al. 1971; Gouttebroze 1986; Uitenbroek 1989). The order of convergence of cubic splines is quartic, but their interpolatory basis functions are oscillatory and have global support. This introduces an extra difficulty in evaluating the weights Fji. Developing an efficient algorithm to compute these weights is beyond the scope of this work, and we postpone it to future research. In this work, we consider linear B-splines instead. Linear B-splines are piecewise linear functions and have compact support, which simplifies the task of computing Fji.
Assuming that the values {ui} increase monotonically, the linear B-spline associated with an internal frequency point uj ∈ (u1, uNF) is
There is some freedom in defining the linear B-splines associated with the first and the last frequency points. Given that in the applications considered below we will only consider basis functions associated with internal points, this choice is not particularly relevant for the scope of this work. However, one can, for instance, consider extension by a constant value, and use
and
respectively.
In principle, the interval of integral (23) is the whole real line. However, since bj has compact support, we can restrict the integration interval to (uj − 1, uj + 1). Moreover, the function f decays super-exponentially as the quantity |u′−ui| increases (see Fig. 1). Therefore, it is necessary to integrate (23) only for u′ in
An efficient way to compute integral (23) is to further split interval (24) at ui and uj and use different Gauss quadrature rules in each subinterval because bj and f are not smooth functions. Without going into details, for each non-empty interval given by Eq. (24), this approach is expected to require at least (roughly) 20 quadrature points in total.
In this numerical experiment, we evaluate f on these quadrature points using Chebfun-based approximations. The goal is to make a comparison in terms of speed and accuracy with direct computations of Eq. (5) based on quadrature rules.
To give this experiment a realistic application flavor, we use a grid of reduced frequencies considered in a realistic RT problem. In particular, our grid is the one used in the RT investigation of the Mg IIk line presented in Alsina Ballester et al. (2016), specifically corresponding to the height point at 2075 km in the atmospheric model C of Fontenla et al. (1993). This reduced frequency grid consists of 109 points spanning the range between u = −333.5 and u = 328. It contains 23 equispaced points in the core of the line, with the remaining points being logarithmically spaced outside this range.
For this grid, we consider every nonempty interval of the form (24) (which in this case are 4005), and for each of these we collect 10, 20, and 40 quadrature points (for a total of 40 050, 80 100, and 160 200). Using 10 points corresponds to a coarse approximation of (23), whereas between 20 and 40 Gauss quadrature points should be considered for higher accuracies. To simplify the numerical experiment, we replace composite Gauss quadratures with the trapezium rule.
For each of these four cases, we measure the time necessary to evaluate (5) at all quadrature points using Chebfun-based approximations with parameter eps = 10−5, 10−6, 10−7, 10−8, 10−9, 10−10, 10−11, and using a direct Gauss-quadrature approximation5 with 8, 16, 32, 64, 128, 256, 512 points. For Chebfun-based solutions, we consider both approximations obtained by evaluating the Chebfun3 object (10) as well as approximations obtained by evaluating a Chebfun2 object generated by fixing b = log10a in the original Chebfun3 object. These two Chebfun-based approximations return exactly the same values, but have different execution times, because the original Chebfun3 object inevitably re-evaluates the polynomials tk (see Eq. (10)). We also compute the maximum error for each of these approximations using self- and cross-comparison. Self-comparison means that we consider convergence of Chebfun-based solutions to the values obtained using the Chebfun-based solutions with eps = 10−11, and the convergence of quadrature-solutions to the quadrature-solution with 512 Gauss quadrature points. Cross-comparison means that we consider convergence of Chebfun-based solutions to the quadrature-based solution with 512 Gauss quadrature points, and convergence of quadrature-based solutions to the Chebfun-based solutions with eps = 10−11.
In Figs. 9 and 10, we display the error versus computational time for Chebfun-based and quadrature-based solutions. In these simulations, the error ranges within the interval [10−6, 10−2], which is the most relevant for practical applications. We observe that the Chebfun2-based solutions are notably faster than quadrature-based solutions. For instance, the slowest (and most accurate) Chebfun2-based object requires essentially the same computational time as the quadrature-based solution obtained with 32 Gauss quadrature points (and it is 3 orders of magnitude more accurate). We also note that the Chebfun3-based approximations are as fast as quadrature-based solutions for errors smaller than 2 × 10−4, if not faster. Finally, we observe that, in the cross-comparison plot, Chebfun- and quadrature-based solutions converge to each other until the error is below 10−6, at which point the “convergence lines” plateau. This is expected because Chebfun solutions can guarantee a precision of roughly 10−7 (cf. Fig. 5).
 |
Fig. 9. Self-comparison error versus computational time of Chebfun-based and quadrature-based approximations of f on 4005 × 10, 20, 40 quadrature points. The circles on the curves for quadrature-based solutions indicate, for decreasing error, the results obtained taking 8, 16, 32, 64, 128, and 256 quadrature points. The circles on the curves for Chebfun solutions indicate, for decreasing error, the results obtained taking eps = 10−5, 10−6, 10−7, 10−8, 10−9, and 10−10. |
 |
Fig. 10. Cross-comparison error versus computational time of Chebfun-based and quadrature-based approximations of f on 4005 × 10, 20, 40 quadrature points. The circles on the curves for quadrature-based solutions indicate, for decreasing error, the results obtained taking 8, 16, 32, 64, 128, 256, and 512 quadrature points. The circles on the curves for Chebfun solutions indicate, for decreasing error, the results obtained taking eps = 10−5, 10−6, 10−7, 10−8, 10−9, 10−10, and 10−11. |
Remark 2. In this numerical experiment, we have analyzed the time required to compute the emission coefficient at a single spatial point and in the absence of polarization. We now comment on these two simplifications.
As mentioned previously, standard 1D semi-empirical models of the solar atmosphere easily contain 100 spatial points or more. Since the values of the reduced frequencies and of the damping parameter vary with the spatial point, a simulation with 100 spatial points requires computing 100 different sets of quadrature weights {Fji} (23), and thus the gain in computational time is multiplied by 100 if these are not computed in parallel.
The computation of the emission coefficient for polarized radiation is fully analogous to the unpolarized case. Deferring the details to Appendix B, we mention that the polarized case additionally requires the computation of quadrature weights of the form (23) replacing the function f by the function h. Repeating the previous experiments for function h would simply produce plots similar to Figs. 9 and 10 because the approximation of h is completely analogous to the approximation of f. On top of that, in the presence of a magnetic field – or when considering an atomic model more complex than one with two levels – multiple sets of functions f and h with different shifts in their arguments are involved and a separate quadrature weight must be determined for each of them (see Eqs. (B.9) and (B.10)). Clearly, the overall computation time scales with the number of quadrature weights that are required.
6. Conclusion
We have presented a new method for approximating the functions f and h that appear in the angle-averaged redistribution matrix for polarized radiation [RII − AA]ij. The new method uses low-rank approximation and Chebyshev polynomials to construct functions that approximate f and h. These approximating functions can be evaluated quickly using Clenshaw recurrence. The level of accuracy does not deteriorate when dividing these approximating functions by the absorption profile to compute the source function. Numerical experiments performed in a realistic scenario show that our approach permits significantly faster computations than standard algorithms based on quadrature rules, while achieving similar or higher accuracies. In addition, at any given height point (where the parameter a is fixed), the evaluation can be carried out even faster using Chebfun2 objects generated as cross-sections of the main Chebfun3 object.
The decrease in computational cost provided by this new method will be very useful for RT investigations of scattering polarization and the Hanle and Zeeman effects in strong resonance lines, accounting for the impact of PRD phenomena, either in physical situations for which an angle-dependent treatment is not presently feasible, or when rapid calculations at a low computational cost are required. This method is expected to be particularly valuable when considering complex atomic models such as multi-term atoms or atoms with hyperfine structure.
When a multilevel atom, a multiterm atom, or an atom with hyperfine structure is considered, the lower sublevels |ℓ⟩ and |ℓ′⟩ can pertain to different fine structure or hyperfine structure levels (Raman scattering). In this case, the redistribution matrix is given by a linear combination of various terms also in the absence of magnetic fields.
Typical frequency and angular grids contain roughly 100 frequency points and 100 directions, respectively. Standard 1D semi-empirical models of the solar atmosphere contain roughly 100 spatial points (heights), while three-dimensional (3D) models obtained from MHD simulations may easily contain 5003 = 1.25 × 108 points.
More information about MATLAB Coder is available on MATLAB’s website https://www.mathworks.com/.
Acknowledgments
The work of B.H. was in part supported by a grant from IPM (No. 99650033). E.A.B. and L.B. gratefully acknowledge financial support from the Swiss National Science Foundation (SNSF) through Grants No. 200021_175997 and CRSII5_180238.
References
- Adams, T. F., Hummer, D. G., & Rybicki, G. B. 1971, J. Quant. Spectr. Rad. Transf., 11, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2016, ApJ, 831, L15 [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2017, ApJ, 836, 6 [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2018, ApJ, 854, 150 [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo Bueno, J. 2019, ApJ, 880, 85 [Google Scholar]
- Belluzzi, L., Trujillo Bueno, J., & Štěpán, J. 2012, ApJ, 755, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Bommier, V. 1997, A&A, 328, 706 [NASA ADS] [Google Scholar]
- Clenshaw, C. W. 1955, Math. Comput., 9, 118 [CrossRef] [Google Scholar]
- del Pino Alemán, T., Casini, R., & Manso Sainz, R. 2016, ApJ, 830, L24 [Google Scholar]
- del Pino Alemán, T., Trujillo Bueno, J., Casini, R., & Manso Sainz, R. 2020, ApJ, 891, 91 [CrossRef] [Google Scholar]
- Driscoll, T. A., Hale, N., & Trefethen, L. N. 2014, Chebfun Guide (Oxford: Pafnuty Publications) [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [Google Scholar]
- Golub, G. H., & Van Loan, C. F. 2013, Matrix Computations, 4th edn. (Johns Hopkins University Press) [Google Scholar]
- Gouttebroze, P. 1986, A&A, 160, 195 [NASA ADS] [Google Scholar]
- Hashemi, B., & Trefethen, L. N. 2017, SIAM J. Sci. Comput., 39, C341 [CrossRef] [Google Scholar]
- Hummer, D. G. 1962, MNRAS, 125, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., & Paganini, A. 2018, ApJ, 857, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Janett, G., Carlin, E. S., Steiner, O., & Belluzzi, L. 2017, ApJ, 840, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Kano, R., Trujillo Bueno, J., Winebarger, A., et al. 2017, ApJ, 839, L10 [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Klumer Academic Publishers) [Google Scholar]
- Nagendra, K. N., & Sampoorna, M. 2011, A&A, 535, A88 [CrossRef] [EDP Sciences] [Google Scholar]
- Paganini, A., & Hashemi, B. 2020, Software to Compute Chebfun-based Approximations of Angle-averaged Redistribution Functions [Google Scholar]
- Rees, D. E., & Saliba, G. J. 1982, A&A, 115, 1 [NASA ADS] [Google Scholar]
- Sampoorna, M., Nagendra, K. N., & Stenflo, J. O. 2017, ApJ, 844, 97 [CrossRef] [Google Scholar]
- Sampoorna, M., Nagendra, K. N., Sowmya, K., Stenflo, J. O., & Anusha, L. S. 2019, ApJ, 883, 188 [CrossRef] [Google Scholar]
- Trujillo Bueno, J. 2014, in Solar Polarization 7, eds. K. N. Nagendra, J. O. Stenflo, Z. Q. Qu, & M. Sampoorna, ASP Conf. Ser., 489, 137 [Google Scholar]
- Trujillo Bueno, J., Štěpán, J., Belluzzi, L., et al. 2018, ApJ, 866, L15 [CrossRef] [Google Scholar]
- Uitenbroek, H. 1989, A&A, 216, 310 [NASA ADS] [Google Scholar]
Appendix A: Expression of the angle-averaged redistribution matrix for a two-level atom
As shown in detail in Alsina Ballester et al. (2017), in the polarized case, the angle-averaged redistribution matrix for a two-level atom with an unpolarized and infinitely sharp lower level, in the presence of magnetic fields, is given by
where the indices K and K′ can take values 0, 1, and 2, while Q can take integer values between −Kmin and +Kmin, with Kmin = min(K, K′).
The 4 × 4 matrices 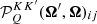 generalize to the polarized case (within the framework of the irreducible spherical tensors formalism) the angular phase function appearing in Eq. (2). In a reference system such that the z-axis (quantization axis) is directed along the magnetic field, they are given by
generalize to the polarized case (within the framework of the irreducible spherical tensors formalism) the angular phase function appearing in Eq. (2). In a reference system such that the z-axis (quantization axis) is directed along the magnetic field, they are given by
where 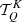 is the so-called polarization tensor (see Landi Degl’Innocenti & Landolfi 2004). The expression of
is the so-called polarization tensor (see Landi Degl’Innocenti & Landolfi 2004). The expression of 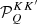 in an arbitrary reference system can be found through simple rotations (e.g., Alsina Ballester et al. 2017).
in an arbitrary reference system can be found through simple rotations (e.g., Alsina Ballester et al. 2017).
The quantities ![$ \left[\mathcal{R}_{\mathrm{II-AA}} \right]^{KK^\prime}_Q $](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq48.gif) are given by (see Alsina Ballester et al. 2017)
are given by (see Alsina Ballester et al. 2017)
where we have introduced the Faddeeva function
and Mu, 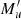 , Mℓ,
, Mℓ, 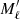 are the magnetic quantum numbers corresponding to the various substates of the upper (subscript u) and lower (subscript ℓ) levels. The quantity gu is the Landé factor of the upper level, ωL is the angular Larmor frequency (which depends on the magnetic field intensity), and 𝒞 is a factor related to the coupling of the various magnetic quantum numbers (for its explicit expression see Bommier 1997). The integers p, p′,p″, and p′″ it contains range from −1 to 1. The frequency shifts of the Zeeman transition between the upper level with Mu and the lower level with Mℓ, with respect to the line-center frequency ν0 are given by
are the magnetic quantum numbers corresponding to the various substates of the upper (subscript u) and lower (subscript ℓ) levels. The quantity gu is the Landé factor of the upper level, ωL is the angular Larmor frequency (which depends on the magnetic field intensity), and 𝒞 is a factor related to the coupling of the various magnetic quantum numbers (for its explicit expression see Bommier 1997). The integers p, p′,p″, and p′″ it contains range from −1 to 1. The frequency shifts of the Zeeman transition between the upper level with Mu and the lower level with Mℓ, with respect to the line-center frequency ν0 are given by
whereas the frequency splittings between two lower levels with Mℓ and 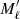 are given by
are given by
where E(M) is the energy of a given magnetic sublevel, h is the Planck constant, and ΔνD is the Doppler width of the line.
One can immediately realize that the quantity shown in Eq. (A.3) may be expressed in terms of the functions f and h given in Eqs. (5) and (6) as
where the dependence on the involved states is included in the variables
It is interesting to observe that if the magnetic fields and the polarization of the radiation are neglected, the expressions of Eqs. (2) and (3) are recovered. Indeed, when there is no magnetic splitting of the Zeeman sublevels, the arguments of the various functions f and h are all equal for any given u and u′. Thus, the various contributions from the functions h cancel each other, and the imaginary part of Eq. (A.3) vanishes. Moreover, when such splittings are absent, it is possible to perform the following sum over the magnetic quantum numbers,
where WK is a factor characterizing the polarizability of the considered line (see Landi Degl’Innocenti & Landolfi 2004), and Ju and Jℓ are the total angular momenta of the upper and lower level, respectively. Observing that in the absence of magnetic fields ωL = 0, the quantity ![$ \left[\mathcal{R}_{\mathrm{II-AA}}\right]^{K K^\prime}_Q $](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq60.gif) thus reduces to
thus reduces to
In the particular case of a transition with Jℓ = 0 and Ju = 1 (whose results correspond to the semi-classical picture), the factors WK are all equal to unity, so that (A.10) has no dependence on K and reduces to (2), valid in the unpolarized case. Summing over the components of the angular phase matrix and neglecting the polarization of the radiation field, one recovers the dipole scattering angular phase function
with Θ the scattering angle. If, in addition, the incident radiation field is isotropic, then (B.1) introduces a δK0 δQ0 (i.e., the only nonzero multipolar component of the radiation field tensor is 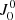 ). Thus, the only term of the previous sum that contributes to the emissivity is
). Thus, the only term of the previous sum that contributes to the emissivity is
which represents the angular phase function for isotropic scattering.
Appendix B: Numerical evaluation of the emission coefficient in the polarized case
The method introduced in Sect. 5 for the numerical evaluation of the frequency integral of Eq. (1) can be easily generalized from the unpolarized to the polarized case (see Eq. (4)). As a first step, we substitute Eq. (A.2) into Eq. (A.1) and we introduce the radiation field tensor
We note that 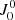 corresponds to the mean intensity given in Eq. (18). The emission coefficient for the polarized case, given in Eq. (4), can thus be written as
corresponds to the mean intensity given in Eq. (18). The emission coefficient for the polarized case, given in Eq. (4), can thus be written as
where the 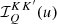 represents an extension to the polarized case of the scattering integral of Eq. (19):
represents an extension to the polarized case of the scattering integral of Eq. (19):
From Eq. (A.6) it is immediate to realize that quantities of the form (B.3) can be expressed as linear combinations of functions of the form
In order to simplify the notation, in the previous expressions we have introduced the label α to indicate the set of states with magnetic quantum numbers Mℓ (initial), 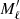 (final), and Mu. The arguments in the function f and h are xα = xℓℓ′ and yα = yuℓℓ′.
(final), and Mu. The arguments in the function f and h are xα = xℓℓ′ and yα = yuℓℓ′.
In full analogy with Sect. 5, given a reduced frequency grid {ui} and an interpolatory basis {bj(u′)}, the interpolant for the 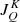 components can be written as
components can be written as
By using this interpolation, the quantities appearing in Eqs. (B.4) and (B.5) can be approximated as
where we have introduced the weights
in which xα, i and yα, i are variables xα and yα with u = ui in Eqs. (A.7) and (A.8). As in Sect. 5, it is apparent that the evaluation of these weights represents the majority of the computational cost involved in the frequency integral for the polarized emission coefficient. This involves the computation of distinct F and H weights for each set of states α, which differ from each other in the evaluation of the functions f and h at different xα, i and yα, i points.
All Figures
 |
Fig. 1. Plot of log10f(x, y, a) for a = 10−3 and x, y ∈ [0, 10]. The two bold lines indicate the f = 10−10 and the f = 10−20 contours. Image values smaller than 10−30 are not plotted. We observe a rapid decay in the x direction. The qualitative behavior of log10f is similar for a ∈ [10−5, 10−1]. |
| In the text | |
 |
Fig. 2. Plot of the integrand of Eq. (5) versus γ for different values of x, y, and a. |
| In the text | |
 |
Fig. 3. Gauss quadrature error in approximating f. The number of quadrature points necessary to achieve machine precision depends on the values of x, y, and a. |
| In the text | |
 |
Fig. 4. Coefficients of the polynomials ci (Cols), sj (Rows), and tk (Tubes) from Eq. (10). |
| In the text | |
 |
Fig. 5. Quantiles of the sampled error defined in Eq. (11). |
| In the text | |
 |
Fig. 6. Quantiles of the sampled rescaled error defined in Eq. (15). |
| In the text | |
 |
Fig. 7. Quantiles of the sampled error of Eq. (16). |
| In the text | |
 |
Fig. 8. Quantiles of the sampled error of Eq. (17). |
| In the text | |
 |
Fig. 9. Self-comparison error versus computational time of Chebfun-based and quadrature-based approximations of f on 4005 × 10, 20, 40 quadrature points. The circles on the curves for quadrature-based solutions indicate, for decreasing error, the results obtained taking 8, 16, 32, 64, 128, and 256 quadrature points. The circles on the curves for Chebfun solutions indicate, for decreasing error, the results obtained taking eps = 10−5, 10−6, 10−7, 10−8, 10−9, and 10−10. |
| In the text | |
 |
Fig. 10. Cross-comparison error versus computational time of Chebfun-based and quadrature-based approximations of f on 4005 × 10, 20, 40 quadrature points. The circles on the curves for quadrature-based solutions indicate, for decreasing error, the results obtained taking 8, 16, 32, 64, 128, 256, and 512 quadrature points. The circles on the curves for Chebfun solutions indicate, for decreasing error, the results obtained taking eps = 10−5, 10−6, 10−7, 10−8, 10−9, 10−10, and 10−11. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\mathcal{R} _{\mathrm{II-AA} } (u^\prime ,u) = \frac{\Gamma _{\rm R}}{\Gamma _{\rm R} + \Gamma _{\rm I} + \Gamma _{\rm E}} \, \nonumber \\&\qquad \qquad \qquad \times \frac{1}{2 \pi } \int _0^{\pi }\mathrm{d}\Theta \exp {\left[ -\left( \frac{u^\prime -u}{2 \sin {\Theta /2}} \right)^2 \right]} \nonumber \\&\qquad \qquad \qquad \qquad \qquad \times H \left(\frac{a}{\cos {\Theta /2}},\frac{u+u^\prime }{2 \cos {\Theta /2}}\right) , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq3.gif)
![$$ \begin{aligned} \varepsilon _i(u,\boldsymbol{\Omega })\! = \!k_L\! \int _{-\infty }^{\infty } \!\! \mathrm{d} u^\prime \! \oint \frac{\mathrm{d} \boldsymbol{\Omega }^\prime }{4 \pi }\! \sum _{j=0}^3 \left[ R(u^\prime ,\boldsymbol{\Omega }^\prime ,u,\boldsymbol{\Omega }) \right]_{ij} I_j(u^\prime ,\boldsymbol{\Omega }^\prime ) , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq4.gif)
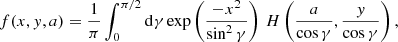
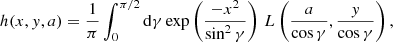
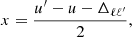
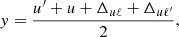
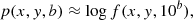
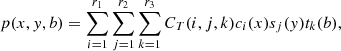
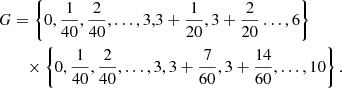
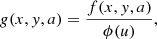
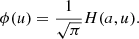
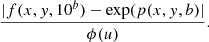
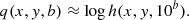
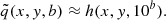
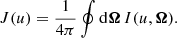
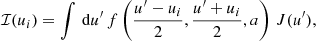

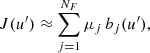
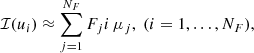
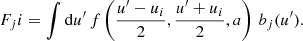
![$$ \begin{aligned} b_j(x) = {\left\{ \begin{array}{ll} \frac{x-u_{j-1}}{u_j-u_{j-1}} ,&x\in (u_{j-1},u_j] \\ \frac{u_{j+1}-x}{u_{j+1}-u_{j}} ,&x\in (u_{j},u_{j+1}] \\ 0,&\text{otherwise.} \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq39.gif)
![$$ \begin{aligned} b_1(x) = {\left\{ \begin{array}{ll} 1 ,&u \le u_1 \\ \frac{u_{2}-x}{u_{2}-u_{1}} ,&x\in (u_{1}, u_{2}] \\ 0,&\text{otherwise} \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq40.gif)
![$$ \begin{aligned} b_{N_F}(x) = {\left\{ \begin{array}{ll} \frac{x-u_{N_F-1}}{u_{N_F}-u_{N_F-1}} ,&x\in (u_{N_F-1},u_{N_F}]\\ 1 ,&x> u_{N_F} \\ 0,&\text{otherwise,} \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq41.gif)
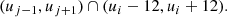
![$$ \begin{aligned}&\left[ R_{\mathrm{II-AA} }(u^\prime ,\boldsymbol{\Omega }^\prime ,u,\boldsymbol{\Omega }) \right]_{i j} = \nonumber \\&\qquad \qquad \qquad \sum _{K K^\prime Q} \left[\mathcal{R} _\mathrm{II-AA} \right]^{K K^\prime }_Q \! (u^\prime ,u) \, \mathcal{P} ^{K K^\prime }_Q(\boldsymbol{\Omega }^{\prime },\boldsymbol{\Omega })_{ij} , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq43.gif)
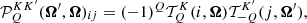
![$$ \begin{aligned}&\left[ {\mathcal{R} }_{\mathrm{II-AA} } \right]^{K K^\prime }_Q \! (u^\prime ,u) \, = \nonumber \\&\qquad \sum _{\begin{matrix} M_u M_u^\prime M_\ell M_\ell ^\prime \\ p \, p^\prime p^{\prime \prime } p^{\prime \prime \prime } \end{matrix}} \frac{\Gamma _R}{\Gamma _R + \Gamma _E + \Gamma _I + \mathrm{i} \, \omega _L g_{u} Q} \nonumber \\&\qquad \times {\mathcal{C} }_{K K^\prime Q M_u M_u^\prime M_\ell M_\ell ^\prime \, p p^\prime p^{\prime \prime } p^{\prime \prime \prime }} \nonumber \\&\qquad \times \frac{1}{2\pi } \int _0^\pi \!\!\mathrm{d} \Theta \exp \left[-\left(\frac{u^\prime - u - \Delta _{M_\ell M^\prime _{\ell }}}{2\sin (\Theta /2)} \right)^2 \right] \nonumber \\&\qquad \times \frac{1}{2} \Biggl \{ W\left(\frac{a}{\cos (\Theta /2)}, \frac{u + u^\prime + \Delta _{M^\prime _{u} M_\ell } + \Delta _{M^\prime _{u} M^\prime _{\ell }}}{2 \cos (\Theta /2)} \right) \nonumber \\&\qquad \quad \, + W\left(\frac{a}{\cos (\Theta /2)}, \frac{u + u^\prime + \Delta _{M_{u} M_\ell } + \Delta _{M_{u} M^\prime _{\ell }}}{2 \cos (\Theta /2)} \right)^*\Biggr \} , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq49.gif)
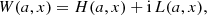
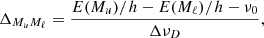
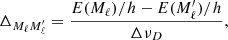
![$$ \begin{aligned}&\left[ {\mathcal{R} }_{\mathrm{II-AA} } \right]^{K K^\prime }_Q \! (u^\prime ,u) \, = \nonumber \\&\qquad \sum _{\begin{matrix} M_u M_u^\prime M_\ell M_\ell ^\prime \\ p \, p^\prime p^{\prime \prime } p^{\prime \prime \prime } \end{matrix}} \frac{\Gamma _R}{\Gamma _R + \Gamma _E + \Gamma _I + \mathrm{i} \, \omega _L g_{u} Q} \nonumber \\&\qquad \times {\mathcal{C} }_{K K^\prime Q M_u M_u^\prime M_\ell M_\ell ^\prime \, p p^\prime p^{\prime \prime } p^{\prime \prime \prime }} \nonumber \\&\qquad \times \frac{1}{2} \biggl [ f(x_{\ell \ell ^\prime },y_{u^\prime \ell \ell ^\prime },a) + f(x_{\ell \ell ^\prime },y_{u \ell \ell ^\prime }, a) \nonumber \\&\qquad \quad \ + \mathrm{i} \Big ( h(x_{\ell \ell ^\prime },y_{u^\prime \ell \ell ^\prime },a) - h(x_{\ell \ell ^\prime },y_{u \ell \ell ^\prime },a) \Big ) \biggr ] , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq56.gif)
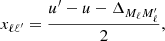
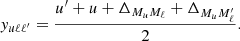
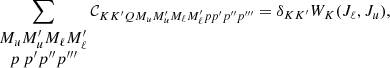
![$$ \begin{aligned} \left[\mathcal{R} _{\mathrm{II-AA} }\right]^{K}(u^\prime ,u) = \frac{\Gamma _R}{\Gamma _R + \Gamma _E + \Gamma _I} W_K(J_\ell ,J_u) \, f(x,y,a) . \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq61.gif)
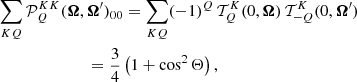
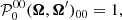
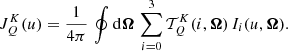
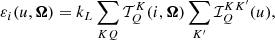
![$$ \begin{aligned} \mathcal{I} ^{K K^\prime }_Q(u) = \, (-1)^Q \, \int _{-\infty }^\infty \mathrm{d}u^\prime \, \left[\mathcal{R} _{\mathrm{II-AA} } \right]^{K K^\prime }_Q \! (u^\prime ,u) J^{K^\prime }_{-Q}(u^\prime ) . \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq69.gif)
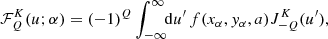
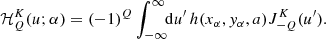
![$$ \begin{aligned} J^K_Q(u^\prime ) \approx \sum _{j=1}^{N_F} \left[\mu ^K_Q \right]_j \, b_{j}(u^{\prime }) . \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq74.gif)
![$$ \begin{aligned} \mathcal{F} ^K_Q(u_i; \alpha ) \approx (-1)^Q \sum _{j=1}^{N_F} \left[{F}\right]^{\alpha }_{j i} \left[\mu ^K_{-Q} \right]_j , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq75.gif)
![$$ \begin{aligned} \mathcal{H} ^K_Q(u_i; \alpha ) \approx (-1)^Q \sum _{j=1}^{N_F} \left[{H}\right]^{\alpha }_{j i} \left[\mu ^K_{-Q} \right]_j , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq76.gif)
![$$ \begin{aligned}&\left[{F}\right]^{\alpha }_{j i} = \int _{-\infty }^\infty \!\! \mathrm{d} u^\prime f(x_{\alpha , i}, y_{\alpha , i}, a) \, b_j(u^\prime ) , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq77.gif)
![$$ \begin{aligned}&\left[{H}\right]^{\alpha }_{j i} = \int _{-\infty }^\infty \!\! \mathrm{d} u^\prime h(x_{\alpha , i}, y_{\alpha , i}, a) \, b_j(u^\prime ) , \end{aligned} $$](/articles/aa/full_html/2021/01/aa37149-19/aa37149-19-eq78.gif)