| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628501 | |
| Published online | 25 May 2016 | |
Transverse oscillations and stability of prominences in a magnetic field dip
1 Centre for Fusion, Space and Astrophysics, Department of
Physics, University of Warwick, CV4 7AL, UK
e-mail:
D.Kolotkov@warwick.ac.uk
2
School of Space Research, Kyung Hee University,
Yongin, 446-701
Gyeonggi,
Korea
3
Central Astronomical Observatory at Pulkovo of the Russian Academy
of Sciences, 196140
St. Petersburg,
Russia
Received: 12 March 2016
Accepted: 13 April 2016
Aims. We developed an analytical model of the global transverse oscillations and mechanical stability of a quiescent prominence in the magnetised environment with a magnetic field dip that accounts for the mirror current effect.
Methods. The model is based on the interaction of line currents through the Lorentz force. Within this concept the prominence is treated as a straight current-carrying wire, and the magnetic dip is provided by two photospheric current sources.
Results. Properties of both vertical and horizontal oscillations are determined by the value of the prominence current, its density and height above the photosphere, and the parameters of the magnetic dip. The prominence can be stable in both horizontal and vertical directions simultaneously when the prominence current dominates in the system and its height is less than the half-distance between the photospheric sources.
Key words: Sun: filaments, prominences / Sun: magnetic fields / Sun: oscillations
© ESO, 2016
1. Introduction
Coronal mass ejections (CMEs) are known to be the most powerful and geoeffective phenomena occurring in the solar atmosphere. An important role in their initiation is assigned to the evolution of prominences, cold and dense plasma filaments levitating in the magnetised environment of the solar corona. An important feature in the evolution of prominences is their oscillations. Global collective oscillations of prominences are seen to have periods ranging from a few tens of minutes to several hours (e.g. Mashnich & Bashkirtsev 1990; Bashkirtsev & Mashnich 1993; Oliver & Ballester 2002; Arregui et al. 2012). Both vertically (e.g. Bocchialini et al. 2011; Kim et al. 2014) and horizontally polarised (e.g. Kleczek & Kuperus 1969; Molowny-Horas et al. 1997; Tripathi et al. 2009) motions of prominences have been observed. In some cases the oscillations occur before prominence eruptions (e.g. Isobe & Tripathi 2006), or are excited by an Extreme Ultraviolet (EUV) wave (e.g. Hershaw et al. 2011; Asai et al. 2012; Shen et al. 2014a,b).
Vertical transverse oscillations of prominences have been modelled based on natural magnetohydrodynamic (MHD) oscillations of the current-carrying toroidal magnetic ropes (Cargill et al. 1994; Vršnak 2008). Theoretical aspects of non-radial motions of an eruptive filament also modelled as toroidal currents are discussed by Filippov et al. (2001). In addition, comparison of the modelling and observational results showed that the equilibrium state is most likely supported by the potential magnetic field structures with a magnetic dip (see e.g. Filippov 2016, for recent results). This Kippenhahn-Schlüter type equilibrium of prominences (Kippenhahn & Schlüter 1957) was used in theoretical models treating the prominence as a plasma slab embedded in a magnetic dip created by some sources at the surface of the Sun. In particular, MHD eigen modes of such a prominence structure, i.e. the fast and slow magnetoacoustic and Alfvén modes, with and without accounting for the gravity force, were investigated in Oliver et al. (1993) and Joarder & Roberts (1993), respectively. Global oscillations of prominences also modelled as a plasma slab in a magnetic dip with straight magnetic field lines anchored in vertical rigid boundaries (not connected to the solar surface) are considered in Anzer (2009). Properties of MHD oscillations as perturbations of a two-dimensional magnetostatic model of a prominence, taking into account the effects of gravity, were determined numerically in Terradas et al. (2013). Large-amplitude longitudinal oscillations in prominences were modelled in terms of a so-called pendulum model by Luna & Karpen (2012) and Luna et al. (2016). That model has been successfully adapted for a dipped magnetic field line configuration, and treats the gravity projected along the magnetic field lines as the restoring force.
Another essentially different approach describing quiescent prominence oscillations, based on the interaction of line currents through the electromagnetic Lorentz force, was suggested by Kuperus & Raadu (1974, the KR model). In this mechanism the prominence is modelled as a straight current-carrying wire located at a height above the conductive photosphere. Interaction of the prominence current with the conductive surface is described by the introduction of a virtual mirror current (known as the mirror effect) located below the photosphere, strictly symmetric with respect to the prominence. The KR model allows for the vertical oscillations of the prominence, and does not describe horizontally polarised oscillations. Indeed, even a small displacement of the prominence current in the horizontal direction automatically causes a corresponding identical displacement of the mirror current, and thus the horizontal restoring force is always absent from that model. Moreover, the KR model neglects the interaction of the prominence with external sources of the magnetic field. In particular, the prominence may be embedded in a magnetic dip, e.g. a Kippenhahn–Schlüter type magnetic configuration. In this case there could be restoring forces responsible for horizontal oscillations. Effects of the delayed response between the photosphere and the filament were also investigated within the concept of line current models in van den Oord et al. (1998). In particular, it was shown that the Kippenhahn–Schlüter type equilibrium of a prominence can never be stable in the horizontal and vertical directions simultaneously, i.e. the prominence position is always unstable if the effect of the mirror current is neglected in the model.
In this paper we developed an analytical model for oscillatory dynamics of a prominence in a magnetic environment accounting for both the magnetic dip and mirror current effects. The dip is provided by two photospheric current sources (Fig. 1). We considered vertically and horizontally polarised oscillations of the prominence in such a magnetic topology, analytically deriving equations of motion and determining the oscillation periods. We also analysed the stability of this configuration. In particular, we showed that in contrast to the results obtained in van den Oord et al. (1998), the prominence can be stable in both the horizontal and vertical directions simultaneously if the effect of the mirror force is accounted for in the model. Possible seismological applications of the developed model are also discussed.
2. Model, forces, and equilibrium
The magnetic field topology with a magnetic dip (Fig. 1) is configured by two co-aligned spatially separated photospheric currents (with d being the half-distance between the currents) of the same magnitude I. The prominence itself is modelled as a massive straight wire representing a magnetic rope with a current i which is located at a height h above the photosphere. In turn, it causes a so-called mirror current (see the KR model) due to conductive properties of the photosphere. By its definition, the mirror current is oppositely directed with respect to the prominence current i, has the same magnitude, and is located at the distance 2 h strictly below the prominence current (see Fig. 1). In this model the prominence can interact with the coronal surroundings through the corresponding mutual interaction of the magnetic fields produced by the prominence i and photospheric I currents.
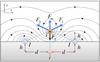 |
Fig. 1 Massive prominence with a line current i located at the height h above the photosphere in the magnetic dip configured by two photospheric currents I, with d being the half-distance between the currents. The mirror current i generated by the conductive properties of the photosphere is located strictly below the prominence. The field lines of the total magnetic field produced by the photospheric, mirror, and prominence sources are shown for h = 0.5 d and i = 0.5 I. |
The equilibrium of a prominence in such a magnetic environment is provided by the Lorentz and gravity forces balance 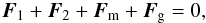 (1)where F1 = F2 = k1/ (d2 + h2)1/2 are the Lorentz forces per unit length acting between the photospheric currents I and the prominence current i, with k1 = μ0Ii/ 2π; Fm = k2/ 2 h is the mirror force between the prominence and the mirror current, with k2 = μ0i2/ 2π; and Fg = ρg is the gravity force which is assumed to be constant in the model, with ρ being a linear mass density of the prominence (its volume mass density multiplied by the cross-sectional area), measured in kg m-1. According to the definition of the mirror current, we note that the mirror force Fm acting on the prominence is always directed upwards and strictly along the vertical axis and cannot contribute to the horizontal dynamics of the prominence.
(1)where F1 = F2 = k1/ (d2 + h2)1/2 are the Lorentz forces per unit length acting between the photospheric currents I and the prominence current i, with k1 = μ0Ii/ 2π; Fm = k2/ 2 h is the mirror force between the prominence and the mirror current, with k2 = μ0i2/ 2π; and Fg = ρg is the gravity force which is assumed to be constant in the model, with ρ being a linear mass density of the prominence (its volume mass density multiplied by the cross-sectional area), measured in kg m-1. According to the definition of the mirror current, we note that the mirror force Fm acting on the prominence is always directed upwards and strictly along the vertical axis and cannot contribute to the horizontal dynamics of the prominence.
The system is completely defined by the geometrical parameters h and d, and magnetic constants k1 and k2 (written in terms of I and i), while the appropriate mass density ρ of the prominence necessary for its vertical equilibrium, is determined by the following condition (2). However, for seismological purposes it is also useful to re-write this condition through the parameters h and ρ, assuming a priori that they are available from observations: 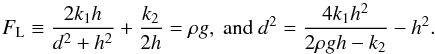 (2)The horizontal equilibrium of the prominence in turn is not affected by the essentially vertical forces Fm and Fg, and is provided automatically by the balance between the horizontal components of F1 and F2 because of the horizontal symmetry of the model. Equations (2) put the first constraint on the parameters of the model. Indeed, for a given distance d to have a real value in the equilibrium condition, the parameters need to be related as
(2)The horizontal equilibrium of the prominence in turn is not affected by the essentially vertical forces Fm and Fg, and is provided automatically by the balance between the horizontal components of F1 and F2 because of the horizontal symmetry of the model. Equations (2) put the first constraint on the parameters of the model. Indeed, for a given distance d to have a real value in the equilibrium condition, the parameters need to be related as 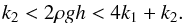 (3)Inequality (3) describes a condition necessary for the equilibrium of the prominence to exist, between its gravitational energy and the total magnetic energy (written in terms of k1 and k2), generated by the prominence and photospheric currents, i and I, respectively. Thus, when 2ρgh> 4k1 + k2, the magnetic background cannot sustain the prominence and it falls to the surface. In the other case, when 2ρgh<k2, the prominence’s magnetic energy exceeds the gravitational energy and the prominence lifts off.
(3)Inequality (3) describes a condition necessary for the equilibrium of the prominence to exist, between its gravitational energy and the total magnetic energy (written in terms of k1 and k2), generated by the prominence and photospheric currents, i and I, respectively. Thus, when 2ρgh> 4k1 + k2, the magnetic background cannot sustain the prominence and it falls to the surface. In the other case, when 2ρgh<k2, the prominence’s magnetic energy exceeds the gravitational energy and the prominence lifts off.
 |
Fig. 2 Magnetic force FL (2) acting upwards on the unperturbed prominence for different values of the prominence i and photospheric I currents. The horizontal dotted line shows a constant gravity force ρg needed to satisfy equilibrium condition (2). This example shows that the system may have up to three different equilibria (blue asterisks) depending upon the values of the parameters of the model. |
According to Eq. (2), the vertical component of the total Lorentz force acting on an unperturbed prominence, FL gradually decreases with height for all values of the photospheric currents I being lower than or equal to the prominence current i, and may have both negative and positive gradients for I>i. Consequently, for I<i the system is able to have only a single equilibrium determined by the FL = ρg balance, while for I>i there are at most three possibilities to satisfy the force balance condition, and hence, up to three equilibria of the system at different heights may exist. Corresponding examples are shown in Fig. 2 for different values of the I/i ratio.
For the case when the prominence is obliquely perturbed by a small displacement with corresponding x and z components, the equation of motion of the prominence can be written in a vector form as ![\begin{equation} \label{motion} \rho\left[\ddot{x}\,\vec{e}_x+\ddot{z}\,\vec{e}_z\right]=F_x\,\vec{e}_x+F_z\,\vec{e}_z, \end{equation}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq34.png) (4)where ex and ez are unit vectors in the positive x- and z-directions, and
(4)where ex and ez are unit vectors in the positive x- and z-directions, and ![\begin{eqnarray} \label{Fx} F_x&=&\frac{2k_1x[(h+z)^2+x^2-d^2]}{(d^2-x^2)^2+2(d^2+x^2)(h+z)^2+(h+z)^4} \nonumber\\ && \approx \frac{2k_1(h^2-d^2)}{(d^2+h^2)^2}\,x, \\\label{Fz} F_z&=&\frac{2k_1(h+z)[d^2+x^2+(h+z)^2]}{(d^2-x^2)^2+2(d^2+x^2)(h+z)^2+(h+z)^4}+\frac{k_2}{2h+z}-\rho g \nonumber\\ &&\approx \left[\frac{2k_1(d^2-h^2)}{(d^2+h^2)^2}-\frac{k_2}{4h^2}\right]z \end{eqnarray}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq37.png) are the projections of the total force given in Eq. (1) on the x-axis (horizontal) and z-axis (vertical), expanded up to the first order of the small perturbations, x and z. We note that the first-order Taylor expansion in Eq. (6) was derived taking into account condition (2) for the vertical equilibrium of the prominence. Because we restrict our attention to linear perturbations only, both forces Fx (5) and Fz (6) lose their dependence on z and x, respectively, and horizontally and vertically polarised oscillations are independent of each other and hence can be considered separately.
are the projections of the total force given in Eq. (1) on the x-axis (horizontal) and z-axis (vertical), expanded up to the first order of the small perturbations, x and z. We note that the first-order Taylor expansion in Eq. (6) was derived taking into account condition (2) for the vertical equilibrium of the prominence. Because we restrict our attention to linear perturbations only, both forces Fx (5) and Fz (6) lose their dependence on z and x, respectively, and horizontally and vertically polarised oscillations are independent of each other and hence can be considered separately.
3. Vertically polarised oscillations
We consider the case when the initial displacement of the prominence is directed strictly along the vertical z-axis, i.e. we assume x = 0 and z ≠ 0 in Eq. (4). In this case, the vertical component (6) of the total force acting on the prominence has the form 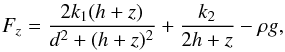 (7)where the first term on the right-hand side corresponds to the Lorentz force acting on the perturbed prominence from two photospheric currents, the second term is the corresponding mirror force, and the last term is the constant gravity force.
(7)where the first term on the right-hand side corresponds to the Lorentz force acting on the perturbed prominence from two photospheric currents, the second term is the corresponding mirror force, and the last term is the constant gravity force.
With the use of the first-order Taylor expansion of the perturbed vertical force Fz written in Eq. (6), the equation of motion of the prominence along the vertical axis is 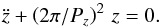 (8)Equation (8) is a harmonic oscillator equation and describes small-amplitude vertically polarised oscillations of the prominence with the period (expressed either in terms of h and d or via ρ and h):
(8)Equation (8) is a harmonic oscillator equation and describes small-amplitude vertically polarised oscillations of the prominence with the period (expressed either in terms of h and d or via ρ and h): ![\begin{eqnarray} \label{periodz} P_z&=&P_{\rm KR}\left[1+8\frac{k_1}{k_2}\frac{h^2(h^2-d^2)}{(d^2+h^2)^2}\right]^{-1/2}\nonumber\\ &=&\frac{P_{\rm KR}\,\sqrt{k_1k_2}}{\left[(2\rho gh-k_2)^2-2k_2(2\rho gh-k_2)+k_1k_2\right]^{1/2}}, \end{eqnarray}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq44.png) (9)where d2 in form (2) has been substituted, and
(9)where d2 in form (2) has been substituted, and 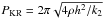 is the period of prominence oscillations in the absence of the photospheric current effect (i.e. the limiting case corresponding to the KR model). In fact, neither k1 nor k2 (i.e. the currents I and i) can have zero values in our model. However, the period (9) can be reduced to the KR limit when the half-distance d between the external currents tends to infinity. This limiting case can be achieved when 2ρgh = k2 (see Eq. (2)). In other cases, period (9) has a non-trivial dependence upon the currents I and i, height h, and mass density ρ. Its dependence upon the currents ratio I/i (i.e. k1/k2) for different values of 2ρgh/k2 (also including the KR limit 2ρgh = k2) is shown in Fig. 3.
is the period of prominence oscillations in the absence of the photospheric current effect (i.e. the limiting case corresponding to the KR model). In fact, neither k1 nor k2 (i.e. the currents I and i) can have zero values in our model. However, the period (9) can be reduced to the KR limit when the half-distance d between the external currents tends to infinity. This limiting case can be achieved when 2ρgh = k2 (see Eq. (2)). In other cases, period (9) has a non-trivial dependence upon the currents I and i, height h, and mass density ρ. Its dependence upon the currents ratio I/i (i.e. k1/k2) for different values of 2ρgh/k2 (also including the KR limit 2ρgh = k2) is shown in Fig. 3.
 |
Fig. 3 Left: period Pz (9) of vertical oscillations of a prominence vs. the currents ratio I/i for different values of the dimensionless parameter a = 2ρgh/k2. We note that the case a = 1 corresponds to the KR limit (Kuperus & Raadu 1974) when the effect of the photospheric currents is negligibly small. Right: period Px (13) of horizontal oscillations depending upon the same parameters I/i and a as shown in the left panel. Dashed lines in both panels show a threshold values of I/i where periods (9) and (13) become imaginary, and corresponding instabilities develop. |
General dependence of the vertical dynamics of the prominence described by Eq. (8) on the parameters of the model can also be derived analytically. More specifically, when the prominence current dominates in the system, i.e. 0 <k1/k2< 1, Eq. (8) shows solutions that are always stable for the vertical displacement. The particular case when the prominence i and photospheric I currents are of the same magnitude, i.e. k1 = k2 ≡ k, also corresponds to the always stable state of the prominence oscillating harmonically around the equilibrium position with a period P = PKR | (d2 + h2)/(3h2 − d2) |. In both of these cases, only conditions (2) and (3), which provide the existence of an initial equilibrium of the system, should be satisfied for h and d. In contrast, for the photospheric currents domination (k1/k2> 1) there is a parametric region of a vertical instability (see Fig. 4) determined by condition (3) and the following relations (written either in terms of h and d or via ρ and h): ![\begin{eqnarray} \label{condz} &&\frac{d\sqrt{k_2}}{\left[4k_1\!-\!k_2\!+\!4\sqrt{k_1^2-k_1k_2}\right]^{1/2}}< h<\frac{d\sqrt{k_2}}{\left[4k_1\!-\!k_2\!-\!4\sqrt{k_1^2-k_1k_2}\right]^{1/2}},\nonumber\\ &&\mathrm{or}~~k_1+k_2-\sqrt{k_1^2-k_1k_2}<2\rho gh<k_1+k_2+\sqrt{k_1^2-k_1k_2}. \end{eqnarray}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq59.png) (10)
(10)
 |
Fig. 4 Parametric regions of the prominence instability, determined by equilibrium condition (3), (10) (vertical instability), (14) (horizontal instability). Left and right panels show the corresponding regions determined via ρ and h, and h and d, respectively. |
4. Horizontally polarised oscillations
We now consider the case when z = 0, i.e. the initial displacement of the prominence is directed strictly along the horizontal x-axis. In this case the force Fx (5) acting on the prominence along the horizontal axis reduces to ![\begin{equation} \label{Fx2} F_x=\frac{2k_1x[h^2-d^2+x^2]}{(d^2-x^2)^2+2(d^2+x^2)h^2+h^4}\cdot \end{equation}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq61.png) (11)Using the Taylor expansion of the force Fx up to the first order of the small perturbations (x and z) given in (5), the equation of motion describing small-amplitude dynamics of the prominence along the horizontal axis is
(11)Using the Taylor expansion of the force Fx up to the first order of the small perturbations (x and z) given in (5), the equation of motion describing small-amplitude dynamics of the prominence along the horizontal axis is 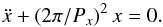 (12)Similar to the vertically polarised oscillatory modes described in the previous section, Eq. (12) shows harmonic oscillations of the prominence around the equilibrium position (x = 0 and z = 0), with the period Px,
(12)Similar to the vertically polarised oscillatory modes described in the previous section, Eq. (12) shows harmonic oscillations of the prominence around the equilibrium position (x = 0 and z = 0), with the period Px, ![\begin{eqnarray} \label{periodx} P_x&=&P_{\rm KR}\sqrt{\frac{k_2}{8k_1}\frac{(d^2+h^2)^2}{h^2(d^2-h^2)}}\nonumber\\ &=&\frac{P_{\rm KR}\,\sqrt{k_1k_2}}{\left[2k_1(2\rho gh-k_2)-(2\rho gh-k_2)^2\right]^{1/2}}\cdot \end{eqnarray}](/articles/aa/full_html/2016/06/aa28501-16/aa28501-16-eq63.png) (13)In the KR limit that can be achieved when 2ρgh = k2 (see Eq. (2)), we note that the value of Px tends to infinity. Behaviour of the period (13) for various other values of ratios 2ρgh/k2 and I/i is shown in Fig. 3.
(13)In the KR limit that can be achieved when 2ρgh = k2 (see Eq. (2)), we note that the value of Px tends to infinity. Behaviour of the period (13) for various other values of ratios 2ρgh/k2 and I/i is shown in Fig. 3.
The regions on the parametric plane where the period Px has imaginary values (i.e. the condition of the horizontal instability of the prominence) when accounting for conditions (2) and (3), are shown in Fig. 4, and are expressed as 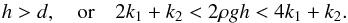 (14)
(14)
5. Discussion and conclusions
The developed model provides a simple, analytical treatment of global transverse oscillations and mechanical stability of quiescent prominences. In this paper, the term “global” denotes the collective nature of the considered oscillation, when the prominence oscillates as a whole, in contrast to the oscillations of individual threads. The term is connected with the observational manifestation of the considered oscillation, rather than a specific interpretation, for example a fundamental longitudinal harmonic of a kink or sausage oscillation. Properties of the oscillations are determined by the value of the electric current in the prominence, its density and height above the photosphere, and the parameters of the magnetic dip caused by external magnetic sources. As mentioned above, in the linear regime considered in this study, the vertically and horizontally polarised oscillations are essentially decoupled, and the obliquely or elliptically polarised oscillations can be represented as a linear superposition of separate vertical and horizontal modes. Furthermore, the stability conditions in both the z- and x-directions given in Eqs. (10) and (14) do not interfere with each other, and the oscillation periods given by expressions (9) and (13) in both directions are independent.
For the prominence current domination in the considered magnetic system (I/i< 1), the prominence displacements in both vertical and horizontal directions are found to be stable (cf. van den Oord et al. 1998) when the prominence’s height h above the photosphere is less than the half-distance d between the photospheric current sources configuring the dip (see Fig. 4). In the case when the external currents dominate (I/i> 1), the prominence is stable only in the narrow regions of parameters, determined by conditions (10) and (14). These analytical findings agree with numerous observational results describing the prominence instability occurring when its height h reaches a critical value (see e.g. Vršnak 2008).
Exact analytical dependences of the periods of the prominence oscillations upon the parameters of the system derived in Eqs. (9) and (13) allow for seismological diagnostics of the current in the prominence. For example, taking a typical value of PKR ≈ 20 min (Kuperus & Raadu 1974) and fixing h = 0.6 d, for the observed periods of the vertical transverse oscillations, Pz ≈ 80 min (Bocchialini et al. 2011), the prominence current i with respect to the photospheric current I, according to Eq. (9), can be estimated as I ≈ 0.94 i. Using the ratio I/i and the geometrical parameters h and d of the model, it is possible to estimate the coronal magnetic field at the prominence’s equilibrium position, which is caused by the external photospheric sources, I as 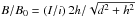 , where B0 is the magnetic field caused by the interaction of the prominence current i with the conductive photosphere used in the KR model in the absence of external magnetic sources. In addition, the developed model can also be used for the numerical modelling of the excitation of prominence oscillations (e.g. Takahashi et al. 2015).
, where B0 is the magnetic field caused by the interaction of the prominence current i with the conductive photosphere used in the KR model in the absence of external magnetic sources. In addition, the developed model can also be used for the numerical modelling of the excitation of prominence oscillations (e.g. Takahashi et al. 2015).
The proposed model developed within the line currents concept also has a number of shortcomings. In fact, we neglect the effects of the magnetic field curvature and the finite wave number of the perturbations in the direction along the current, which are important, for example, for kink oscillations of coronal loops and prominence threads (e.g. Edwin & Roberts 1983; Joarder et al. 1997). They add the additional restoring force that may decrease the oscillation period. We also do not consider thermodynamical effects affecting the prominence development itself (e.g. Kuin & Martens 1982). In addition, in our model the electric currents are considered to be linear, i.e. wire-like. However, there may be important effects connected with the spatial distribution of the current in the plane of the oscillation. For example, in a more general model, a prominence could possibly be considered as a vertical current sheet. In that case the parameters of the modes of oscillations may become dependent on height, which may be relevant to the interpretation of some of the observational findings (e.g. Hershaw et al. 2011). However, a further discussion of this issue would be beyond the scope of this paper. Another important limitation of this study is that we consider only small-amplitude oscillations and do not account for the effects of large amplitudes that are observed (see e.g. Tripathi et al. 2009). Accounting for these effects will be the aim of a future study.
Acknowledgments
This work was supported by the European Research Council under the project No. 321141 SeismoSun, the STFC consolidated grant ST/L000733/1, and the BK21 plus program of the National Research Foundation funded by the Ministry of Education of Korea.
References
- Anzer, U. 2009, A&A, 497, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Oliver, R., & Ballester, J. L. 2012, Liv. Rev. Sol. Phys., 9, 2 [Google Scholar]
- Asai, A., Ishii, T. T., Isobe, H., et al. 2012, ApJ, 745, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Bashkirtsev, V. S., & Mashnich, G. P. 1993, A&A, 279, 610 [NASA ADS] [Google Scholar]
- Bocchialini, K., Baudin, F., Koutchmy, S., Pouget, G., & Solomon, J. 2011, A&A, 533, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cargill, P. J., Chen, J., & Garren, D. A. 1994, ApJ, 423, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Filippov, B. 2016, MNRAS, 455, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Filippov, B. P., Gopalswamy, N., & Lozhechkin, A. V. 2001, Sol. Phys., 203, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Hershaw, J., Foullon, C., Nakariakov, V. M., & Verwichte, E. 2011, A&A, 531, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isobe, H., & Tripathi, D. 2006, A&A, 449, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joarder, P. S., & Roberts, B. 1993, A&A, 277, 225 [NASA ADS] [Google Scholar]
- Joarder, P. S., Nakariakov, V. M., & Roberts, B. 1997, Sol. Phys., 173, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S., Nakariakov, V. M., & Cho, K.-S. 2014, ApJ, 797, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Schlüter, A. 1957, Z. Astrophys., 43, 36 [Google Scholar]
- Kleczek, J., & Kuperus, M. 1969, Sol. Phys., 6, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Kuin, N. P. M., & Martens, P. C. H. 1982, A&A, 108, L1 [NASA ADS] [Google Scholar]
- Kuperus, M., & Raadu, M. A. 1974, A&A, 31, 189 [NASA ADS] [Google Scholar]
- Luna, M., & Karpen, J. 2012, ApJ, 750, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, M., Terradas, J., Khomenko, E., Collados, M., & de Vicente, A. 2016, ApJ, 817, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Mashnich, G. P., & Bashkirtsev, V. S. 1990, A&A, 235, 428 [NASA ADS] [Google Scholar]
- Molowny-Horas, R., Oliver, R., Ballester, J. L., & Baudin, F. 1997, Sol. Phys., 172, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., & Ballester, J. L. 2002, Sol. Phys., 206, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R., Ballester, J. L., Hood, A. W., & Priest, E. R. 1993, ApJ, 409, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Ichimoto, K., Ishii, T. T., et al. 2014a, ApJ, 786, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y. D., Chen, P. F., & Ichimoto, K. 2014b, ApJ, 795, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Asai, A., & Shibata, K. 2015, ApJ, 801, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Soler, R., Díaz, A. J., Oliver, R., & Ballester, J. L. 2013, ApJ, 778, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, D., Isobe, H., & Jain, R. 2009, Space Sci. Rev., 149, 283 [NASA ADS] [CrossRef] [Google Scholar]
- van den Oord, G. H. J., Schutgens, N. A. J., & Kuperus, M. 1998, A&A, 339, 225 [NASA ADS] [Google Scholar]
- Vršnak, B. 2008, Ann. Geophys., 26, 3089 [Google Scholar]
All Figures
 |
Fig. 1 Massive prominence with a line current i located at the height h above the photosphere in the magnetic dip configured by two photospheric currents I, with d being the half-distance between the currents. The mirror current i generated by the conductive properties of the photosphere is located strictly below the prominence. The field lines of the total magnetic field produced by the photospheric, mirror, and prominence sources are shown for h = 0.5 d and i = 0.5 I. |
| In the text | |
 |
Fig. 2 Magnetic force FL (2) acting upwards on the unperturbed prominence for different values of the prominence i and photospheric I currents. The horizontal dotted line shows a constant gravity force ρg needed to satisfy equilibrium condition (2). This example shows that the system may have up to three different equilibria (blue asterisks) depending upon the values of the parameters of the model. |
| In the text | |
 |
Fig. 3 Left: period Pz (9) of vertical oscillations of a prominence vs. the currents ratio I/i for different values of the dimensionless parameter a = 2ρgh/k2. We note that the case a = 1 corresponds to the KR limit (Kuperus & Raadu 1974) when the effect of the photospheric currents is negligibly small. Right: period Px (13) of horizontal oscillations depending upon the same parameters I/i and a as shown in the left panel. Dashed lines in both panels show a threshold values of I/i where periods (9) and (13) become imaginary, and corresponding instabilities develop. |
| In the text | |
 |
Fig. 4 Parametric regions of the prominence instability, determined by equilibrium condition (3), (10) (vertical instability), (14) (horizontal instability). Left and right panels show the corresponding regions determined via ρ and h, and h and d, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


