| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526512 | |
| Published online | 08 September 2015 | |
Online material
Appendix A: Validity of ideal plasma assumption
 |
Fig. A.1
Plasma coupling parameter Γ as a function of Rosseland mean optical depth τR. Gray area marks the regime of (strong) coupling where our original assumption of ideal gas law slowly breaks. Presented are coupling parameters for atmosphere compositions of pure iron (red lines) and solar mixture of H and He with metallicity Z = 1 Z⊙ (SolA1, black lines) and Z = 40 Z⊙ (SolA40, blue lines) computed for hydrogen (solid lines), carbon (dashed) and iron (dot-dashed) ions. |
| Open with DEXTER | |
Compared to previous atmosphere models computed with hydrogen or helium compositions our work differs substantially due to high number densities of metals producing large electron number densities. In the very deep layers, the dense plasma might become strongly coupled invalidating our assumption of ideal gas law (17). To quantify the depth where the coupling starts to be important, we can compare the ion specific Coulomb energies EC and local thermal energies ETh to get the so-called plasma coupling parameter, which is defined as 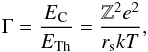 (A.1)
(A.1)
where ![]() is the Wigner-Seitz radius, i.e. the typical inter-particle distance, Z is the charge of the ion and ne is the local electron density (see e.g. Chen 1984, for basic plasma parameters). For an ideal plasma (with equation of state that of the ideal gas), the thermal (kinetic) energy of ions is larger than the interaction potentials. This corresponds to the situation Γ ≪ 1. In the opposite regime, pair distribution of ions becomes strongly localized and the plasma starts to crystallize into an (ideal) solid state. Between these two states there exists a mixed phase of fluid-like plasma around Γ ~ 1. The area where our approach is valid is limited to the case of the weakly coupled plasma, Γ ≪ 1.
is the Wigner-Seitz radius, i.e. the typical inter-particle distance, Z is the charge of the ion and ne is the local electron density (see e.g. Chen 1984, for basic plasma parameters). For an ideal plasma (with equation of state that of the ideal gas), the thermal (kinetic) energy of ions is larger than the interaction potentials. This corresponds to the situation Γ ≪ 1. In the opposite regime, pair distribution of ions becomes strongly localized and the plasma starts to crystallize into an (ideal) solid state. Between these two states there exists a mixed phase of fluid-like plasma around Γ ~ 1. The area where our approach is valid is limited to the case of the weakly coupled plasma, Γ ≪ 1.
The Γ-values are presented in Fig. A.1 for different compositions and ions. The regime of intermediate coupling Γ ~ 1 is reached only for heavier ions in the electron-rich dense layers at Rosseland optical depths ≳104. Thus this cannot affect the emergent spectra. However, this can cause problems if the maximum column depth mmax is chosen to be too large so that the regime Γ ≳ 1 is reached within our computational domain. In these very deep layers the inter-particle effects may become substantial, leading to a numerically challenging instability between the strong (and unphysical) recombination via the Saha equation and forced ionization because of the occupation probability formalism used. This is a known problem because Saha’s model assumes ideal gas conditions (i.e. every effect of the plasma is asserted on its ions and atoms internal structures) and uses only the ground state configurations in the ionization balance equations (Rogers et al. 1996). It is also worth mentioning that the pressure ionization method used here is a more of a phenomenological correction scheme as its corrections to non-ideal effects are obtained by minimizing a free energy of predefined gas (Hummer & Mihalas 1988). More fundamental and physical approach would be the (activity) expansion of the grand canonical partition function of the plasma where pressure ionization is a consequence of the theory (see e.g. Rogers et al. 1996). Such a fundamental treatment of plasma is, however, extremely challenging and out of the scope of this paper.
Appendix B: Color correction tables
Color correction and dilution factors from the blackbody fits.
© ESO, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


