| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323332 | |
| Published online | 16 April 2014 | |
Online material
Appendix A: List of LMXB and HMXB sources used in the calculations
Full list of sources used in the calculations with the corresponding data (also available at http://www.mpa-garching.mpg.de/~molaro).
List of sources used in the calculations, ranked by 2−10 keV luminosity.
Appendix B: Contribution of Sgr A∗
As discussed in Sect. 2, the past activity of the currently low quiescent source Sgr A∗ might have significantly contributed to the cumulative X-ray output of the Galaxy, and hence to the diffuse GRXE component. In Fig. B.1 we show the minimum luminosity required for the flux from this source to outshine the contribution of the entire XBs population at different positions on the Galactic plane, estimated as 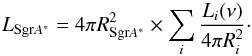 (B.1)
(B.1)
 |
Fig. B.1
Minimum Sgr A∗ luminosity required for the source’s flux to be higher than the total HMXBs (left panel) and LMXBs (right panel) contribution at different positions on the Galactic plane. If we know the star formation rate and the mass of a galaxy, we can estimate the X-ray luminosity contributed by the X-ray binaries and similarly find when the AGNs contribute more than the X-ray binaries to the heating of the gas in other galaxies with AGNs. |
| Open with DEXTER | |
Appendix C: Scattering cross-sections
In Fig. C.1 we illustrate the energy dependence of the scattering cross-section for the case of H2 scattering. In Figs. C.2 and C.3 we highlight the additional effects caused by bound electrons by showing the ratio of contributions from H2 and He with respect to the free electrons. The energy dependence of Rayleigh scattering is clearly evident. At high energies, Rayleigh scattering operates only on a very narrow range of scattering angles and the total scattering cross-section approaches the Klein-Nishina cross-section. At low energies, coherent Rayleigh scattering results in the enhancement of the cross section for a significant range of scattering angles, resulting in a higher average scattering rate of low-energy photons. The average scattered spectrum is therefore softer than the average incident spectrum. The contribution of molecular hydrogen as well as helium and heavier elements is compared in Table C.1 in the Rayleigh scattering limit (0° scattering angle). The elements heavier than helium contribute ≲10% in this extreme case, and the actual contribution when suitably averaged over different scattering angles would be smaller than the values in the table.
 |
Fig. C.1
Cross-section (Rayleigh+ Compton) in polar coordinates, σ(θ)eiθ, where σ is the amplitude of the cross-section in units of |
| Open with DEXTER | |
Near the Galactic center, a luminosity of ≳1037 erg/s from Sgr A∗ would be enough to become comparable with the illumination from X-ray binaries. On the outskirts of the Galaxy, on the other hand, Sgr A∗, or some other ultra-luminous source near the Galactic center, can be ignored as long as its luminosity is ≲1039−1040 erg/s.
 |
Fig. C.2
Ratio of the Rayleigh + Compton differential cross-section of H2 + He to HI + He (where each element is weighted by relative abundance) as a function of energy for different scattering angles. The total cross section approaches that of unbound electrons as the importance of coherence effects decreases with energy, because of the suppression of Rayleigh scattering. |
| Open with DEXTER | |
Elements according to maximal contribution to Rayleigh scattering if all hydrogen is in atomic form (or molecular form, given in parentheses).
 |
Fig. C.3
Ratio of intensity from the Monte Carlo simulated HMXBs (left column) and LMXBs (right column) scattered along the Galactic plane (b = 0) by H2 (top row) and He (bottom row) to the intensity that would be scattered if all electrons were unbound. The range of scattering angles over which the Rayleigh scattering dominates the scattering cross section depends on the characteristic size of the electron distribution in the atom or molecule, which differs for different elements and molecules (see Sect. 4.1). This leads to a nonlinear dependence of the ratio of cross sections for different elements and molecules on the scattering angle. At each longitude many different scattering angles contribute, corresponding to the relative position of the X-ray sources w.r.t. the gas along the line of sight, resulting in the apparent longitudinal dependence of the ratio profiles. |
| Open with DEXTER | |
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.