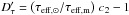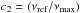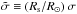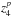| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 12 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220817 | |
| Published online | 01 November 2013 | |
Online material
Appendix A: Can we distinguish the dependence on ℳa?
We have seen that the new theoretical scaling relations for τeff and σ are – on a global scale – aligned with the Kepler measurements. However, the question we address here is whether or not the observations allow one to quantitatively confirm the dependence of the new scaling relations on ℳa. To this end we compare the new scaling relations with the classical ones.
Appendix A.1: Characteristic time-scale, τeff
To check the dependence of the new theoretical scaling relation for τeff on ℳa, we computed the relative differences between the new scaling relation and the measurements as well as the relative differences between the classical theoretical scaling relation 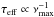 and the measurements. In practice, we computed the quantities Dτ = (τeff, ⊙/τeff,m) z2 − 1 and
and the measurements. In practice, we computed the quantities Dτ = (τeff, ⊙/τeff,m) z2 − 1 and 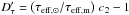 , where τeff,m is the measured value of τeff, τeff, ⊙ = 230 s is the adopted solar reference (Michel et al. 2008),
, where τeff,m is the measured value of τeff, τeff, ⊙ = 230 s is the adopted solar reference (Michel et al. 2008), 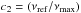 , and z2 is the new scaling relation (Eq. (18)). We considered in our comparison only the sample of MS and sub-giant stars because they are better indicator for the dependence on ℳa.
, and z2 is the new scaling relation (Eq. (18)). We considered in our comparison only the sample of MS and sub-giant stars because they are better indicator for the dependence on ℳa.
The histograms of Dτ and 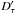 are shown in Fig. A.1 (top panel). The median value and the standard deviation of Dτ are − 10% and 12%, respectively, while for
are shown in Fig. A.1 (top panel). The median value and the standard deviation of Dτ are − 10% and 12%, respectively, while for 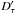 they are equal to 15% and 14%, respectively.
they are equal to 15% and 14%, respectively.
For both scaling relations, the dispersion and deviation from the measurements can in part arise because we observed an heterogeneous population of stars, in particular stars with different metal abundance. Indeed, ℳa is expected to depend on the surface metal abundance (see e.g. Houdek et al. 1999; Samadi et al. 2010b,a). However, we would have expected a higher dispersion for Dτ than for 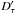 . Indeed, the new scaling relation depends on ℳa and, according to Eq. (17), the Mach number ℳa strongly depends on Teff and more weakly on g. Therefore, the uncertainties associated with Teff and log g introduce a spread in the determination of z2, and subsequently on Dτ.
. Indeed, the new scaling relation depends on ℳa and, according to Eq. (17), the Mach number ℳa strongly depends on Teff and more weakly on g. Therefore, the uncertainties associated with Teff and log g introduce a spread in the determination of z2, and subsequently on Dτ.
Teff is based on photometric indices and is measured with an rms precision of about 100 K (see Molenda-Żakowicz et al. 2010; Bruntt et al. 2011, 2012; Thygesen et al. 2012), while log g is obtained from seismology with a typical rms precision of 0.1 dex (Bruntt et al. 2012; Morel & Miglio 2012). The rms errors in Teff and log g introduce a relative dispersion in z2 of the order of 6% for a typical RG star with Teff = 4500 K and log g = 2.3, and about 5% for a typical MS with Teff = 6000 K and log g = 4 (these typical relative dispersions are shown in Fig. 4).
The median deviation of the new theoretical scaling relation from the measurements is found to be of the same order as that of the classical relation. However, the difference between the median of Dτ and of 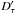 remains within the dispersion of Dτ. Therefore, we cannot distinguish the new scaling relation from the classical one. Finally, the mean deviation of the new scaling relation from the measurements is about two times lower than its associated dispersion. We therefore conclude that, as the classical scaling relation, the new one is compatible with the observations, but we cannot firmly confirm its dependence with ℳa.
remains within the dispersion of Dτ. Therefore, we cannot distinguish the new scaling relation from the classical one. Finally, the mean deviation of the new scaling relation from the measurements is about two times lower than its associated dispersion. We therefore conclude that, as the classical scaling relation, the new one is compatible with the observations, but we cannot firmly confirm its dependence with ℳa.
 |
Fig. A.1
Top: histogram of the relative differences (in %) between the theoretical τeff and the measured ones. The solid black line corresponds to the histogram of the relative difference Dτ = (τeff, ⊙/τeff,m) z2 − 1 and the dashed red line to residuals |
| Open with DEXTER | |
Appendix A.2: Brightness fluctuations, σ
In the same way as for τeff, we checked the dependence on ℳa of the new scaling relation for σ by computing the relative difference between the new theoretical scaling relation (Eq. (19)) and the measurements as well as the relative difference between the classical theoretical scaling relation 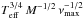 (Kjeldsen & Bedding 2011; Mathur et al. 2011) and the measurements. In practice, we computed the quantities Dσ = (σ⊙/σm) z3 − 1 and
(Kjeldsen & Bedding 2011; Mathur et al. 2011) and the measurements. In practice, we computed the quantities Dσ = (σ⊙/σm) z3 − 1 and 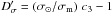 , where σm is the measured value of c2 ∝ σ, σ⊙ = 43 ppm is the adopted bolometric amplitude measured for the Sun (Michel et al. 2008), and c3 is given by Eq. (20), where the term (Teff/Teff, ⊙)3/4 (M⊙/M)1/2 is evaluated according to Eq. (22). Like for τeff, we considered only MS and sub-giant stars because they are the better indicators.
, where σm is the measured value of c2 ∝ σ, σ⊙ = 43 ppm is the adopted bolometric amplitude measured for the Sun (Michel et al. 2008), and c3 is given by Eq. (20), where the term (Teff/Teff, ⊙)3/4 (M⊙/M)1/2 is evaluated according to Eq. (22). Like for τeff, we considered only MS and sub-giant stars because they are the better indicators.
We have plotted in Fig. A.1 (bottom panel) the histograms associated with Dσ and 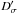 . The median value and standard deviation of Dσ are 46% and 42%, respectively, while for
. The median value and standard deviation of Dσ are 46% and 42%, respectively, while for 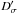 they are equal to −12% and 17%, respectively.
they are equal to −12% and 17%, respectively.
As mentioned for the scaling of τeff (see Sect. 6.1), for both scaling relations, the dispersion and deviation with the measurements can in part arise from the fact that we observed an inhomogeneous sample of stars, in particular, stars with a different surface metal abundances. Indeed, the amplitude of the granulation background is expected to depend on the surface metal abundance (for a particular low-metal F-type star see Ludwig et al. 2009a). Furthermore, for the new scaling relation an rms error of 100 K in Teff and a rms error 0.1 dex on log g results for z3 in a typical error about 12% for RG stars and about 10% for a typical MS (these typical relative dispersions are shown in Fig. 5). On the other hand, the uncertainties associated with Teff have no direct impact on the classical scaling relation given by Eq. (20) since the term 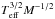 is estimated using only seismic constraints (see Eq. (22)).
is estimated using only seismic constraints (see Eq. (22)).
Compared with the new scaling relation, the classical one results in a smaller difference with the observations. However, the deviations of the two scaling relations from the measurements are found to depend on Teff. The highest deviations are obtained for the F-dwarf stars (Teff = 6000 − 7500 K, see Fig. 6 and Sect. 7). As discussed in Sect. 7, this is very likely a consequence of the lack of modelling of the impact of magnetic activity on the granulation background.
As stressed in Paper I, our theoretical calculations are expected to be valid for stars with a low level of activity. If we exclude the F-dwarf stars from our sample, the median deviation of the new scaling relation w.r.t the measurements is −2% (±30%), while for the classical scaling relation it is equal to −19% (±18%). In that case, the new scaling relation results in a lower deviation. However, the difference between the median value of Dσ and this of 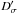 is smaller than the standard deviation of Dσ. Therefore, it is not possible to distinguish the new theoretical scaling relation from the classical one.
is smaller than the standard deviation of Dσ. Therefore, it is not possible to distinguish the new theoretical scaling relation from the classical one.
In conclusion, as the classical scaling relation, our theoretical scaling relation is compatible with the observations, but we cannot confirm the dependence on ℳa. Observations of K-dwarf stars (Teff = 3500 − 5000 K) could in principle help to check the dependence of the theoretical scaling relation on ℳa. Indeed, for instance the 3D model with Teff ≃ 4500 K and log g = 4.0 (K dwarf) has νmax = 1.3 mHz ℳa ≃ 0.18, and σ ≃ 18 ppm, while the 3D model Teff ≃ 5900 K and same log g (G dwarf) has νmax = 1.1 mHz ℳa ≃ 0.31, and σ ≃ 110 ppm. The relative difference in σ between the K dwarf model and the G-dwarf model is 84%. This is much higher than the dispersion in Dσ and 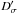 .
.
Appendix B: Removing the degeneracy with the mass and the radius
As seen in Sect. 4.4, the individual theoretical values of σ are found to scale as 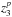 with the slope p = 1.10. As we will show now, the deviation of the individual values of σ from a linear scaling with z3 is for a large part due to the considerable degeneracy that occurs for red giants between M and R. Indeed, the theoretical values of σ scale as
with the slope p = 1.10. As we will show now, the deviation of the individual values of σ from a linear scaling with z3 is for a large part due to the considerable degeneracy that occurs for red giants between M and R. Indeed, the theoretical values of σ scale as 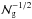 , and hence as the stellar radius Rs (see Eqs. (4) and (7)). Furthermore, z3 scales as M− 1/2. Therefore theoretical values of σ and z3 directly depend on the masses and radii attributed to the 3D models. However, two red giants with same Teff and log g can have very different values
, and hence as the stellar radius Rs (see Eqs. (4) and (7)). Furthermore, z3 scales as M− 1/2. Therefore theoretical values of σ and z3 directly depend on the masses and radii attributed to the 3D models. However, two red giants with same Teff and log g can have very different values
of R and M. Furthermore, the masses and radii attributed to our 3D models were obtained from a grid of standard stellar models with fixed physical assumptions, and all of these models are in the pre-helium-burning phase, which is not the case for all observed RG stars.
When we multiply theoretical σ by Rs/R⊙, we obtain a quantity that does no longer depend on the radius attributed to the 3D model. Furthermore, the quantity z4 ≡ z3 (Rs/R⊙) scales as g− 1/2. As a consequence, z4 does not depend on the mass attributed to the 3D model. To remove possible bias introduced by the determination of the masses and radii of the 3D models we must therefore compare theoretical values of 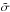 as a function of z4 with the measurements multiplied by the star radii. To do this, we need to determine the radii of the observed targets. Combining the scaling relation for νmax with the one for Δν gives (see e.g. Stello et al. 2009; Kallinger et al. 2010; Mosser et al. 2010)
as a function of z4 with the measurements multiplied by the star radii. To do this, we need to determine the radii of the observed targets. Combining the scaling relation for νmax with the one for Δν gives (see e.g. Stello et al. 2009; Kallinger et al. 2010; Mosser et al. 2010) 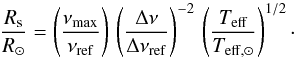 (B.1)Multiplying Eq. (19) by Eq. (B.1) gives the scaling relation for
(B.1)Multiplying Eq. (19) by Eq. (B.1) gives the scaling relation for 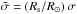 with the help of Eq. (22)
with the help of Eq. (22) 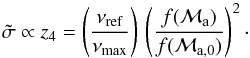 (B.2)To compare theoretical
(B.2)To compare theoretical 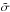 with the measurements, we multiply the measured σ by the ratio Rs/R⊙ given by Eq. (B.1). We have plotted theoretical and measured values of
with the measurements, we multiply the measured σ by the ratio Rs/R⊙ given by Eq. (B.1). We have plotted theoretical and measured values of 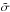 in Fig. B.1. The individual theoretical values of
in Fig. B.1. The individual theoretical values of 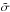 are found to scale as
are found to scale as 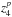 with p = 1.03 and are therefore better aligned with the measurements than those of σ.
with p = 1.03 and are therefore better aligned with the measurements than those of σ.
 |
Fig. B.1
|
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.