| Issue |
A&A
Volume 559, November 2013
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201219846 | |
| Published online | 29 October 2013 | |
Online material
Appendix A: Testing the method of extinction correction for the star counts
In Sect. 3.1, we have proposed a simple algorithm to correct the Ks-band star counts from extinction, in which we only need the observed magnitudes in J and Ks. There is some discussion of the method in the literature (e.g., Alard 2001; López-Corredoira et al. 2001) or a similar method for redder wavelengths (e.g., M11), and the logic is clear: the average reddening is proportional to the extinction, thus the average (J − Ks) gives us information about the average extinction along the line of sight. In our case, looking at the central regions (|ℓ|≤ 20°, |b|< 2.5°) and excluding the sources with (J − Ks) < 0.5, the contribution of disk sources is low. So, star counts are dominated by sources from the long bar or bulge+long bar. Since these structures have low dispersion of distances, the dispersion of extinction of the sources will not be high; as a result the application of the method of correction will recover more or less the average counts up to a limiting magnitude. In this section, we carry out some simulations to show that the method of correction approximately recovers the equivalent counts if we have no extinction.
For our simulation, we take a model of the Galaxy with a stellar density of a disk from López-Corredoira et al. (2004), a bulge from López-Corredoira et al. (2005, model 2), and a long bar from LC07. Spiral arms and halo contributions are negligible so we do not include them here. In Fig. A.1, we plot the face-on image of the Galaxy according to this model. It is not important here whether this is a true representation of the Galaxy or not. At present, it is just a density distribution to test our method of extinction correction.
We use a model of populations from Wainscoat et al. (1992) to characterize the distribution of magnitudes and colors in each point of the space. We take the disk populations, since the differences with the older population of the bulge only affects very bright giants or supergiants (López-Corredoira et al. 2005), which are brighter than our range of magnitudes. The long bar is supposed to be an intermediate population, so again a distribution of populations like the disk is appropriate. Nonetheless, we insist that this is just a toy model for evaluating the method of extinction correction, so variations in this assumption are not important here. With the mentioned density distribution and the population distribution, we integrate along the line of sight (there is a factor r2 in the integration), and we get the synthetic color–magnitude diagram of Fig. A.2 (left) at ℓ = −10°, b = 1°. We introduce a toy model of extinction. We assume a distribution of dust as 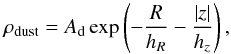 (A.1)
(A.1)
where hR = 3 kpc, hz = 0.1 kpc, and extinction in Ks in the solar neighborhood of 0.07 mag/kpc, which gives 2.8 mag of extinction up to the center of the Galaxy at distance 8.0 kpc. Again, whether this distribution of dust is exact or not is not important for our exercise. In Fig. A.2 (right) we plot the same color–magnitude diagram as before but introducing this extinction, assuming 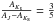 (see 5th paragraph of Sect. 3.1).
(see 5th paragraph of Sect. 3.1).
Now, we calculate the star counts with (J − Ks) ≥ 0.5 without extinction in Fig. A.2 (left) and with extinction (Fig. A.2. right) applying the correction of Eq. (A.1) with (J − Ks)0 = 1.0. The results are plotted in Fig. A.3, for three different lines of sight with three different total extinctions up to the semiaxis of the long bar: respectively 2.78 mag up to a distance of 8 kpc for ℓ = 0, b = 0; 1.24 mag up to at distance 9.7 kpc for ℓ = −10°, b = 1°; 0.47 mag up to a distance 12.9 kpc for ℓ = −20°, b = 2°. We therefore test different longitudes, latitudes, and extinctions.
As we can see in Fig. A.3, the method approximately recovers the counts that would be produced without extinction, within small errors typically of 5–10%, which are not important for our purposes. The variation of 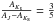 will also introduce some extra error.
will also introduce some extra error.
 |
Fig. A.1
Face-on view (in units of kpc) of the Model of the Galaxy (see text in Appendix A) used to test the extinction correction method. |
| Open with DEXTER | |
 |
Fig. A.2
Synthetic color–magnitude diagram in the direction ℓ = −10°, b = 1° (left) without extinction; (right) with extinction. |
| Open with DEXTER | |
 |
Fig. A.3
Calculations of the counts (arbitrary normalization) for the model in different regions without extinction, and with extinction+correction of the extinction. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


