| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 25 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201220189 | |
| Published online | 26 September 2013 | |
Online material
Appendix A: Effect of different model realizations
 |
Fig. A.1
Comparison between different model realizations. See text. |
| Open with DEXTER | |
As described in Sect. 2, we downscaled our simulated disk by a factor of f = 1.67, to place the bar’s OLR just inside the solar circle, at ~7.5 kpc (assuming the Sun is at 8 kpc), in agreement with its expected effect on the local disk dynamics (e.g., Dehnen 2000; Minchev et al. 2010).
We now would like to see how our results change when we rescale the disk by a different factor. We used f = 1.4, which places the solar radius ~1.25 kpc inward of the standard location used in the paper. This is equivalent to having a stronger (longer) bar. We refer to this realization as model A.
As a second test, we started the implementation with chemistry 2.7 Gyr later, thus avoiding the early-on massive mergers. We integrated the simulation for additional 2.7 Gyr so that we, again, have 11.2 Gyr of evolution. To keep the correct location with respect to the bar’s resonances, we downscaled the disk radius by f = 2.1 to account for the bar’s slowing down. This realization is referred to as model B.
Note that in the two cases above we only changed the dynamics but not the input chemistry, i.e., we resampled the SFH according to our chemical model, with the 8 kpc chemistry assigned to the rescaled 8 kpc radius in the simulation, etc.The results are shown in Fig. A.1, where in the first two rows we compare the birth-radius and metallicity distributions resulting from our new realizations model A (left) and model B (right), with our standard model (middle). As expected, when the solar radius is shifted closer to the bar (model A), for all age-bins larger fractions of stars arrive from inside the bar’s CR (dotted-red vertical line in the top row); to see this more easily, we overlaid the original total histogram (in pink) in the left and right panels.
Inspecting the metallicity distributions in the second row of Fig. A.1, we see a shift in the peak of less than 0.1 dex to negative values when the Sun is closer to the bar. However, the changes are not drastic and the rest of the results in the paper are not affected much by this change. Whether this is true for the entire disk will be investigated in Paper II.
As became evident in the discussion of the age-metallicity relation (Sect. 5.3), in our simulation we have a deficiency of stars with ages >~9.5 Gyr at r > 10 kpc for our standard model. However, this is a very small fraction of particles, as can be inferred from the bottom-right panel of Fig. 2 (the SFRs at these times and radii attain a maximum at ~2 M⊙ pc-2 Gyr-1 for r = 10 kpc, sharply decreasing for older stars and larger radii). By shifting the solar radius inward, this artifact is now lost. That this is indeed a very small fraction can be seen by comparing the right tails of the oldest r0-distributions (red histograms) in the first row, left and middle panels.
The right column of Fig. A.1 shows model B, where we avoided the early-on massive mergers phase, but kept the bar resonances at the same distances from the Sun. A smaller number of stars arrives from inside the bar’s CR in this case, than in our standard model (see overlaid pink line). This results mostly from the lack of the strong peak in the r0-distribution of the oldest stars (red line). We showed in Sect. 6.5 that the enhancement in the peak at r0 ~ 3 kpc is due to the massive mergers, which we avoided here.
In the bottom-left and right panels of Fig. A.1 we compare the vertical velocity dispersion, σz(r) (black solid), and the mean rotational velocity, Vφ(r) (blue dashed), radial profiles resulting from the new realizations with our standard model (corresponding pink curves). Model A results in a slightly larger σz throughout (left). The difference between the standard model and model B is much more striking (right). Most importantly, the oldest stars in model B have σz about a factor of two smaller than when massive mergers are present. The highest radial velocity dispersion for the oldest stars (not shown) also drops form ~65 to ~45 km s-1, which is reflected in the higher Vφ-values. The lower velocity dispersions and rotational velocity difference between young and old stars is unlike the observations in the solar neighborhood. We can therefore argue that the MW thick disk is unlikely to have been formed through a quiescent disk evolution. An observational test must be devised to ascertain this possibility.
Appendix B: The chemical evolution model adopted in this work
We adopted a pure thin-disk chemical model (i.e., not the two-infall model of Chiappini et al. 1997), forming by continuous gas accretion (an exponential function of time – see Eq. (B.1)). The galactic disk was divided into two-kpc-wide concentric rings that evolve independently without exchange of gas. We did not take into account radial gas flows or SN-driven winds (see Sect. 4). Most of the observational constraints are confined to the solar vicinity (as summarized in Table B.1).
Main observational constraints for the solar neighborhood.
An inside-out formation of the disk (in the sense of a more intense SFR in the inner regions – see Fig. 2, middle panel) was simulated via a radial dependency of the gas accretion timescale (assumed linear for simplification), as follows 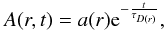 (B.1)where A(r,t) is the gas infall rate and τD(r) is the timescale for the infalling gas onto the disk, given by (as in Chiappini et al. 2001)
(B.1)where A(r,t) is the gas infall rate and τD(r) is the timescale for the infalling gas onto the disk, given by (as in Chiappini et al. 2001) 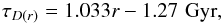 (B.2)for galactocentric distances r ≥ 2 kpc.
(B.2)for galactocentric distances r ≥ 2 kpc.
The coefficient a(r) in Eq. (B.1) was chosen such as to reproduce the observed current total surface mass density in the thin disk as a function of the galactocentric distance given by 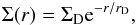 (B.3)where ΣD is such that a total mass density of ~50 M⊙ pc-2 is reached at the solar galactocentric distance (taken as 8 kpc), for a disk with a scale length rD = 3 kpc (as shown in Fig. 2, upper-left panel).
(B.3)where ΣD is such that a total mass density of ~50 M⊙ pc-2 is reached at the solar galactocentric distance (taken as 8 kpc), for a disk with a scale length rD = 3 kpc (as shown in Fig. 2, upper-left panel).
The SFR adopted here has the same formulation as in Chiappini et al. (1997): 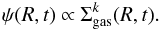 (B.4)The two free parameters are the gas surface density exponent (here taken as equal to 1.5) and the star formation efficiency, which we assumed is dependent on the total surface density as in Chiappini et al. (1997).
(B.4)The two free parameters are the gas surface density exponent (here taken as equal to 1.5) and the star formation efficiency, which we assumed is dependent on the total surface density as in Chiappini et al. (1997).
We adopted the Scalo (1986) IMF, constant in time and space. The stellar lifetimes, τm, were taken from Maeder & Meynet (1989) as in our previous works. The impact of different assumptions on both IMF and stellar lifetimes on our chemical evolution results was discussed in detail in Romano et al. (2005).
Type Ia SNe are the main contributors to the iron in the disk of our MW. The timescale on which their contribution becomes important is strongly dependent on the assumed SN progenitor model. In the so-called single degenerate scenario, a C–O white dwarf (WD) in a close binary system explodes due to gas accretion from a companion in a binary system. Another proposed scenario for Type Ia SNe is the so-called double degenerate case, where two WDs merge, thus triggering the explosion (see Matteucci et al. 2009 and references therein). Matteucci et al. (2009) has recently shown that these two different SN Ia scenarios result in only negligible differences in the predicted [O/Fe] vs. [Fe/H] relation in the MW. In the present work we adopted the single degenerate scenario. The Type Ia SN rate was computed following Greggio & Renzini (1983) and Matteucci & Greggio (1986) and is expressed as (see more details in Matteucci 2001) 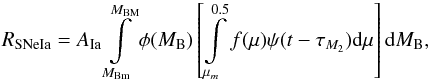 (B.5)where M2 is the mass of the secondary, MB is the total mass of the binary system, μ = M2/MB, μm = max[M2(t)/MB,(MB − 0.5 MBM)/MB], MBm = 3 M⊙, MBM = 16 M⊙. The IMF is represented by φ(MB) and refers to the total mass of the binary system for the computation of the Type Ia SN rate, f(μ) is the distribution function for the mass fraction of the secondary,
(B.5)where M2 is the mass of the secondary, MB is the total mass of the binary system, μ = M2/MB, μm = max[M2(t)/MB,(MB − 0.5 MBM)/MB], MBm = 3 M⊙, MBM = 16 M⊙. The IMF is represented by φ(MB) and refers to the total mass of the binary system for the computation of the Type Ia SN rate, f(μ) is the distribution function for the mass fraction of the secondary, 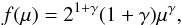 (B.6)with γ = 2; AIa is the fraction of systems in the appropriate mass range, which can give rise to Type Ia SN events. This quantity was fixed to 0.05 by reproducing the observed Type Ia SN rate at the present time (see Table B.1). Note that in the case of the Type Ia SNe the so-called production matrix is indicated with
(B.6)with γ = 2; AIa is the fraction of systems in the appropriate mass range, which can give rise to Type Ia SN events. This quantity was fixed to 0.05 by reproducing the observed Type Ia SN rate at the present time (see Table B.1). Note that in the case of the Type Ia SNe the so-called production matrix is indicated with  because of its different nucleosynthesis contribution (for details see Matteucci 2001).
because of its different nucleosynthesis contribution (for details see Matteucci 2001).
 |
Fig. B.1
Oxygen stellar yields for massive stars from Woosley & Weaver (1995). Here we adopt the solar yields (magenta circles). A stronger metallicity dependency of the oxygen yields is expected in models taking mass-loss into account (e.g., Meynet & Maeder 2002). The impact of different stellar yields is beyond the scope of the present paper and will be studied in future work. |
| Open with DEXTER | |
The equation below describes the time evolution of the gas mass fraction in the form of an element i, Gi (see Matteucci 2001): 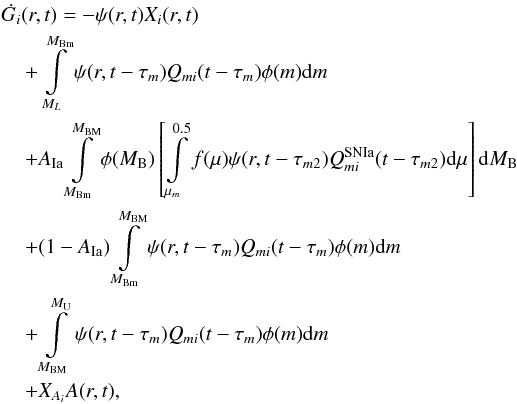 (B.7)where Gi(r,t) = [Σg(r,t)Xi(r,t)] /ΣT(r), Σg(r,t) is the surface gas density, and ΣT(r) is the present-time total surface mass density. XAi are the abundances in the infalling material, which here was taken as primordial. Xi(r,t) is the abundance by mass of the element i and Qmi indicates the fraction of mass restored by a star of mass m in form of the element i, the production matrix (see Matteucci 2001 for more details). We indicated with ML the lightest mass that contributes to the chemical enrichment and set it to 0.8 M⊙; the upper mass limit, MU, was set to 100 M⊙.
(B.7)where Gi(r,t) = [Σg(r,t)Xi(r,t)] /ΣT(r), Σg(r,t) is the surface gas density, and ΣT(r) is the present-time total surface mass density. XAi are the abundances in the infalling material, which here was taken as primordial. Xi(r,t) is the abundance by mass of the element i and Qmi indicates the fraction of mass restored by a star of mass m in form of the element i, the production matrix (see Matteucci 2001 for more details). We indicated with ML the lightest mass that contributes to the chemical enrichment and set it to 0.8 M⊙; the upper mass limit, MU, was set to 100 M⊙.
 |
Fig. B.2
Abundances of O as a function of galactocentric distance. The blue dots are the data by Andrievsky et al. (2002a,b,c, 2004). The black squares represent the mean values inside each bin and the error bars are the associated standard deviations. The red dashed line shows the prediction of our model, normalized to the mean value of the Cepheids at the galactocentric distance of the Sun. Fitting a line in the range 4 < r < 15 kpc, we estimated a gradient of ~ − 0.04 dex/kpc for the model, which matches the mean data points well. |
| Open with DEXTER | |
We adopted the stellar yields of Woosley & Weaver (1995) for the solar case, assuming no dependency on metallicity, for the contribution of massive stars. The adopted yields for oxygen are shown in Fig. B.1. As it can be seen in the figure, for the models computed by Woosley & Weaver (1995), an important difference is seen only at zero metallicities, which did not play a role in the present work (where we focused on the disk, and not the halo). In the case of iron, an important contribution comes also from Type Ia SNe. Here we adopted the stellar yields of Iwamoto et al. (1999).
Finally, in Fig. B.2 we show the resulting oxygen abundance variation with radius at the present time in our model, compared to a sample of Cepheids whose distances are well known (see Cescutti et al. 2007 and references therein). Fitting a line in the range 4 < r < 15 kpc, we estimated a gradient of ~− 0.04 dex/kpc for the model. Given the young ages of the data (~200 Myr), these are expected to trace the gas gradient in the disk today, justifying the comparison in the figure.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


