| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220351 | |
| Published online | 30 April 2013 | |
Online material
Appendix A: OIS photometric correction
Appendix A.1: OIS principle
We recall the OIS principle that consists in subtracting a reference image (R) to the current science one (I). This reference image is the best one in the time series, in the sense of sharpness and sky background level. It is then convolved to an optimal kernel which depends globally on the current science image, and locally to the position in the image (space-varying kernel). Once the reference image is convolved by the optimal kernel (K), it has the same average intensity and PSF shapes as the current science image. After subtracting the convolved reference and the science image, we obtain an image with PSF subtraction residuals, whose flux need to be measured by aperture photometry. This operation can be written as, 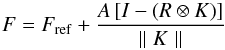 (A.1)where Fref is the flux computed on the reference image with the aperture A. With our notation, we could write Fref = A R.
(A.1)where Fref is the flux computed on the reference image with the aperture A. With our notation, we could write Fref = A R.
Appendix A.2: Choice of the aperture radius
The radii of the apertures A (which are different for each star in the reference image) depend on the intensity of the stars and on the global FWHM of all PSFs. The aperture is allowed to vary for each star so as to minimize the global photometric noise structures in the lightcurves. This is done at the expense of a photometric bias – as explained below – that can be compensated using a statistical approach detailed in the next section. The net result is a significant gain in SNR.
In order to optimize the photometric SNR, a simple method consists in selecting an aperture radius by determining all pixels with a level higher than (for example) three times the background noise. By this process, each star in the reference image has its own aperture radius A. Note that fainter stars will have smaller reference aperture radii by using this method.
These apertures will give us the reference fluxes Fref for each star, but if we use these apertures directly on the subtracted image, they will not take into account the PSF FWHM broadening (it is necessarily a broadening since the reference image is chosen as the sharpest image). A way to account for these FWHM width fluctuations is to convolve the circular reference aperture by the local kernel K. The flux is then expressed as, 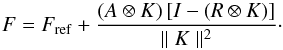 (A.2)Apart from broadening the apertures proportionally to the current science FWHM, this aperture convolution has the benefit of “apodizing” the resulting aperture, thus reducing the background noise contribution. To better understand this effect, let us consider the case of a star whose photometry is perfectly constant over time. Its reference flux is determined on a reference image with a given circular aperture radius. In another image where the PSF FWHM is larger, the star’s flux will remain the same, but will be spread-out because of degraded seeing. If we use the circular aperture convolved with the kernel K as the new aperture, we can understand why the outer pixel values (that should contribute to the true photometry) will be artificially decreased, whereas the background noise, in areas where it becomes dominant compared to the star signal, will be further attenuated.
(A.2)Apart from broadening the apertures proportionally to the current science FWHM, this aperture convolution has the benefit of “apodizing” the resulting aperture, thus reducing the background noise contribution. To better understand this effect, let us consider the case of a star whose photometry is perfectly constant over time. Its reference flux is determined on a reference image with a given circular aperture radius. In another image where the PSF FWHM is larger, the star’s flux will remain the same, but will be spread-out because of degraded seeing. If we use the circular aperture convolved with the kernel K as the new aperture, we can understand why the outer pixel values (that should contribute to the true photometry) will be artificially decreased, whereas the background noise, in areas where it becomes dominant compared to the star signal, will be further attenuated.
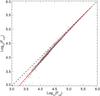 |
Fig. A.1
Plot of the reference image fluxes computed with a circular aperture (Fref) versus the same reference image computed with the kernel-convolved aperture A ⊗ K (Fcref). The fitted curve is shown in red, as well as the ideal linear trend (dashed line). |
| Open with DEXTER | |
Thus the image subtraction algorithms intrinsically and globally produces more accurate (cleaner) lightcurves than aperture photometry, but has a tendency to underestimate the photometry (and the noise level) in the case where the above-described aperture convolution procedure is used.
It should be pointed out that the photometric bias is more important for fainter stars due to the combination of two effects: firstly, as mentioned above, the associated reference image aperture radius will be smaller than for a brighter star, and secondly because the kernel size is approximately constant over the entire image. Since the average kernel size directly depends on the seeing, the photometric underestimation bias will be even stronger for fainter stars during bad seeing episodes, and can reach up to about 30% in our data.
In order to compensate for this photometric bias, we need to introduce a correction factor α such that, 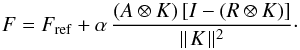 (A.3)
(A.3)
Appendix A.3: Photometric correction factor α
To assess the α factor, we simply plot the reference fluxes Fref of each star against the reference PSFs, convolved by the modified aperture, that is Fcref = (A ⊗ K) (R ⊗ K)/ ∥ K ∥ 2. This shows how the reference fluxes (in the reference image) compare to the fluxes when we use the convolved aperture A ⊗ K. If the field contains enough stars, a fitting curve can be adjusted in order to give the photometric compensation α for any measured photometric residual (Fig. A.1). The photometric correction factor α needs to be computed for every image since the optimal kernels are changing with each image. The uncertainty on α was evaluated by scrambling all the points, randomly switching them (or not) with its immediate neighbor, then performing the fit and repeating the procedure 1000 times. This test shows that α is stable at the level of about 1% up to magnitude R = 16, and raising to about 5% at R = 18. An additional test showing the robustness of the method is that the correction factor α is very well correlated with the PSF FWHM (thus consistent with the explanation given above). Although we cannot verify the exactness of the α factor for each of the stars, it appears to be an efficient first order photometric correction. Most importantly it does not introduce spurious noise structures in the lightcurves as it is the case of WASP-19 (see below).
 |
Fig. A.2
Lightcurves rms in the WASP-19 field for the aperture photometry (green dots) and for the OIS (black dots) taking into account the photometric correction described in Appendix A. The red dots correspond to the fundamental noise estimate (including photon, background and read noises). |
| Open with DEXTER | |
Appendix A.4: The case of the WASP-19 field
In the case of WASP-19, the transit photometry was underestimated by approximately 10%. We also found that the described photometric correction procedure can be the source of additional
noise (specifically for that field) if the correction factor is computed and applied to each individual image. Indeed, in that case, the correction is not simply a scaling factor, but seems to generate more high frequency fluctuations (typically of about an hour length). The reason is that for WASP-19, we applied the OIS on a small crop (600 × 600 pixels) rather than on the full image to increase the OIS precision (recalling that the kernel is allowed to vary according to second order variations). The WASP-19 field is not as crowded as other of our fields where the correction relies on much larger star counts. We therefore computed the photometric compensation factor for each image individually, and used a temporally smoothed version of it to compensate for the original OIS data. In that way, the original signal to noise is preserved, while correctly compensating for the photometric bias, mostly visible when deriving the primary transit parameters. Note that without compensating for the 10% photometric bias, the obtained primary transit parameters are way beyond the ones obtained with the compensated data (including error bars). The compensated data produce parameters that are totally consistent with values derived in previous papers (e.g. Anderson et al. 2010). Especially in Hellier et al. (2011) a WASP-19b transit lightcurve obtained with the NTT in the Gunn r-band is shown (see their Fig. 1 bottom), that was recorded just three months prior to our own observations, and is totally consistent with our own results.
Appendix A.5: Comparison between aperture photometry and OIS
Figure A.2 is a comparison between the residuals obtained for both the aperture photometry and the OIS algorithms in the whole WASP-19 field. The lightcurve calibration procedure is identical for both algorithms (only the raw lightcurves are different).
Appendix B: Day-to-day transit lightcurves
 |
Fig. B.1
Day-to-day lightcurves of the primary transits events, along with the best-fit model (from parameters of Table 2) overplotted in red, and the residual points, shifted in ordinate for clarity. |
| Open with DEXTER | |
Basic data and primary transit parameters for each of the observing night.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


