| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201218769 | |
| Published online | 11 September 2012 | |
Online material
Appendix A: Methods
A.1. Principal component analysis
Principal component analysis (PCA) is well-known to astronomers. It is not a partitioning method: its aim is instead to reduce the dimensionality of the parameter space. From the correlation matrix, PCA builds eigenvectors (the principal components) that are orthogonal and linear combinations of the physical parameters. These eigenvectors usually have no physical meaning. In general, most of the variance of the sample can be represented with only a few principal components (those having an eigenvalue greater than 1). They thus give a simpler representation of the data by eliminating the correlations between physical parameters. Strongly correlated parameters are gathered in the same eigenvector, and the most important parameters (with respect to variance) are the ones with the highest coefficient (loading) in each eigenvector. The physical interpretation must be made back in the real parameter space.
PCA is thus very efficient at reducing the parameter space to supposedly uncorrelated components and helps in detecting the most discriminant or discriminating parameters. The number of significant eigenvectors gives an idea of the number of parameters necessary to describe the sample. Principal components can also be used for subsequent cluster or cladistic analyses.
There is however a caveat to be kept in mind. PCA eliminates all correlations, regardless of whether they are causal. It is extremely useful to remove any redundancies, as well as physical correlations between two parameters indicating the same underlying process. However, PCA also removes evolutionary correlations (which are called “spurious” or confounding in statistics, Fraix-Burnet 2011), for instance between two parameters that are independent but vary with time. The log σ-Mg2 correlation for early-type galaxies (see Fraix-Burnet et al. 2010) is a good example. Such independent evolutions are lost through the PCA reduction of dimensionality.
A.2. Minimum contradiction analysis
Partitioning objects consists in producing some order. In some cases, i.e. in either hierarchical clustering or cladistics, the arrangement of the objects can be represented on a tree. A tree is a graph representing the objects as the leaves with a unique path between any two vertices. A bifurcating tree has internal vertices that all have a degree of at most 3 (at most 3 branches connect to any such vertex).
By indexing circularly all the leaves of a planar representation of a weighted binary tree, one obtains a perfect order, meaning that the corresponding ordered distance-matrix fulfills all Kalmanson inequalities. Generally speaking, the Kalmanson inequalities are fulfilled if the ordered distance matrix corresponds to a weighted binary tree or a superposition of binary trees (Thuillard & Moulton 2011). The difference between the perfect order and the order one obtains with a given dataset is called the contradiction. The minimum contradiction corresponds to the best order one can get.
The minimum contradiction analysis (Thuillard 2007, 2008, MCA) finds this best order. It is a powerful tool for ascertaining whether the parameters can lead to a tree-like arrangement of the objects (Thuillard & Fraix-Burnet 2009). Using the parameters that fulfil this property, the method then performs an optimisation of the order and provides groupings with an assessment of their robustness.
For taxa indexed according to a circular order, the distance matrix, which is defined to be
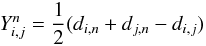 fulfils the
so-called Kalmanson inequalities (Kalmanson 1975):
fulfils the
so-called Kalmanson inequalities (Kalmanson 1975):
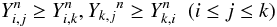 (A.1)where
di,j is the pairwise distance between
taxon i and j. The matrix element
(A.1)where
di,j is the pairwise distance between
taxon i and j. The matrix element
 is the
distance between a reference node n and the path
i-j. The diagonal elements
is the
distance between a reference node n and the path
i-j. The diagonal elements
 correspond to
the pairwise distance between the reference node n and the
taxon i.
correspond to
the pairwise distance between the reference node n and the
taxon i.
The contradiction on the order of the taxa can be defined as
 (A.2)for
any i,j,k ≠ n. The best order of a distance matrix
is, by definition, the order minimizing the contradiction (Thuillard 2007, 2008). Thuillard & Fraix-Burnet (2009) showed that
the perfect order is linked to the convexity of the variables in the parameter space,
and is obtained for specific properties of the variables along the order. It is then
possible to detect the discriminant potentiality of the variables. This is exactly
what is done in Sect. 3.2.
(A.2)for
any i,j,k ≠ n. The best order of a distance matrix
is, by definition, the order minimizing the contradiction (Thuillard 2007, 2008). Thuillard & Fraix-Burnet (2009) showed that
the perfect order is linked to the convexity of the variables in the parameter space,
and is obtained for specific properties of the variables along the order. It is then
possible to detect the discriminant potentiality of the variables. This is exactly
what is done in Sect. 3.2.
A.3. Cladistic analysis
Cladistics seeks to establish evolutionary relationships between objects. It is a non-parametric character-based phylogenetic method, also called a maximum parsimony method. It does not use distances, because there is no assumption about the metrics of the parameter space. The “characters” are instead traits, descriptors, observables, or properties, which can be assigned at least two states characterizing the evolutionary stage of the objects for that character. The use of this approach in astrophysics is known as astrocladistics (for details and applications, see Fraix-Burnet et al. 2006b,c, 2009, 2010). Simply speaking, the characters here are the parameters, the (continuous) values of which supposedly evolve with the level of diversification of the objects. The maximum parsimony algorithm looks for the simplest arrangement of objects on a bifurcating tree. The complexity of the arrangement is measured by the total number of “steps” (i.e. changes in all parameter values) along the tree.
The success of a cladistic analysis much depends on the behaviour of the parameters. In particular, it is sensitive to redundancies, incompatibilities, too much variability (reversals), and parallel and convergent evolutions. It is thus a very good tool for investigating whether a given set of parameters can lead to a robust and pertinent diversification scenario.
In the present study, we used the same kind of analysis as in our previous papers on astrocladistics. We discretized the parameters into 30 equal-width bins, which play the role of discrete evolutionary states. This choice of 30 bins is justified by a fair representation of diversity, a stability of the analysis in the sense that the result does not depend on the number of bins, and a bin width roughly corresponding to the typical order of magnitude of the uncertainties (i.e. 7%, see Fraix-Burnet et al. 2009). We also adopted the parsimony criterion, which consists in finding the simplest evolutionary scenario that can be represented on a tree. Our maximum parsimony searches were performed using the heuristic algorithm implemented in the PAUP*4.0b10 (Swofford 2003) package, with the Multi-Batch Paup Ratchet method3. The results were interpreted with the help of the Mesquite software (Maddison & Maddison 2004) and the R-package (used for graphics and statistical analyses).
Fitness of parameters on the cladograms obtained for each subset as represented by the Rescaled Consistency Index (RCI).
Making cladistic analyses with different sets of parameters both helps to find the most robust result and gives interesting information on the behaviour of the parameters themselves. The robustness of cladograms is always difficult to assess objectively, so we use a criterion similar to that of other statistical distance analyses: if a similar result is found by using different conditions or methods, then it can be considered as reasonably robust. We applied four possible tests here:
-
1.
The occurrence of a branching pattern among most parsimonious trees: with so few parameters, many equally parsimonious trees are found, often arbitrarily limited to 1000. The majority-rule consensus of all of them yields a percentage of occurrence for each node. The higher this percentage, the higher the probability that this node is “robust”.
-
2.
The agreement of branching patterns between sub-sample analyses, which can be called “internal consistency”: by making analyses of several sets of arbitrarily selected sub-samples, we can check whether a given pattern is present on trees found with larger samples, including the full tree.
-
3.
The comparison between different sets of parameters: any result should preferably not depend too much on a single parameter. Adding or removing a parameter should not drastically change the tree.
-
4.
A comparison with the results of a cluster analysis: distance-based methods are totally independent, so any agreement can instill us a fair confidence in the result.
The full sample of 424 galaxies was divided into three subsamples with 105 objects each and a fourth one with 109 objects. The first and fourth subsamples were found to belong exclusively to clusters 1 and 3, respectively, of the cluster analysis. The diversity in the first subsample is less than for the others, so that the resulting tree is generally less well-resolved. The two first subsamples were also gathered to form a 210-object subsample, as well as the two last ones that form a 214-object subsample. Analyses were performed with these six subsamples, as well as the full sample. We then estimated the internal consistency by comparing the seven trees two by two and by eye (with the help of the program cophyloplot in the R-package, which connects a given object between the two trees).
This procedure was applied to each of the eight-parameter subsets given in Table 1. Subsets 5c, 5cA, 6cA, and 3c show a rather good internal consistency, 4c, 7c, and 6c that which is fairly good, and finally 8c and 10c that which is not so good.
This already shows that the optimal number of parameters is around 5, 6, or at most 7. This is in excellent agreement with the PCA analysis (Sect. A.1).
If we compare the trees obtained with the full sample for the eight-parameter subsets, we find that subset 5c is very consistent with 6c, 7c, and 8c. In addition, 5c, 6c, 5cA, and 6cA are in good mutual agreement, while this is not the case for 6c, 7c, and 8c.
In Table A.2, we show for each tree the Rescaled Consistency Index (RCI), which measures the fitness of a parameter on the phylogeny depicted by the tree. The higher the RCI (indeed the closer it is to 1), the more discriminant the parameter. In other words, parameters with higher RCI are the most responsible for the structure of the tree. The absolute value depends on the number of objects and parameters, so it cannot be used to compare trees obtained with different data. Here, we can only use it to compare parameters for a given tree. In Table A.2, the parameters are ordered according to RCI.
 |
Fig. A.1
Plots showing the jumps as defined in Sect. A.4. Top: jumps for the PCA+CA analysis (Sect. 4.1). Bottom: jumps for the cluster analysis with the six parameters (Sect. 4.2). |
| Open with DEXTER | |
When Mg b and [MgbFe]′ are present together in a subset, they dominate the shape of the tree (sets 5cA, 6cA, 8c, and 10c), log σ and D/B being right after them. Mg b and [MgbFe]′ are obviously redundant because they are very well-correlated and are more or less the same measure. Hence, they cannot be used simultaneously in the cladistic analysis, and the trees that we find are more linear than the others. In contrast, log σ and D/B are not at all correlated, but are always together, and dominate the tree shape when Mg b is not present together with [MgbFe]′. In addition, NaD is very discriminant, and only roughly correlated with log σ and [MgbFe]′.
If we compare the clusters obtained with the clustering analysis, the agreement decreases roughly for 6c, 7c, 5A, 3c, 5c, 4cA, 8c, and 10c, the winner being undoubtedly 6c. The corresponding tree with the groups is shown in Fig. 3.
A.4. Cluster analysis
In the present study, we adopted K-means partitioning algorithm of clustering following MacQueen (1967). This method constructs K clusters using a distance measure (here Euclidean). The data are classified into K groups around K centres, such that the distance of a member object of any particular cluster (group) from its centre is minimal compared to its distance from the centres of the remaining groups. The requirement for the algorithm is that each group must contain at least one object and each object must belong to exactly one group, so there are at most as many groups as there are objects. Partitioning methods are applied (Whitmore 1984; Murtagh 1987; Chattopadhyay & Chattopadhyay 2006, 2007; Babu et al. 2009; Chattopadhyay et al. 2009a; Chattopadhyay et al. 2010), if one wishes to classify the objects into K clusters where K is fixed. Cluster centres were chosen based on a group average method, which ensures that the process is almost robust (Milligan 1980).
To achieve an optimum choice of K, the algorithm is run for
K = 2,3,4, etc. For each value of
K, the value of a distance measure
dK (called the distortion) is
computed as
dK = (1/p)minxE [(xK − cK)′(xK − cK)] ,
which is defined as the distance of the
xK vector (values of the parameters)
from the centre cK where p is the order
of the xK vector. If
 is the
estimate of dK at the
Kth point, then the optimum number of clusters is determined by the
sharp jump in the curve
is the
estimate of dK at the
Kth point, then the optimum number of clusters is determined by the
sharp jump in the curve  vs. K
(Sugar & James 2003). The jumps as a
function of K for our PCA+CA and CA analyses are shown in Fig. A.1.
vs. K
(Sugar & James 2003). The jumps as a
function of K for our PCA+CA and CA analyses are shown in Fig. A.1.
Appendix B: Analysis with log σ, log re, Brie and Mg2, and error bars
B.1. Analysis with logσ, log re, Brie and Mg2
We complemented the study presented in this paper with the analysis of our sample with the four parameters (log re, log σ, Brie, and Mg2) as in Fraix-Burnet et al. (2010). We used the same three multivariate techniques (cluster analysis, Miminimum Contradiction Analysis, and cladistics) as presented in Sect. 2.2 and Appendix A.
 |
Fig. B.1
Projection of the trees onto the fundamental plane for three cases: the analysis of this Appendix B and the one by Fraix-Burnet et al. (2010) both using the four parameters of the fundamental plane, and the principal study of the present paper with six parameters. Thick lines represent the “trunk” of the trees, while the small branches relate the trunks to the mean of each group. For clarity, results are compared two by two, and only the trunks are shown for the three studies on the lower right diagram. These are evolutionary tracks in the sense of diversification, and not the path of evolution for a single galaxy. |
| Open with DEXTER | |
The resulting tree is less structured (more galaxies lie on individual branches) than the one obtained in the present paper using six parameters. This can be explained by log re and Mg2 not having been found to be discriminant parameters for the considered sample. It is also less structured than in Fraix-Burnet et al. (2010) which uses the same four parameters, which is probably due to the problems in determining of log re.
To summarize the results, we show the projection of the three trees – the one obtained in this paper with six parameters, the one obtained here with four parameters, and the one of Fraix-Burnet et al. (2010) – onto the fundamental plane (log σ vs. Brie) without the data points (Fig. B.1). Globally, there is good agreement and the groupings are consistent. However, the projected tree from the present Appendix departs from the other two in the top half of the figure. This is because this tree is less structured than the others, so that instead of having one or two groups at this level, there is a sequence of single branches that makes the trunk of the tree to “follow” more closely individual objects.
 |
Fig. B.2
Correspondence between the effective radius computed in two separate ways. |
| Open with DEXTER | |
B.2. Influence of re and error bars on the partitioning
The effective radius log re in our sample is recomputed through a statistical relation between the linear diameter of the galaxy (Dn) and its velocity dispersion (σ), which was determined in another paper (Bernardi et al. 2002). The reason given by Ogando et al. (2008) is that, due to the very low redshift of the galaxies in the sample, “the conversion of re in arcseconds to kpc needs a reliable determination of the galaxy distance (D). Considering just the redshift to calculate D, we may incur in error due to the peculiar motion of galaxies. Thus, we adopted D given by the Dn vs. σ relation (Bernardi et al. 2002) to calculate re in kpc.” However, this relation was obtained with some assumptions (such as the identical properties of galaxies in several clusters) and introduces a dependence of log re (through D) on log σ.
The two radii (Fig. B.2) are quite well-correlated with each other, but the dispersion is relatively large. We performed two cladistic analyses with the four parameters of the fundamental plane (log re, log σ, Brie, and Mg2) as above using the two determinations of the effective radius. The agreement between the two results is only fair. This can be explained by the relatively important discrepancy between the two different values of re (median difference of 10%). This however is similar to the uncertainty in log re, but much larger thn for the other parameters. In addition, the radius or dimension of galaxies does not appear as a discriminant parameter in the study presented in this paper. Hence, it is not so surprising that analyses using this parameter are not very stable.
We now consider the robustness of our clustering result for the six-parameter analysis when taking error measurements into account. It is statistically a very challenging task to assess the influence of the errors. However, cladistics can easily take into account the error bars since the optimisation criterion in all analyses performed so far in astrocladistics use the parsimony criterion: among all the possible arrangements of the objects on trees, the simplest evolutionary scenario is retained. The parcimony is measured by using the number of “steps”, that is the total number of changes in parameter values along all the branches of the tree. If a missing value or an uncertain one (given by a range of values) is included in the data matrix, all possible values are considered and the ones corresponding to the simplest tree is favored. This simply increases the number of possible cases to consider. We note that all possible values within the range alllowed by measurement uncertainties are given the same weight, whereas the probability distribution is generally expected to be higher at the central value (ideally Gaussian).
We performed a cladistic analysis similar to that in Fig. 3 using the error bars given in Ogando et al. (2008) and Alonso et al. (2003) for log σ and Brie, and for D/B we considered the error given for log re in Alonso et al. (2003), There errors are shown in Fig. B.3. For NaD, [MgbFe]′, and OIII, we assumed a face value of 10%, which is the upper limit estimated by Ogando et al. (2008) for all the Lick index values.
 |
Fig. B.3
Errors in log σ, Brie, and log re (taken for the errors in D/B). |
| Open with DEXTER | |
 |
Fig. B.4
The most parsimonious tree found with cladistics taking uncertainties in the parameters into account. The colours correspond to the groups defined in Fig. 3. |
| Open with DEXTER | |
The resulting tree shown in Fig. B.4 is slightly less structured than the one in Fig. 3 but most groups are grossly preserved. Clad3 appears to be mixed with Clad1 and Clad5 to be mixed with Clad6. In addition, Clad7 and Clad8 are somewhat mixed with each other. Interestingly, these behaviours are similar to those inferred from the comparison with the partitioning derived from the cluster analysis. In addition, the agreement is quite satisfactory given the large uncertainties for half of the
parameters (the Lick indices), a face value given to these uncertainties, and the equal probability given to all values within the range of uncertainty.
These results shows that the cladistic analysis is relatively robust to measurement errors, as found through the comparison with different clustering methods.
Appendix C: Supplementary figures
 |
Fig. C.1
Same boxplots as in Fig. 4 but for the cluster partitioning. Colours are the one given in Fig. 2. |
| Open with DEXTER | |
 |
Fig. C.2
Scatter plots showing evolutionary correlations, like Fig. 5, but for the cluster partitioning. Colours are the same as in Fig. C.1. |
| Open with DEXTER | |
 |
Fig. C.3
Comparison of the positions of the groups found in Fraix-Burnet et al. (2010) and those of the present paper, as projected onto the fundamental plane. The colour-coded ellipses are the inertia ellipses for each group from the present paper, and the black ellipse is the one for the group from Fraix-Burnet et al. (2010) indicated on top each graph. See also Fig. 8. |
| Open with DEXTER | |
 |
Fig. C.4
Comparison of the positions of the groups found in Fraix-Burnet et al. (2010) and those of the present paper, as projected onto the log re vs. Mdyn diagram. The colour-coded ellipses are the inertia ellipses for each group from the present paper, and the black ellipse is the one for the group from Fraix-Burnet et al. (2010) indicated on top each graph. See also Fig. 9. |
| Open with DEXTER | |
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


