| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 19 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219119 | |
| Published online | 01 June 2012 | |
Online material
Data on clusters.
Data on superclusters.
Appendix A: Multimodality of clusters
We employ two 3D methods to search for substructure in clusters. With Mclust package (Fraley & Raftery 2006) from R, an open-source free statistical environment developed under the GNU GPL (Ihaka & Gentleman 1996, http://www.r-project.org) we search for an optimal model for the clustering of the data among models with varying shape, orientation and volume, under assumption that the multivariate sample is a random sample from a mixture of multivariate normal distributions. Mclust finds the optimal number of components and calculates for every galaxy the probabilities to belong to any of the components which are used to calculate the uncertainties for galaxies to belong to a component. The mean uncertainty for the full sample is used as a statistical estimate of the reliability of the results. The calculations in E12 showed that uncertainties are small, their values can be found in online tables of E12. We tested how the possible errors in the line-of-sight positions of galaxies affect the results of Mclust, shifting randomly the peculiar velocities of galaxies 1000 times and searching each time for the components with Mclust. The random shifts were chosen from a Gaussian distribution with the dispersion equal to the sample velocity dispersion of galaxies in a cluster. The number of the components found by Mclust remained unchanged, demonstrating that the results of Mclust are not sensitive to such errors.
The Dressler-Shectman (DS) test searches for deviations of the local velocity mean and dispersion from the cluster mean values. The algorithm starts by calculating the mean velocity (vlocal) and the velocity dispersion (σlocal) for each galaxy of the cluster, using its n nearest neighbours. These values of local kinematics are compared with the mean velocity (vc) and the velocity dispersion (σc) determined for the entire cluster of Ngal galaxies. The differences between the local and global kinematics are quantified by
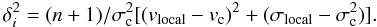 The cumulative deviation Δ = Σδi is used as a statistic for quantifying (the significance of) the substructure. The results of the DS-test depend on the number of local galaxies n. We use
The cumulative deviation Δ = Σδi is used as a statistic for quantifying (the significance of) the substructure. The results of the DS-test depend on the number of local galaxies n. We use 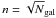 , as suggested by Pinkney et al. (1996). The Δ statistic for each cluster should be calibrated by Monte Carlo simulations. In Monte Carlo models the velocities of galaxies are randomly shuffled among the positions. We ran 25 000 models for each cluster and calculated every time Δsim. The significance of having substructure (the pΔ-value) can be quantified by the ratio N(Δsim > Δobs)/Nsim – the ratio of the number of simulations in which the value of Δ is larger than the observed value, and the total number of simulations. The smaller the pΔ-value, the larger is the probability of substructure.
, as suggested by Pinkney et al. (1996). The Δ statistic for each cluster should be calibrated by Monte Carlo simulations. In Monte Carlo models the velocities of galaxies are randomly shuffled among the positions. We ran 25 000 models for each cluster and calculated every time Δsim. The significance of having substructure (the pΔ-value) can be quantified by the ratio N(Δsim > Δobs)/Nsim – the ratio of the number of simulations in which the value of Δ is larger than the observed value, and the total number of simulations. The smaller the pΔ-value, the larger is the probability of substructure.
Appendix B: Luminosity density field and superclusters
To calculate the luminosity density field, we calculate the luminosities of groups first. In flux-limited samples, galaxies outside the observational window remain unobserved. To take into account the luminosities of the galaxies that lie outside the sample limits also we multiply the observed galaxy luminosities by the weight Wd. The distance-dependent weight factor Wd was calculated as 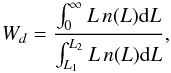 (B.1)where L1,2 = L⊙100.4(M⊙ − M1,2) are the luminosity limits of the observational window at a distance d, corresponding to the absolute magnitude limits of the window M1 and M2; we took M⊙ = 4.64 mag in the r-band (Blanton & Roweis 2007). Due to their peculiar velocities, the distances of galaxies are somewhat uncertain; if the galaxy belongs to a group, we use the group distance to determine the weight factor. Details of the calculations of weights are given also in Tempel et al. (2011) and in Einasto et al. (2011c).
(B.1)where L1,2 = L⊙100.4(M⊙ − M1,2) are the luminosity limits of the observational window at a distance d, corresponding to the absolute magnitude limits of the window M1 and M2; we took M⊙ = 4.64 mag in the r-band (Blanton & Roweis 2007). Due to their peculiar velocities, the distances of galaxies are somewhat uncertain; if the galaxy belongs to a group, we use the group distance to determine the weight factor. Details of the calculations of weights are given also in Tempel et al. (2011) and in Einasto et al. (2011c).
To calculate a luminosity density field, we convert the spatial positions of galaxies ri and their luminosities Li into spatial (luminosity) densities using kernel densities (Silverman 1986): 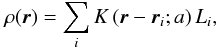 (B.2)where the sum is over all galaxies, and K(r;a) is a kernel function of a width a. Good kernels for calculating densities on a spatial grid are generated by box splines BJ. Box splines are local and they are interpolating on a grid:
(B.2)where the sum is over all galaxies, and K(r;a) is a kernel function of a width a. Good kernels for calculating densities on a spatial grid are generated by box splines BJ. Box splines are local and they are interpolating on a grid: 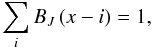 (B.3)for any x and a small number of indices that give non-zero values for BJ(x). We use the popular B3 spline function:
(B.3)for any x and a small number of indices that give non-zero values for BJ(x). We use the popular B3 spline function: 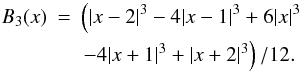 (B.4)The (one-dimensional) B3 box spline kernel
(B.4)The (one-dimensional) B3 box spline kernel 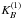 of the width a is defined as
of the width a is defined as 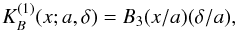 (B.5)where δ is the grid step. This kernel differs from zero only in the interval x ∈ [ − 2a,2a] . It is close to a Gaussian with σ = 0.6 in the region x ∈ [ − a,a] , so its effective width is 2a (see, e.g., Saar 2009). The kernel preserves the interpolation property exactly for all values of a and δ, where the ratio a/δ is an integer. (This kernel can be used also if this ratio is not an integer, and a ≫ δ; the kernel sums to 1 in this case, too, with a very small error.) This means that if we apply this kernel to N points on a one-dimensional grid, the sum of the densities over the grid is exactly N.
(B.5)where δ is the grid step. This kernel differs from zero only in the interval x ∈ [ − 2a,2a] . It is close to a Gaussian with σ = 0.6 in the region x ∈ [ − a,a] , so its effective width is 2a (see, e.g., Saar 2009). The kernel preserves the interpolation property exactly for all values of a and δ, where the ratio a/δ is an integer. (This kernel can be used also if this ratio is not an integer, and a ≫ δ; the kernel sums to 1 in this case, too, with a very small error.) This means that if we apply this kernel to N points on a one-dimensional grid, the sum of the densities over the grid is exactly N.
The three-dimensional kernel 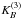 is given by the direct product of three one-dimensional kernels:
is given by the direct product of three one-dimensional kernels: 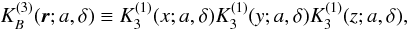 (B.6)where r ≡ { x,y,z } . Although this is a direct product, it is isotropic to a good degree (Saar 2009).
(B.6)where r ≡ { x,y,z } . Although this is a direct product, it is isotropic to a good degree (Saar 2009).
The densities were calculated on a cartesian grid based on the SDSS η, λ coordinate system. The grid coordinates are calculated according to Eq. (3). We used an 1 h-1 Mpc step grid and chose the kernel width a = 8 h-1 Mpc. This kernel differs from zero within the radius 16 h-1 Mpc, but significantly so only inside the 8 h-1 Mpc radius. As a lower limit for the volume of superclusters we used the value (a/2) h-1 Mpc3 (64 grid cells). We also used density field with the kernel widths a = 4 h-1 Mpc, a = 8 h-1 Mpc, and a = 16 h-1 Mpc to characterise the environmental density around clusters. Before extracting superclusters we apply the DR7 mask constructed by Arnalte-Mur (Martínez et al. 2009; Liivamägi et al. 2012) to the density field and convert densities into units of mean density. The mean density is defined as the average over all pixel values inside the mask. The mask is designed to follow the edges of the survey and the galaxy distribution inside the mask is assumed to be homogeneous.
Appendix C: Minkowski functionals and shapefinders
For a given surface the four Minkowski functionals (from the first to the fourth) are proportional to the enclosed volume V, the area of the surface S, the integrated mean curvature C, and the integrated Gaussian curvature χ. Consider an excursion set Fφ0 of a field φ(x) (the set of all points where the density is higher than a given limit, φ(x ≥ φ0)). Then, the first Minkowski functional (the volume functional) is the volume of this region (the excursion set): 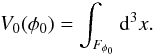 (C.1)The second Minkowski functional is proportional to the surface area of the boundary δFφ of the excursion set:
(C.1)The second Minkowski functional is proportional to the surface area of the boundary δFφ of the excursion set: 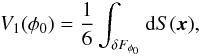 (C.2)(but it is not the area itself, notice the constant). The third Minkowski functional is proportional to the integrated mean curvature C of the boundary:
(C.2)(but it is not the area itself, notice the constant). The third Minkowski functional is proportional to the integrated mean curvature C of the boundary: 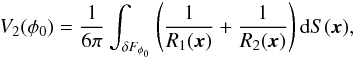 (C.3)where R1(x) and R2(x) are the principal radii of curvature of the boundary. The fourth Minkowski functional is proportional to the integrated Gaussian curvature (the Euler characteristic) of the boundary:
(C.3)where R1(x) and R2(x) are the principal radii of curvature of the boundary. The fourth Minkowski functional is proportional to the integrated Gaussian curvature (the Euler characteristic) of the boundary: 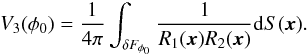 (C.4)
(C.4)
At high (low) densities this functional gives us the number of isolated clumps (void bubbles) in the sample (Martínez & Saar 2002; Saar et al. 2007): 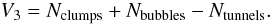 (C.5)As the argument labelling the isodensity surfaces, we chose the (excluded) mass fraction mf – the ratio of the mass in the regions with the density lower than the density at the surface, to the total mass of the supercluster. When this ratio runs from 0 to 1, the iso-surfaces move from the outer limiting boundary into the centre of the supercluster, i.e., the fraction mf = 0 corresponds to the whole supercluster, and mf = 1 – to its highest density peak.
(C.5)As the argument labelling the isodensity surfaces, we chose the (excluded) mass fraction mf – the ratio of the mass in the regions with the density lower than the density at the surface, to the total mass of the supercluster. When this ratio runs from 0 to 1, the iso-surfaces move from the outer limiting boundary into the centre of the supercluster, i.e., the fraction mf = 0 corresponds to the whole supercluster, and mf = 1 – to its highest density peak.
The first three functionals were used to calculate the shapefinders (Sahni et al. 1998; Shandarin et al. 2004; Saar 2009). The shapefinders are defined as a set of combinations of Minkowski functionals: H1 = 3V/S (thickness), H2 = S/C (width), and H3 = C/4π (length). The shapefinders have dimensions of length and are normalized to give Hi = R for a sphere of radius R. For smooth (ellipsoidal) surfaces, the shapefinders Hi follow the inequalities H1 ≤ H2 ≤ H3. Oblate ellipsoids (pancakes) are characterised by H1 ≪ H2 ≈ H3, while prolate ellipsoids (filaments) are described by H1 ≈ H2 ≪ H3. Sahni et al. (1998) also defined two dimensionless shapefinders K1 (planarity) and K2 (filamentarity): K1 = (H2 − H1)/(H2 + H1) and K2 = (H3 − H2)/(H3 + H2). In the (K1,K2)-plane filaments are located near the K2-axis, pancakes near the K1-axis, and ribbons along the diameter, connecting the spheres at the origin with the ideal ribbon at (1,1). In Einasto et al. (2007c) we calculated typical morphological signatures of a series of empirical models that serve as morphological templates to compare with the characteristic curves for superclusters in the (K1,K2)-plane.
Appendix D: Data on selected clusters
Data on most luminous clusters.
Data on unimodal clusters.
Data on multimodal clusters.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


