| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 25 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201116844 | |
| Published online | 22 July 2011 | |
Online material
Appendix A: A cheap P(D) estimator
In addition to directly detected sources and to stacking of 24 μm dense catalogs, further information about the shape of PACS number counts comes from the statistical properties of observations, probing the counts at even fainter fluxes. The “probability of deflection”, or P(D) distribution, is basically the distribution of pixel values in a map (see Sect. 4).
For a large density of sources, the contribution to the P(D) is a Poisson distribution with a large mean value, convolved with the instrumental noise (typically assumed to be Gaussian). Generally speaking, for sufficiently steep number counts at faint flux densities, the depth reached with the P(D) analysis is significantly higher than what is provided by individually-detected sources, and is a powerful tool to probe counts slopes in cases dominated by confusion.
Given differential number counts dN/dS, and a beam function (e.g., PSF) f(θ,φ), describing the point-source spatial-response at position x, the probability of deflection P(D) can be written as (e.g., Patanchon et al. 2009): 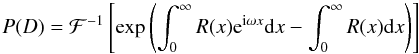 (A.1)or, alternatively, isolating the real part only (e.g., Franceschini et al. 2010):
(A.1)or, alternatively, isolating the real part only (e.g., Franceschini et al. 2010): 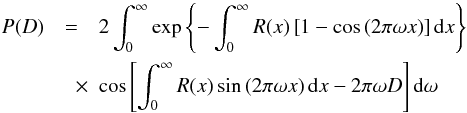 (A.2)where the mean number of source responses of intensity x in the beam is given by:
(A.2)where the mean number of source responses of intensity x in the beam is given by: 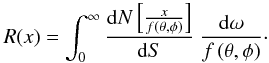 (A.3)We defer to Patanchon et al. (2009), Franceschini et al. (2010), Glenn et al. (2010) for a full treatment and description of the P(D) formalism. Only in the case of very simple dN/dS functional forms and trivial beams (e.g., Gaussian), the above equations can be solved analytically. For an effective beam that is not strictly positive, or is not azimuthally symmetric, it is necessary to use the full 2D beam map.
(A.3)We defer to Patanchon et al. (2009), Franceschini et al. (2010), Glenn et al. (2010) for a full treatment and description of the P(D) formalism. Only in the case of very simple dN/dS functional forms and trivial beams (e.g., Gaussian), the above equations can be solved analytically. For an effective beam that is not strictly positive, or is not azimuthally symmetric, it is necessary to use the full 2D beam map.
For example, the Herschel/PACS beam is characterized by 3 prominent lobes, which cannot be described analytically. In such a case, if one likes to account for the real beam function, a numerical treatment of R(x), and possibly P(D) is necessary.
Finally, in case of real observations, the instrumental noise contribution to pixel flux densities must be included.
A.1. The numerical P(D) approach
Given an instrumental PSF f(θ,φ) and a number counts model dN/dS, it is possible to predict the pixel flux density distribution of a map with M pixels, simply rolling random numbers. We describe here the principles of the method we developed in the frame of the PEP survey. This approach turns out to be of simple implementation, avoiding integrations of oscillating functions or Fourier Transforms, and it is accessible to any user with a basic knowledge of random number generators. Furthermore, it avoids any analytic simplification of the beam function, thus allowing to employ the real instrumental PSF, regardless of how complex its bi-dimensional profile is.
For a given dN/dS, we describe how a synthetic P(D) is computed. The adopted form of number counts and fitting technique are described in the next Section. Parameters are varied by means of a MCMC engine and for each realization a new P(D) is computed and compared to the observed data.
The input information needed by the P(D) numerical algorithm are:
-
description of number counts, dN/dS;
-
beam function, e.g., in form of an observed PSF 2D map;
-
value of instrumental noise.
Further secondary inputs, derived from the three primaries above, are:
-
the maximum radius rmax in pixels from a given source within which apixel is affected by the source itself, e.g., the radius at which 99%of the observed PSF flux is enclosed; if the pixel scale of the map is αarcsec/pix, the corresponding angular radius is αrmax;
-
the total expected number, N0, of sources within the solid angle Ω defined by rmax, simply given by the integral of number counts:
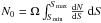
-
the cumulative probability that a random source has a flux lower than S, given by:
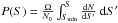 .
.
As mentioned above, the procedure relies on several dice rolls, using random numbers to determine the actual number of sources expected to contribute to each pixel of the map, the distance of the given source to the pixel, the fluxes of sources.
-
Step 1.
We assume that the distribution of sources in the skyis randomly uniform, i.e. we ignore the clustering prop-erties of sources in the sky. Clustering would mainly af-fect the P(D) over scales larger than the size of the GOODS-S field under exam here (e.g., Glennet al. 2010; Vieroet al. 2009; Lagacheet al. 2007). Given N0, the number of sources affecting the given pixel in the current realization is a random Poisson deviate for expected N0. This number is recomputed for each pixel and each dN/dS realization.
-
Step 2.
For each source affecting the given pixel, it is necessary to determine the fraction fi of flux affecting the pixel. Roll N random, uniformly distributed positions, inside rmax (defined either by r,φ or by x,y coordinates). Based on the position of the given source, and the beam function, derive the fraction of flux affecting the pixel for each source.
-
Step 3.
Finally assign a random flux Si to each of the N sources affecting the given pixel, according to the input dN/dS. To this aim, the probability P(S) (defined above) is used to transform a flat random number distribution in the needed flux values.
Assuming that any further background has been subtracted from the map, the flux of the given pixel is finally given by 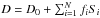 , where D0 is the term describing pure noise (i.e. random flux, in case of no sources at all) and is given by a Gaussian deviate as wide as the noise measured on actual PEP rms maps (see Table 1).
, where D0 is the term describing pure noise (i.e. random flux, in case of no sources at all) and is given by a Gaussian deviate as wide as the noise measured on actual PEP rms maps (see Table 1).
A.2. Number counts model and minimization
Number counts are modeled similarly to Patanchon et al. (2009) and Glenn et al. (2010). We adopt a simple, parametric model, defined by the differential counts dN/dS at a set of flux density knots, or nodes. The model is defined within a Smin and Smax lower and upper flux boundaries; outside of this flux range, we simply set dN/dS to zero. Between nodes, number counts are described as power-laws, connecting at knots.
We used a Markov-Chain Monte Carlo (MCMC) sampling of the parameter space, to explore the likelihood function of the model to reproduce the observed P(D). We use a Metropolis-Hastings algorithm as our MCMC sampler. In order for this sampler to converge efficiently, we draw new steps from univariate Gaussian distributions, whose widths were given by dummy MCMC runs.
The position of knots and the corresponding amplitude of counts are free parameters, and are varied at each MCMC map realization. The upper boundary of the covered flux range is fixed to 100 mJy, a value driven by the limits of observed, resolved counts in GOODS-S. In order to minimize the number of free parameters, and further degeneracies, we limit the description of number counts to a broken power-law with three sections, for a total of seven free parameters (3 positions and 4 amplitudes).
In the past, a standard approach was to subtract bright individually detected sources from the P(D) analysis, and work only at the faint side, but it has been shown that a more robust estimate of the source counts is obtained if the P(D) is fitted across the whole available flux density range (e.g., Patanchon et al. 2009). Therefore, to derive the observed P(D) to be reproduced, we use the observed science maps without subtracting any object.
Section 4, Figs. 8, 7 and Table 10 describe the results of the whole P(D) analysis.
A.3. Effects of map-making high-pass filtering
It is necessary to recall that PEP maps have been obtained by applying a high-pass filtering process along the data time-line, in order to get rid of 1/f noise. This procedure consist in a running-box median filter, and induces two different side effects onto PACS maps: 1) the background is naturally removed from the maps; 2) the PSF profile is eroded and wings are suppressed.
At very faint fluxes, and high source densities, close to and beyond the confusion limit, the contribution of sources to the model P(D) basically generates a “background” sheet of sources, which shifts the P(D) histogram to a non-zero peak and median. In principle, the source component of the P(D) is always positive, and the addition of noise generates the negative nearly-Gaussian behaviors at the faint side of P(D). The adopted high-pass filtering shifts the whole flux pixel distribution function to a zero peak/median. In order to take this into account, with the current form of PEP maps, we shift the model P(D) to the same zero peak, prior of fitting.
The second consequence of applying an high-pass filter is a modification of object profiles. Detected objects are masked and excluded from the median filter derivation. Tests were done adding simulated sources to the time-lines before masking and before high-pass filtering (see Popesso et al., in prep.; Lutz et al. 2011). The result is that the filtering modifies the fluxes of masked sources below the detection limit – by a factor ≤ 16%. In order to understand the impact of this on the P(D) analysis, we built simulated maps 20 times deeper than the GOODS-S 3σ threshold, once using an un-filtered (i.e. masked) PSF at all fluxes, and once using an un-filtered PSF above 3σ, but a filtered (unmasked) PSF below. The P(D) obtained in the two cases are well consistent to each other, with unit median ratio and a < 5% scatter across all fluxes; no systematic shift, nor skewness are observed.
PEP 100 μm number counts, normalized to the Euclidean slope.
PEP 160 μm number counts, normalized to the Euclidean slope.
PEP 100 μm number counts, normalized to the Euclidean slope, and split in redshift slices.
PEP 160 μm number counts, normalized to the Euclidean slope, and split in redshift slices.
© ESO, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


