Molecular absorption lines toward star-forming regions: a comparative study of HCO+, HNC, HCN, and CN

Home

All issues

Volume 520 (September-October 2010)

A&A, 520 (2010) A20

Online Material

Free Access

Issue		A&A Volume 520, September-October 2010


Article Number		A20
Number of page(s)		20
Section		Interstellar and circumstellar matter
DOI		https://doi.org/10.1051/0004-6361/201014283
Published online		23 September 2010

Online Material

Appendix A: Gaussian decomposition and calculation of column densities

Table A.1: HCO⁺ (0-1) absorption line analysis results.

Table A.2: HNC (0-1) absorption line analysis products.

Table A.3: HCN (0-1) absorption line analysis products.

Table A.4: CN (0-1) absorption line analysis products.

Tables A.1-A.4 contains the results of the Gaussian decompostion procedure that we have applied to the spectra. The column densities, given in the last columns, are derived assuming a single excitation temperature $T_{\rm ex}$ for all the levels of a given molecule as

$\begin{displaymath} N = Q(T_{\rm ex}) \frac{8 \pi \nu_0^{3}}{c^{3}} \frac{g_{\rm... ...h\nu_0/k T_{\rm ex}} \right]^{-1} \int \tau ~ {\rm d}\upsilon \end{displaymath}$

(A.1)

where $\nu_0$ , $g_{\rm u}$ , $g_{\rm l}$ and $A_{\rm ul}$ are the rest frequency, the upper and lower level degeneracies and the Einstein's coefficients of the observed transition, $Q(T_{\rm ex})$ is the partition funtion, and c is the speed of light. We also remind that for a Gaussian profile of peak opacity $\tau_0$ and FWHM $\Delta \upsilon$ , the opacity integral is $\int \tau ~ {\rm d}\upsilon = 1/2 ~ \sqrt{\pi/\ln{2}} ~ \tau_0 ~ \Delta \upsilon$ . For an excitation temperature of 2.73 K, Eq. (A.1) becomes

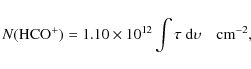
$\begin{displaymath}N({\rm HCO}^{+}) = 1.10 \times 10^{12} \int \tau ~ {\rm d}\upsilon \quad {\rm cm}^{-2}, \end{displaymath}$

(A.2)

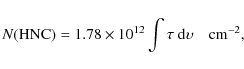
$\begin{displaymath}N({\rm HNC}) = 1.78 \times 10^{12} \int \tau ~ {\rm d}\upsilon \quad {\rm cm}^{-2}, \end{displaymath}$

(A.3)

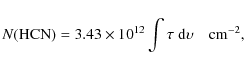
$\begin{displaymath}N({\rm HCN}) = 3.43 \times 10^{12} \int \tau ~ {\rm d}\upsilon \quad {\rm cm}^{-2}, \end{displaymath}$

(A.4)

and

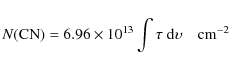
$\begin{displaymath}N({\rm CN}) = 6.96 \times 10^{13} \int \tau ~ {\rm d}\upsilon \quad {\rm cm}^{-2} \end{displaymath}$

(A.5)

using the HCO⁺ J=0-1, HNC J=0-1, HCN J,F=0,1-1,2, and CN J,F1,F=0,1/2,3/2-1,1/2,3/2 transitions respectively.

Appendix B: Impact of the abscissa uncertainty on the multi-Gaussian decomposition procedure

In a spectrum, the possible velocity substructures are systematically erased due to the finite velocity resolution $\delta \upsilon$ . This could be modelled as an uncertainty on the velocity position of each point. Unfortunately the errors on the abscissa are rarely included in non-linear fitting procedures because the system is considerably heavier to solve and because it often prevents convergence. To evaluate the resulting uncertainties on the fit parameters, namely the central opacity, the velocity centroid, and the FWHM, we apply the fitting procedure on 3000 synthetic spectra of FWHM $\Delta \upsilon$ varying between 0.3 and 3.4 km s^-1 sampled with the finite spectral resolution of the observations $\delta \upsilon \sim 0.13$ km s^-1. A noise is added to the x-coordinates of all the spectral points. The rms of all the measured linewidths $\Delta \upsilon'$ is found to scale as

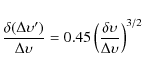
$\begin{displaymath}\frac{\delta (\Delta \upsilon')}{\Delta \upsilon} = 0.45 \left( \frac{\delta \upsilon}{\Delta \upsilon} \right)^{3/2} \end{displaymath}$

(B.1)

and decreases from 0.04 to 0.01 km s^-1 as the true linewidth increases from 0.3 to 3.4 km s^-1. These uncertainties are smaller than (or comparable to) those inferred from the fitting procedure and the resulting errors on the column densities are at most 12%. In comparison the resulting errors on central opacities and velocity centroids are negligible.

Appendix C: Cyanides chemical network

Table C.1: Rates k of the main reactions of the cyanide chemistry.

Figures C.1 and C.2 show the main production and destruction pathways of the hydrogenation chains of carbon, nitrogen, and cyano, resulting from the PDR ( $n_{\rm H} = 50$ cm^-3, A_V = 0.4) and TDR ( $n_{\rm H} = 50$ cm^-3, A_V = 0.4, a = 10^-11 s^-1) models respectively. These figures are simplified: for each species, only the reactions which altogether contribute at least to 70 percent of the total destruction and formation rate are displayed. There is one major difference between these networks: in a UV-dominated chemical model, the cyanide chemistry is initiated by:

$\begin{displaymath}{\rm CH} + {\rm N} \rightarrow {\rm CN} + {\rm H}, \end{displaymath}$

(C.1)

$\begin{displaymath}{\rm CH}_2 + {\rm N} \rightarrow {\rm HCN} + {\rm H}, \end{displaymath}$

(C.2)

and

$\begin{displaymath}{\rm NH} + {\rm C}^{+} \rightarrow {\rm CN}^{+} + {\rm H}; \end{displaymath}$

(C.3)

while in a chemistry driven by turbulent dissipation, the hydrogenation chain of cyano is triggered by the ion-neutral reactions:

$\begin{displaymath}{\rm CH}^{+} + {\rm N} \rightarrow {\rm CN}^{+} + {\rm H}, \end{displaymath}$

(C.4)

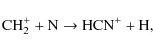
$\begin{displaymath}{\rm CH}_2^{+} + {\rm N} \rightarrow {\rm HCN}^{+} + {\rm H}, \end{displaymath}$

(C.5)

and

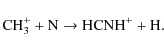
$\begin{displaymath}{\rm CH}_3^{+} + {\rm N} \rightarrow {\rm HCNH}^{+} + {\rm H}. \end{displaymath}$

(C.6)

Since the pathways displayed in Figs. C.1 and C.2 depend on the chemical rates, and since the nitrogen and cyanide chemistry are still poorly known, we list the chemical rates we have adopted in our models for several reactions in Table C.1.

$\begin{figure} \par\includegraphics[width=14cm,clip]{14283-fig8.eps} \end{figure}$	Figure C.1: Chemical network of a UV-dominated chemistry: $n_{\rm H}$ = 50 cm^-3 and A_V = 0.4. This figure is simplified: for each species, only the reactions which altogether contribute at least to 70 percent of the total destruction and formation rate are displayed. The red arrow show the endoenergetic reactions with the energy involved.
Open with DEXTER

$\begin{figure} \includegraphics[width=14cm,clip]{14283-fig9.eps} %\end{figure}$	Figure C.2: Same as Fig. C.1 for a turbulence-dominated chemistry: $n_{\rm H}$ = 50 cm^-3, A_V = 0.4 and a = 10^-11 s^-1. For the sake of simplicity, the main destruction route of N (N + CH₂⁺ $\rightarrow$ HCN⁺ + H) and the main formation pathway of N⁺ (photodissociation of NO⁺) are not displayed here: those two species are therefore highlighted.
Open with DEXTER

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.