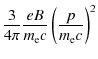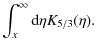| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 18 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/200913450 | |
| Published online | 21 September 2010 | |
Online Material
Appendix A: Modelling
Most of the calculations discussed here are limited to the two-dimensional (2D) plane of the binary orbit. Only in Sect. A.7 do we rotate the results of the 2D calculations into the three-dimensional (3D) simulation volume that is used to calculate the resulting flux.
A.1 Binary orbit
Figure A.1 shows how the
two stars are positioned in the XY plane of the 3D
simulation volume.
The primary is at the centre of the volume
and the position of the secondary is
determined by the orbital phase.
The angle of periastron (![]() )
is measured from
the intersection of the plane of the sky with the
plane of the orbit. The sight-line towards the observer is in the
YZ plane and the inclination angle i is the angle between the
plane of the sky and the orbital plane. The secondary rotates
clockwise in this figure (as seen from above). Periastron
corresponds to phase 0.0.
)
is measured from
the intersection of the plane of the sky with the
plane of the orbit. The sight-line towards the observer is in the
YZ plane and the inclination angle i is the angle between the
plane of the sky and the orbital plane. The secondary rotates
clockwise in this figure (as seen from above). Periastron
corresponds to phase 0.0.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{13450fg10.eps}
\end{figure}](/articles/aa/olm/2010/11/aa13450-09/Timg144.png)
|
Figure A.1:
Binary orbit in the XY
plane of the 3D simulation volume. The primary is positioned at the
centre of the volume. The argument of periastron is denoted |
| Open with DEXTER | |
A.2 Contact discontinuity
The position of the contact discontinuity at any given orbital phase
is determined by the balance of ram pressure between the velocity components
orthogonal to the contact discontinuity (see equations in Antokhin et al. 2004).
These equations take into account that the terminal velocity of the
winds
may not have been reached yet before they collide. Specifically, in the
Cyg OB2 No. 8A standard model presented in Sect. 5.1, the winds collide with
![]() (primary) and
(primary) and
![]() (secondary) at the apex at periastron.
After the stellar wind material has passed through the shock, it
then moves outward parallel to the contact discontinuity (there is also a small orthogonal velocity component, see Sect. A.5).
We assume that the shocks and the contact discontinuity are
sufficiently close to one another that we do not need to make a
distinction in their geometric positions.
On each side of the contact discontinuity, we assume the stellar wind
to have a
(secondary) at the apex at periastron.
After the stellar wind material has passed through the shock, it
then moves outward parallel to the contact discontinuity (there is also a small orthogonal velocity component, see Sect. A.5).
We assume that the shocks and the contact discontinuity are
sufficiently close to one another that we do not need to make a
distinction in their geometric positions.
On each side of the contact discontinuity, we assume the stellar wind
to have a ![]() velocity law and a density derived from
the mass conservation law, using the assumed velocity law
and mass-loss rate.
velocity law and a density derived from
the mass conservation law, using the assumed velocity law
and mass-loss rate.
A.3 Momentum distribution relativistic electrons
We determine the momentum distribution of the relativistic electrons
for a grid of points
along the two shocks. We start with a population of electrons
generated at a given point on the shock itself. We then follow the
time evolution of this population as it advects away and cools down.
The momentum distribution uses a grid that is uniform in
![]() ,
between p0 = 1.0 MeV/c
(for the choice of this specific value, see
Van Loo et al. 2004)
and the upper limit
,
between p0 = 1.0 MeV/c
(for the choice of this specific value, see
Van Loo et al. 2004)
and the upper limit ![]() (defined below, Eq. (A.3))
These limits are sufficiently wide to
cover all of the radio emission we are interested in.
We stop following the electrons when their
momentum falls below p0, or when they leave the simulation
volume. (In our calculations we checked that the
emission beyond the simulation volume is negligible.)
(defined below, Eq. (A.3))
These limits are sufficiently wide to
cover all of the radio emission we are interested in.
We stop following the electrons when their
momentum falls below p0, or when they leave the simulation
volume. (In our calculations we checked that the
emission beyond the simulation volume is negligible.)
In the following, we refer mainly to Van Loo (2005, hereafter VL) as the source for the equations. Citations to the original papers can be found in that reference.
A.4 New relativistic electrons
At the shock, new relativistic electrons are put into the system.
Taking into account the particle acceleration mechanism
and the inverse Compton cooling, it can be shown that
their momenta follow a modified power-law distribution
(VL, Eqs. (5.5), (5.6)):
| N(p) | = | 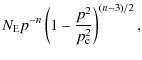
|
(A.1) |
| n | = | (A.2) |
With (VL, Eqs. (5.1)-(3)):
with
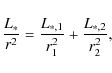
|
(A.4) |
with r1 the distance to the primary and r2 the distance to the secondary. Also (VL, Eq. (3.7)):
| (A.5) |
where u1 is the upstream velocity and u2 the downstream one and the shock strength
The normalization factor ![]() is related to
is related to ![]() ,
the fraction of
energy that gets transferred from the shock to the relativistic particles, by
(VL, Eq. (5.10)):
,
the fraction of
energy that gets transferred from the shock to the relativistic particles, by
(VL, Eq. (5.10)):
where
The magnetic field at distance r to the relevant star is assumed to be given by
(Weber & Davis 1967;
(VL, Eq. (2.48))):
where B* is the surface magnetic field (assumed to be 100 G) and
A.5 Advection and cooling
During a time step ![]() ,
the relativistic electrons advect away and
cool mainly due to inverse Compton and adiabatic cooling (see
Chen 1992; and VL, p. 96,
for a discussion on other cooling mechanisms and why they are not
important in the present situation).
,
the relativistic electrons advect away and
cool mainly due to inverse Compton and adiabatic cooling (see
Chen 1992; and VL, p. 96,
for a discussion on other cooling mechanisms and why they are not
important in the present situation).
The equation for cooling of a single relativistic electron can be written as:
where a p2 gives the inverse Compton
Integration of Eq. (A.8) gives:
where
We will also need the following derivative:
![\begin{displaymath}\frac{{\rm d}p_{\rm init}}{{\rm d}p} = \frac{\exp (-b \Delta ...
...{a}{b} p \left( 1 - \exp (-b \Delta t) \right)\right]^2} \cdot
\end{displaymath}](/articles/aa/olm/2010/11/aa13450-09/img171.png)
|
(A.13) |
We assume that only the momentum p changes significantly with time; for the other variables, we take their value mid-way between the start and the end of the time step
The above equations describe what happens to a single relativistic
electron. The time evolution of the momentum distribution function over
the time step ![]() is:
is:
We stop following the electrons when their momentum falls below p0, or when they leave the simulation volume.
In our simplifying assumptions the contact discontinuity
and the shock are at the same geometrical position. Taken literally, this
would result in a synchrotron emitting region that has zero thickness and
zero synchrotron emission. In the true hydrodynamical situation, particles
move through the shock (which is at some distance from the contact
discontinuity) and then move slowly towards the contact discontinuity.
At the same time, they are being advected outward with a velocity
parallel to the contact discontinuity that is much larger than
the corresponding orthogonal velocity. The thickness of the
synchrotron emitting region is set by the combination of these
two velocities.
In the absence of hydrodynamical information, we use the following
procedure to determine these velocities.
The parallel component (
![]() )
at the contact discontinuity
is determined by
projecting the smooth wind velocity vector on to the contact discontinuity.
At other positions in the wind, we interpolate in the grid of
)
at the contact discontinuity
is determined by
projecting the smooth wind velocity vector on to the contact discontinuity.
At other positions in the wind, we interpolate in the grid of
![]() as a function of the y-coordinate.
The orthogonal component (
as a function of the y-coordinate.
The orthogonal component (
![]() )
at the contact discontinuity is expected to be of the order of
the orthogonal component of the material coming into the shock, with a minimum
value corresponding to the thermal expansion of the gas. As a
simplification, we set it exactly equal to the incoming orthogonal component,
and we use the same type of interpolation
as for the parallel velocity to determine it at other positions.
We reverse the orthogonal velocity direction
to have the gas moving away from the contact discontinuity.
Note that this situation is ``inside out'' compared to the
true hydrodynamical situation where the particles move towards
the contact discontinuity. The thickness of the synchrotron emitting
region is so small however that this inversion has negligible influence on
our results.
)
at the contact discontinuity is expected to be of the order of
the orthogonal component of the material coming into the shock, with a minimum
value corresponding to the thermal expansion of the gas. As a
simplification, we set it exactly equal to the incoming orthogonal component,
and we use the same type of interpolation
as for the parallel velocity to determine it at other positions.
We reverse the orthogonal velocity direction
to have the gas moving away from the contact discontinuity.
Note that this situation is ``inside out'' compared to the
true hydrodynamical situation where the particles move towards
the contact discontinuity. The thickness of the synchrotron emitting
region is so small however that this inversion has negligible influence on
our results.
A.6 Emissivity
The equation for the emissivity is given by (VL, Eq. (B.1)):
with (VL, Eq. (2.51), (2.50)):
We use Eq. (A.7) for the magnetic field. Note that this is an approximation, as the shock may compress the magnetic field as well, leading to higher values than given by Eq. (A.7). The expression for
where
To reduce
the computing time we set
![]() in the
in the
![]() factors of Eq. (A.15) and we also use:
factors of Eq. (A.15) and we also use:
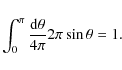
|
(A.21) |
The F function is precalculated on a grid of x-values; the evaluation of the function then reduces to an interpolation.
A.7 Map into 3D grid
Using the equations from the previous sections, we can make a 2D map of the synchrotron emission (part of which is shown in Fig. 6). Note that the synchrotron emission extends on both sides of the contact discontinuity, because there is a shock on either side. Based on the cylindrical symmetry around the line connecting the two stars (at the given orbital phase), we then ``rotate'' this 2D map into the 3D simulation volume.
It is important that during this procedure we do not lose part
of the emission due to interpolation or reduced resolution.
To achieve this, we use volume-integrated emissivities.
While doing the 2D calculation we store the volume integrated
emissivity
![]() defined by:
defined by:
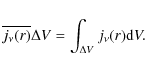
|
(A.22) |
The volume
When we have finished the full 2D calculation,
we rotate the 2D plane into the 3D simulation volume,
using steps of angle ![]() (as defined above).
For each of the emissivity volumes
(as defined above).
For each of the emissivity volumes ![]() defined above, and for
a given rotation angle, we determine
what fraction of the rotated volume overlaps with the
cells in the 3D simulation volume. This is done by
subdividing each dimension of the
defined above, and for
a given rotation angle, we determine
what fraction of the rotated volume overlaps with the
cells in the 3D simulation volume. This is done by
subdividing each dimension of the ![]() volume into three.
For each of the resulting 33 points
we determine in which
3D simulation cell they end up after rotation.
A running sum for that cell is then updated with
the fraction 3-3
of the volume integrated emissivity
volume into three.
For each of the resulting 33 points
we determine in which
3D simulation cell they end up after rotation.
A running sum for that cell is then updated with
the fraction 3-3
of the volume integrated emissivity
![]() of the rotated volume.
At the end of this procedure, the accumulated emission in each
3D simulation cell is divided by its volume, thus obtaining
of the rotated volume.
At the end of this procedure, the accumulated emission in each
3D simulation cell is divided by its volume, thus obtaining
![]() for that cell.
for that cell.
In this procedure we lose some resolution, specifically around the apex, where the 2D resolution is quite high but where the 3D resolution is much lower. However, because of the use of volume-integrated quantities, we do not lose any of the synchrotron emission. Furthermore, the apex of the wind is well hidden by the free-free absorption and will therefore not contribute to the resulting radio flux at the wavelengths we consider. If our model were to be applied to X-rays, optical emission or radio emission at much shorter wavelengths, a higher-resolution 3D grid would be required.
In the 3D model. we also include the thermal free-free opacity and
emissivity, which is due to the ionized wind material.
To calculate
these we use the Wright & Barlow (1975) equations.
The winds of both stars are assumed to be smooth.
For the Gaunt factor at frequency ![]() we use the equation from
Leitherer & Robert (1991):
we use the equation from
Leitherer & Robert (1991):
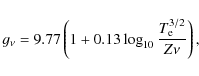
|
(A.23) |
where
Appendix B: Data reduction
The data reduction is accomplished using the Astronomical Image Processing System (AIPS), developed by the NRAO. We follow the standard procedures of antenna gain calibration, absolute flux calibration, imaging and deconvolution. Where possible, we apply self-calibration to the observations (see notes to Table B.1). We measure the fluxes and error bars by fitting elliptical Gaussians to the sources on the images. The error bars listed in Table B.1 include not only the rms noise in the map, but also an estimate of the systematic errors that were evaluated using a jackknife technique. This technique drops part of the observed data and redetermines the fluxes, giving some indication of systematic errors that can be present. Upper limits are three times the uncertainty as derived above. For details of the reduction, we refer to the previous papers in this series (Blomme et al. 2007; Van Loo et al. 2008; Blomme et al. 2005). We exclude from Table B.1 those observations with upper limits higher than 6 mJy (which corresponds to about 3 times the highest detection at all wavelengths).
A comparison with values previously published in the literature
shows that in most cases the error bars overlap with ours.
There are just a few exceptions, which we discuss further.
Bieging et al. (1989) list only an upper limit for the AC116 2 cm observation, while we find
a detection (though marginal at just above 3 sigma). Our detection
is quite consistent in all variants we consider in the jackknife test
and is at the exact position of Cyg OB2 No. 8A, so we consider it a detection.
For the AS483 6 cm, Waldron et al. (1998)
find a value of
![]() mJy, which is
mJy, which is ![]() 20% lower than our value.
A possible explanation is that they did not correct for the
decreasing sensitivity of the primary beam. This effect is
important when the target is not in the centre of the image, and
is approximately 20% for the position of No. 8A on the image.
Puls et al. (2006) list an upper limit of 0.54 mJy for the AS786 6 cm observation,
but we clearly detect Cyg OB2 No. 8A on the image we made.
Bieging et al. (1989) find a slightly lower value of
20% lower than our value.
A possible explanation is that they did not correct for the
decreasing sensitivity of the primary beam. This effect is
important when the target is not in the centre of the image, and
is approximately 20% for the position of No. 8A on the image.
Puls et al. (2006) list an upper limit of 0.54 mJy for the AS786 6 cm observation,
but we clearly detect Cyg OB2 No. 8A on the image we made.
Bieging et al. (1989) find a slightly lower value of
![]() mJy for the
AC116 1984-12-21, 20 cm observation. We have no explanation for these last two discrepancies.
mJy for the
AC116 1984-12-21, 20 cm observation. We have no explanation for these last two discrepancies.
We also take the opportunity to correct some clerical errors in the literature: Bieging et al. (1989) date the CHUR observations as 1980-Mar-22, but it should be 1980-May-23. The Waldron et al. (1998) 1991 observation was made at 3.6 cm, not at 6 cm and the 1992 observation was made in January, not June.
Table B.1: Reduction of the Cyg OB2 No. 8A VLA data.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



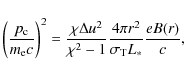
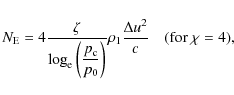
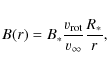
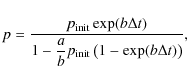
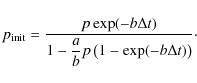
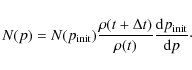
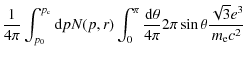
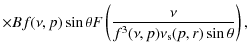
![$\displaystyle \left[ 1+ \frac{\nu_0^2}{\nu^2} \left( \frac{p}{m_{\rm e} c} \right)^2 \right]^{-1/2}$](/articles/aa/olm/2010/11/aa13450-09/img180.png)