EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) A273 Full HTML
Open Access

Table D.1.

Decomposition, of all the power spectra models used in Adams & Blake (2017, 2020), Lai et al. (2022), Carreres et al. (2023), and the one developed in this study.

AB17 (Adams & Blake 2017) - Wide-angle model without RSD on density
Fields ab Term number n wab,n Fab,n 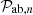P ab , n $ {{\cal {{P}}}_{\mathrm {ab},n}} $
gg 0 (bσ8)2 1 Pmm(k)
gv 0 bσ8fσ8 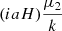( iaH ) μ 2 k $ (iaH) \frac {\mu _2}{k} $ Pmθ(k)Du(k,σu)
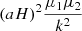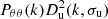vv 0 (fσ8)2 ( aH ) 2 μ 1 μ 2 k 2 $ (aH)^{2} \frac {\mu _1 \mu _2}{k^2} $ P θ θ ( k ) D u 2 ( k , σ u ) $ P_{{\theta \theta }} (k) D_{\mathrm {u}}^2(k,\sigma _{\mathrm {u}}) $
AB20 (Adams & Blake 2020) - Plane-parallel model with RSD on density
Field ab Term n wab,n Fab,n 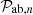P ab , n $ {{\cal {{P}}}_{\mathrm {ab},n}} $
0 (bσ8)2 exp [ − ( k σ g μ ) 2 ] $ \exp \left [-(k\sigma _{\mathrm {g}}\mu )^2\right ] $ Pmm(k)
gg 1 (bσ8)2βf 2 μ 2 exp [ − ( k σ g μ ) 2 ] $ 2 \mu ^2 \exp \left [-(k\sigma _{\mathrm {g}}\mu )^2\right ] $ Pmθ(k)
2 ( b σ 8 ) 2 β f 2 $ (b\sigma _8)^2 \beta _f^2 $ μ 4 exp [ − ( k σ g μ ) 2 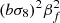] $ \mu ^4 \exp \left [-(k\sigma _{\mathrm {g}}\mu )^2\right ] $ Pθθ(k)
gv 0 bσ8fσ8 ( iaH ) μ k exp [ − ( k σ g μ ) 2 2 ] $ (iaH) \frac {\mu }{k} \exp \left [-\frac {(k \sigma _{\mathrm {g}}\mu )^2}{2}\right ] $ Pmθ(k)Du(k,σu)
1 (fσ8)2 ( iaH ) μ 3 k exp [ − ( k σ g μ ) 2 2 ] $ (iaH)\frac {\mu ^3}{k} \exp \left [-\frac {(k \sigma _{\mathrm {g}}\mu )^2}{2}\right ] $ Pθθ(k)Du(k,σu)
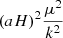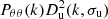vv 0 (fσ8)2 ( aH ) 2 μ 2 k 2 $ (aH)^{2} \frac {\mu ^2}{k^2} $ P θ θ ( k ) D u 2 ( k , σ u ) $ P_{{\theta \theta }} (k) D_{\mathrm {u}}^2(k,\sigma _{\mathrm {u}}) $
L22 (Lai et al. 2022) - Wide-angle model with RSD and Taylor expansion of FoG
Field ab Term n wab,n Fab,n 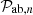P ab , n $ {{\cal {{P}}}_{\mathrm {ab},n}} $
0,m 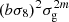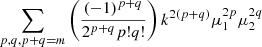( b σ 8 ) 2 σ g 2 m $ (b\sigma _8) ^2 \sigma _{\mathrm {g}}^{2m} $ ∑ p , q , p + q = m ( ( − 1 ) p + q 2 p + q p ! q ! ) k 2 ( p + q ) μ 1 2 p μ 2 2 q $ \sum _{p,q, p+q = m} \left (\frac {(-1)^{p+q}}{2^{p+q} p! q!}\right ) k^{2(p+q)} \mu _1^{2p} \mu _2^{2q} $ Pmm(k)
gg 1,m 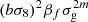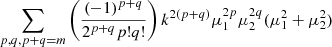( b σ 8 ) 2 β f σ g 2 m $ (b\sigma _8)^2 \beta _f \sigma _{\mathrm {g}}^{2m} $ ∑ p , q , p + q = m ( ( − 1 ) p + q 2 p + q p ! q ! ) k 2 ( p + q ) μ 1 2 p μ 2 2 q ( μ 1 2 + μ 2 2 ) $ \sum _{p,q, p+q = m} \left (\frac {(-1)^{p+q}}{2^{p+q} p! q!}\right ) k^{2(p+q)} \mu _1^{2p} \mu _2^{2q} (\mu _1^{2} + \mu _2^{2}) $ Pmθ(k)
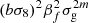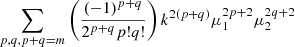2,m ( b σ 8 ) 2 β f 2 σ g 2 m $ (b\sigma _8)^2 \beta _f^2 \sigma _{\mathrm {g}}^{2m} $ ∑ p , q , p + q = m ( ( − 1 ) p + q 2 p + q p ! q ! ) k 2 ( p + q ) μ 1 2 p + 2 μ 2 2 q + 2 $ \sum _{p,q, p+q = m} \left (\frac {(-1)^{p+q}}{2^{p+q} p! q!} \right )k^{2(p+q)} \mu _1^{2p+2} \mu _2^{2q+2} $ Pθθ(k)
gv 0,m 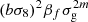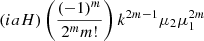( b σ 8 ) 2 β f σ g 2 m $ (b\sigma _8)^2 \beta _f \sigma _{\mathrm {g}}^{2m} $ ( iaH ) ( ( − 1 ) m 2 m m ! ) k 2 m − 1 μ 2 μ 1 2 m $ (iaH) \left (\frac {(-1)^m}{2^m m!}\right ) k^{2m-1} \mu _2 \mu _1^{2m} $ Pmθ(k)Du(k,σu)
1,m 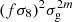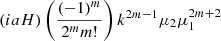( f σ 8 ) 2 σ g 2 m $ (f\sigma _8)^2 \sigma _{\mathrm {g}}^{2m} $ ( iaH ) ( ( − 1 ) m 2 m m ! ) k 2 m − 1 μ 2 μ 1 2 m + 2 $ (iaH) \left (\frac {(-1)^m}{2^m m!}\right ) k^{2m-1} \mu _2 \mu _1^{2m+2} $ Pθθ(k)Du(k,σu)
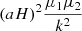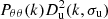vv 0 (fσ8)2 ( aH ) 2 μ 1 μ 2 k 2 $ (aH)^{2} \frac {\mu _1 \mu _2}{k^2} $ P θ θ ( k ) D u 2 ( k , σ u ) $ P_{{\theta \theta }} (k) D_{\mathrm {u}}^2(k,\sigma _{\mathrm {u}}) $
RC25 This study - Wide-angle model with RSD
Field ab Term n wab,n Fab,n 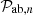P ab , n $ {{\cal {{P}}}_{\mathrm {ab},n}} $
0 (bσ8)2 exp [ − k 2 σ g 2 ( μ 1 2 + μ 2 2 ) 2 ] $ \exp \left [-\frac {k^2 \sigma _{\mathrm {g}}^2 (\mu _1^2 + \mu _2^2)}{2}\right ] $ Pmm(k)
gg 1 (bσ8)2βf ( μ 1 2 + μ 2 2 ) exp [ − k 2 σ g 2 ( μ 1 2 + μ 2 2 ) 2 ] $ (\mu _1^2 + \mu _2^2) \exp \left [-\frac {k^2 \sigma _{\mathrm {g}}^2 (\mu _1^2 + \mu _2^2)}{2}\right ] $ Pmθ(k)
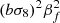2 ( b σ 8 ) 2 β f 2 $ (b\sigma _8)^2 \beta _f^2 $ μ 1 2 μ 2 2 exp [ − k 2 σ g 2 ( μ 1 2 + μ 2 2 ) 2 ] $ \mu _1^2 \mu _2^2 \exp \left [-\frac {k^2 \sigma _{\mathrm {g}}^2 (\mu _1^2 + \mu _2^2)}{2}\right ] $ Pθθ(k)
gv 0 (bσ8)2βf ( iaH ) μ 2 k exp [ − ( k σ g μ 1 ) 2 2 ] $ (iaH) \frac {\mu _2}{k} \exp \left [-\frac {(k \sigma _{\mathrm {g}}\mu _1)^2}{2}\right ] $ Pmθ(k)Du(k,σu)
1 (fσ8)2 ( iaH ) μ 2 μ 1 2 k exp [ − ( k σ g μ 1 ) 2 2 ] $ (iaH) \frac {\mu _2 \mu _1^2}{k} \exp \left [-\frac {(k \sigma _{\mathrm {g}}\mu _1)^2}{2}\right ] $ Pθθ(k)Du(k,σu)
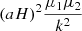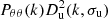vv 0 (fσ8)2 ( aH ) 2 μ 1 μ 2 k 2 $ (aH)^{2} \frac {\mu _1 \mu _2}{k^2} $ P θ θ ( k ) D u 2 ( k , σ u ) $ P_{{\theta \theta }} (k) D_{\mathrm {u}}^2(k,\sigma _{\mathrm {u}}) $

Notes. The decomposition was performed in the flip framework following Eq. 5: The wab,n terms correspond to the model parameters to fit, Fab,n to the geometrical terms that are analytically integrated, and Π to the individual power spectrum terms that are numerically integrated. For the case of Carreres et al. (2023) model which included only velocity covariance, the vv terms corresponds to the one of AB17, L22, and RC25. In addition to all previously defined terms, we define the galaxy bias b, the RSD parameter βf=f/b, the RSD FoG parameter σg, and the velocity position FoG parameter, σu. For the L22, we grouped the gg terms with index p and q which have the same sum m=p+q. The m index is run for each term depending on the maximal term in the Taylor expansion (i.e., p and q for gg, and m for gv).

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.