Generalized framework for likelihood-based field-level inference of growth rate from velocity and density fields

Open Access

Table 1.

Velocity redshift dependence implemented in flip to convert Hubble diagram residuals into peculiar velocities.

Name	Watkins	Low-z	Hubble high-order	Full
p_i	z_obs,i	z_obs,i	z_obs,i, q₀, j₀	z_obs,i,D(z_obs,i), H(z_obs,i)/h

J(p_i)	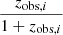$\frac{z_{obs, i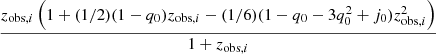}}{1 + z_{obs, i}}$ $\frac {z_{\mathrm {obs},i}}{1+z_{\mathrm {obs},i}}$	z_obs,i	$\frac{z_{obs, i} (1 + (1 / 2) (1 - q_{0}) z_{obs, i} - (1 / 6) (1 - q_{0} - 3 q_{0}^{2} + j_{0}) z_{obs, i}^{2})}{1 + z_{obs, i}}$ $\frac {z_{\mathrm {obs},i} \left (1 + (1/2) (1 - q_0) z_{\mathrm {obs},i} - (1/6) (1 - q_0 - 3 q_0^2 + j_0) z_{\mathrm {obs},i}^2\right )}{1+z_{\mathrm {obs},i}}$	${(\frac{(1 + z_{obs, i}) c}{(H (z_{obs, i}) / h) D (z_{obs, i})} - 1)}^{- 1}$ $\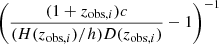left (\frac {(1+z_{\mathrm {obs},i})c}{(H(z_{\mathrm {obs},i})/h) D(z_{\mathrm {obs},i})} - 1 \right )^{-1}$

Notes. In addition to the terms defined in the text, the q₀ and j₀ parameters are, respectively, the deceleration and jerk parameters in the higher-order development of the Hubble law.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.