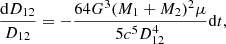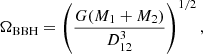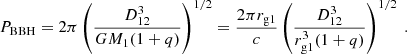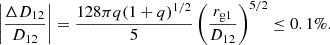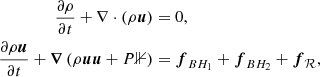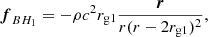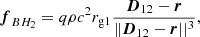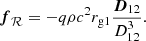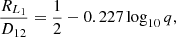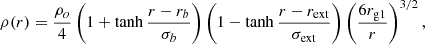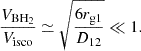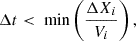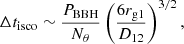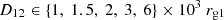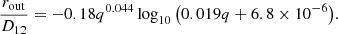EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) A59 Full HTML
Open Access
Issue
A&A
Volume 698, May 2025
Article Number A59
Number of page(s) 10
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202453586
Published online 28 May 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

For more than three decades, binary black hole (BBH) systems have remained an astrophysical conjecture in the context of colliding galaxies hosting supermassive black holes (SMBHs, Begelman et al. 1980). In that scenario, SMBHs are expected to bind gravitationally and to progressively get closer until they merge. In recent years, numerous studies have been performed to understand the physical processes behind this in-spiral motion. For orbital separations beyond the parsec scale, the dynamical friction of black holes with the galactic gaseous environment appears to be the dominant process (Mayer et al. 2007). At orbital separations below 10−2 pc, gravitational wave emission is expected to be the key phenomenon driving the in-spiral motion until the fusion of the two compact objects. Between these two separation scales no clear consensus has emerged identifying the mechanism driving the in-spiral motion, known as the ‘final parsec problem’. The current candidates for driving this process include three-body stellar interaction (see e.g. Preto et al. 2011) and disc gas interaction (e.g. Armitage & Natarajan 2002; Cuadra et al. 2009).

Since the first detection of gravitational waves emitted by the fusion of a stellar BBH (Abbott et al. 2016), the BBH conjecture has become a vivid reality in the astrophysical community. Such a discovery has enhanced the relevance of numerical studies devoted to the structure of the binary system, including the interaction between the two compact objects and the circumbinary disc (CBD) surrounding them (MacFadyen & Milosavljević 2008; Ragusa et al. 2016; Muñoz et al. 2020; Siwek et al. 2023; Franchini et al. 2023), the impact of the binary gravitational field upon the CBD (Noble et al. 2012; Zilhão et al. 2015; Noble et al. 2021; Mignon-Risse et al. 2023a), the presence of individual accretion structures around each black hole (also dubbed ‘mini-discs’) (Pihajoki et al. 2018; Ingram et al. 2021; Davelaar & Haiman 2022), or the existence of the so-called lump structure at the inner edge of the CBD (Shi et al. 2012; Noble et al. 2012; D’Orazio et al. 2013; Mignon-Risse et al. 2023b).

Understanding the dynamical structure of the gas orbiting within the complex gravitational field generated by the BBH is likely to be a key to discriminate between single black holes and pre-merger BBHs through the electromagnetic output of the system. So far, the characterisation of electromagnetic signatures of BBH systems have been performed in the framework of black hole orbital separations of up to a few hundreds of gravitational radii (see, e.g. Tanaka et al. 2012; Tang et al. 2018; d’Ascoli et al. 2018; Combi et al. 2022; Krauth et al. 2024; Cocchiararo et al. 2024). Such studies have suggested that the electromagnetic BBH signature should be detectable for most of the mass ratio of the BBH, provided the redshift of these systems remains relatively small. It is noteworthy that all the aforementioned studies have been performed assuming ad hoc initial conditions that do not originate from simulations devoted to earlier phases of the binary (see e.g. Lai & Muñoz 2023 for a review on general binaries and Duffell et al. 2024 for a review on numerical simulations devoted to supermassive BBHs). Specifically, it remains unclear how the CBD formed around the BBH, thus leading to uncertainties regarding initial conditions used in fluid simulations and the derived electromagnetic emission of the binary in the CBD stage. Simulations of the early phase of the binary (i.e. before the formation of the CBD) are then required to bridge the gap between the very early stage (pre-CBD) and the CBD stage of the binary system. The transition between these two stages of BBH systems is not yet clearly identified in terms of black hole separation. However since no active galactic nuclei (AGNs) exhibit accretion discs whose outer radii are larger a few thousands of gravitational radii of the central black hole (see e.g. Jha et al. 2022, and references therein), it is likely that CBDs do not extend to more than a few thousand gravitational radii. As such, the separation between the two black holes in the CBD stage is likely to be of the order of (at most) a few hundred gravitational radii. Regarding pre-CBD BBH, the separation between the two black holes can be quite large – and even larger than the typical size of AGN discs. Thus, we can assume that in the pre-CBD stage, one or even two of the black holes are still surrounded by their own ‘primordial’ accretion discs.

Pre-CBD BBH exhibit gravitational fields that are quite similar to other binary systems, such as binary stars or star-planet systems. In a classical gravitational context, numerous authors have already investigated the impact of the presence of a bound gravitational disruptor upon the accretion disc surrounding a central star or planet. Among the various particularities of these discs, various studies have agreed on the assumption that the radial extent of the disc is limited well below the Roche lobe size. Such a result was obtained using various approaches, including testing particles on periodic orbits (Paczynski 1977; Eggleton 1983; Pichardo et al. 2005), applying perturbation theory to hydrodynamical disc equilibrium (Papaloizou & Pringle 1977; Artymowicz & Lubow 1994; Miranda & Lai 2015), or using smoothed-particle hydrodynamics simulations (Artymowicz & Lubow 1994; Martin & Lubow 2011). Regarding the internal structure of individual disc, the presence of the secondary object is likely to induce spiral waves propagating in the disc surrounding the primary black hole, as shown by Sawada et al. (1986) and Spruit (1987). Other studies have been performed in various astrophysical contexts, whose results support the existence of such waves for instance in cataclysmic variables (Godon et al. 1998; Ju et al. 2016), protoplanetary discs (Rafikov 2016; Bae & Zhu 2018), circumplanetary discs (Zhu et al. 2016), and in mini-discs formed around the components of BBH systems (Ryan & MacFadyen 2017). Finally, the gravitational influence of the secondary component of the binary system is also believed to affect the outer edge of the disc orbiting the primary component leading to an elliptical shape (Whitehurst & King 1991; Lubow 1994; Quillen et al. 2005; Westernacher-Schneider et al. 2024). Based on the aforementioned studies and the similarities regarding gravitational fields, we would expect similar features to also appear in individual accretion discs orbiting black holes in pre-CBD BBH systems.

The goal of the present paper is to make a first step to bridging pre-CBD systems and BBH systems in the CBD stage by studying the gravitational impact of a secondary black hole upon an accretion disc orbiting around a primary black hole, while assuming both black holes to be gravitationally bound. The existence of such link would help discriminate among BBH candidates and could potentially lead to the identification of pre-CBD BBH systems. The aim of such simulations is to assess if it is possible to link the characteristics of the disc surrounding the primary black hole (i.e. its observables) with the parameters of the binary (i.e. its separation and mass ratio). Such detections would be invaluable as they would provide observational clues to the gas structure throughout the evolution of the binary and thus to the formation of the CBD.

Section 2 is devoted to the numerical framework and set-up of simulations of a large accretion disc surrounding a primary black hole (hereafter dubbed as the circumprimary disc) and prone to the gravitational influence of a secondary black hole orbiting beyond the outer edge of the accretion disc. Section 3 presents the results of equal-mass BBH hydrodynamical simulations while Sect. 4 generalises the results to unequal mass BBH systems. The last section summarises the results and discusses the perspectives of our work.

2. Hydrodynamic simulations of accretion discs in early BBH systems

In this paper, we aim to study the effects of the presence of an external gravitational disruptor upon the accretion disc orbiting around a black hole. As we focus our study on the early phase of the BBH, namely, when the distance between the black hole and the secondary object, D12, is much larger than the size of the black hole gravitational radius rg1 = GM1/c2. In this expression, G stands for the gravitational constant, while c is the velocity of light. The other key parameter describing the BBH is obviously the mass ratio of the two black holes, which we define as q = M2/M1, with M1 indicating the heavier of the black holes.

2.1. Early stage of circular orbiting BBH: Pre-CBD stage

The two black holes composing the BBH system are gravitationally bound and orbit around the center of mass of the system. Many studies focussing on the impact of mass and angular momentum transfer between the CBD and the binary have found that the trajectories of the two objects display an eccentricity, whose values range between 0.3 and 0.8; the only exception is if they are initially close to a circular orbit (Armitage & Natarajan 2005; Cuadra et al. 2009; Roedig et al. 2011; Muñoz et al. 2019; Zrake et al. 2021). Such a result is valid in the context of a BBH surrounded by a CBD and does not include the momentum loss driven by the emission of gravitational waves. For earlier systems (i.e. pre-CBD BBH), no firm constraint has yet been put on the motion of the two black holes; thus, we chose the simplest configuration possible, namely, having both black holes moving on circular orbits around the centre of mass of the BBH on the same plane as the circumprimary accretion disc.

If we assume that the loss of angular momentum in the binary is mainly induced by the emission of gravitational waves, the variation of the orbital separation of the binary D12 occurring over a timescale dt is provided by (Hughes 2009):

d D 12 D 12 = − 64 G 3 ( M 1 + M 2 ) 2 μ 5 c 5 D 12 4 d t , $$ \begin{aligned} \frac{\mathrm{d}D_{12}}{D_{12}}=-\frac{64G^3(M_1+M_2)^2\mu }{5c^5D_{12}^4}\mathrm{d}t ,\end{aligned} $$(1)

where μ = M1M2/(M1 + M2). In a circular orbit configuration, the angular frequency of the BBH is given by

Ω BBH = ( G ( M 1 + M 2 ) D 12 3 ) 1 / 2 , $$ \begin{aligned} \Omega _{\rm BBH} = \left(\frac{G(M_1+M_2)}{D_{12}^3}\right)^{1/2} ,\end{aligned} $$(2)

where the distances of each object from the centre of mass of the system are r1 = qD12/(q + 1) and r2 = D12/(q + 1), respectively. The velocity of both the black hole and the secondary object in the frame of the centre of mass of the system will then be β12 = V12/c2 = qrg1/D12 and β22 = rg1/D12. Early stages of the BBH will then lead to black hole velocities much smaller than the velocity of light, thus opening the way to a classical description of the motion of both black holes. In the remainder of this paper, we use the orbital period of the BBH as time reference, namely,

P BBH = 2 π ( D 12 3 G M 1 ( 1 + q ) ) 1 / 2 = 2 π r g 1 c ( D 12 3 r g 1 3 ( 1 + q ) ) 1 / 2 . $$ \begin{aligned} P_{\rm BBH} = 2\pi \left(\frac{D^3_{12}}{GM_1(1+q)}\right)^{1/2}=\frac{2\pi r_{\rm g1}}{c}\left(\frac{D^3_{12}}{r^3_{\rm g1}(1+q)}\right)^{1/2} \ . \end{aligned} $$(3)

To fulfill the circular orbit assumption made in this paper, we have to first check that the shrinking of the binary separation is limited over one binary period; for instance, |ΔD12/D12|≤0.1% for Δt = PBBH. The previous equations then lead to a lower limit of the binary separation D12, namely,

| Δ D 12 D 12 | = 128 π q ( 1 + q ) 1 / 2 5 ( r g 1 D 12 ) 5 / 2 ≤ 0.1 % . $$ \begin{aligned} \left|\frac{\Delta D_{12}}{D_{12}}\right| = \frac{128\pi q(1+q)^{1/2}}{5}\left(\frac{r_{\rm g1}}{D_{12}}\right)^{5/2}\le 0.1\% .\end{aligned} $$(4)

This is verified if D12 ≥ 100 rg1. To stay well outside of the CBD forming phase, we decided to restrict our investigation to separations D12 ≥ 500 rg1 to ensure that the BBH system is in the pre-CBD phase; in addition, this allows us to safely assume that the in-spiral motion due to gravitational wave emission is negligible over a very large number of BBH periods. This is of prime interest as the follow up of the evolution of the accretion disc prone to an external orbiting massive object requires us to perform simulations of the fluid into the complex gravitational field generated by the presence of the two massive objects over a very long time (i.e. up to a thousand binary periods).

While the secondary black hole is probably surrounded by its own accretion disc, the gravitational influence this disc would have upon the circumprimary disc is likely negligible compared to the effect we are studying here, so we did neglect this force in our simulations. Also, we did not include the secondary black hole and its accretion disc in our computational domain, as we chose to focus on the circumprimary disc; this is because it is likely to be the most visible gas structure in the BBH, as we set the primary black hole to be the most massive object of the binary (q ≤ 1). In our study, we thus considered two parameters of the system as free: the binary separation, D12, and the black hole mass ratio of q ≤ 1. Altogether, these two free parameters characterise the gravitational influence of the secondary black hole upon the circumprimary accretion disc provided the orbits of the black holes are circular. The parameters for the various simulations performed in this study are listed in Table 1.

Table 1.

BBH mass ratio q and black hole separation D12 for our set of hydrodynamical simulations.

2.2. Hydrodynamics simulations of the accretion disc around black hole in BBH

2.2.1. Simulation framework

The best framework for performing our simulations coincides with the primary black hole, as it is possible to ensure in that frame the numerical conservation of the angular momentum of the gas (this frame is referred to as ℛ hereafter). In such a frame, the centre of mass of the accretion disc remains at a constant distance from the primary black hole; but we still have to consider fictitious forces at work upon the fluid. The framework associated with the primary black hole does have a circular motion around the centre of mass of the BBH system. In the Cartesian framework associated with the center of mass, we chose to keep the axis of ℛ parallel to the axis of the inertial frame of the centre of mass of the system. This ensures that the frame ℛ is not rotating, so no Coriolis forces have to be accounted for in this frame. As a result, the secondary black hole will also experience a circular motion in ℛ, whose radius and angular velocity are D12 and ΩBBH, respectively.

Within our set of simulations, we aim to describe the long-term evolution of the entire disc orbiting around the primary black hole. To do so, we needed to include the whole extent of the disc from the innermost stable circular orbit (ISCO) to the external radius of the disc. As the gravity of the primary black hole closely matches Newtonian gravity beyond 20 rg1, we chose to use a classical hydrodynamics framework. This choice enables us to keep good accuracy in our description of the disc while optimising the computing time. Moreover, encompassing the gravitational effects of the secondary black hole then becomes much easier, as its influence is of Newtonian nature (as would any massive object at such distance).

In their earliest phase, BBH systems are slow evolving, so the approach of the two black holes and the mutual gravitational interaction is very likely to align the accretion disc’s spin with the plane hosting the motion of the black holes. Accordingly, here we consider 2D simulations within that plane (see e.g. Liska et al. 2021). To take into account the relativistic nature of the primary black hole, we use the pseudo-Newtonian description provided by Paczynsky & Wiita (1980), so that the inner edge of the disc forms near the ISCO. We chose this description based on our aim of studying the global behavior of the disc, with an emphasis on its outer parts where the spin of the primary black hole is likely to have a negligible impact.

2.2.2. Hydrodynamics equations

The set of hydrodynamics equations translates the conservation of mass and momentum of the gas in the complex gravitational field of the BBH system. These conservation laws is expressed:

∂ ρ ∂ t + ∇ · ( ρ u ) = 0 , ∂ ρ u ∂ t + ∇ ( ρ u u + P 1 ) = f B H 1 + f B H 2 + f R , $$ \begin{aligned} \frac{\partial \rho }{\partial t} + \nabla \cdot (\rho \boldsymbol{u})&= 0, \nonumber \\ \frac{\partial \rho \boldsymbol{u}}{\partial t} + \boldsymbol{\nabla }\left(\rho \boldsymbol{u}\boldsymbol{u} + P\mathbb{1} \right)&= {\boldsymbol{f}}_{BH_1}+{\boldsymbol{f}}_{BH_2}+ {\boldsymbol{f}}_\mathcal{{R}} ,\end{aligned} $$(5)

where ρ is the gas density, ρu is the gas momentum density, P is the thermal pressure, and 𝟙 is the identity matrix. The momentum conservation law takes into account the gravitational force densities generated by the central black hole using a pseudo-Newtonian prescription of the force of the central black hole:

f B H 1 = − ρ c 2 r g 1 r r ( r − 2 r g 1 ) 2 , $$ \begin{aligned} {\boldsymbol{f}}_{BH_1} = -\rho c^2r_{\rm g1}\frac{\boldsymbol{r}}{r(r-2r_{\rm g1})^2} ,\end{aligned} $$(6)

where r is the position vector of a given gas element in the frame of the central black hole where ∥r∥=r. The gravitational force density originating from the secondary black hole, fBH2, orbiting around the primary one in the ℛ frame can be described with very good accuracy by a Newtonian law, as the distance between any element of gas and the secondary black hole remains large compared to the gravitational radius, rg2, of the second black hole. This force is expressed:

f B H 2 = q ρ c 2 r g 1 D 12 − r ‖ D 12 − r | | 3 , $$ \begin{aligned} {\boldsymbol{f}}_{BH_2} = q\rho c^2r_{\rm g1}\frac{{\boldsymbol{D}}_{12}-\boldsymbol{r}}{\Vert {\boldsymbol{D}}_{12}-\boldsymbol{r}||^3} ,\end{aligned} $$(7)

where D12 is the position vector of the second black hole in the frame of the central black hole; namely, the ℛ frame. In addition to these two gravitational force densities, we also has to consider the fictitious forces due to the rotation of ℛ. As already mentioned, the orientation of the axis of the ℛ frame remains constant, so no Coriolis force has to be considered and the only fictitious force is then:

f R = − q ρ c 2 r g 1 D 12 D 12 3 . $$ \begin{aligned} {\boldsymbol{f}}_\mathcal{{R}} = - q\rho c^2r_{\rm g1}\frac{{\boldsymbol{D}}_{12}}{D_{12}^3} .\end{aligned} $$(8)

To close the set of equations, we used a polytropic equation of state, providing the value of the thermal pressure, P, as a function of the density, namely, P = κργ with γ = 5/3 and κ = 10−4. The value of γ is chosen in agreement with monoatomic gas characteristics.

2.2.3. Numerical simulation set-up

The goal of this paper is to study the impact of the gravitational influence of a secondary black hole upon the circumprimary disc. In contrast to single black hole systems, the presence of a second black hole in the BBH system likely impacts the outer edge to the accretion disc of the primary black hole. To quantify that effect, we set up hydrodynamic simulations solving the aforementioned equations in the 2D orbital plane. The simulation domain is designed to encompass the entire accretion disc from its inner to its outer edges. The simulation domain is thus set to be ϕ ∈ [0, 2π] and r ∈ [5rg1, 0.98D12], so that this domain contains the inner edge of the accretion disc while maintaining velocities below the speed of light. The radius, RL1, of the L1 Lagrangian point of the BBH system is approximately (Plavec & Kratochvil 1964; Hameury 2001):

R L 1 D 12 = 1 2 − 0.227 log 10 q , $$ \begin{aligned} \frac{R_{L_1}}{D_{12}} =\frac{1}{2} - 0.227\log _{10} q ,\end{aligned} $$(9)

so that it lies within our simulation domain for any mass ratio q ≥ 7 × 10−3. The location of the L1 Lagrangian point of the system being a helpful indicator of the upper limit of the outer radius of an accretion disc in a binary system; thus, we could make sure that the evolution of the outer edge of the accretion disc will be captured by our simulation.

The initial conditions of the simulations are consistent with the balance of an accretion disc prone to the gravitational field of a single non-spinning black hole; namely, with an inner edge located near the innermost stable circular orbit (ISCO), with risco = 6rg1 and an outer edge located close to the outer limit of the simulation domain. The initial gas density is prescribed as

ρ ( r ) = ρ o 4 ( 1 + tanh r − r b σ b ) ( 1 − tanh r − r ext σ ext ) ( 6 r g 1 r ) 3 / 2 , $$ \begin{aligned} \rho (r) = \frac{\rho _o}{4}\left(1+\tanh {\frac{r-r_b}{\sigma _b}}\right)\left(1-\tanh {\frac{r-r_{\rm ext}}{\sigma _{\rm ext}}}\right)\left(\frac{6r_{\rm g1}}{r}\right)^{3/2} ,\end{aligned} $$(10)

where ρo = 10, rb = 9rg1 and rext = 0.7D12 (see Vincent et al. 2013). The two constants, σb and σext, have been set to 0.9rg1 and 0.05D12, respectively, for the disc to exhibit edges. At this point, the density drops to a floor value of ρmin, which is ten orders of magnitude smaller than the maximal initial density value. Radial velocity is set to zero initially and the azimuthal velocity is computed in order for the gas to reach a full balance between the central black hole gravitational field, the centrifugal force and the thermal pressure of the gas. We chose the value of the parameter κ in the polytropic equation of state to be κ = 10−4 to mimic the physics of a thin accretion disc. This parameter is indeed directly connected to the disc sound speed and to the disc scale height, h, through the vertical hydrostatic equilibrium of the disc. According to the initial disc density, the pressure in the disc is consistent with a constant disc aspect ratio, h/r ∼ 0.07.

The challenge of these simulations stems from the fact that there is a huge contrast between the dynamical timescale of the gas lying at risco and the timescale related to the orbit of the secondary black hole. The ratio of these timescales is indeed proportional to the ratio of the velocity of the secondary black hole to the velocity of the gas at risco, namely,

V BH 2 V isco ≃ 6 r g 1 D 12 ≪ 1 . $$ \begin{aligned} \frac{V_{\rm BH_2}}{V_{\rm isco}} \simeq \sqrt{\frac{6r_{\rm g1}}{D_{12}}}\ll 1 .\end{aligned} $$(11)

We should also highlight the fact that the spatial resolution needed to accurately describe the dynamics of the gas requires much smaller cells near the inner edge than at the outer edge of the simulation. To alleviate the numerical cost of these simulations, we use a logarithmically radially spaced grid with Nr = 720 cells in the radial direction and Nθ = 320 in the azimuthal one. The use of a logarithmic grid is an important asset to perform these simulations, but cannot prevent us from considering a huge numerical cost for these simulations. Indeed, the time step of hydrodynamics simulations is controlled by the so-called Courant-Friedrish-Levy (CFL) condition translating the causality of hydrodynamical phenomena as

Δ t < min ( Δ X i V i ) , $$ \begin{aligned} \Delta t < \text{ min}\left(\frac{\Delta X_i}{V_i}\right) ,\end{aligned} $$(12)

where ΔXi is the size of a cell in the ith direction. The dominant velocity component of the gas in the accretion disc being the azimuthal one (with velocity is close to the Keplerian speed), the previous condition leads to a simulation time step

Δ t isco ∼ P BBH N θ ( 6 r g 1 D 12 ) 3 / 2 , $$ \begin{aligned} \Delta t_{\rm isco} \sim \frac{P_{\rm BBH}}{N_{\theta }}\left(\frac{6r_{\rm g1}}{D_{12}}\right)^{3/2} ,\end{aligned} $$(13)

where Nθ = 320 is the azimuthal resolution of the grid. As we wish to follow the evolution of the whole accretion in pre-CBD binaries whose separations are up to 6 × 103rg1, the previous relation indicates that we have to perform up to 107 hydrodynamical iterations per BBH period, PBBH. As an example, the number of iterations required to perform our most remote BBH configuration is near ten billion time steps.

Regarding the boundaries of the computational domain, we opted for periodic boundary conditions in the azimuthal direction, while outflowing conditions were imposed at the inner radial boundary. At the outer radial boundary of the simulation, we did not prevent gas from entering the computational domain as this can lead to unphysical effects such as an artificial thermal pressure gradient. Instead, we allow gas to inflow into the computational domain with a density very close to the floor density. This is especially valid as the outer edge of the disc stays well inside the grid while cells near the outer boundary are mimicking the ambient medium outside the disc. We have displayed on Fig. 1 an illustration of the outer boundary conditions: matter reaching the outer boundary can exit the domain (outer oriented arrows), while entering mass (inner oriented arrows) is set to a density much lower than the one from the disc.

thumbnail Fig. 1.

Illustration of the outer boundary conditions imposed on the computational domain with the color map representing the density, while arrows show the sign of the radial velocity of the matter in the outer part of the computational domain at a time: t = 0.29PBBH. On the one hand, the gas is allowed to exit the computational domain without modifying its density; whereas on the other hand, the inflowing gas can enter the computational domain with a density set to a value very close to the density floor. Such conditions are designed to mimic the ambient medium standing outside of the disc and to prevent any artificial input of gas from the exterior of the domain.

The numerical set-up presented in this section has been used identically in all simulations displayed in this study. The entire set-up is only dependent on the two BBH parameters, namely, the separation, D12, between the two black holes and the mass ratio, q. As we express all physical quantities using the two aforementioned parameters, we can then scan the range values of these parameters while ensuring an identical initial set-up.

3. Impact of the binary separation on the circumprimary disc of an equal-mass BBH

To study how the presence of a secondary black hole impacts the circumprimary disc we chose to first focus on exploring how the separation between the two black holes impacts the circumprimary disc in the case of an equal mass pre-circumbinary BBH (q = 1) configuration, where we expect the most striking consequences.

3.1. Sculpting the outer edge of a circumprimary disc in an equal-mass BBH: Fiducial case

We first present the fiducial case of a separation D12 = 2 × 103rg1, which is well above the threshold for our circular orbit hypothesis defined in Eq. (4), but also large enough so that no circumbinary structure exists yet. The design of our simulations, presented in the previous section, is consistent with an initial accretion disc whose extent exceeds the size of the Roche lobe of the primary black hole.

The temporal evolution of the gas density is displayed on Fig. 2, where one can see the outer part of the initial disc being swept away by the gravitational force exerted by the secondary black hole located outside of the simulation domain. The transition from the initial conditions to the shrunken accretion disc lasts for approximately one BBH period, before stepping into a stabilisation phase, where the accretion disc slowly rearranges itself under the influence of the two black holes.

thumbnail Fig. 2.

Snapshots of the logarithmic density of an accretion disc surrounding the primary black hole of a pre-CBD BBH. The secondary black hole orbiting in a circular motion around the primary black hole (in the frame of the primary black hole) has an equal mass (q = 1), while being separated by D12 = 2000 rg1. Time here is normalised to the BBH period PBBH. The tidal effects induced by the presence of the secondary object leads to the removal of the outer part of the initial disc whose outer edge lies beyond the Lagrangian L1 point of the BBH. After more than one orbital period of the BBH, the disc remains stable with an outer edge reduced to approximately 600 rg1, while displaying an elliptic outer edge shape whose eccentricity is e = 0.52 ± 0.12.

It is noteworthy that the gravitational influence of the secondary black hole upon the circumprimary disc is also noticeable through the formation of overdense spiral arms. The outer parts of these arms rotate at the same angular velocity than the secondary black hole near the outer edge of the disc, but experience the differential rotation of the gas as they progress through the inner part of the disc. The differential rotation of the gas leads to a spiral shape of the arms. The presence of these over-densities remains, however, throughout the whole simulation, but in a more rolled-up fashion, making the spiral arms more prominent in the very inner part of the circumprimary disc.

Lastly, we followed the disc evolution for more than 20 periods of the binary and we see in the last frame of Fig. 2 that the shrunken outer edge of the disc is not circular anymore, but it shows eccentricity following the orbit of the secondary black hole.

3.1.1. Assessing the outer radius of a circumprimary disc

During the accretion disc evolution, precisely assessing the value of its outer edge is not straightforward since the shape of the outer edge evolves toward an elliptic structure. It is, however, useful to measure the azimuthally averaged outer radius in order to follow its evolution and final value under the presence of the secondary black hole. To do so, we adopted the following procedure to measure the radial extent of the disc for any given snapshot. First, we must azimuthally average the gas density of the disc so that we can obtain its averaged radial profile. This profile is displayed on the top of Fig. 3 for our fiducial simulation, where both the initial and final profiles are represented.

thumbnail Fig. 3.

Comparison of the initial radial profiles of the density (upper panel) and azimuthal velocity (lower panel) of the disc with final profiles of the simulation. The profiles are obtained by azimuthally averaging the corresponding snapshots.

We can see that the density profile has evolved over time since the gas density has increased inside the disc; whereas it has significantly dropped beyond a reference point where both the initial and final densities match. We used this reference point to define the average outer edge of the disc rout, which corresponds to the radius where the gas density is equal to one tenth of the density at the reference point. This choice is motivated by the fact that a 90% drop in the disc density results in a drop in thermal radiative emission power by a factor larger than 90%, depending on the gas equation of state. Such a drop in thermal emission will be detectable compared to an extended disc and will be observationally interpreted as the outer accretion disc’s edge. It is noteworthy that the azimuthally averaged azimuthal velocity (shown in the bottom panel of Fig. 3) remains very similar to the Keplerian velocity up to a radius close to the outer radius chosen with the method above. This is consistent with the gas no longer displaying the dynamical behavior of a balanced disc structure. Outside of rout, mass is very likely reacting to equivalent gravitational forces coming from the two objects composing the BBH.

3.1.2. Evolution of the outer radius of the circumprimary disc

Applying this method to determine rout to our fiducial simulation leads us to Fig. 4, where the temporal evolution of rout is displayed over nearly 25 PBBH. In such simulation, the initial disc whose outer edge lies at rout = 1500 rg1 (beyond the Roche lobe radius of the primary black hole) rapidly shrinks to a smaller extension, which remains stationary after approximately 3PBBH. The final outer edge radius of the disc in this simulation is then ≃600 rg1.

thumbnail Fig. 4.

Temporal evolution of the averaged outer radius of the disc displayed in Fig. 2. Time is normalised to the binary period, PBBH. After a fast decrease from the initial outer edge value (1.55 × 103rg1), the outer edge radius stabilises to a value of approximately 600 rg1.

The general behavior of rout in this fiducial simulation matches the overall behavior of the disc in all our other simulations: a rapid decrease in the outer edge followed by a stabilisation of the outer edge. To understand why the disc is experiencing such rapid shrinking in this simulation, we have to keep in mind that PBBH is large, compared to the gas dynamical time, as PBBH corresponds to four orbiting periods of the gas near rout and 6 × 103 periods at the ISCO of the disc.

3.1.3. Eccentricity of the outer edge of the circumprimary disc

As we see in Fig. 2, the final shape of the outer edge of the circumprimary disc no longer exhibits an axisymmetric structure, as the outer edge of the accretion disc appears to be elliptical. Inferring the eccentricity of the outer part of the resulting disc was done using the following procedure. First, we calculated the contour of the gas density, ρ, in the outer disc (where values of the density are much smaller than unity but larger than the floor density). In a second step, we removed the spiral arms from this contour and finally we evaluated the approximation of this contour by an ellipse. The fitting algorithm is built from algebraic equations of an ellipse. All elliptical fits were obtained from the object-oriented tools for fitting conics and quadrics developed by Matt (2023) within the Maple library.

For our fiducial case, displayed in Fig. 2, we obtained a final eccentricity for the outer edge of the disc of e = 0.52 ± 0.12 (see Fig. 5). The error bars were computed by carrying out the above procedure several times for different close parameters. This case has the largest error bar of all our simulations.

thumbnail Fig. 5.

Snapshot of the logarithmic density of the fiducial simulation (Fig. 2, where q = 1 and D12 = 2 × 103rg1) at the final stable stage. We added a black solid line to indicate the location of the outer edge of the disc and a white solid line representing the elliptic fit of this outer edge, whose eccentricity is e = 0.52 ± 0.12.

3.2. Extension to all separations for equal-mass binary

To see how the outer edge of the disc behaves depending on the separation, we performed other equal-mass BBH simulations considering various separations,

D 12 ∈ { 1 , 1.5 , 2 , 3 , 6 } × 10 3 r g 1 $$ D_{12}\in \{ 1, \ 1.5, \ 2, \ 3, \ 6\} \times 10^3\ r_{\rm g1} $$

which translate into physical separations between [0.48,  2.9]×10−4(M1/106 M⊙)pc. In all those simulations, we obtained a similar behavior to the one displayed in Fig. 4, where we show the evolution of rout as a function of time.

To compare the outer edges of the circum-primary disc (even though all the systems have different separations), we normalised each outer edge radius by the respective separation of their binary. As we can see in Fig. 6, the evolution of rout/D12 is not only very similar throughout our equal-mass BBH sample, with a rapid drop in the outer radius occurring over a few PBBH, but they also all converge towards a final value of rout ≃ (0.3 ± 0.015)D12. This outcome was not unexpected, as the dynamical aspect of the equal mass binary system scales with the distance. We also computed the eccentricity associated with those different equal-mass BBHs and found that they are all coherent with 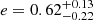e = 0 . 62 − 0.22 + 0.13 $ e= 0.62^{+0.13}_{-0.22} $.

thumbnail Fig. 6.

Temporal evolution of the outer edge of accretion discs in equal-mass binaries whose separation range from 500 rg1 to 6 × 103rg1. The outer radius of the disc is normalised to the binary separation, while the time is normalised to the binary period PBBH.

The results from the equal-mass BBH simulations suggest that the binary separation has little to no impact on the values of rout/D12 and the eccentricity of the outer edge. To investigate whether the BBH mass ratio, q, has a significant impact on those quantities, we need to allow the mass ratio to change and see how that impacts the overall behavior of the outer edge and its eccentricity.

4. Accretion disc’s outer edge in a pre-CBD BBH: Non-equal-mass binaries versus the separation

To go beyond the equal-mass BBH framework, we performed a series of simulations, where we considered six different BBH mass ratios, q, and six separations, D12, to get a good representation of the parameter space and see how the outer radius behaves for all cases. The range of mass ratios considered in our simulation sample is q ∈ [9 × 10−4, 1]. The lower value of this interval was constrained by computational time limitations, while we set the upper limit to q = 1, as we ran the simulation around the most massive black-hole.

The range of binary separation in our sample is D12/rg1 ∈ [500, 6 × 103]. The upper limit of the black hole separation corresponds to an accretion disc whose initial outer edge is consistent with a typical size of accretion discs observed around SMBHs (see e.g. Jha et al. 2022 and references therein). The lower limit corresponds to a set-up where it is numerically possible to address simulations with very low mass ratio, q, down to ∼10−3. At such low values of q, we do have to perform long-term simulations over nearly one thousand BBH periods for the disc to reach an equilibrium state. Such long-term simulations are then easier to perform if the separation is small but still larger than the limit for the circular orbit condition (Eq. (4)) and coherent with a pre-CBD BBH.

4.1. Measurement of the outer radius of circumprimary discs in non-equal mass pre-CBD BBH

For each simulation listed in Table 1 we measured the outer edge of the accretion disc in the exact same way than in Sect. 3.1.1 and compiled the results in order to study the relationship between rout and the two BBH parameters, q and D12. Figure 7 represents the value of the ratio rout/D12 as a function of the mass ratio parameter, q. The main result provided by this figure is that the ratios rout/D12 are remarkably similar for any given mass ratio q. For any given mass ratio, the final outer edge radius in each simulation is indeed equal to the same fraction of D12, whatever the BBH separation D12. Scanning the various values of the BBH mass ratio, we find that this fraction is, however, dependent on q, as its value increases as q decreases. To check the consistency of our simulations, we represent in Fig. 7 the distance from the primary black hole to the L1 Lagrange point of the BBH system, as well as the location of the inner Lindblad resonance. All the values of rout found in our sample are smaller than these two distances proving the stability of the final structure of the accretion flow around the primary black hole of the BBH. At high mass ratios, the location of the L1 is the main limitation, while at low mass ratios, the Lindblad inner resonance is dominating the extent of the circumprimary disc. We provide here an empirical formula, represented by the dash line on Fig. 7, that fits the results arising from our simulations as:

r out D 12 = − 0.18 q 0.044 log 10 ( 0.019 q + 6.8 × 10 − 6 ) . $$ \begin{aligned} \frac{r_{\rm out}}{D_{12}} = -0.18q^{0.044}\log _{10}{\left(0.019q+6.8\times 10^{-6}\right)} .\end{aligned} $$(14)

thumbnail Fig. 7.

Ratio of the average disc outer radius rout to the BBH separation D12 as a function of the BBH mass ratio q. The colored points correspond to various BBH separations. For any given BBH mass ratio, the values of rout/D12 are very close for all separations showing that this ratio does only depend on the BBH mass ratio, q. We can also notice that all values of rout are smaller than both the size of the Roche lobe (Eggleton 1983) and the location of the innermost Lindblad resonance as expected for any stable accretion disc.

The coefficients of this formula were derived by minimising a standard χ2 test based on the values provided by our simulations (with a χ2 = 0.99 and residues below 1%). From Eq. 14, we see that the outer radius of the circumprimary disc stays proportional to binary separation, with the proportionality factor only depending on the mass ratio. This means that the outer radius of the circumprimary disc is a reliable indicator of the binary separation during the pre-CBD phase of the inspiral. When comparing our results with Pichardo et al. (2005), we find a general agreement in terms of mass ratio dependance while obtaining marginally larger outer radii. We interpret that slight difference to originate from different definitions of the outer radius: it is defined from the outermost non-intersecting test-particle loop at the binary periastron in Pichardo et al. (2005), while we computed an average value of the outer radius based on the drop of the thermal emissivity from the disc.

The result presented here, linking any evolution of the outer edge of the disc with a decrease in separation, is interesting not only as a test for all the existing BBH candidates, but also to look for new potential candidates. This relation does indeed emphasise the need to question any AGN system exhibiting evidence of an accretion disc with a smaller outer radius than expected. In our sample, we covered three orders of magnitude for the q parameter which leads to rout ∈ {0.3,  0.6}D12. Taking those numbers into account provides a location range for the search of the potential secondary black hole at the origin of this shaved outer disc.

4.2. Eccentricity of the outer edge of a circumprimary disc in non equal-mass pre-CBD BBH

Following the same technique presented in Sect. 3.1, we looked at the eccentricity of the outer edge of the circumprimary disc in all our simulations. The results obtained from the fitting of the shape of the outer edge of the circumprimary disc are displayed on Fig. 8, along with the associated uncertainties. As expected we can see that for the smallest values of the mass ratio, q, the eccentricity, e, is small and increases with q. On the other hand we find that for the mass ratio q > 10−2, the outer edge of the disc exhibits a high eccentricity of e ∼ 0.6, as can be seen in the final snapshots of Fig. 2 and in Fig. 5. As a result, the outer disc eccentricity cannot be used as a potential tracer of the mass ratio for q < 10−2. Moreover, we also need to keep in mind that we focused on black hole orbits without any eccentricity of their own. Using a purely newtonian 2D hydrodynamical approach, Quillen et al. (2005) showed that increasing the eccentricity of the gravitational disruptor tends to form a more circular looking outer edge of the disc; however, no precise study of the outer edge eccentricity was performed. If such effects would also apply to BBHs, it would mean that a non-detection of eccentricity in the outer disc could be the result of an eccentric binary and not only a small mass ratio. Nevertheless, if through other means (e.g. a gravitational wave detection), we could have access to the binary eccentricity, then the shape of the outer disc could further help us discriminate between low and high mass ratios.

thumbnail Fig. 8.

Eccentricity of the outer disc as a function of the binary mass ratio, q. The eccentricity mostly depends on the binary mass ratio parameter, q, and very slightly on the binary separation, D12.

5. Conclusions

In this paper, we consider BBH systems in the pre-circumbinary stage, where the separation between the two black holes can be larger than the typical size of AGN discs. We thus assumed that during this pre-CBD stage, the most massive black hole may still be surrounded by a pre-existing accretion disc dubbed as the circumprimary disc. We have studied how the presence of a gravitationally bound secondary black hole impacts the evolution of the circumprimary disc in a BBH system with the aim to explore whether any characteristic features of this disc could be linked with the binary parameters, thus offering the potential to help identify BBHs. In this first step, we chose to focus on systems whose orbital separations are large (up to a few thousands gravitational radii) enough so that they correspond to the pre-CBD disc BBH stage. This choice was motivated by the fact that it is a relatively unstudied stage of pre-merger systems that rules over the formation of the circumbinary disc prior to the merger phase. Describing such an early stage of the BBH is one of the keys to accurately picture the evolution of BBH systems. In pre-CBD systems, the black-hole inspiral motion is very slow, so it enables us to consider the two black holes moving on circular orbits, while keeping their separation constant.

To link the circumprimary disc characteristics with the binary parameters, we performed a series of 2D hydrodynamical simulations for six separations covering the pre-CBD BBH stage and six mass ratios ranging over three orders of magnitude. Since this study is focussed on the outer edge of the circumprimary disc, we performed those simulations in a classical, pseudo-Newtonian, framework that allowed us to follow the system from more than twenty orbits of the binary for the largest separation to almost a thousand for the closest separation. In each simulation, we reached a stable state with the overall size and shape of the outer circumprimary disc remaining constant (see Fig. 6). This allowed us to use the end result of those simulations as an ‘instantaneous snapshot’ of a pre-CBD system with a given separation (i.e. at a given time of the merger).

We found that the presence of a secondary black hole has three main effects upon the circumprimary accretion disc, similar to previous studies performed on other type of binary systems:

The presence of a smaller than expected disc around a SMBH is not specific to the presence of a gravitational disruptor in the system. This could indeed be related to a gas-poor environment preventing the black-hole from having an extended disc which could be inferred from other observations of the region or it could have been truncated by a fly-by (an unbound massive object); in that case, the resulting outer radius would not only be different, but the secondary object could be detectable as well (Quillen et al. 2005). Hence, while it is not unique to pre-CBD BBHs, the existence of a truncated accretion disc around a SMBH can be considered a flag indicating the need to further study the source to test for a potential binary companion.

This is of particular interest as McHardy et al. (2023) recently published the ‘first detection of the outer edge of an AGN accretion disc’ in NGC 4395. If a gravitationally bound secondary black hole is responsible for such small accretion disc, our results predict a separation of two black holes to range from 1.7 to 3.3 times the outer radius of the accretion disc, provided 10−3 ≤ q ≤ 1. Assessing the detectability of these features is not in the scope of this paper. We refer to our companion paper devoted to the observational implications of the findings of the present work.

Acknowledgments

The numerical simulations we have presented in this paper were produced on the DANTE platform (AstroParticule & Cosmologie, France). Part of this study was supported by the LabEx UnivEarthS, ANR-10-LABX-0023 and ANR-18-IDEX-0001. The data that support the findings of this study are available from the corresponding author, FC, upon request.

References

  1. Abbott, B. P., LIGO Scientific Collaboration,& Virgo Collaboration 2016, Phys. Rev. Lett., 116, 061102 [CrossRef] [PubMed] [Google Scholar]
  2. Armitage, P. J., & Natarajan, P. 2002, ApJ, 567, L9 [NASA ADS] [CrossRef] [Google Scholar]
  3. Armitage, P. J., & Natarajan, P. 2005, ApJ, 634, 921 [NASA ADS] [CrossRef] [Google Scholar]
  4. Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
  5. Bae, J., & Zhu, Z. 2018, ApJ, 859, 118 [Google Scholar]
  6. Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [Google Scholar]
  7. Cocchiararo, F., Franchini, A., Lupi, A., & Sesana, A. 2024, A&A, 691, A250 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Combi, L., Lopez Armengol, F. G., Campanelli, M., et al. 2022, ApJ, 928, 187 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cuadra, J., Armitage, P. J., Alexander, R. D., & Begelman, M. C. 2009, MNRAS, 393, 1423 [Google Scholar]
  10. d’Ascoli, S., Noble, S. C., Bowen, D. B., et al. 2018, ApJ, 865, 140 [CrossRef] [Google Scholar]
  11. Davelaar, J., & Haiman, Z. 2022, Phys. Rev. D, 105, 103010 [NASA ADS] [CrossRef] [Google Scholar]
  12. D’Orazio, D. J., Haiman, Z., & MacFadyen, A. 2013, MNRAS, 436, 2997 [Google Scholar]
  13. Duffell, P. C., Dittmann, A. J., D’Orazio, D. J., et al. 2024, ApJ, 970, 156 [NASA ADS] [CrossRef] [Google Scholar]
  14. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  15. Franchini, A., Lupi, A., Sesana, A., & Haiman, Z. 2023, MNRAS, 522, 1569 [NASA ADS] [CrossRef] [Google Scholar]
  16. Godon, P., Livio, M., & Lubow, S. 1998, MNRAS, 295, L11 [Google Scholar]
  17. Hameury, J.-M. 2001, Ecole de Goutelas, 23, 57 [Google Scholar]
  18. Hughes, S. A. 2009, Am. Astron. Soc. Meeting Abstr., 213, 230.01 [Google Scholar]
  19. Ingram, A., Motta, S. E., Aigrain, S., & Karastergiou, A. 2021, MNRAS, 503, 1703 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jha, V. K., Joshi, R., Chand, H., et al. 2022, MNRAS, 511, 3005 [NASA ADS] [CrossRef] [Google Scholar]
  21. Ju, W., Stone, J. M., & Zhu, Z. 2016, ApJ, 823, 81 [NASA ADS] [CrossRef] [Google Scholar]
  22. Krauth, L. M., Davelaar, J., Haiman, Z., et al. 2024, Phys. Rev. D, 109, 103014 [Google Scholar]
  23. Lai, D., & Muñoz, D. J. 2023, ARA&A, 61, 517 [NASA ADS] [CrossRef] [Google Scholar]
  24. Liska, M., Hesp, C., Tchekhovskoy, A., et al. 2021, MNRAS, 507, 983 [NASA ADS] [CrossRef] [Google Scholar]
  25. Lubow, S. H. 1994, ApJ, 432, 224 [Google Scholar]
  26. MacFadyen, A. I., & Milosavljević, M. 2008, ApJ, 672, 83 [Google Scholar]
  27. Martin, R. G., & Lubow, S. H. 2011, MNRAS, 413, 1447 [Google Scholar]
  28. Matt, J. 2023, Object-oriented tools for fitting conics and quadrics, MATLAB Central File Exchange https://www.mathworks.com/matlabcentral/fileexchange/87584-object-oriented-tools-for-fitting-conics-and-quadrics [Google Scholar]
  29. Mayer, L., Kazantzidis, S., Madau, P., et al. 2007, Science, 316, 1874 [NASA ADS] [CrossRef] [Google Scholar]
  30. McHardy, I. M., Beard, M., Breedt, E., et al. 2023, MNRAS, 519, 3366 [Google Scholar]
  31. Mignon-Risse, R., Varniere, P., & Casse, F. 2023a, MNRAS, 519, 2848 [Google Scholar]
  32. Mignon-Risse, R., Varniere, P., & Casse, F. 2023b, MNRAS, 520, 1285 [NASA ADS] [CrossRef] [Google Scholar]
  33. Miranda, R., & Lai, D. 2015, MNRAS, 452, 2396 [Google Scholar]
  34. Muñoz, D. J., Miranda, R., & Lai, D. 2019, ApJ, 871, 84 [CrossRef] [Google Scholar]
  35. Muñoz, D. J., Lai, D., Kratter, K., & Miranda, R. 2020, ApJ, 889, 114 [Google Scholar]
  36. Noble, S. C., Mundim, B. C., Nakano, H., et al. 2012, ApJ, 755, 51 [NASA ADS] [CrossRef] [Google Scholar]
  37. Noble, S. C., Krolik, J. H., Campanelli, M., et al. 2021, ApJ, 922, 175 [NASA ADS] [CrossRef] [Google Scholar]
  38. Paczynski, B. 1977, ApJ, 216, 822 [CrossRef] [Google Scholar]
  39. Paczynsky, B., & Wiita, P. J. 1980, A&A, 88, 23 [Google Scholar]
  40. Papaloizou, J., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
  41. Pichardo, B., Sparke, L. S., & Aguilar, L. A. 2005, MNRAS, 359, 521 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pihajoki, P., Mannerkoski, M., Nättilä, J., & Johansson, P. H. 2018, ApJ, 863, 8 [Google Scholar]
  43. Plavec, M., & Kratochvil, P. 1964, Bull. Astron. Inst. Czechoslovakia, 15, 165 [NASA ADS] [Google Scholar]
  44. Preto, M., Berentzen, I., Berczik, P., & Spurzem, R. 2011, ApJ, 732, L26 [Google Scholar]
  45. Quillen, A. C., Varnière, P., Minchev, I., & Frank, A. 2005, AJ, 129, 2481 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rafikov, R. R. 2016, ApJ, 831, 122 [NASA ADS] [CrossRef] [Google Scholar]
  47. Ragusa, E., Lodato, G., & Price, D. J. 2016, MNRAS, 460, 1243 [CrossRef] [Google Scholar]
  48. Roedig, C., Dotti, M., Sesana, A., Cuadra, J., & Colpi, M. 2011, MNRAS, 415, 3033 [NASA ADS] [CrossRef] [Google Scholar]
  49. Ryan, G., & MacFadyen, A. 2017, ApJ, 835, 199 [Google Scholar]
  50. Sawada, K., Matsuda, T., & Hachisu, I. 1986, MNRAS, 221, 679 [NASA ADS] [CrossRef] [Google Scholar]
  51. Shi, J.-M., Krolik, J. H., Lubow, S. H., & Hawley, J. F. 2012, ApJ, 749, 118 [Google Scholar]
  52. Siwek, M., Weinberger, R., & Hernquist, L. 2023, MNRAS, 522, 2707 [NASA ADS] [CrossRef] [Google Scholar]
  53. Spruit, H. C. 1987, A&A, 184, 173 [NASA ADS] [Google Scholar]
  54. Tanaka, T., Perna, R., & Haiman, Z. 2012, MNRAS, 425, 2974 [CrossRef] [Google Scholar]
  55. Tang, Y., Haiman, Z., & MacFadyen, A. 2018, MNRAS, 476, 2249 [NASA ADS] [CrossRef] [Google Scholar]
  56. Vincent, F. H., Meheut, H., Varniere, P., & Paumard, T. 2013, A&A, 551, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Westernacher-Schneider, J. R., Zrake, J., MacFadyen, A., & Haiman, Z. 2024, ApJ, 962, 76 [NASA ADS] [CrossRef] [Google Scholar]
  58. Whitehurst, R., & King, A. 1991, MNRAS, 249, 25 [NASA ADS] [CrossRef] [Google Scholar]
  59. Zhu, Z., Ju, W., & Stone, J. M. 2016, ApJ, 832, 193 [CrossRef] [Google Scholar]
  60. Zilhão, M., Noble, S. C., Campanelli, M., & Zlochower, Y. 2015, Phys. Rev. D, 91, 024034 [Google Scholar]
  61. Zrake, J., Tiede, C., MacFadyen, A., & Haiman, Z. 2021, ApJ, 909, L13 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

BBH mass ratio q and black hole separation D12 for our set of hydrodynamical simulations.

In the text

All Figures

thumbnail Fig. 1.

Illustration of the outer boundary conditions imposed on the computational domain with the color map representing the density, while arrows show the sign of the radial velocity of the matter in the outer part of the computational domain at a time: t = 0.29PBBH. On the one hand, the gas is allowed to exit the computational domain without modifying its density; whereas on the other hand, the inflowing gas can enter the computational domain with a density set to a value very close to the density floor. Such conditions are designed to mimic the ambient medium standing outside of the disc and to prevent any artificial input of gas from the exterior of the domain.
In the text
thumbnail Fig. 2.

Snapshots of the logarithmic density of an accretion disc surrounding the primary black hole of a pre-CBD BBH. The secondary black hole orbiting in a circular motion around the primary black hole (in the frame of the primary black hole) has an equal mass (q = 1), while being separated by D12 = 2000 rg1. Time here is normalised to the BBH period PBBH. The tidal effects induced by the presence of the secondary object leads to the removal of the outer part of the initial disc whose outer edge lies beyond the Lagrangian L1 point of the BBH. After more than one orbital period of the BBH, the disc remains stable with an outer edge reduced to approximately 600 rg1, while displaying an elliptic outer edge shape whose eccentricity is e = 0.52 ± 0.12.
In the text
thumbnail Fig. 3.

Comparison of the initial radial profiles of the density (upper panel) and azimuthal velocity (lower panel) of the disc with final profiles of the simulation. The profiles are obtained by azimuthally averaging the corresponding snapshots.
In the text
thumbnail Fig. 4.

Temporal evolution of the averaged outer radius of the disc displayed in Fig. 2. Time is normalised to the binary period, PBBH. After a fast decrease from the initial outer edge value (1.55 × 103rg1), the outer edge radius stabilises to a value of approximately 600 rg1.
In the text
thumbnail Fig. 5.

Snapshot of the logarithmic density of the fiducial simulation (Fig. 2, where q = 1 and D12 = 2 × 103rg1) at the final stable stage. We added a black solid line to indicate the location of the outer edge of the disc and a white solid line representing the elliptic fit of this outer edge, whose eccentricity is e = 0.52 ± 0.12.
In the text
thumbnail Fig. 6.

Temporal evolution of the outer edge of accretion discs in equal-mass binaries whose separation range from 500 rg1 to 6 × 103rg1. The outer radius of the disc is normalised to the binary separation, while the time is normalised to the binary period PBBH.
In the text
thumbnail Fig. 7.

Ratio of the average disc outer radius rout to the BBH separation D12 as a function of the BBH mass ratio q. The colored points correspond to various BBH separations. For any given BBH mass ratio, the values of rout/D12 are very close for all separations showing that this ratio does only depend on the BBH mass ratio, q. We can also notice that all values of rout are smaller than both the size of the Roche lobe (Eggleton 1983) and the location of the innermost Lindblad resonance as expected for any stable accretion disc.
In the text
thumbnail Fig. 8.

Eccentricity of the outer disc as a function of the binary mass ratio, q. The eccentricity mostly depends on the binary mass ratio parameter, q, and very slightly on the binary separation, D12.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.