Selection of optically variable active galactic nuclei via a random forest algorithm

Open Access

Table 3.

List of the bivariate features used in this work grouped under the families introduced in Sect. 3.2 (Tschopp & Hernandez-Rivera 2017).

Minkowski family
City_Block, L₁-norm	d_City = ∑\|g_i − r_i\|
Euclidean, L₂-norm	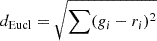$d_{Eucl} = \sqrt{\sum {(g_{i} - r_{i})}^{2}}$ $d_{\text{Eucl}}=\sqrt{\sum(g_i - r_i)^2}$
Chebyshev, L_∞-norm	d_Cv = max_i\|g_i − r_i\|

L₁ family

Sørensen	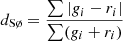$d_{Sø} = \frac{\sum \| g_{i} - r_{i} \|}{\sum (g_{i} + r_{i})}$ $d_{\text{S}{\o}}=\frac{\sum\|g_i - r_i\|}{\sum(g_i + r_i)}$
Gower	d_Gw = ∑\|g_i − r_i\|/b
Kulczynski	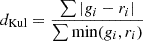$d_{Kul} = \frac{\sum \| g_{i} - r_{i} \|}{\sum min (g_{i}, r_{i})}$ $d_{\text{Kul}}=\frac{\sum\|g_i - r_i\|}{\sum\min(g_i,r_i)}$
Canberra	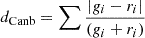$d_{Canb} = \sum \frac{\| g_{i} - r_{i} \|}{(g_{i} + r_{i})}$ $d_{\text{Canb}}=\sum{\frac{\|g_i - r_i\|}{(g_i + r_i)}}$
Lorentzian	d_Lor = ∑ln(1 + \|g_i − r_i\|)

Intersection family

Intersection	d_Is = ∑\|g_i − r_i\|/2
Wave_Hedges	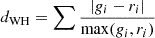$d_{WH} = \sum \frac{\| g_{i} - r_{i} \|}{max (g_{i}, r_{i})}$ $d_{\text{WH}}=\sum{\frac{\|g_i - r_i\|}{\max(g_i,r_i)}}$
Motyka	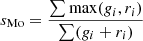$s_{Mo} = \frac{\sum max (g_{i}, r_{i})}{\sum (g_{i} + r_{i})}$ $s_{\text{Mo}}=\frac{\sum\max(g_i,r_i)}{\sum(g_i + r_i)}$
Czekanowski	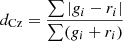$d_{Cz} = \frac{\sum \| g_{i} - r_{i} \|}{\sum (g_{i} + r_{i})}$ $d_{\text{Cz}}=\frac{\sum\|g_i-r_i\|}{\sum(g_i + r_i)}$
Ruzicka	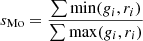$s_{Mo} = \frac{\sum min (g_{i}, r_{i})}{\sum max (g_{i}, r_{i})}$ $s_{\text{Mo}}=\frac{\sum\min(g_i,r_i)}{\sum\max(g_i,r_i)}$

Inner product family

Inner_Product	s_Ip = ∑g_ir_i
Harmonic_Mean	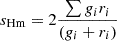$s_{Hm} = 2 \frac{\sum g_{i} r_{i}}{(g_{i} + r_{i})}$ $s_{\text{Hm}} = 2\frac{\sum g_i r_i}{(g_i + r_i)}$
Cosine	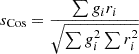$s_{Cos} = \frac{\sum g_{i} r_{i}}{\sqrt{\sum g_{i}^{2} \sum r_{i}^{2}}}$ $s_{\text{Cos}}=\frac{\sum g_i r_i}{\sqrt{\sum g_i^2\sum r_i^2}}$
Jaccard	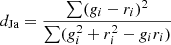$d_{Ja} = \frac{\sum {(g_{i} - r_{i})}^{2}}{\sum (g_{i}^{2} + r_{i}^{2} - g_{i} r_{i})}$ $d_{\text{Ja}}=\frac{\sum(g_i - r_i)^2}{\sum(g_i^2 + r_i^2 - g_i r_i)}$
Dice	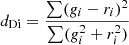$d_{Di} = \frac{\sum {(g_{i} - r_{i})}^{2}}{\sum (g_{i}^{2} + r_{i}^{2})}$ $d_{\text{Di}}=\frac{\sum(g_i - r_i)^2}{\sum(g_i^2 + r_i^2)}$

Fidelity family

Fidelity	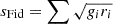$s_{Fid} = \sum \sqrt{g_{i} r_{i}}$ $s_{\text{Fid}}=\sum\sqrt{g_i r_i}$
Bhattacharyya	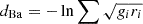$d_{Ba} = - ln \sum \sqrt{g_{i} r_{i}}$ $d_{\text{Ba}}=-\ln\sum\sqrt{g_i r_i}$
Squared-chord	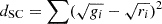$d_{SC} = \sum {(\sqrt{g_{i}} - \sqrt{r_{i}})}^{2}$ $d_{\text{SC}}=\sum(\sqrt{g_i}-\sqrt{r_i})^2$
χ² family
Squared_Euclidean	d_SE = ∑(g_i − r_i)²
Pearson χ²	d_Pea = ∑(g_i − r_i)²/r_i
Neyman χ²	d_Ney = ∑(g_i − r_i)²/g_i
χ²	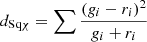$d_{Sq χ} = \sum \frac{{(g_{i} - r_{i})}^{2}}{g_{i} + r_{i}}$ $d_{\text{Sq}\chi}=\sum\frac{(g_i - r_i)^2}{g_i + r_i}$
Divergence	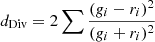$d_{Div} = 2 \sum \frac{{(g_{i} - r_{i})}^{2}}{{(g_{i} + r_{i})}^{2}}$ $d_{\text{Div}} = 2\sum\frac{(g_i - r_i)^2}{(g_i + r_i)^2}$
Clark	$d_{Cl} = \sqrt{\sum {[\frac{\| g_{i} - r_{i} \|}{(g_{i} + r_{i})}]}^{2}}$ $d_{\text{Cl}}= \sqrt{\sum\left[\frac{\|g_i - r_i\|}{(g_i + r_i)}\right]^2}$
Additive_Symmetric χ²	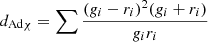$d_{Ad χ} = \sum \frac{{(g_{i} - r_{i})}^{2} (g_{i} + r_{i})}{g_{i} r_{i}}$ $d_{\text{Ad}\chi}= \sum\frac{(g_i - r_i)^2(g_i + r_i)}{g_i r_i}$

Shannon’s entropy family

Kullback-Leibler	d_KL = ∑g_iln(g_i/r_i)
Jeffreys	d_Jef = ∑(g_i − r_i)ln(g_i/r_i)
K-divergence	d_Kdv = ∑g_iln(2g_i/(g_i + r_i))
Topsøe	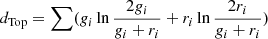$d_{Top} = \sum (g_{i} ln \frac{2 g_{i}}{g_{i} + r_{i}} + r_{i} ln \frac{2 r_{i}}{g_{i} + r_{i}})$ $d_{\text{Top}}=\sum (g_i \ln\frac{2g_i}{g_i + r_i}+r_i \ln\frac{2r_i}{g_i + r_i})$
	−(g_i + r_i)/2 * ln((g_i + r_i)/2))

Combination family

Taneja	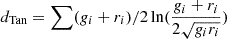$d_{Tan} = \sum (g_{i} + r_{i}) / 2 ln (\frac{g_{i} + r_{i}}{2 \sqrt{g_{i} r_{i}}})$ $d_{\text{Tan}}=\sum (g_i + r_i)/2\ln(\frac{g_i + r_i}{2\sqrt{g_i r_i}})$
Kumar-Johnson	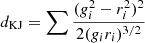$d_{KJ} = \sum \frac{{(g_{i}^{2} - r_{i}^{2})}^{2}}{2 {(g_{i} r_{i})}^{3 / 2}}$ $d_{\text{KJ}}=\sum \frac{(g_i^2 - r_i^2)^2}{2(g_i r_i)^{3/2}}$
Average(L₁-L_∞)	d_avL = ∑(\|g_i − r_i\|+max_i\|g_i − r_i\|)/2

Vicissitude family

Vicis-Wave_Hedges	d_{V_wh} = ∑\|g_i − r_i\|/min(g_i, r_i)
Vicis-Symmetric χ₃²	d_vsχ₃² = ∑(g_i − r_i)²/max(g_i, r_i)
Max-Symmetric χ²	d_MaxS = max(∑(g_i − r_i)²/g_i, ∑(g_i − r_i)²/r_i)
Min-Symmetric χ²	d_MinS = min(∑(g_i − r_i)²/g_i, ∑(g_i − r_i)²/r_i)

Notes. The functions used to compute distance or similarity measures require vectors X and Y (in this case, the g- and r-band light curves) and return the corresponding similarities or distances per the various measures given above.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.