Joint inference of the Milky Way’s star formation history and initial mass function from Gaia all-sky G < 13 data

Home

All issues

Volume 697 (May 2025)

A&A, 697 (2025) A128

Full HTML

Open Access

Table 2

Outputs from the BGM FASt inference for the four runs made up to magnitude G < 13 (‘G13’) considering PARSEC or STAREVOL as stellar evolution model (‘P’ or ‘S’), and fixing or fitting the thick disc SFH (therefore fitting ‘13’ or ‘17’ parameters).

Parameter	Mass/age range	MS	${\bar{θ}}_{G13P-13}$ ${\bar \theta _{{\rm{G13P - 13}}}}$	${\bar{θ}}_{G13S-13}$ ${\bar \theta _{{\rm{G13S - 13}}}}$	${\bar{θ}}_{G13P-17}$ ${\bar \theta _{{\rm{G13P - 17}}}}$	${\bar{θ}}_{G13S-17}$ ${\bar \theta _{{\rm{G13S - 17}}}}$	Units
α₁	0.015–0.5	1.0	(1.0)	(1.0)	(1.0)	(1.0)	Dimensionless
α₂	0.5–1.53	1.7	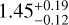${1.45}_{- 0.12}^{+ 0.19}$ $1.45^{+0.19}_{-0.12}$	${2.48}_{- 0.11}^{+ 0.09}$ $2.48_{ - 0.11}^{ + 0.09}$	${1.32}_{- 0.13}^{+ 0.22}$ $1.32_{ - 0.13}^{ + 0.22}$	${2.52}_{- 0.13}^{+ 0.11}$ $2.52_{ - 0.13}^{ + 0.11}$	Dimensionless
α₃	0.53–120	2.4	${1.98}_{- 0.05}^{+ 0.13}$ $1.98_{ - 0.05}^{ + 0.13}$	${1.64}_{- 0.02}^{+ 0.15}$ $1.64_{ - 0.02}^{ + 0.15}$	${2.02}_{- 0.05}^{+ 0.12}$ $2.02_{ - 0.05}^{ + 0.12}$	${1.80}_{- 0.03}^{+ 0.12}$ $1.80_{ - 0.03}^{ + 0.12}$	Dimensionless
$Σ_{⊙}^{0}$ $\Sigma _ \odot ^0$	0−0.15	1.6	${1.10}_{- 0.16}^{+ 0.16}$ $1.10_{ - 0.16}^{ + 0.16}$	${2.26}_{- 0.30}^{+ 0.18}$ $2.26_{ - 0.30}^{ + 0.18}$	${1.04}_{- 0.16}^{+ 0.19}$ $1.04_{ - 0.16}^{ + 0.19}$	${2.06}_{- 0.23}^{+ 0.27}$ $2.06_{ - 0.23}^{ + 0.27}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{1}$ $\Sigma _ \odot ^1$	0.15−1	2.5	${0.55}_{- 0.11}^{+ 0.08}$ $0.55_{ - 0.11}^{ + 0.08}$	${1.69}_{- 0.33}^{+ 0.18}$ $1.69_{ - 0.33}^{ + 0.18}$	${0.51}_{- 0.10}^{+ 0.09}$ $0.51_{ - 0.10}^{ + 0.09}$	${1.35}_{- 0.23}^{+ 0.16}$ $1.35_{ - 0.23}^{ + 0.16}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }{\rm{p}}{{\rm{c}}^{ - 2}}{\rm{Gy}}{{\rm{r}}^{ - 1}}$
$Σ_{⊙}^{2}$ $\Sigma _ \odot ^2$	1−2	2.1	${2.53}_{- 0.45}^{+ 0.27}$ $2.53_{ - 0.45}^{ + 0.27}$	${7.95}_{- 1.73}^{+ 0.75}$ $7.95_{ - 1.73}^{ + 0.75}$	${2.35}_{- 0.36}^{+ 0.32}$ $2.35_{ - 0.36}^{ + 0.32}$	${6.00}_{- 0.99}^{+ 0.66}$ $6.00_{ - 0.99}^{ + 0.66}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{3}$ $\Sigma _ \odot ^3$	2−3	1.7	${3.42}_{- 0.73}^{+ 0.61}$ $3.42_{ - 0.73}^{ + 0.61}$	${7.05}_{- 1.80}^{+ 1.11}$ $7.05_{ - 1.80}^{ + 1.11}$	${3.13}_{- 0.65}^{+ 0.65}$ $3.13_{ - 0.65}^{ + 0.65}$	${5.01}_{- 1.22}^{+ 1.15}$ $5.01_{ - 1.22}^{ + 1.15}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{4}$ $\Sigma _ \odot ^4$	3−4	1.8	${4.70}_{- 1.69}^{+ 1.22}$ $4.70_{ - 1.69}^{ + 1.22}$	${7.61}_{- 1.58}^{+ 2.31}$ $7.61_{ - 1.58}^{ + 2.31}$	${4.72}_{- 1.18}^{+ 1.79}$ $4.72_{ - 1.18}^{ + 1.79}$	${5.55}_{- 1.45}^{+ 1.78}$ $5.55_{ - 1.45}^{ + 1.78}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{5}$ $\Sigma _ \odot ^5$	4−5	1.8	${4.42}_{- 1.54}^{+ 1.96}$ $4.42_{ - 1.54}^{ + 1.96}$	${5.13}_{- 1.90}^{+ 1.98}$ $5.13_{ - 1.90}^{ + 1.98}$	${3.68}_{- 1.79}^{+ 1.63}$ $3.68_{ - 1.79}^{ + 1.63}$	${4.48}_{- 1.80}^{+ 1.76}$ $4.48_{ - 1.80}^{ + 1.76}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{6}$ $\Sigma _ \odot ^6$	5−6	2.3	${3.28}_{- 1.74}^{+ 1.66}$ $3.28_{ - 1.74}^{ + 1.66}$	${3.94}_{- 2.35}^{+ 1.81}$ $3.94_{ - 2.35}^{ + 1.81}$	${3.84}_{- 1.88}^{+ 1.79}$ $3.84_{ - 1.88}^{ + 1.79}$	${2.30}_{- 2.25}^{+ 1.20}$ $2.30_{ - 2.25}^{ + 1.20}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{7}$ $\Sigma _ \odot ^7$	6−7	2.3	${0.74}_{- 2.36}^{+ 0.26}$ $0.74_{ - 2.36}^{ + 0.26}$	${8.85}_{- 2.85}^{+ 3.07}$ $8.85_{ - 2.85}^{ + 3.07}$	${0.97}_{- 2.75}^{+ 0.38}$ $0.97_{ - 2.75}^{ + 0.38}$	${6.25}_{- 2.00}^{+ 2.87}$ $6.25_{ - 2.00}^{ + 2.87}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{8}$ $\Sigma _ \odot ^8$	7−8	3.4	${3.28}_{- 2.59}^{+ 1.76}$ $3.28_{ - 2.59}^{ + 1.76}$	${10.49}_{- 3.03}^{+ 3.41}$ $10.49_{ - 3.03}^{ + 3.41}$	${4.39}_{- 2.72}^{+ 2.06}$ $4.39_{ - 2.72}^{ + 2.06}$	${5.74}_{- 2.63}^{+ 2.40}$ $5.74_{ - 2.63}^{ + 2.40}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{9}$ $\Sigma _ \odot ^9$	8−9	3.4	${8.88}_{- 2.83}^{+ 3.18}$ $8.88_{ - 2.83}^{ + 3.18}$	${2.13}_{- 2.49}^{+ 1.13}$ $2.13_{ - 2.49}^{ + 1.13}$	${9.07}_{- 2.83}^{+ 3.29}$ $9.07_{ - 2.83}^{ + 3.29}$	${1.50}_{- 2.48}^{+ 0.72}$ $1.50_{ - 2.48}^{ + 0.72}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{10}$ $\Sigma _ \odot ^10$	9−10	3.4	${14.08}_{- 2.25}^{+ 5.56}$ $14.08_{ - 2.25}^{ + 5.56}$	${4.16}_{- 1.97}^{+ 1.81}$ $4.16_{ - 1.97}^{ + 1.81}$	${13.09}_{- 2.60}^{+ 5.19}$ $13.09_{ - 2.60}^{ + 5.19}$	${4.14}_{- 1.66}^{+ 2.03}$ $4.14_{ - 1.66}^{ + 2.03}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{9 T}$ $\Sigma _ \odot ^{9T}$	8−9	1.5/1.7	(1.5)	(1.5)	${1.48}_{- 1.19}^{+ 0.87}$ $1.48_{ - 1.19}^{ + 0.87}$	${14.56}_{- 0.67}^{+ 5.34}$ $14.56_{ - 0.67}^{ + 5.34}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{10 T}$ $\Sigma _ \odot ^{10T}$	9−10	1.9/1.7	(1.9)	(1.9)	${0.69}_{- 1.67}^{+ 0.25}$ $0.69_{ - 1.67}^{ + 0.25}$	${0.63}_{- 2.61}^{+ 0.15}$ $0.63_{ - 2.61}^{ + 0.15}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{11 T}$ $0.85_{ - 1.54}^{ + 0.44}$	10−11	1.9/1.7	(1.9)	(1.9)	${0.85}_{- 1.54}^{+ 0.44}$ $0.85_{ - 1.54}^{ + 0.44}$	${0.81}_{- 1.40}^{+ 0.40}$ $0.81_{ - 1.40}^{ + 0.40}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{12 T}$ $\Sigma _ \odot ^{12T}$	11−12	1.5/1.7	(1.5)	(1.5)	${1.48}_{- 1.48}^{+ 0.90}$ $1.48_{ - 1.48}^{ + 0.90}$	${2.68}_{- 1.02}^{+ 1.22}$ $2.68_{ - 1.02}^{ + 1.22}$	$M_{⊙} {pc}^{- 2} {Gyr}^{- 1}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$
$Σ_{⊙}^{T}$ $\Sigma _ \odot ^T$	All	31.4	${53.72}_{- 5.48}^{+ 6.89}$ $53.72_{ - 5.48}^{ + 6.89}$	${67.20}_{- 6.82}^{+ 5.99}$ $67.20_{ - 6.82}^{ + 5.99}$	${53.42}_{- 6.32}^{+ 7.11}$ $53.42_{ - 6.32}^{ + 7.11}$	${62.95}_{- 6.62}^{+ 6.24}$ $62.95_{ - 6.62}^{ + 6.24}$	$M_{⊙} {pc}^{- 2}$ ${M_ \odot }p{c^{ - 2}}Gy{r^{ - 1}}$

Notes. Columns are: parameter name, range of mass or age in solar masses or gigayears, respectively, value in the MS, posterior of the parameter in each of the executions (G13P-13, G13S-13, G13P-17, and G13S-17), and units of each parameter. The fitted parameters are: two IMF slopes, 11 SFH surface densities for the thin disc, and 4 SFH surface densities for the thick disc (for G13P-17 and G13S-17). For convenience, we also show the first slope of the IMF α₁ (fixed) and, in parenthesis, the value considered when the parameter was not fitted. In the last row, we show the total surface density resulting from the inference. In the MS column, we separate with a slash the thick disc SFH parameters 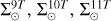$Σ_{⊙}^{9 T}, Σ_{⊙}^{10 T}, Σ_{⊙}^{11 T}$ $\Sigma _ \odot ^{9T},\Sigma _ \odot ^{10T},\Sigma _ \odot ^{11T}$ , and $Σ_{⊙}^{12 T}$ $\Sigma _ \odot ^{12T}$ considered for the executions G13P-13 and G13S-13, and those corresponding to the runs G13P-17 and G13S-17. The prior PDFs of all cases were Gaussians centred on the parameters in the MS column with variance σ_prior = 2 with the corresponding units. The PDFs of the SFHs were truncated at zero. The values for the inferred parameters were computed by fitting the SciPy Gaussian kernel-density estimator Virtanen et al. (2020) to the accepted combinations of parameters in the last 70 ABC steps (see Sect. 3.4). The posteriors shown in this table are presented considering the resulting most probable value of the distributions, as well as the 16^th and 84^th percentiles of each fitted parameter.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.