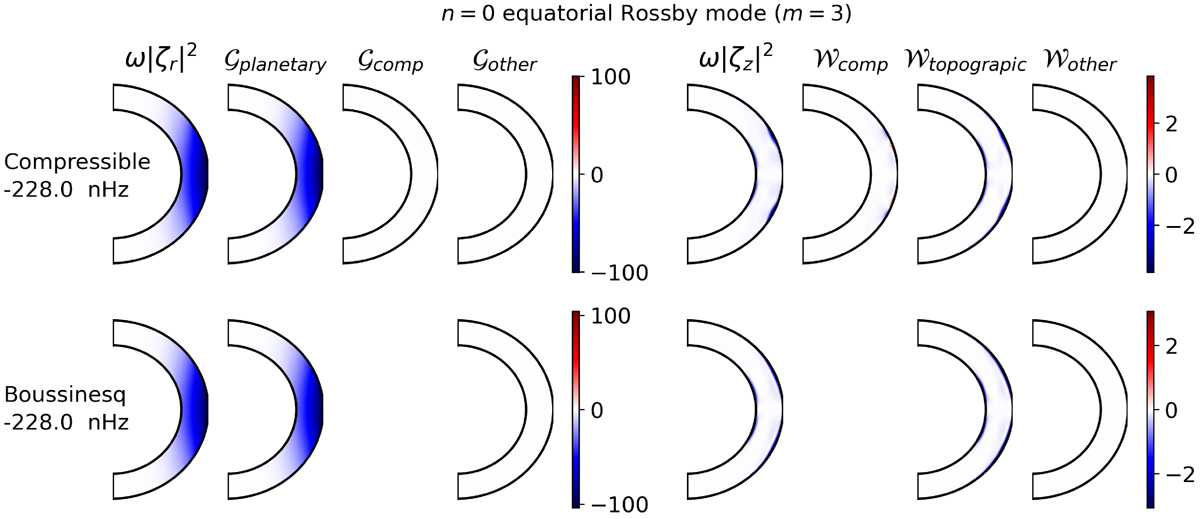
Fig. B.1.
Download original image
Relative importance of planetary β effect (![]() ), compressional β effect (
), compressional β effect (![]() ), topographical β effect (
), topographical β effect (![]() ) and other terms in the vorticity equation to determine the propagation and frequency of the n = 0 equatorial Rossby mode (m = 3) in the compressible and Boussinesq models, under uniform rotation. Refer to Eqs. (16) - (21) for the definition of the various quantities. A negative quantity implies that the associated physical effect promotes retrograde propagation, while a positive quantity implies that its physical effect promotes prograde propagation. The respective frequencies of the modes are specified on the left. We normalize the eigenfunctions from the different models to have the same integrated kinetic energy density such that the maximum absolute value of ℜ[ω|ζr|2] is 100 for the compressible model.
) and other terms in the vorticity equation to determine the propagation and frequency of the n = 0 equatorial Rossby mode (m = 3) in the compressible and Boussinesq models, under uniform rotation. Refer to Eqs. (16) - (21) for the definition of the various quantities. A negative quantity implies that the associated physical effect promotes retrograde propagation, while a positive quantity implies that its physical effect promotes prograde propagation. The respective frequencies of the modes are specified on the left. We normalize the eigenfunctions from the different models to have the same integrated kinetic energy density such that the maximum absolute value of ℜ[ω|ζr|2] is 100 for the compressible model.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


