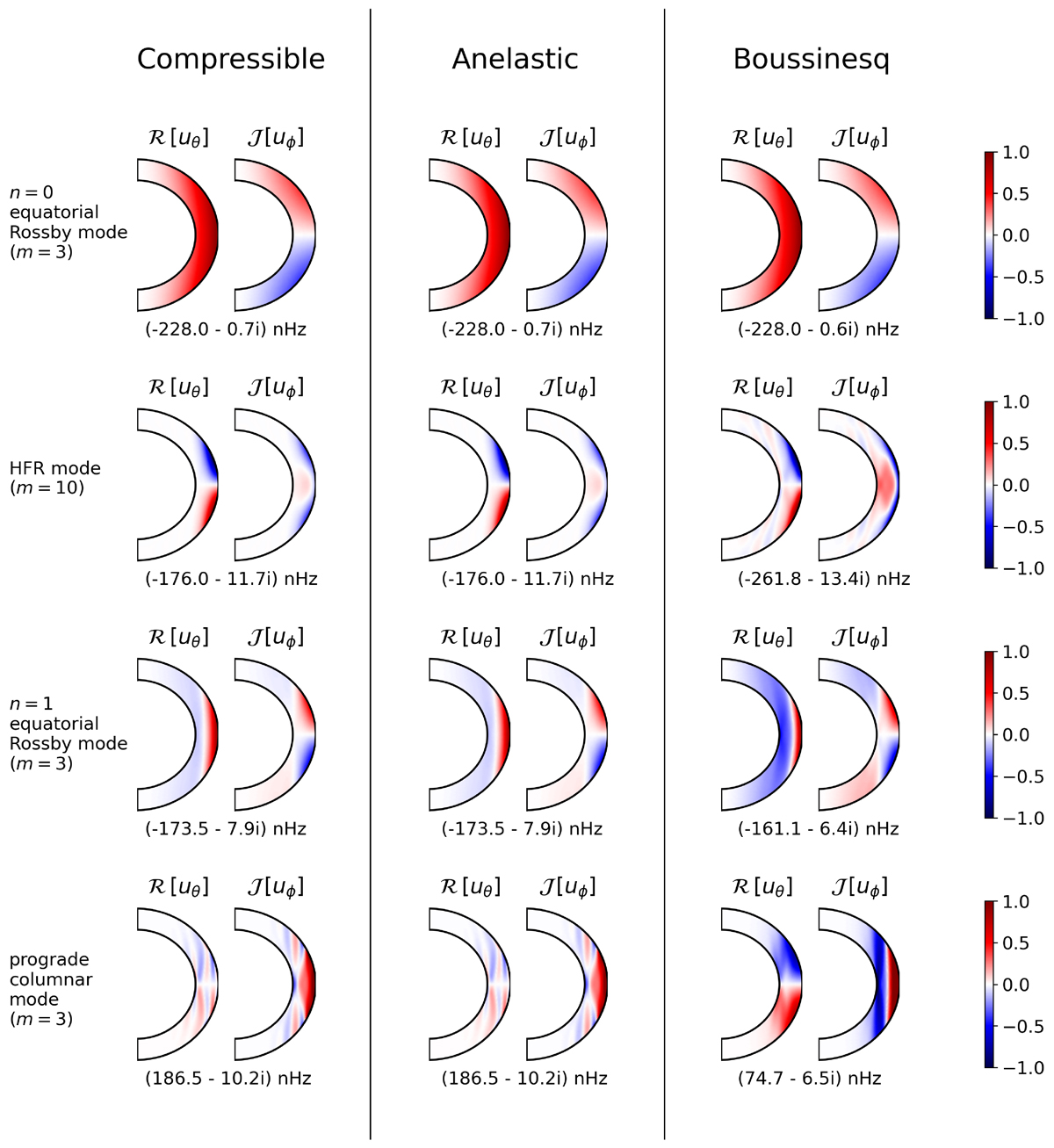
Fig. 2.
Download original image
Comparison of the eigenmodes of the different classes of inertial modes (see Table 1) computed using compressible, anelastic, and Boussinesq models under uniform rotation. Note that the unstable high-latitude inertial modes are absent under solid body rotation. Here, we plot the real part of uθ and the imaginary part of uϕ of the computed eigenmodes. The longitudes corresponding to the real and imaginary phases of the eigenfunctions are ϕ = ϕ0 and ϕ = ϕ0 − π/2m, respectively, where ϕ0 is a longitude, where uθ attains its maximum. The corresponding frequencies measured in the Carrington frame are stated below each eigenmode. The imaginary parts of the frequencies indicate the growth rates of the modes. All eigenfunctions are normalized such that the maximum of uθ is 1 m/s at the surface.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


