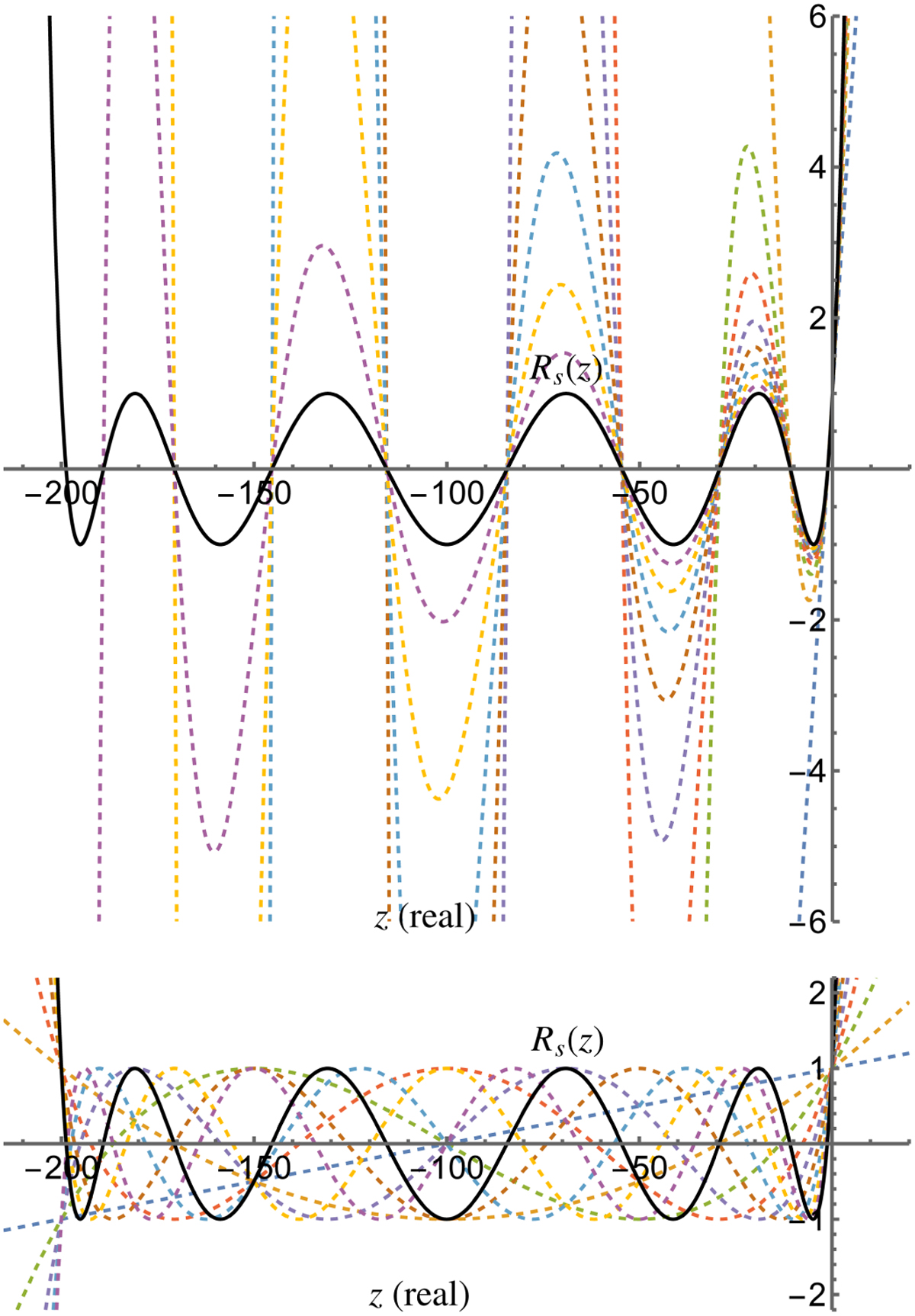
Comparison of the STS implementation in Eq. (12), top, and the stable implementation based on Chebyshev recurrence in Eq. (13), bottom, of the first-order Chebyshev method with an optimal stability polynomial given in Eq. (11). The stability polynomial R_s(z) defined in Eq. (11) for s = 10 (see black curves) and the stability polynomials of internal stages (related to k_j, j = 1 . . ., s − 1, see color curves) are plotted as a function of z which is assumed purely real here. The STS implementation exhibits poor internal stability, with internal stability polynomials oscillating with large amplitude resulting in instabilities with respect to roundoff errors, in contrast to the Chebyshev recurrence implementation defined in Eq. (13), with favorable internal stability where the amplitude of the internal stage stability polynomials remains bounded by 1.