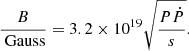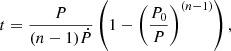| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202449657 | |
| Published online | 29 October 2024 | |
A binary supernova OB-runaway candidate inside Berkeley 97
Astrophysikalisches Institut und Universitäts-Sternwarte Jena, 07745 Jena, Germany
⋆ Corresponding author; baha.dincel@uni-jena.de
Received:
19
February 2024
Accepted:
27
August 2024
Aims. OB-runaway stars ejected by the binary supernova mechanism can be found near young open star clusters. In this paper, we present an OB-runaway candidate as a pre-SN binary companion to the progenitor of the pulsar PSR J2238+5903 inside the young open star cluster Berkeley 97.
Methods. We tried to find a kinematic outlier based on Gaia DR3 proper motions and parallaxes to be the pre-supernova binary companion to the progenitor of the pulsar. We took the spectra of two bright early B-type stars of the cluster, determined their effective temperature and surface gravity, and updated the parameters of the cluster. Through isochrone fitting of the color-magnitude diagram of the star cluster, we identified the members and determined the stellar parameters of the runaway star.
Results. Two bright members of the cluster, HD 240015 and HD 240016, are massive stars with spectral types of B0.5II and B1.5II and effective temperatures of Teff = 21 000 ± 1000 K and Teff = 24 000 ± 2000 K, respectively, as well as surface gravities of log(g[cm/s2]) = 3.0 ± 0.2. We find that Berkeley 97 is a star cluster with an age of log(age[yr]) = 7.1, an uncertainty of < 0.1 dex, and an interstellar extinction of AV = 3.1 ± 0.1 mag. The runaway star has an effective temperature of Teff = 12 250 ± 1750 K with a surface gravity of log(g[cm/s2]) = 4.38 ± 0.2 (B8V type star). By tracing back the proper motion of the runaway star, the explosion center was found for different possible pulsar ages of 10, 20, and 26.6 kyr. The pulsar moving out from the 20 kyr position must have a space velocity of ∼340 km s−1, which is consistent with the general pulsar velocity distribution. This supports the idea that the pulsar originated from the cluster as a result of a binary supernova. Despite its young age, τ < 26.6 kyr, the supernova remnant is not visible.
Key words: stars: early-type / stars: massive / stars: individual: Gaia DR3 2008384504995669248 / ISM: supernova remnants / pulsars: individual: PSR J2238+5903 / open clusters and associations: individual: Berkeley 97
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Around 30% of O-type stars and 5–10% of B-type stars are classified as runaways (Gies & Bolton 1986; Carretero-Castrillo et al. 2023). They show high space velocities greater than a specified velocity threshold of 25 km s−1 relative to the local average. The threshold value is the intersection point of the distribution curves of low-velocity and high-velocity stars (Tetzlaff et al. 2011; Tetzlaff 2013). The formation of runaway stars is explained by two independent mechanisms: the binary supernova (SN) scenario (BSS) and the dynamical ejection scenario (DES). The BSS describes how a stellar companion of an evolved star can obtain high space velocities due to the SN of the primary that disrupts the binary system. Here, sudden mass loss of the primary star during its SN results in an unbound orbit of the secondary star, usually catapulting the star outward with its orbital velocity during the SN if the mass loss is more than half of the total system’s mass before the SN (Blaauw 1961). Also, an asymmetry in the SN explosion gives a substantial kick to the neutron star (NS) (Wongwathanarat et al. 2013), which has been confirmed by the observed space velocity of the pulsars: 300–500 km s−1 (Lyne & Lorimer 1994; Allakhverdiev et al. 1997; Hobbs et al. 2005; Hansen & Phinney 1997). The high average kinetic energies of NSs imply that the binary systems are likely to be disrupted by the SN regardless of the amount of the ejected mass. The lack of pulsar companions to many of the OB-runaway stars (Sayer et al. 1996), the low rate of X-ray binaries, and the high rate of isolated NSs show that binary disruption is likely to occur in most cases (Guseinov et al. 2005).
In some cases, the compact object does not receive a significant kick and/or the majority of the total mass is stored on the secondary through conservative mass transfer; hence, the compact object remains bound to the companion star (van den Heuvel 1993). Runaway high-mass X-ray binaries such as 4U 1700−37 (Ankay et al. 2001), Vela X-1 (Kaper et al. 1997), and 4U 2206+54 (Hambaryan et al. 2022) are examples of this phenomenon.
The DES describes another creation channel for runaways inside a cluster, where many stars are ejected from their formation cluster due to gravitational instabilities during the early stages of cluster formation (Poveda et al. 1967). The most common scenario is a close encounter of a massive star (> 8 M⊙) and a bound binary or a close encounter of two bound binaries. In these cases, the close encounter will perturb the systems in such a way that both can become unbound. These then unbound stars can reach velocities similar to those of the BSS runaways since both mechanisms use orbital motions on similar scales, thus keeping a similar energy scale.
Kinematics of binary disruption due to an asymmetric SN explosion is widely discussed in Tauris & Takens (1998) while the observational efforts are concentrated on runaway–NS coupling and abundance investigations of runaway stars. Some examples of runaway-NS pairs (components are separated) are PSR 1706−16 – ζ Oph (Neuhäuser et al. 2020) and PSR J0826+2637 – HIP 13962 (Tetzlaff et al. 2014). Based on their motion in space, the pulsars and the corresponding runaway stars were traced back in time using 3D Monte Carlo simulations. They were found at the same position and at the same time inside a young open cluster (log[age(yr)] ≲7.7) hosting massive stars. The main uncertainties here lie in the unknown radial velocities (RVs) and the distance uncertainties of the NSs, so Monte Carlo simulations were done accounting for typical NS velocities and all other measurement uncertainties. The trace-back through the Galactic potential is sufficiently reliable for some ten million years. In the case of ζ Oph and PSR 1706, the time of the close approach (the SN) could be constrained to 1.78 ± 0.21 Myr and its distance to 107 ± 4 pc, and this position is consistent with an interstellar medium (ISM) cavity (Neuhäuser et al. 2020).
OB-type stars evolve fast, so they are guaranteed to be young (≲300 Myr) and fewer in number. This reduces the uncertainties when associating them with a cluster. Additionally, they are luminous (> 40 L⊙), making them a good target for astrometry and follow-up spectroscopy at larger distances. Also, massive progenitor stars tend to have massive or intermediate mass companions (Pinsonneault & Stanek 2006); hence, the runaway stars are expected to be mostly O- and B-type stars.
Through a systematic search for OB-runaway stars inside the SN remnants (SNRs), the OB-runaway star HD 37424 inside SNR S 147 was proven to have been ejected by the binary disruption due to the SN of the progenitor of S 147 and the pulsar PSR J0538+2817. A kinematic study has shown that the OB-runaway star and the pulsar were once at the same position in space, close to the geometric center of the SNR, at the same time, 30 ± 4 kyr (Dinçel et al. 2015). On the other hand, the OB-runaway search inside 12 other SNRs yielded an absence of strong OB-runaway candidates in these SNRs (Dinçel et al. 2024).
An alternative search area for BSS OB-runaways is open clusters. Independent of their flight trajectory coinciding with that of an NS, BSS runaways ejected from the cluster can be distinguished from DES runaways by their ejection time. The DES mechanism is mostly efficient at the early stages of an open cluster. Star clusters older than 3 Myr will have fully gone through their phase of frequent dynamical ejections (Oh & Kroupa 2016). Therefore, an ejection of an OB-type star at a point later than this age can be explained by BSS rather than DES. In Bhat et al. (2022), a BSS origin was suggested for several well-studied OB-runaways.
In this paper, we report the detection of an OB-runaway candidate ejected from the open star cluster Berkeley 97 within the last 26.6 kyr due to the SN of the progenitor star of PSR J0538+2817. The non-detection of an SNR from a core-collapse origin, after a relatively short time period, will be useful for understanding the SNR evolution.
2. Berkeley 97 and PSR J2238+5903
Based on the information from the updated parameters of 1743 Open Clusters catalog (Dias et al. 2021), Berkeley 97 is centered on the position α= 22h39m23.98s, δ = +59d00m16.6s, having an angular diameter of 5 arcmin. The distance and the extinction toward the cluster are d = 2485 ± 110 pc and AV = 2.539 ± 0.04 mag, respectively. The age is log(age[yr]) = 7.589 ± 0.381, with a metallicity of [Fe/H]= − 0.1 ± 0.026. The mean proper motion values of the cluster are μα* = −2.697 ± 0.176 mas yr−1 and μδ = −1.829 ± 0.144 mas yr−1. No RV measurement was previously mentioned for the cluster. The brightest members of Berkeley 97 are the two B-type stars HD 240015 and HD 240016 (Cannon 1928).
The radio-quiet γ-ray pulsar PSR J2238+5903 is located at α= 22h38m28.09s δ = +59d03m43.3s (Abdo et al. 2009), 7.9 arcmin (∼5.7 pc at a distance of 2485 pc) separated from Berkeley 97 (Fig. 1). The spin period and period derivatives of the pulsar are P = 162.7 ms and 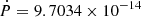 ss−1, respectively (Ray et al. 2011). The spin-down age is τ = 26.6 kyr. The pulsar has a typical dipole magnetic field strength of B = 4.02 × 1012 G, deduced from the
ss−1, respectively (Ray et al. 2011). The spin-down age is τ = 26.6 kyr. The pulsar has a typical dipole magnetic field strength of B = 4.02 × 1012 G, deduced from the 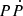 by the relation
by the relation
 |
Fig. 1. Space Telescope Science Institute 2nd Digitized Sky Survey’s red image of the open cluster Berkeley 97 (yellow circle) and PSR J2238+5903 (green cross) 7.9 arcmin separated from the center of the open cluster (yellow cross). |
The distance to the pulsar is suggested as d = 2.83 kpc in the Australia Telescope National Facility (ATNF) Pulsar Catalog1 based on measurements of absorption by neutral hydrogen combined with a model for differential rotation of the Galaxy. The neutral hydrogen column density determined from γ-ray observations is NH = 6.38 ± 0.04 × 1021 cm−2 (Abdo et al. 2013). Using the relation NH (cm−2) = (2.21 ± 0.09)×1021AV (mag) (Güver & Özel 2009), the extinction toward the pulsar is then AV = 2.89 ± 0.14 mag.
Pulsars constantly radiate their rotational energy and spin down. Their age can be estimated from the relation
where P0 is the initial spin period and n is the magnetic breaking index. Considering P ≫ P0 and adopting the breaking index, the theoretical value of n = 3, the characteristic age of the pulsar is calculated as 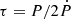 . This value is somewhat larger than the real age, as the pulsars have a small but non-zero P0. For example, the characteristic age of the Crab Pulsar is 1260 yr (Lyne et al. 2015), while the real age is 970 yr, found from the historical records (Stephenson & Green 2003). Another good example is PSR J0538+2817, having a characteristic age of ∼620 kyr and a real age of 30 ± 4 kyr, measured by calculating the flight time and confirmed by the pre-SN binary companion’s motion (Dinçel et al. 2015). They are both linked to SNRs. However, PSR J2238+5903 is not linked to any SNR despite its very young age. Also, the proper motion of the pulsar is unknown.
. This value is somewhat larger than the real age, as the pulsars have a small but non-zero P0. For example, the characteristic age of the Crab Pulsar is 1260 yr (Lyne et al. 2015), while the real age is 970 yr, found from the historical records (Stephenson & Green 2003). Another good example is PSR J0538+2817, having a characteristic age of ∼620 kyr and a real age of 30 ± 4 kyr, measured by calculating the flight time and confirmed by the pre-SN binary companion’s motion (Dinçel et al. 2015). They are both linked to SNRs. However, PSR J2238+5903 is not linked to any SNR despite its very young age. Also, the proper motion of the pulsar is unknown.
As the cluster catalog in Dias et al. (2021) is based on the Gaia DR2 catalog, we re-selected the members of the cluster and fit an isochrone on the color-magnitude diagram (CMD) based on Gaia DR3 data (Gaia Collaboration 2016, 2023). The parallax of HD 240016 and HD 240015 are ϖ = 0.3652 ± 0.0363 and 0.3583 ± 0.0125 mas, respectively. Thus, we selected the sources having parallax values between 0.3 and 0.4 mas detected on a significance larger than ten within 2.5 arcmin from the cluster center, and we found 25 such stars. The star Gaia DR3 2008383233685346560 lies significantly out of the isochrone in the CMD. Hence, we excluded this star from the membership. The average proper motion values of the 23 members are μα* = −2.753 ± 0.121 mas yr−1 and μδ = −1.915 ± 0.151 mas yr−1, where the errors are the standard deviations, which corresponds to only 1.5 and 1.9 km s−1, respectively, and shows that they exhibit a common proper motion (Table 1). One star, Gaia DR3 2008384504995669248, has a significantly different proper motion: μα* = −0.379 ± 0.025, μδ = −1.352 ± 0.024 mas yr−1.
Geometrical distances, proper motions, parallaxes, G-band brightnesses, and GBP–GRP color indices of the 23 members of Berkeley 97.
The geometrical distances of the potential members were retrieved from Bailer-Jones et al. (2021). The average of these distances is rgeo = 2733 pc, with a standard deviation of 163 pc, which is consistent with the average upper and lower errors of individual measurements, 160 and 170 pc, respectively.
The CMD – G versus (GBP–GRP) – of the potential members and the kinematical outlier was set and fit by theoretical isochrones.
We generated the isochrone tables involving stellar parameters as a function of the initial masses for a metallicity of [Fe/H]= − 0.1 with the CMD 3.72 website, using the “Parsec 1.2S” stellar evolutionary tracks (Chen et al. 2015) with bolometric corrections from Girardi et al. (2008), the extinction curve from Cardelli et al. (1989) and O’Donnell (1994), and with an extinction law RV = 3.1 (Fig. 2). We used the canonical two-part power-law initial mass function from Kroupa (2001, 2002).
 |
Fig. 2. CMD – G vs. (GBP–GRP) – Berkeley 97 potential members brighter than 17 mag in G-band. Left: CMD – G vs. (GBP–GRP) – of Berkeley 97. Unlike how it is mentioned in the literature, the isochrones fitting of the CMD are of log(age[yr]) = 6.8–7.1 for extinction values between and AV = 3.0–3.2 mag. For log(age[yr]) = 7.1, the isochrone represents hypothetical stars with masses of M = 1.8–16 M⊙. One star with a color index value larger than GBP–GRP > 2.0 mag is unlikely a member. Right: Close-up of the same CMD on the left. The brightest stars are HD 240016 and HD 240015 consecutively. The runaway candidate is shown as a red point. A typical 0.02 mag photometric error for each target is assigned to represent the uncertainty in the theoretical isochrones. The errors along the y-axis are smaller than the labels. |
To obtain a more precise and accurate cluster age, we observed the bright members of the cluster HD 240015 and HD 240016. These stars satisfy the kinematical and distance criteria and are not expected to be runaway stars.
3. Observations
We took the spectra of the bright members HD 240015 and HD 240016 in several observing epochs by using the Fibre Linked Échelle Astronomical Spectrograph (FLECHAS) (Mugrauer et al. 2014) on the 90-cm Schmidt telescope at the University Observatory Jena (Table 2). FLECHAS provides a resolving power of R ∼ 9200 and a wavelength range of 3900–8100 Å. We took the spectra with 2 × 2 pixel binning, which reduces the resolving power to R ∼ 7000. For optimal calibration, three arc (Th-Ar lamp) and flatfield images (Tungsten lamp), each with a detector integration time (DIT) of 1.5 s, were always taken immediately before the science exposures. The charge-coupled device of FLECHAS was always operated at a cooling temperature of −30°C. We took a set of three dark frames for each DIT used for the arc, flatfield, and science exposures and median combined them for efficient cosmic ray removal. Each spectrum and dark frame was divided into three frames in order to remove cosmic rays.
Dates of the observation of each star together with the signal-to-noise ratio obtained around the Hβλ4860 line.
We reduced the data obtained in the IRAF environment (Tody 1986). Dark frames were combined into master darks of all the used integration times and were then subtracted from the science, flat, and arc frames. We combined the three science frames with average sigma clipping rejection in order to remove cosmic rays. We extracted the flat and then the arc and the science frames by tracing each echelle aperture of the flat frame and then the science frame was divided by the flat frame. We identified the emission lines of the extracted arc spectrum and wavelength calibrated the science. After the wavelength calibration, the science was normalized. Finally, spectra in all the apertures were trimmed and combined to have one single spectrum.
We compared the spectra of HD 240015 and HD 240016 with the synthetic spectra, which were calculated from the Potsdam Wolf-Rayet/OB-star model atmospheres (Fig. 3)3. The spectra were calculated for a micro-turbulence velocity of vturb = 7 km s−1 and solar metallicity, with a grid resolution of 1000 K in temperature and 0.2 dex for the surface gravity, log (g).
 |
Fig. 3. Spectra of HD 240016 and HD 240015 with best-fitting model spectra overlayed. |
We applied boxcar smoothing to the synthetic spectra until the H intensity was equalized with that of the observed spectrum. After a visual comparison of the Hβ wings (4844–4874 Å), we chose the possible log (g) values as ![$ \log(\rm{g [cm/s^2]}) = 2.6 $](/articles/aa/full_html/2024/11/aa49657-24/aa49657-24-eq32.gif) –3.2. Then, we cross correlated the observed spectra with template spectra from 15 000–28 000 K temperatures, each separated into three log (g) values, 2.8, 3.0, and 3.2 with the fxcor (Fourier cross-correlation) task IRAF. We selected the spectra with the largest correlation height (Fig. 4) for a detailed visual inspection. We also measured the RVs of the stars in each observation epoch by Fourier cross-correlation in IRAF, with the best-fitting model spectra used as a template after the spectra were shifted in the wavelength space for the heliocentric RV.
–3.2. Then, we cross correlated the observed spectra with template spectra from 15 000–28 000 K temperatures, each separated into three log (g) values, 2.8, 3.0, and 3.2 with the fxcor (Fourier cross-correlation) task IRAF. We selected the spectra with the largest correlation height (Fig. 4) for a detailed visual inspection. We also measured the RVs of the stars in each observation epoch by Fourier cross-correlation in IRAF, with the best-fitting model spectra used as a template after the spectra were shifted in the wavelength space for the heliocentric RV.
 |
Fig. 4. Cross-correlation heights of the stars HD 240015 and HD 240016 with the template spectra for four different log (g) values between 2.6–3.2 dex. |
We measured the Doppler shift of the ISM lines on the stellar spectra, Na I-D1 and Na I-D2 by Gaussian fitting. The average heliocentric RV of interstellar Na I-D1 and Na I-D2 lines of HD 240015 and HD 240016 are RVNa = −25.1 ± 0.7 km s−1 and RVNa = −21.8 ± 0.6 km s−1, respectively. These values are considerably less than the measured heliocentric RV of the stars (Table 3). The RV variation in ISM lines might be due to the S/N and dispersion quality of the data.
Heliocentric RVs measured for stars and interstellar Na I-D1 and-D2 lines toward the stars.
The RVs measured for HD 240015 are consistent with each other within the errors. The weighted mean velocity is −47.5 km s−1, with an error of 4.8 km s−1, and the standard deviation is 4.2 km s−1. The weighted mean velocity of HD 240016 is the same, −47.5 ± 3.0 km s−1. However, the standard deviation of the measured velocities is high, 10.2 km s−1. They vary between −37 and −59 km s−1, implying the target is a spectroscopic binary. More observations are needed to constrain its orbital elements, but the binary parameters of this star are out of the scope of this work; hence, further observations were not needed. As there is no RV measurement for Berkeley 97 in the literature, −47.5 km s−1 can set a reference value for the RV of the OB-runaway candidate when it is determined with future observations.
The star HD 240016 shows no significant He IIλ 4686 but a relatively strong Si IIIλλ 4552-4568-4575. He IIλ 4686 appears at Teff = 22 000 K with ![$ \log(\rm{g [cm/s^2]}) = 3.0 $](/articles/aa/full_html/2024/11/aa49657-24/aa49657-24-eq33.gif) . So, the star should have a temperature smaller than Teff < 22 000 K. On the other hand, the star shows stronger O IIλ 4640 and λ 4650 (blend + C III) lines compared to the Teff = 18 000 K model with log(g[cm/s2]) = 2.8–3.0 as well as a weaker Mg IIλ 4481. Unlike HD 240016, HD 240015 shows a significant He IIλ 4686 line whose strength equals that of He Iλ 4713, implying a temperature of around Teff = 24 000 K. We note that the O IIλ 4640 and O IIλ 4349+4351 lines are weaker than the model spectrum, implying a higher or lower temperature. However, the major temperature indicator for this temperature range is the He IIλ 4686. The emission in the hydrogen lines and lower S/N increase the uncertainty in the stellar parameters of HD 240015. The temperature and log (g) values of the stars are given in Table 4.
. So, the star should have a temperature smaller than Teff < 22 000 K. On the other hand, the star shows stronger O IIλ 4640 and λ 4650 (blend + C III) lines compared to the Teff = 18 000 K model with log(g[cm/s2]) = 2.8–3.0 as well as a weaker Mg IIλ 4481. Unlike HD 240016, HD 240015 shows a significant He IIλ 4686 line whose strength equals that of He Iλ 4713, implying a temperature of around Teff = 24 000 K. We note that the O IIλ 4640 and O IIλ 4349+4351 lines are weaker than the model spectrum, implying a higher or lower temperature. However, the major temperature indicator for this temperature range is the He IIλ 4686. The emission in the hydrogen lines and lower S/N increase the uncertainty in the stellar parameters of HD 240015. The temperature and log (g) values of the stars are given in Table 4.
Measured parameters of the observed stars with the spectral types adopted in this work and the most precise spectral types available in the literature.
4. Results
The bright cluster members HD 240015 and HD 240016 are B0.5II and B1.5II type stars, confirming that the age of the cluster is ![$ \log(\rm{age[yr]}) = 7.1 $](/articles/aa/full_html/2024/11/aa49657-24/aa49657-24-eq34.gif) , with an uncertainty smaller than 0.1, and the extinction is AV = 3.1 ± 0.1 mag, for a metallicity of [Fe/H]= − 0.1 (Fig. 2). Based on the theoretical isochrones, both stars have a mass of
, with an uncertainty smaller than 0.1, and the extinction is AV = 3.1 ± 0.1 mag, for a metallicity of [Fe/H]= − 0.1 (Fig. 2). Based on the theoretical isochrones, both stars have a mass of 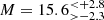 M⊙.
M⊙.
The star Gaia DR3 2008384504995669248, the kinematic outlier in the cluster, has a proper motion of μα* = −0.379 ±0.025 μδ = −1.352 ± 0.024 mas yr−1. The geometrical distance of the star is 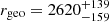 pc (Bailer-Jones et al. 2021), consistent with the cluster distance.
pc (Bailer-Jones et al. 2021), consistent with the cluster distance.
The proper motion of the star relative to the cluster average is μα* = 2.374 ± 0.146 μδ = 0.563 ± 0.175 mas yr−1, and the corresponding transverse velocity is 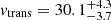 km s−1, which is above the runaway star velocity limit. Therefore, it is a strong runaway candidate. We derived the atmospheric parameters (Table 5) from the isochrone fit to the CMD of the cluster. The position of the star in the CMD does not exactly lie on the isochrone, which might be natural for relatively faint targets. It might also be exposed to a locally enhanced extinction due to a foreground cloudlet. The mass, and hence all the other corresponding parameters of the isochrone at the GBP–GRP value of the star, was taken as the lower limit, M = 2.2 M⊙, while the same at the G-band magnitude was taken as the upper limit of the mass, M = 3.5 M⊙. Hence, the star is predicted to be a main-sequence late B-type star.
km s−1, which is above the runaway star velocity limit. Therefore, it is a strong runaway candidate. We derived the atmospheric parameters (Table 5) from the isochrone fit to the CMD of the cluster. The position of the star in the CMD does not exactly lie on the isochrone, which might be natural for relatively faint targets. It might also be exposed to a locally enhanced extinction due to a foreground cloudlet. The mass, and hence all the other corresponding parameters of the isochrone at the GBP–GRP value of the star, was taken as the lower limit, M = 2.2 M⊙, while the same at the G-band magnitude was taken as the upper limit of the mass, M = 3.5 M⊙. Hence, the star is predicted to be a main-sequence late B-type star.
Derived and observed parameters of the OB-runaway candidate.
Gaia DR3 2008384504995669248 can be the pre-SN binary component to the progenitor of the pulsar. Hence, the flight trajectories of both objects must coincide at the same position. However, the pulsar proper motion is unknown. Yet, if a hypothetical trajectory of the pulsar yields a reasonable pulsar space velocity, then the link between the pulsar and the runaway is highly likely.
We found the explosion center by tracing back the peculiar proper motion of the runaway star (Fig. 5), which is the relative proper motion with regard to the cluster. The flight time is uncertain but limited to τ ∼ 26.6 kyr, as the characteristic age of the pulsar generally sets an upper limit for its real age. The pulsar velocity is calculated by the distance taken by the pulsar, from the explosion center, divided by the exercised flight time. The runaway tracing back for 20 kyr (considered pulsar age/flight time) gives a pulsar velocity of vsp∼340 km s−1, which is a typical value for the space velocity of a pulsar (Lyne & Lorimer 1994). Flight times as low as 10 kyr yield a velocity of vsp ∼ 650 km s−1, which is more unlikely. The lowest possible velocity is 246 km s−1, calculated for 26.6 kyr. Therefore, the kinematic age of the pulsar should be about 20 kyr. Thus, the SN should have occurred about 20 kyr ago. Furthermore, for such high kick velocities, binary disruption is likely.
 |
Fig. 5. Possible explosion center and pulsar’s flight trajectory. Left: Tracing back of the runaway candidate (green lines) for 20 kyr. The explosion center is within the cluster. Right: Hypothetical flight trajectory (Euclidian) of the pulsar for the same time span. The pulsar velocity, in this case, is ∼340 km s−1. |
Although a proper motion measurement is not possible for the pulsar with the existing data, we sketched all of the positions available in the literature with the epoch of observations on the X-ray image (Fig. 6). The γ-ray detections have substantial positional uncertainties of several arcminutes. There are four relatively precise detections: two from γ-ray timing studies, one from an X-ray point source, and one from an IR source in the K-band (Table 6). The theoretical proper motion of the pulsar for an age of 20 kyr is only ∼27 mas yr−1 with a parallactic angle of ∼298°, while the positional uncertainties are still large: ∼1 arcsec. Also, the positional uncertainties determined by the first γ-ray timing (MJD = 54 800) are probably underestimated because the position is largely (several arcseconds) separated from the other positions. Also, γ-ray positions are always less precise compared to X-ray positions. On the other hand, the parallactic angle between the IR and the X-ray sources (MJDs; 54 322 and 56 038.411) is ∼305°, consistent with our expectation. Future X-ray and IR observations might be helpful to at least see the direction of motion. Also, an independent study should verify that these two sources are the X-ray and IR counterparts of the pulsar.
 |
Fig. 6. Centre de Données astronomiques de Strasbourg (CDS) Hierarchical Progressive Survey (HiPS) color composite image of the region around the pulsar, retrieved from Aladin Sky Atlas. Red represents the soft X-ray (0.5–1.2 keV) data taken by Chandra ACIS, while green is the medium band (1.2–2.0 keV) of the same. The source seen in the image is most probably the X-ray counterpart of PSR J2238+5903. The point sources mentioned in Table 6 are shown with a white X with the corresponding MJDs and positional error ellipses. The green vector shows the direction of motion if the pulsar originated from the position we found using the OB-runaway proper motion. |
Possible positions of the pulsar in the literature.
We also searched for an optical counterpart using the Gaia DR3 catalog within 20 arcseconds from the pulsar. Yet we did not find any optical source with a significantly high proper motion, namely, > 8 mas yr−1 (∼100 km s−1).
Based on the isochrones (Fig. 2) and using the initial mass function from Kroupa (2001, 2002), the mass of the OB-runaway candidate is M ∼ 3 M⊙, while the maximum mass among the members of the cluster is M ∼ 16 M⊙. Hence, the progenitor zero-age main-sequence mass should be close to this value: Mprogenitor ∼ 16 M⊙. Assuming a circular orbit, we reconstructed the hypothetical pre-SN binary system for two different orbital velocities assumed for the secondary (Table 7). The first velocity is the 2D peculiar transverse velocity of the runaway star (the pre-SN secondary), 30 km s−1, while the other one is a hypothetical 3D peculiar velocity of the runaway, 42 km s−1, calculated by assuming the star has the same peculiar velocity in the radial direction as the transverse velocity. We note that the 2D peculiar transverse velocity of the runaway star is the lower limit of the 3D peculiar velocity. Also, the RV can surely be even larger than the assumed value. Considering the possible mass loss during the post-main sequence evolution (van den Heuvel 1976; Taam & Sandquist 2000; Zapartas et al. 2017), we calculated the parameters for three different pre-SN progenitor masses 5, 10, and 16 M⊙.
Calculated parameters of the pre-SN binary for two different peculiar velocities of 30 (top) and 42 (bottom) km s−1.
The Roche lobe radius 762 R⊙ for 42 km s−1 implies that the system might have been an interacting binary at the supergiant phase of the primary (van den Heuvel 1993; Woosley et al. 1995), as the massive stars can expand beyond this size, as in the star VY CMa, 1420 R⊙ (Wittkowski et al. 2012). Thus, they can fill their Roche lobe and accrete matter onto their companion. However, for 30 km s−1, the minimum velocity of the runaway, the system is likely to be detached (Table 7).
5. Discussion
A characteristic age of τ = 26.6 kyr implies that an SNR related to the pulsar should still be visible. An SNR at this age should either show a radio shell through non-thermal synchrotron radiation of accelerated electrons, possibly with a hot X-ray shell, or optical emission of recombining H atoms and forbidden transitions from various atoms. However, no SNR is mentioned in the literature that can be related to the pulsar. We checked archival images taken in the radio, optical, and X-ray spectral range toward the pulsar and the cluster to find a shell or pulsar wind nebula (PWN) structure. However, no sign of an SNR shell or a PWN was found in the Canadian Galactic Plane Survey (CGPS) 1420 MHz (Fig. 7), the Space Telescope Science Institute 2nd Digitized Sky Survey’s red images, or the ROSAT X-ray images.
 |
Fig. 7. CGPS 1420 MHz image of the region. No shell structure of an SNR is detectable, while the shells of the bright SNR G109.1−1.0 and a faint SNR G108.2−0.6 can be clearly detected. A green circle shows Berkeley 97. The bar is 33 arcmin (26 pc) long. |
Considering the typical SNR dissipation time of 100 kyr, one expects to find 2000 SNRs with a galactic SN rate of two SN per century within the Milky Way (Tammann et al. 1994). However, observations have shown evidence of only 300 SNRs, which is inconsistent with the expected number of SNe (Green 2009). One reason might be that some SNe do not produce a visible SNR due to the low density of the ambient medium. The SNR is not able to sweep up enough interstellar material and thus cannot enter a Sedov or radiative phase for a long time. Such bubbles can form around the young open clusters and OB associations through strong winds or the SNe of massive stars. Another possibility is that the SNR interacts with dense molecular clouds, and the shock wave loses its entire energy and merges with the ISM much sooner than expected. A good example is SNR CTB 109, whose shock wave dissipated on the western side where it had an interaction with a giant molecular cloud (Sasaki et al. 2006). The lower the explosion energy, the lower the cloud density required for such dispersion.
We checked the 21 cm-H I images from CGPS extending from 0 to −80 km s−1 local standard of rest (LSR) velocities to find a bubble inside H I clouds resulting from the ionization of hydrogen due to the hot SNR or the strong winds and UV radiation from the massive stars of Berkeley 97. The cluster is surrounded by a void at vLSR = −29 ± 2 km s−1 (Fig. 8). The void has an angular diameter of ∼33 arcmin, which translates to a physical diameter of 26 pc at a distance of 2.7 kpc. The diameter is consistent with the diameter of an evolved SNR.
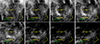 |
Fig. 8. CGPS 21-cm H I images of Berkeley 97 and surroundings. There was no sign of an SNR in any wavebands; however, a void is present at vLSR = −29 ± 2 km s−1. The local standard of rest velocities (vLSR) are given in each image. The green circle shows Berkeley 97. The bar is 33 arcmin (26 pc) long. |
The tracing back of the pulsar to the runaway star implies a kinematical age of 20 kyr. Considering the case of an extended free expansion phase, the SNR blast wave moves freely at a constant high velocity, such as 5000 km s−1 (shock velocity from a core-collapse of a massive star). In 20 kyr, it expands up to a radius of about 100 pc, which is incomparably larger than the void radius of ∼13 pc. The SNR must expand very slowly (∼1250 km s−1) in this void for only 10 kyr, which dictates a high pulsar space velocity of ∼650 km s−1. The SNR is likely to have already interacted with the ambient medium. Therefore, the possible explanation is that the SNR has already merged with the ISM and faded away. This might be explained by a low SN explosion energy, as in the case of the Crab Nebula (∼1050 erg) (Yang & Chevalier 2015). The SNR evolved slowly in a relatively hot medium with a high speed of sound so that the expansion velocity became subsonic at an early age. In either case, the explosion energy should be very low. A third option can be that the cluster is not related to the H I clouds, and the ejecta expands freely for longer distances.
The massive members of Berkeley 97, HD 240015 and HD 240016, are definitely not runaway stars, yet they show bow-shock features in the IR (Chick et al. 2020). However, considering the age of the cluster, 107.1 (12.59 Myr), the star formation must be mostly completed, and the dust around the cluster should have been dispersed by the strong UV radiation, winds and SNe of the massive members.
Dust is mainly formed by AGB stars, SNRs, and PWNe. Therefore, the dissipated SNR or the wind nebula that the pulsar once had might be an agent that produces the dust heated by the bow shocks today. The bow shock direction does not point toward the explosion center (Fig. 9). Hence, it is not expanding from the center. Although the dynamics are not clearly understood, one can speculate that some part of the dust is dragged inward by the reverse shock and interacts with the massive stars’ magnetosphere. A spectrum of the IR emission can reveal if the dust has SN content (e.g., enrichment in α-process elements).
 |
Fig. 9. WISE W4 image of the cluster. The bow shock features are clearly seen around the massive stars of the cluster. The explosion center is the larger green circle. |
On the other hand, the generation of the bow shock by two non-runaway stars can be explained by the fact that the whole cluster has a peculiar space velocity. In the direction of l = 110°, at around 2.7 kpc, local bodies can have a wide range of velocities between −35 and −55 km s−1 due to the Perseus arm density shock wave (Foster & MacWilliams 2006). Such an explanation can be valid in this case, the cluster penetrates to a low-velocity region and shows a relative RV of ∼−22 km s−1, which is the difference between the RV of HD 240015 and the average ISM lines.
6. Summary
Through careful member selection using Gaia DR3 data and spectroscopic confirmation of its bright members, we find that Berkeley 97 is a young open cluster at an age of log(age[yr]) = 7.1 with an uncertainty of < 0.1 dex. The extinction toward the cluster is AV = 3.1 ± 0.1 mag.
The origin of the γ-ray pulsar PSR J2238+5903 is likely to be the cluster. The hypothetical space velocities calculated for the pulsar in case of ejection from the cluster are consistent with the typical space velocities of pulsars in general.
The star Gaia DR3 2008384504995669248 can be the pre-SN companion to the progenitor of the pulsar. It is a late B-type runaway star (B8V) with a 2D peculiar transverse velocity of ∼30 km s−1.
The SNR should have been detectable for a maximum age of 26.6 kyr. However, it does not manifest itself at any wavelength. The explosion energy of the SNR must have been very low, and the shock wave either has already dissipated and merged into the ISM or is very slowly expanding into the low-density ambient medium.
The massive members HD 240015 and HD 240016 show bow-shock features in mid-IR, although they are not runaway stars. The relic dust from the star formation should have already been dispersed by the cluster; therefore, it might have been produced by SN or the PWN recently. However, it is also possible that the cluster penetrates a lower velocity region on the edge of the Parseus arm density wave.
Acknowledgments
This work is based on observations obtained with telescopes of the University Observatory Jena, operated by the Astrophysical Institute of the Friedrich-Schiller-University Jena. We would like to thank the referee of this paper for carefully reading our manuscript and for their constructive comments which contributed to improving the quality of the paper. We appreciate the observational support from A. Mella Aceituno. This research has made use of the “Aladin sky atlas” developed at CDS, Strasbourg Observatory, France. We gratefully acknowledge the support of NASA and the contributors of the SkyView surveys. The Digitized Sky Survey was produced at the Space Telescope Science Institute under U.S. Government grant NAG W-2166. The images of these surveys are based on photographic data obtained using the Oschin-Schmidt Telescope on Palomar Mountain and the UK Schmidt Telescope. The plates were processed into the present compressed digital form with the permission of these institutions. The research presented in this paper has used data from the Canadian Galactic Plane Survey, a Canadian project with international partners supported by the Natural Sciences and Engineering Research Council. We acknowledge the ROSAT data archive provided by the Max-Planck-Institute for Extraterrestrial Physics, Garching, Germany.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 325, 840 [Google Scholar]
- Abdo, A. A., Ajello, M., Allafort, A., et al. 2013, ApJS, 208, 17 [Google Scholar]
- Allakhverdiev, A. O., Guseinov, O. H., Tagieva, S. O., & Yusifov, I. M. 1997, Astron. Rep., 41, 257 [NASA ADS] [Google Scholar]
- Ankay, A., Kaper, L., de Bruijne, J. H. J., et al. 2001, A&A, 370, 170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bhat, A., Irrgang, A., & Heber, U. 2022, A&A, 663, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaauw, A. 1961, BAIN, 15, 265 [Google Scholar]
- Cannon, A. J. 1928, Ann. Harv. College Obs., 100, 49 [NASA ADS] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carretero-Castrillo, M., Ribó, M., & Paredes, J. M. 2023, A&A, 679, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]
- Chick, W. T., Kobulnicky, H. A., Schurhammer, D. P., et al. 2020, ApJS, 251, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Monteiro, H., Moitinho, A., et al. 2021, MNRAS, 504, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Dinçel, B., Neuhäuser, R., Yerli, S. K., et al. 2015, MNRAS, 448, 3196 [CrossRef] [Google Scholar]
- Dinçel, B., Uzuner, M., Neuhäuser, R., et al. 2024, MNRAS, 531, 4212 [CrossRef] [Google Scholar]
- Foster, T., & MacWilliams, J. 2006, ApJ, 644, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R., & Bolton, C. T. 1986, ApJS, 61, 419 [Google Scholar]
- Girardi, L., Dalcanton, J., Williams, B., et al. 2008, PASP, 120, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2009, VizieR Online Data Catalog: VII/253 [Google Scholar]
- Guseinov, O. H., Ankay, A., & Tagieva, S. O. 2005, Astrophysics, 48, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [Google Scholar]
- Hambaryan, V., Stoyanov, K. A., Mugrauer, M., et al. 2022, MNRAS, 511, 4123 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., & Phinney, E. S. 1997, MNRAS, 291, 569 [NASA ADS] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [Google Scholar]
- Hohle, M. M., Neuhäuser, R., & Schutz, B. F. 2010, Astron. Nachr., 331, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Kaper, L., van Loon, J. T., Augusteijn, T., et al. 1997, ApJ, 475, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, M., Ray, P. S., Johnston, S., Shannon, R. M., & Camilo, F. 2015, ApJ, 814, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Lucas, P. W., Hoare, M. G., Longmore, A., et al. 2008, MNRAS, 391, 136 [Google Scholar]
- Lyne, A. G., & Lorimer, D. R. 1994, Nature, 369, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Jordan, C. A., Graham-Smith, F., et al. 2015, MNRAS, 446, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Mugrauer, M., Avila, G., & Guirao, C. 2014, Astron. Nachr., 335, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., Gießler, F., & Hambaryan, V. V. 2020, MNRAS, 498, 899 [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Oh, S., & Kroupa, P. 2016, A&A, 590, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., & Stanek, K. Z. 2006, ApJ, 639, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Poveda, A., Ruiz, J., & Allen, C. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 86 [Google Scholar]
- Ray, P. S., Kerr, M., Parent, D., et al. 2011, ApJS, 194, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, M., Kothes, R., Plucinsky, P. P., Gaetz, T. J., & Brunt, C. M. 2006, ApJ, 642, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Sayer, R. W., Nice, D. J., & Kaspi, V. M. 1996, ApJ, 461, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Stephenson, F. R., & Green, D. A. 2003, J. Astron. Hist. Heritage, 6, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., & Sandquist, E. L. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Loeffler, W., & Schroeder, A. 1994, ApJS, 92, 487 [Google Scholar]
- Tauris, T. M., & Takens, R. J. 1998, A&A, 330, 1047 [NASA ADS] [Google Scholar]
- Tetzlaff, N. U. 2013, Ph.D. Thesis, Friedrich Schiller University of Jena, Germany [Google Scholar]
- Tetzlaff, N., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 410, 190 [Google Scholar]
- Tetzlaff, N., Dinçel, B., Neuhäuser, R., & Kovtyukh, V. V. 2014, MNRAS, 438, 3587 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, SPIE Conf. Ser., 627, 733 [Google Scholar]
- van den Heuvel, E. P. J. 1976, IAU Symp., 73, 35 [Google Scholar]
- van den Heuvel, E. P. J. 1993, Space Sci. Rev., 66, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Liu, J., Qiu, Y., et al. 2016, ApJS, 224, 40 [Google Scholar]
- Wittkowski, M., Hauschildt, P. H., Arroyo-Torres, B., & Marcaide, J. M. 2012, A&A, 540, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wongwathanarat, A., Janka, H.-T., & Müller, E. 2013, A&A, 552, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., Langer, N., & Weaver, T. A. 1995, ApJ, 448, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., & Chevalier, R. A. 2015, ApJ, 806, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Zapartas, E., de Mink, S. E., Van Dyk, S. D., et al. 2017, ApJ, 842, 125 [CrossRef] [Google Scholar]
All Tables
Geometrical distances, proper motions, parallaxes, G-band brightnesses, and GBP–GRP color indices of the 23 members of Berkeley 97.
Dates of the observation of each star together with the signal-to-noise ratio obtained around the Hβλ4860 line.
Heliocentric RVs measured for stars and interstellar Na I-D1 and-D2 lines toward the stars.
Measured parameters of the observed stars with the spectral types adopted in this work and the most precise spectral types available in the literature.
Calculated parameters of the pre-SN binary for two different peculiar velocities of 30 (top) and 42 (bottom) km s−1.
All Figures
 |
Fig. 1. Space Telescope Science Institute 2nd Digitized Sky Survey’s red image of the open cluster Berkeley 97 (yellow circle) and PSR J2238+5903 (green cross) 7.9 arcmin separated from the center of the open cluster (yellow cross). |
| In the text | |
 |
Fig. 2. CMD – G vs. (GBP–GRP) – Berkeley 97 potential members brighter than 17 mag in G-band. Left: CMD – G vs. (GBP–GRP) – of Berkeley 97. Unlike how it is mentioned in the literature, the isochrones fitting of the CMD are of log(age[yr]) = 6.8–7.1 for extinction values between and AV = 3.0–3.2 mag. For log(age[yr]) = 7.1, the isochrone represents hypothetical stars with masses of M = 1.8–16 M⊙. One star with a color index value larger than GBP–GRP > 2.0 mag is unlikely a member. Right: Close-up of the same CMD on the left. The brightest stars are HD 240016 and HD 240015 consecutively. The runaway candidate is shown as a red point. A typical 0.02 mag photometric error for each target is assigned to represent the uncertainty in the theoretical isochrones. The errors along the y-axis are smaller than the labels. |
| In the text | |
 |
Fig. 3. Spectra of HD 240016 and HD 240015 with best-fitting model spectra overlayed. |
| In the text | |
 |
Fig. 4. Cross-correlation heights of the stars HD 240015 and HD 240016 with the template spectra for four different log (g) values between 2.6–3.2 dex. |
| In the text | |
 |
Fig. 5. Possible explosion center and pulsar’s flight trajectory. Left: Tracing back of the runaway candidate (green lines) for 20 kyr. The explosion center is within the cluster. Right: Hypothetical flight trajectory (Euclidian) of the pulsar for the same time span. The pulsar velocity, in this case, is ∼340 km s−1. |
| In the text | |
 |
Fig. 6. Centre de Données astronomiques de Strasbourg (CDS) Hierarchical Progressive Survey (HiPS) color composite image of the region around the pulsar, retrieved from Aladin Sky Atlas. Red represents the soft X-ray (0.5–1.2 keV) data taken by Chandra ACIS, while green is the medium band (1.2–2.0 keV) of the same. The source seen in the image is most probably the X-ray counterpart of PSR J2238+5903. The point sources mentioned in Table 6 are shown with a white X with the corresponding MJDs and positional error ellipses. The green vector shows the direction of motion if the pulsar originated from the position we found using the OB-runaway proper motion. |
| In the text | |
 |
Fig. 7. CGPS 1420 MHz image of the region. No shell structure of an SNR is detectable, while the shells of the bright SNR G109.1−1.0 and a faint SNR G108.2−0.6 can be clearly detected. A green circle shows Berkeley 97. The bar is 33 arcmin (26 pc) long. |
| In the text | |
 |
Fig. 8. CGPS 21-cm H I images of Berkeley 97 and surroundings. There was no sign of an SNR in any wavebands; however, a void is present at vLSR = −29 ± 2 km s−1. The local standard of rest velocities (vLSR) are given in each image. The green circle shows Berkeley 97. The bar is 33 arcmin (26 pc) long. |
| In the text | |
 |
Fig. 9. WISE W4 image of the cluster. The bow shock features are clearly seen around the massive stars of the cluster. The explosion center is the larger green circle. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.