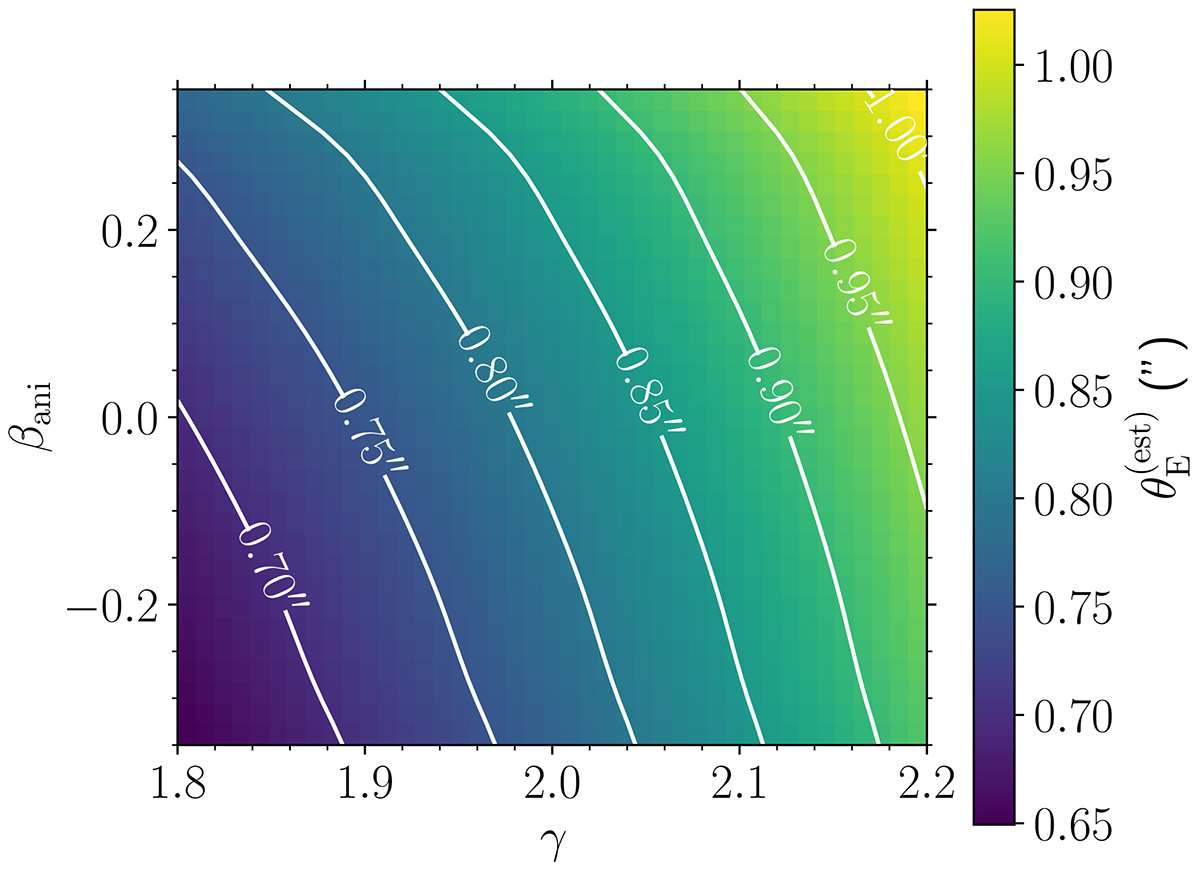
Estimated Einstein radius of a power-law lens with θ_E = 1″, as a function of density slope and orbital anisotropy. The lens is at z_g = 0.2, with a half-light radius R_e = 7 kpc, and the Einstein radius is computed with respect to a source at z_s = 0.6. White lines connect points of constant ${\theta }_{\mathrm{E}}^{(\mathrm{est})}$. These are also points of constant velocity dispersion. In general, ${\theta }_{\mathrm{E}}^{(\mathrm{est})}<{\theta }_{\mathrm{E}}$: this is because the line-of-sight velocity dispersion, which is used to estimate ${\theta }_{\mathrm{E}}^{(\mathrm{est})}$, is smaller than the three-dimensional velocity dispersion of a singular isothermal sphere, due to projection effects.