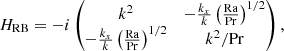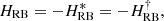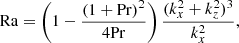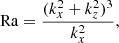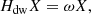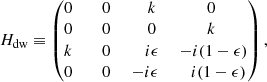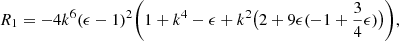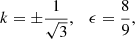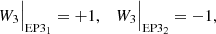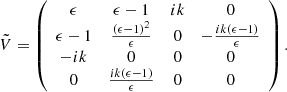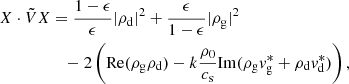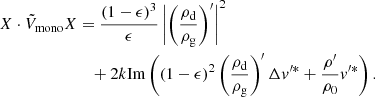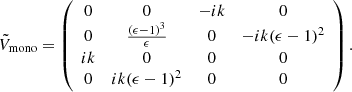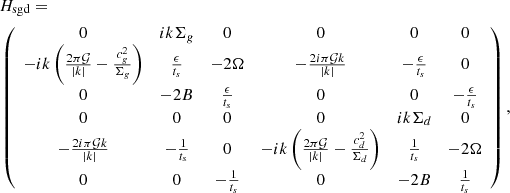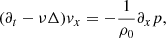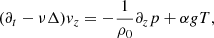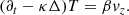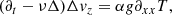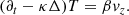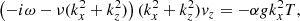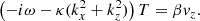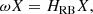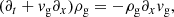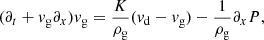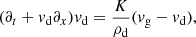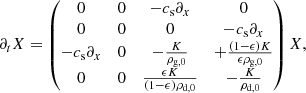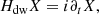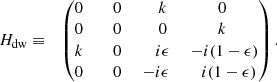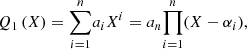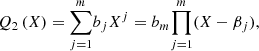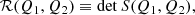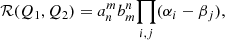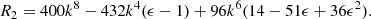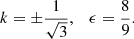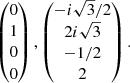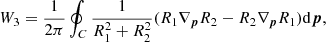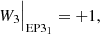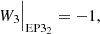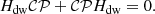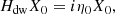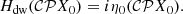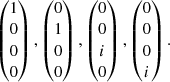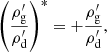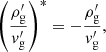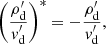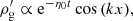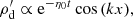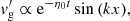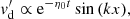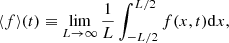| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A237 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348710 | |
| Published online | 18 September 2024 | |
𝒫𝒯 and anti-𝒫𝒯 symmetries for astrophysical waves
Univ Lyon, Univ Lyon1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval, France
Received:
22
November
2023
Accepted:
28
May
2024
Context. Discrete symmetries have found numerous applications in photonics and quantum mechanics, but remain little studied in fluid mechanics, particularly in astrophysics.
Aims. We aim to show how 𝒫𝒯 and anti-𝒫𝒯 symmetries determine the behaviour of linear perturbations in a wide class of astrophysical problems. They set the location of ‘exceptional points’ in the parameter space and the associated transitions to instability, and are associated with the conservation of quadratic quantities that can be determined explicitly.
Methods. We study several classical local problems: the gravitational instability of isothermal spheres and thin discs, the Schwarzschild instability, the Rayleigh-Bénard instability and acoustic waves in dust–gas mixtures. We calculate the locations and the order of the exceptional points using the resultant of two univariate polynomials, as well as the conserved quantities in the different regions of the parameter space using Krein theory.
Results. All problems studied here exhibit discrete symmetries, even though Hermiticity is broken by different physical processes (self-gravity, buoyancy, diffusion, and drag). This analysis provides genuine explanations for certain instabilities, and for the existence of regions in the parameter space where waves do not propagate. Those two aspects correspond to regions where 𝒫𝒯 and anti-𝒫𝒯 symmetries are broken respectively. Not all instabilities are associated to symmetry breaking (e.g. the Rayleigh-Benard instability).
Key words: diffusion / hydrodynamics / instabilities / waves
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Many astrophysical systems, such as stars and discs, are often treated as fluids (e.g. Pringle & King 2007; Armitage 2010). The properties and the stability of the corresponding linear modes are usually analysed with methods that, to our knowledge, do not fully exploit the symmetries of the perturbed system with respect to parity 𝒫 and time 𝒯.
Some of the most striking properties of 𝒫𝒯-symmetric systems emerged in the quantum physics community with the seminal paper by Bender & Boettcher (1998), the first non-Hermitian quantum Hamiltonian situation with a real spectrum, which paved the way to open quantum systems. This framework has been extended to situations exhibiting a spontaneous 𝒫𝒯-symmetry-breaking phase transition (Bender et al. 1999, 2002). Generalisations to quantum field theory were developed by Bender et al. (2004) and considerations of the observables of such systems were put forward by Mostafazadeh & Batal (2004). 𝒫𝒯 symmetry has been a particularly powerful tool in optics and photonics, where it has led to the development of novel designs with special properties. The analogy with quantum mechanics comes from the fact that beam dynamics is governed by a Schrödinger equation, where the optical index behaves as a complex potential, which can be designed to satisfy 𝒫𝒯 symmetry (El-Ganainy et al. 2007; Makris et al. 2008). Klaiman et al. (2008) identified a spontaneous breaking of 𝒫𝒯 symmetry in a waveguide. Musslimani et al. (2008) investigated the non-linear propagation of optical solitons in 𝒫𝒯-symmetric refraction indexes. (Guo et al. 2009) and (Rüter et al. 2010) made the first observations of 𝒫𝒯 symmetry in optics with a complex index. A decade of developments of 𝒫𝒯 symmetry in photonics lead to a multitude of applications (e.g. Feng et al. 2017; El-Ganainy et al. 2018; Özdemir et al. 2019). Feng et al. (2014) used spontaneous breaking of 𝒫𝒯 symmetry to design a pure single-mode laser. Peng et al. (2014) propose a design for a low-power optical diode, where the non-linear regime of the 𝒫𝒯 symmetry induces non-reciprocal propagation. Lin et al. (2011), Regensburger et al. (2012) and Feng et al. (2013) used 𝒫𝒯 symmetry in periodic systems (through gratings, periodic crystals, and lattices) to design unidirectional invisibility. 𝒫𝒯-symmetric degeneracies are now used for their high resonant sensitivity in optical cavities (Hodaei et al. 2017). Anti-𝒫𝒯 symmetry has also found application in novel optical designs (e.g. Ge & Türeci 2013; Zhang et al. 2020a,b). The topological properties of 𝒫𝒯-symmetric systems have recently been investigated in the context of fluid dynamics (Fu & Qin 2024). 𝒫𝒯 and anti-𝒫𝒯 symmetries have only recently been taken into account in fluid systems to directly constrain fluid flows and instabilities by spontaneous symmetry breaking (Qin et al. 2019; Fu & Qin 2020; David et al. 2022). The 𝒫𝒯 symmetry framework has been shown to be particularly adapted to find instabilities in high-dimensional parameter space (e.g. the drift wave instabilities in tokamaks; Qin et al. 2021). It has thus been demonstrated unequivocally that 𝒫𝒯-symmetric systems exhibit particular properties.
In this study, we aim to show that 𝒫𝒯 and anti-𝒫𝒯 symmetries also control some of the properties of the linear modes of astrophysical systems, such as instabilities, the absence of propagation, stability exchange, and the conservation of quadratic quantities, all acting in physical processes of different origins. We first define 𝒫𝒯 and anti-𝒫𝒯 symmetries in Sect. 2. We then demonstrate how they condition the outcome of the linear analysis of four canonical astrophysical systems, namely the self-gravity instability in discs (Sect. 3), wave propagation in gas–dust mixtures (Sect. 6), and buoyancy instability in stellar (Sect. 4) and planetary interiors (Sect. 5). We then discuss these analyses in a broader context of symmetric systems in Sect. 7.
2. Definitions
2.1. 𝒫𝒯 symmetry
The evolution of a monochromatic linear perturbation to the steady state of a fluid can be written under the form of an eigenvalue problem H(a)X = ωX, where the operator H that describes the evolution of the perturbation depends continuously on some real parameter a. The complex eigenvalues are generically denoted by the frequency ω, which can be a complex number a priori. This problem is said to be 𝒫𝒯 symmetric if there exists a unitary operator U such that
where * stands for complex conjugation. In this case, the eigenvalues form pairs: if ω is an eigenvalue of the problem, so is ω*. Indeed, HX = ωX implies H(U−1X*) = ω*(U−1X*). In 𝒫𝒯-symmetric systems, unstable modes are therefore accompanied by damped modes (imaginary parts of opposite sign). When ω ≠ ω*, 𝒫𝒯 symmetry is said to be spontaneously broken by H. By defining the symmetry operator 𝒫𝒯 ≡ UΘ, where Θ denotes complex conjugation, one has [𝒫𝒯, H] = 0. The two operators commute, but do not share X as an eigenvector for non-real eigenvalues.
Mostafazadeh (2002b,a) and Zhang et al. (2020c) showed that 𝒫𝒯 symmetry is equivalent to another symmetry, pseudo-Hermiticity, for finite-dimensional problems. A problem described by the operator H is pseudo-Hermitian if there exists a Hermitian operator V such that
where † denotes the Hermitian conjugate with respect to the appropriate Hermitian scalar product of the problem, which we will write ⋅ in the following, such that 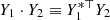 .
.
Let X1 and X2 be two eigenvectors of H satisfying Eq. (2). The eigenvalues ω1 and ω2 may take the same value: they degenerate. When the eigenvectors also become identical, the degeneracy is called an exceptional point (EP). The linear stability of these systems is described by Krein theory (Kreĭn 1950; Kirillov 2013): in such systems, the transition between stability and instability necessarily involves the exceptional degeneracy of stable eigenvalues. This phenomenon is known as a Krein collision. Before the collision, the system is stable, ω1 and ω2 are real, 𝒫𝒯 symmetry is said to be unbroken, and the Krein quantities defined as X1, 2 ⋅ VX1, 2 are non-zero and of opposite sign. After the collision, the system is unstable, the complex frequencies 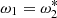 are complex conjugates of each other, and the two Krein quantities are necessarily zero. The Krein quantity Y ⋅ VY is a constant of motion of a general solution Y(t, a) of the evolution equation i∂tY = H(a)Y. Indeed,
are complex conjugates of each other, and the two Krein quantities are necessarily zero. The Krein quantity Y ⋅ VY is a constant of motion of a general solution Y(t, a) of the evolution equation i∂tY = H(a)Y. Indeed,
Hence,
Moreover, for a Fourier mode Y = e−iωtX, this conserved quantity is exactly zero for unstable and damped modes, and non-zero for propagative modes. This is shown by expressing
According to the identity above, a situation where ω ≠ ω* implies that X ⋅ VX = 0.
2.2. Anti-𝒫𝒯 symmetry
The eigenvalue problem H(a)X = ωX is said to be anti-𝒫𝒯-symmetric, or alternatively 𝒞𝒫-symmetric, if there exists a unitary operator 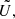 such that
such that
In this case, the eigenvalues come in pairs: ω and −ω*. They have equal imaginary parts, and opposite real parts and describe counter-propagating waves. In particular, H being anti-𝒫𝒯 symmetric is equivalent to iH being 𝒫𝒯 symmetric. The same equivalence between 𝒫𝒯 symmetry and pseudo-Hermiticity then applies, and guarantees that an anti-𝒫𝒯-symmetric operator H is also pseudo-chiral: there exist an Hermitian operator  such that
such that
The quantity 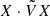 is not strictly a Krein quantity, and is not in general a constant of motion of a solution of i∂tX = HX. However, for a Fourier mode, Y = e−iωtX, one has
is not strictly a Krein quantity, and is not in general a constant of motion of a solution of i∂tX = HX. However, for a Fourier mode, Y = e−iωtX, one has
and is constant to zero for modes with Re(ω)≠0; that is, for modes that spontaneously break the anti-𝒫𝒯 symmetry. Indeed,
In summary, whenever ω ≠ −ω*, 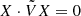 , the Krein quantity is zero at all times. An analogue of a Krein collision may occur. When the anti-𝒫𝒯 symmetry is unbroken, their exists a pair of eigenvalues of H, denoted ω1 and ω2, which are purely imaginary.
, the Krein quantity is zero at all times. An analogue of a Krein collision may occur. When the anti-𝒫𝒯 symmetry is unbroken, their exists a pair of eigenvalues of H, denoted ω1 and ω2, which are purely imaginary.
Let us consider the situation in which the parameter a passes through an EP, so that after the degeneracy we have 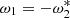 with non-zero real parts. Then, the anti-𝒫𝒯 symmetry is spontaneously broken. This phenomenon corresponds to a Krein collision for the operator iH. It follows that the quantity
with non-zero real parts. Then, the anti-𝒫𝒯 symmetry is spontaneously broken. This phenomenon corresponds to a Krein collision for the operator iH. It follows that the quantity 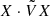 is non-zero and not conserved for non-propagative modes, and strictly zero for propagating modes for all times.
is non-zero and not conserved for non-propagative modes, and strictly zero for propagating modes for all times.
Systems that are both 𝒫𝒯 and anti-𝒫𝒯 symmetric are referred to as bisymmetric. The eigenvalues of bisymmetric systems take the form of (ω, −ω) pairs of real or purely imaginary frequencies. When ω is real, the associated eigenvector spontaneously breaks the anti-𝒫𝒯 symmetry. Conversely, when ω is imaginary, the associated eigenvector spontaneously breaks 𝒫𝒯 symmetry. Thus, one of those two symmetries is necessarily broken for any value of the parameters a, and either X ⋅ VX = 0 (broken 𝒫𝒯) or 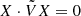 (broken anti-𝒫𝒯). In bisymmetric systems, X ⋅ VX is always a constant of motion, while
(broken anti-𝒫𝒯). In bisymmetric systems, X ⋅ VX is always a constant of motion, while 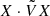 is constant only when it is zero, that is, in the spontaneously broken anti-𝒫𝒯 symmetry phase.
is constant only when it is zero, that is, in the spontaneously broken anti-𝒫𝒯 symmetry phase.
3. Gravitational instabilities
3.1. Jeans instability
The stability of self-gravitating objects plays a central role in the formation of structures throughout the Universe. The simplest problem to study would be the Jeans instability of a collapsing sphere (Jeans 1902). We consider local radial adiabatic perturbations of a 3D homogeneous self-gravitating, non-rotating, inviscid sphere of constant density ρ0 and sound speed cs. Linear perturbations of mass and momentum conservation combined with a Poisson equation form a 4 × 4 system that can be written after Fourier transforms in time and space:
This problem is invariant under both parity and time reversal. It is therefore trivially 𝒫𝒯 symmetric, as proven by the statement 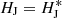 . As such, HJ is pseudo-Hermitian, with the symmetry operator
. As such, HJ is pseudo-Hermitian, with the symmetry operator 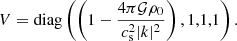 The Krein quantity associated to the Krein collision of the Jeans instability is then
The Krein quantity associated to the Krein collision of the Jeans instability is then 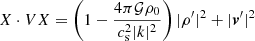 . This quantity is non-zero for propagating waves, and zero for the unstable modes. Complementarily, HJ is anti-𝒫𝒯 symmetric and pseudo-chiral; indeed, it satisfies Eq. (10) for
. This quantity is non-zero for propagating waves, and zero for the unstable modes. Complementarily, HJ is anti-𝒫𝒯 symmetric and pseudo-chiral; indeed, it satisfies Eq. (10) for 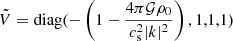 . The quantity
. The quantity 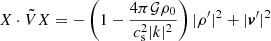 is then zero for propagative modes and non-constant and non-zero for unstable modes. The Krein collision occurs at an EP for which H cannot be diagonalised. This EP corresponds to marginal stability, which is reached at the Jeans wavenumber
is then zero for propagative modes and non-constant and non-zero for unstable modes. The Krein collision occurs at an EP for which H cannot be diagonalised. This EP corresponds to marginal stability, which is reached at the Jeans wavenumber 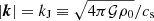 . Longer wavelengths are unstable, and shorter wavelengths are propagating.
. Longer wavelengths are unstable, and shorter wavelengths are propagating.
3.2. Toomre instability
More interesting is the case of a self-gravitating disc (Goodman & Narayan 1988; Goodman 2003; Bertin & Lodato 1999). In this system, 𝒫 and 𝒯 are broken individually, but the overall system of linear perturbations is still 𝒫𝒯 symmetric. Stabilisation of large and small scales by rotation and pressure can be sufficient to render astrophysical discs robust against gravitational collapse (Toomre 1964). Here we discuss the simplest case of axisymmetric perturbations of short radial wavelengths evolving in a razor-thin Keplerian disc. The stability of linear perturbations is given by the celebrated Toomre criterion: 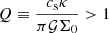 , where κ denotes the epicyclic frequency of the disc and Σ0 its surface density. The razor-thin disc is integrated vertically (Armitage 2010), to give the following set of radial linear perturbations:
, where κ denotes the epicyclic frequency of the disc and Σ0 its surface density. The razor-thin disc is integrated vertically (Armitage 2010), to give the following set of radial linear perturbations:
where we use perturbations of the enthalpy h′ and the two horizontal velocities 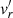 and
and 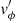 as variables, and the orbital time Ω−1 and the pressure length csΩ−1 as units of time and length.
as variables, and the orbital time Ω−1 and the pressure length csΩ−1 as units of time and length.
With U = diag(1, 1, −1), this problem satisfies Eq. (1) and is therefore 𝒫𝒯 symmetric. Rotation breaks the reflection symmetry in the azimuthal direction and the time reversal symmetry, but not the combination of both. The system is expected to be pseudo-Hermitian, which can be shown explicitly. With
the system satisfies Eq. (2). The Krein quantity associated with this 𝒫𝒯 symmetry provides the following energy partition, which applies to the unstable mode:
where k denotes the wavenumber in dimensional form. We illustrate this result by numerically computing the value of this quantity through a Krein collision, as Hsgd has degenerated eigenvalues when 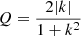 . These are the positions of EPs for Hsgd, which corresponds to positions of a Krein collision. The curve of EPs separates two regions in (Q, k) space: one is the stable region, and the other is the unstable region. Figure 1 shows the EP curve, as well as the Krein collision that occurs when crossing this curve.
. These are the positions of EPs for Hsgd, which corresponds to positions of a Krein collision. The curve of EPs separates two regions in (Q, k) space: one is the stable region, and the other is the unstable region. Figure 1 shows the EP curve, as well as the Krein collision that occurs when crossing this curve.
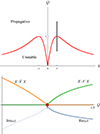 |
Fig. 1. 𝒫𝒯-symmetric properties of the Toomre instability. Top panel: Curve of EPs corresponding to marginal stability. A maximum is reached for Q = 1 as expected. Bottom panel: Krein collision of the stability of the Toomre problem when varying the parameters along the black line of the top panel. Depending on the value of Q, exactly one of the two Krein quantities identified is zero, depending on which symmetry is broken by the perturbation. The curve in green is X ⋅ VX, orange is |
In addition to being 𝒫𝒯 symmetric, Hsgd is also anti-𝒫𝒯 symmetric, because
with 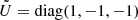 . The anti-𝒫𝒯 symmetry is complementary to the 𝒫𝒯 symmetry, and the combination of the two symmetries implies that the eigenvalues always come in pairs: they are always opposite (ω, −ω), either real or purely imaginary. They are never general complex numbers, which is a generic property for bisymmetric systems, as one of the two symmetries is necessarily spontaneously broken.
. The anti-𝒫𝒯 symmetry is complementary to the 𝒫𝒯 symmetry, and the combination of the two symmetries implies that the eigenvalues always come in pairs: they are always opposite (ω, −ω), either real or purely imaginary. They are never general complex numbers, which is a generic property for bisymmetric systems, as one of the two symmetries is necessarily spontaneously broken.
One has
Equation (20) explicitly shows that Hsgd is pseudo-chiral as expected, and Krein theory then applies. When iHsgd has real eigenvalues, anti-𝒫𝒯 symmetry is unbroken, and the Krein quantities 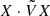 are non-zero. This holds when 𝒫𝒯 symmetry is spontaneously broken, that is, in the unstable region of parameters, where the first Krein quantity X ⋅ VX is zero. Conversely, in the stable range, anti-𝒫𝒯 symmetry is broken and 𝒫𝒯 symmetry is unbroken. In this case,
are non-zero. This holds when 𝒫𝒯 symmetry is spontaneously broken, that is, in the unstable region of parameters, where the first Krein quantity X ⋅ VX is zero. Conversely, in the stable range, anti-𝒫𝒯 symmetry is broken and 𝒫𝒯 symmetry is unbroken. In this case, 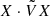 is zero and X ⋅ VX is not equal to zero. The Krein quantity
is zero and X ⋅ VX is not equal to zero. The Krein quantity 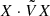 associated with the anti-𝒫𝒯 symmetry gives the following energy distribution for propagating waves in dimensional form:
associated with the anti-𝒫𝒯 symmetry gives the following energy distribution for propagating waves in dimensional form:
Hence, for each mode, either X ⋅ VX or 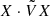 is necessarily zero: the former is zero for unstable modes and the latter is zero for propagating waves. Both are exactly zero at the degeneracy; that is, for ω = 0, which is true for
is necessarily zero: the former is zero for unstable modes and the latter is zero for propagating waves. Both are exactly zero at the degeneracy; that is, for ω = 0, which is true for 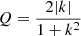 . Figure 1 shows this exchange in non-zero quantities when crossing the Krein collision. Krein quantities simply provide energy partitions of the system in both regimes.
. Figure 1 shows this exchange in non-zero quantities when crossing the Krein collision. Krein quantities simply provide energy partitions of the system in both regimes.
The matrices V and 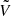 identified above are particular cases of more general families of matrices:
identified above are particular cases of more general families of matrices:
where a, b, and c are any real numbers such that detW ≠ 0. The matrix of Eq. (16) is recovered with  , b = 0, and
, b = 0, and 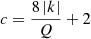 . Similarly,
. Similarly,
The matrix of Eq. (20) is recovered with 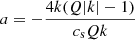 , b = 0, and
, b = 0, and 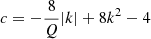 . The same holds for the different problems addressed in this study.
. The same holds for the different problems addressed in this study.
4. Buoyancy instability in stars
We now consider a non-rotating star in static equilibrium, balanced by thermal pressure and self-gravity. The steady state is spherically symmetric, and the density is stratified and decreases towards the surface. This equilibrium can be unstable, as a perturbation can be amplified by buoyancy if the square of the buoyancy frequency N2 is negative, as given by the Schwarzschild criterion (Schwarzschild 1906).
This problem was revisited by Leclerc et al. (2023) in inhomogeneous media, where the system proved to be pseudo-Hermitian and pseudo-chiral. Pseudo-Hermiticity was used to determine the Krein quantity. We now complete the picture by determining the Krein quantity associated to pseudo-chirality, and show the Krein collision in this bisymmetric problem.
Neglecting the self-gravity of the perturbations (Cowling’s approximation Cowling 1941), we start from Eq. (5) of Leclerc et al. (2023), which is the eigenvalue equation,
where ω is the complex eigenfrequency of the perturbation, and X ≡ (v w Θ p)⊤ contains the perturbation’s horizontal velocity, radial velocity, entropy, and pressure after appropriate rescaling. 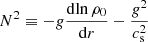 is the square of the buoyancy frequency, which is negative here,
is the square of the buoyancy frequency, which is negative here, 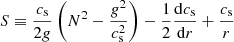 is another characteristic frequency called the buoyant-acoustic frequency, which quantifies the coupling between g-modes and p-modes in asteroseismic problems,
is another characteristic frequency called the buoyant-acoustic frequency, which quantifies the coupling between g-modes and p-modes in asteroseismic problems, 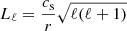 is the Lamb frequency, and Kr represents the local radial wavenumber of the wave (see Appendix E of Leclerc et al. 2023 for details).
is the Lamb frequency, and Kr represents the local radial wavenumber of the wave (see Appendix E of Leclerc et al. 2023 for details).
This problem is both pseudo-Hermitian and pseudo-chiral, and is associated with the two matrices:
Krein theory can therefore be applied to determine how discrete symmetries constrain the partition of energy. Here, X ⋅ X is generally not a conserved quantity, as Hb is not Hermitian; it grows exponentially for unstable modes and is conserved only for stable modes. However, X ⋅ VX is a constant of motion for any solution of ∂tX = HbX, as shown in Sect. 2.1. Moreover, this constant is exactly zero only for unstable modes. In contrast, 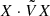 also grows exponentially for unstable modes, but is constantly equal to zero for stable modes. As such,
also grows exponentially for unstable modes, but is constantly equal to zero for stable modes. As such,
where δ is the Kronecker delta.
For the radial modes Lℓ = 0, the modes degenerate over the ring parameterised by 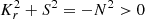 . These parameter values are EPs, as Hb can no longer be diagonalised there. The ring separates two ranges of parameters, the stable and the unstable part. Figure 2 shows the Krein quantities, over the ring of EPs in which the collision takes place. The Krein collision behaves as expected: inside the ring, the system is unstable, and X ⋅ VX is zero and
. These parameter values are EPs, as Hb can no longer be diagonalised there. The ring separates two ranges of parameters, the stable and the unstable part. Figure 2 shows the Krein quantities, over the ring of EPs in which the collision takes place. The Krein collision behaves as expected: inside the ring, the system is unstable, and X ⋅ VX is zero and 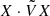 is non-zero. Outside the ring, the modes are stable and propagate as sound waves, and X ⋅ VX is non-zero and
is non-zero. Outside the ring, the modes are stable and propagate as sound waves, and X ⋅ VX is non-zero and 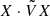 is zero.
is zero.
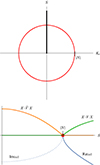 |
Fig. 2. Same as Fig. 1 but for the Schwarzschild instability. Non-hermiticity is broken in this case by buoyancy instead of self-gravity. |
This structure is equivalent to the bisymmetric problem of self-gravitating discs discussed in Sect. 3, and shown on Fig. 1, even if the physical situation is very different. The approach followed in this problem is the reverse of that followed in Section 3 for the Toomre problem: it is easier to first establish that the system is pseudo-Hermitian and pseudo-chiral, as the matrices V and 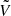 have ±1 on the diagonal.
have ±1 on the diagonal.
5. Rayleigh-Bénard instability
Not all instabilities correspond to spontaneous breaking of symmetries. The Rayleigh-Bénard instability (Bénard 1900; Rayleigh 1916) is such a case. Interiors of rocky planets are often treated as incompressible with both significant viscous and thermal diffusion (e.g. Bergé & Dubois 1984; Bodenschatz et al. 2000; Brandenburg 2021). This results in a regime of buoyancy instability that is controlled by diffusion effects and differs fundamentally from that discussed in Sect. 4 for adiabatic perturbations in compressible stars or planetary atmospheres. In the Rayleigh-Bénard regime, the instability criterion is given by the value of the Rayleigh number Ra = gαβL4/νκ, which needs to be greater than some critical value of order 102 − 103 depending on the boundary conditions. This famous problem admits analytical solutions for a homogeneous background configuration with rigid-lid isothermal boundary conditions, which provides us with an illustrative example of symmetries involving diffusive effects.
The basic set of equations consists of the incompressibility condition, a Navier-Stokes equation, and thermal heat diffusion for a 2D (x, z) fluid (see Appendix A). The x direction is invariant by translation and infinite, and the z direction is of length L, along which a constant temperature gradient ∂zT0 = −β is directed. With dimensionless variables, the problem for Fourier modes exp( − iωt + ikzz + ikxx) can be converted into the symmetrical form:
where Pr = ν/κ is the Prandtl number and 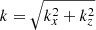 .
.
This problem is anti-𝒫𝒯 symmetric and pseudo-chiral, as one reads that
for Ra ≥ 0. In this case, the anti-𝒫𝒯 symmetry is protected and cannot be spontaneously broken as HRB is anti-Hermitian (i.e. iHRB is Hermitian). Indeed, the spectral theorem guarantees that the eigenvalues are purely imaginary and the eigenvectors are orthogonal to each other.
The location of EPs is given by
which requires that Ra be negative. This condition can only be fulfilled for an inverted temperature gradient, which corresponds to a stably stratified liquid. In this case, the anti-𝒫𝒯 symmetry is no longer protected and can be broken spontaneously, which would lead to propagating, damped internal waves.
Anti-Hermiticity ensures that the eigenvalues ω = iη are purely imaginary for all kx, kz, Ra, and Pr. The transition to instability is given by the change of sign, η < 0 to η > 0. This necessarily occurs for ω = 0, providing the marginal stability criterion for the Rayleigh-Bénard instability. This condition is satisfied when
whose minimum for each kx, kz compatible with the boundary conditions gives the critical value of the Rayleigh number (e.g. 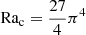 for stress-free, impenetrable, and isothermal boundaries). Figure 3 shows the regions of this problem.
for stress-free, impenetrable, and isothermal boundaries). Figure 3 shows the regions of this problem.
 |
Fig. 3. Different regions of the Rayleigh-Bénard problem in the parameter space. In the upper part Ra > 0, anti-𝒫𝒯 symmetry is protected, frequencies are purely imaginary, and the system exhibits an instability (black dashed) and no EPs. In the lower part Ra < 0, anti-𝒫𝒯 is no longer protected by anti-Hermiticity, and the system exhibits a curve of EP2s (red) delimiting a region where perturbations propagate. It is a region where anti-𝒫𝒯 symmetry is spontaneously broken. |
6. Waves in dusty mixtures
Mixtures of pressureless dust and inviscid non-magnetised gas are generically used to model basic hydrodynamical properties of the dusty interstellar medium (e.g. Saffman 1962; Baines et al. 1965; Ahuja 1973; Gumerov et al. 1988). Exchange of momentum between gas and dust is modelled as a drag force proportional to the difference between their velocities. The DUSTYWAVE problem consist of studying the propagation of a 1D acoustic wave in a homogeneous dusty medium. The question is whether small disturbances propagate or are simply attenuated, as both regimes are possible (e.g. Laibe & Price 2011; David-Cléris & Laibe 2021). The mixture is initially homogeneous and at rest. Looking for small perturbative solutions as Fourier modes exp(i(ωt − kx)), one obtains the eigenvalue equation
after appropriate rescaling and choice of dimensionless parameters, as described in Appendix B. The operator Hdw formally depends on two parameters: the wavenumber k and the dust density fraction of the mixture ϵ. Here, Hdw satisfies Eq. (9) with 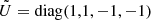 , meaning that Hdw is anti-𝒫𝒯 symmetric. This property stems from the reflection symmetry x ↦ −x of the fluid in physical space, as shown generically by David et al. (2022). Hence, the eigenvalues of Hdw are either imaginary or consist of pairs of complex numbers with opposite real parts. In parameter space, the transition between propagating and non-propagative regions must then be an EP at which the solution of two counter-propagating waves degenerates.
, meaning that Hdw is anti-𝒫𝒯 symmetric. This property stems from the reflection symmetry x ↦ −x of the fluid in physical space, as shown generically by David et al. (2022). Hence, the eigenvalues of Hdw are either imaginary or consist of pairs of complex numbers with opposite real parts. In parameter space, the transition between propagating and non-propagative regions must then be an EP at which the solution of two counter-propagating waves degenerates.
The characterisation of these EPs is carried out according to the procedure described in Delplace et al. (2021) (see Appendix C for details). Exceptional points of order 2 (or EP2s) are located on a 1D manifold in the parameter space (k, ϵ), which is a curve in a plane. Values of (k, ϵ) for which an eigenvalue has a multiplicity of two are characterised by the fact that the characteristic polynomial P(X) of Hdw has a root of multiplicity of two. Such a root is therefore also a root of its derivative P′(X), which means that the resultant R1 ≡ ℛ(P, P′) between the two polynomials is 0. The resultant between two polynomials only cancels out if they have a common root. As Hdw is anti-𝒫𝒯 symmetric, R1 is a real quantity. The values of (k, ϵ) for which R1 = 0 therefore define a curve. We calculate
and show the curve R1 = 0 (top panel, red) in Fig. 4. This curve provides a simple alternative derivation of the result of David-Cléris & Laibe (2021). Non-propagating waves exist for ϵ > 8/9, which is indeed the minimum of the curve of EPs.
 |
Fig. 4. Same as Fig. 1 but for the DUSTYWAVE problem. For k = 0.4, the Krein quantity |
Interestingly, in addition to the EP2s, the above method reveals the existence of third-order EPs for which three eigenvectors merge. These EP3s form a fold of dimension 0, which are two points in (k, ϵ) space. These two points are located at
which are the points at which the curve of the EP2s loses its regularity. At these EP3s, Hdw has only two eigenvectors corresponding to the two eigenvalues 0 and 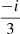 . We note that these EP3s carry topological charges, also called winding numbers W3:
. We note that these EP3s carry topological charges, also called winding numbers W3:
where EP31 is the point 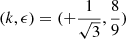 and EP32 is the point
and EP32 is the point 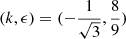 (see Appendix D). The question of connecting these topological charges to edge modes or particular global modes remains open (e.g. Leclerc et al. 2023).
(see Appendix D). The question of connecting these topological charges to edge modes or particular global modes remains open (e.g. Leclerc et al. 2023).
According to the discussion in Sect. 2.2, Hdw must be pseudo-chiral. The operator 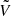 can be found explicitly
can be found explicitly
As has been shown, pseudo-chirality implies that if ω ≠ −ω*, the quantity 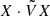 must be zero. This condition is fulfilled when sound propagates. Although the system is not conservative, it still possesses an associated Krein quantity
must be zero. This condition is fulfilled when sound propagates. Although the system is not conservative, it still possesses an associated Krein quantity 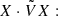
where ρ0 = ρg, 0 + ρd, 0 is the total background density. 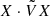 must be zero for propagating waves and non-zero for non-propagating waves. Figure 4 shows the numerical confirmation of this result.
must be zero for propagating waves and non-zero for non-propagating waves. Figure 4 shows the numerical confirmation of this result.  is only a constant of motion if it is zero, which is only the case for sound waves. Another technique, where the anti-𝒫𝒯 operator is diagonalised, can be used to extract constants of motion in the unbroken phase, as shown for the Kelvin-Helmholtz instability by Qin et al. (2019) (see Appendix E for details).
is only a constant of motion if it is zero, which is only the case for sound waves. Another technique, where the anti-𝒫𝒯 operator is diagonalised, can be used to extract constants of motion in the unbroken phase, as shown for the Kelvin-Helmholtz instability by Qin et al. (2019) (see Appendix E for details).
Finally, it should be noted that in a monofluid description of the mixture, the variables are ρ = ρg + ρd, v = ρgvg + ρdvd, 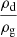 and Δv = vd − vg (Laibe & Price 2014). If the perturbed quantities are denoted by ′, the Krein quantity that cancels out for propagating perturbations is
and Δv = vd − vg (Laibe & Price 2014). If the perturbed quantities are denoted by ′, the Krein quantity that cancels out for propagating perturbations is
This quantity is associated with the symmetry operator
Squire & Hopkins (2018) show that when grains are additionally streaming though the gas, a generic resonant drag instability develops in the mixture. The system is neither 𝒫𝒯 nor anti-𝒫𝒯 symmetric and Krein theory cannot be applied directly. The instability comes from a more complex mechanism where a resonance occurs between an anti-𝒫𝒯 symmetric correction due to drag and a leading 𝒫𝒯 symmetric perturbation that arises from the streaming (e.g. Zhuravlev 2019; Magnan et al. 2024). Analysis of these problems from the point of view of discrete symmetries requires further specific study.
7. Gravitational instability of a dusty disc
To our knowledge, there are still no published theoretical predictions about what happens when systems with different discrete symmetries are combined. To illustrate this, we consider a final example, drawing on the analysis of Longarini et al. (2022), which deals with the gravitational instability of a dusty razor-thin disc. In the context of planet formation, the aim is to quantify the ways in which dust can favour the local collapse of gas or even clump itself into planetary embryos. This problem is a combination of the two problems presented in Sects. 3 and 6 and as such, is of order 6. With the notations used above, the matrix of linear perturbation in the local shearing box is
where Ω is the orbital frequency, B is the local Oort parameter, and cg and cd denote the sound speeds of the gas and dust, respectively. Time and lengths are rescaled to the stopping time ts and the stopping length cgts. The characteristic polynomial of the system is of order 5, meaning that the roots ω(k) cannot be determined analytically. In the regime of weak drag, Longarini et al. (2022) determines the marginal stability numerically.
On the other hand, this problem is 𝒫𝒯 symmetric, with the operator U = diag(−1, 1, 1, −1, 1, 1). The marginal stability curve is therefore a curve of EPs that corresponds to the spontaneous breaking of 𝒫𝒯 symmetry. From the analysis above, its exact expression is
a polynomial of high order with respect to the parameters of the problem. The explicit expression of Eq. (45) extends over two pages and is given in the worksheet in the Acknowledgements of the present paper. Hence, from a general perspective, the 𝒫𝒯-symmetric characterisation of a marginal stability criterion allows us to derive directly its analytical expression, albeit in a cumbersome manner, without approximations relying on asymptotically strong or weak drag regimes. Following Qin et al. (2021), this astrophysical example shows that the analysis of discrete symmetries therefore provides a powerful way to make analytical predictions about the marginal stability of symmetric systems with high dimensionalities (see Fig. 5).
 |
Fig. 5. Exceptional Points of the dusty self-gravitating disk are a consequence of the spontaneous breaking of 𝒫𝒯 symmetry. The equation R(P,P′) = 0 is obtained analytically with a resultant method, reproducing the results of Longarini et al. (2022). |
8. Conclusion
For several astrophysical objects, the properties of small perturbations around equilibrium are controlled by discrete symmetries, such as the 𝒫𝒯 symmetry and the anti-𝒫𝒯 symmetry. For example, we show that such symmetries are relevant in the following contexts:
-
The stability of isothermal spheres and thin self-gravitating discs: the Jeans and the Toomre problem are bisymmetric because of self-gravity.
-
The propagation of waves and the onset of convection in stratified fluids for compressible and adiabatic perturbations: the Schwarzschild problem is bisymmetric because of buoyancy.
-
The propagation of waves and the onset of convection in stratified fluids for incompressible and diffusive perturbations: the Rayleigh-Bénard problem is anti-𝒫𝒯 symmetric because of diffusion, and is also anti-Hermitian.
-
The propagation of a wave in a dust–gas mixture: the DUSTYWAVE problem is anti-𝒫𝒯 symmetric because of drag.
In these systems, the parameter space can be divided into different regions, in which the discrete symmetries are either broken or not. These regions are separated by exceptional points (EPs) for which the system of linear perturbation can no longer be diagonalised.
From a methodology perspective, the analysis of discrete symmetries allows – when relevant – the direct determination of physical quantities that may be harder to obtain alternatively:
-
The location of the EPs in the parameter space can be determined analytically from the symmetries without knowing the dispersion relation. This method is particularly effective for systems with high dimensions, where the dispersion relations may be untractable for analytical techniques, as in the case of the dusty self-gravitating disc.
-
Krein theory then makes it possible to directly determine the exchange of stability when EPs are crossed, as well as the partition of energy enforced by Krein invariants associated with the discrete symmetries, even for dissipative systems.
Some of these EPs can be of high order and carry topological charges; this is the case for the DUSTYWAVE problem. We note that not all physical systems allow such discrete symmetries. In particular, their spontaneous breaking is not a necessary condition for the system to be linearly unstable, as demonstrated by the Rayleigh-Bénard problem. We have focused here on the analysis of local stability, which applies to homogeneous systems. The study of global modes for inhomogeneous systems requires an extension of the Wigner-Weyl framework to non-Hermitian systems (e.g. Onuki 2020; Perez et al. 2021, 2022; Perez 2022; Leclerc et al. 2023).
Acknowledgments
We thank A. Venaille, P. Delplace, T. David–Cléris, E. Lynch, C. Longarini and S. Labrosse for stimulating discussions and comments. We thank the conference STAR@LYON for stimulation of this study. GL, AL and NP acknowledge the support of the European Research Council (ERC) CoG project PODCAST No. 864965. AL is funded by Contrat Doctoral Spécifique Normalien. We have used MATHEMATICA (Wolfram Research Inc. 2021), worksheets can be found at https://github.com/ArmandLeclerc/PTsymInAstroWaves.
References
- Ahuja, A. S. 1973, J. Appl. Phys., 44, 4863 [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation (Cambridge University Press) [Google Scholar]
- Baines, M., Williams, I., Asebiomo, A., & Agacy, R. 1965, MNRAS, 130, 63 [CrossRef] [Google Scholar]
- Bénard, H. 1900, Revue Gen. Sci. Pure Appl., 11, 1261 [Google Scholar]
- Bender, C. M., & Boettcher, S. 1998, Phys. Rev. Lett., 80, 5243 [CrossRef] [Google Scholar]
- Bender, C. M., Boettcher, S., & Meisinger, P. N. 1999, J. Math. Phys., 40, 2201 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, C. M., Brody, D. C., & Jones, H. F. 2002, Phys. Rev. Lett., 89, 270401 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, C. M., Brody, D. C., & Jones, H. F. 2004, Phys. Rev. D, 70, 025001 [NASA ADS] [CrossRef] [Google Scholar]
- Bergé, P., & Dubois, M. 1984, Contemp. Phys., 25, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, G., & Lodato, G. 1999, A&A, 350, 694 [NASA ADS] [Google Scholar]
- Bodenschatz, E., Pesch, W., & Ahlers, G. 2000, Ann. Rev. Fluid Mech., 32, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 2021, Lecture 4: Rayleigh-Bénard Problem http://norlx51.nordita.org/~brandenb/teach/AdvAstroFluids/4_Convection/notes.pdf [Google Scholar]
- Cowling, T. G. 1941, MNRAS, 101, 367 [NASA ADS] [Google Scholar]
- David, T. W., Delplace, P., & Venaille, A. 2022, Phys. Fluids, 34, 056605 [NASA ADS] [CrossRef] [Google Scholar]
- David-Cléris, T., & Laibe, G. 2021, MNRAS, 504, 2889 [CrossRef] [Google Scholar]
- Delplace, P., Yoshida, T., & Hatsugai, Y. 2021, Phys. Rev. Lett., 127, 186602 [CrossRef] [PubMed] [Google Scholar]
- El-Ganainy, R., Makris, K. G., Christodoulides, D. N., & Musslimani, Z. H. 2007, Opt. Lett., 32, 2632 [NASA ADS] [CrossRef] [Google Scholar]
- El-Ganainy, R., Makris, K. G., Khajavikhan, M., et al. 2018, Nat. Phys., 14, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, L., Xu, Y.-L., Fegadolli, W. S., et al. 2013, Nat. Mater., 12, 108 [CrossRef] [Google Scholar]
- Feng, L., Wong, Z. J., Ma, R.-M., Wang, Y., & Zhang, X. 2014, Science, 346, 972 [CrossRef] [Google Scholar]
- Feng, L., El-Ganainy, R., & Ge, L. 2017, Nat. Photonics, 11, 752 [CrossRef] [Google Scholar]
- Fu, Y., & Qin, H. 2020, New J. Phys., 22, 083040 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, Y., & Qin, H. 2024, Phys. Rev. Res., 6, 023273 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, L., & Türeci, H. E. 2013, Phys. Rev. A, 88, 053810 [CrossRef] [Google Scholar]
- Goodman, J. 2003, MNRAS, 339, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Narayan, R. 1988, MNRAS, 231, 97 [NASA ADS] [Google Scholar]
- Gumerov, N., Ivandaev, A., & Nigmatulin, R. 1988, J. Fluid Mech., 193, 53 [Google Scholar]
- Guo, A., Salamo, G. J., Duchesne, D., et al. 2009, Phys. Rev. Lett., 103, 093902 [CrossRef] [Google Scholar]
- Hodaei, H., Hassan, A. U., Wittek, S., et al. 2017, Nature, 548, 187 [CrossRef] [PubMed] [Google Scholar]
- Jeans, J. H. 1902, Philos. Trans. R. Soc. London Ser. A, 199, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirillov, O. N. 2013, Nonconservative Stability Problems of Modern Physics (de Gruyter) [CrossRef] [Google Scholar]
- Klaiman, S., Günther, U., & Moiseyev, N. 2008, Phys. Rev. Lett., 101, 080402 [NASA ADS] [CrossRef] [Google Scholar]
- Kreĭn, M. 1950, Dokl. Akad. Nauk SSSR A, 73, 445 [Google Scholar]
- Laibe, G., & Price, D. J. 2011, MNRAS, 418, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Laibe, G., & Price, D. J. 2014, MNRAS, 440, 2136 [Google Scholar]
- Leclerc, A., Jezequel, L., Perez, N., et al. 2023, The Exceptional Ring of buoyancy instability in stars [Google Scholar]
- Lin, Z., Ramezani, H., Eichelkraut, T., et al. 2011, Phys. Rev. Lett., 106, 213901 [NASA ADS] [CrossRef] [Google Scholar]
- Longarini, C., Lodato, G., Bertin, G., & Armitage, P. J. 2022, MNRAS, 519, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Magnan, N., Heinemann, T., & Latter, H. N. 2024, MNRAS, 529, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Makris, K. G., El-Ganainy, R., Christodoulides, D. N., & Musslimani, Z. H. 2008, Phys. Rev. Lett., 100, 103904 [CrossRef] [PubMed] [Google Scholar]
- Mostafazadeh, A. 2002a, J. Math. Phys., 43, 3944 [NASA ADS] [CrossRef] [Google Scholar]
- Mostafazadeh, A. 2002b, J. Math. Phys., 43, 205 [Google Scholar]
- Mostafazadeh, A., & Batal, A. 2004, J. Phys. A Math. General, 37, 11645 [NASA ADS] [CrossRef] [Google Scholar]
- Musslimani, Z. H., Makris, K. G., El-Ganainy, R., & Christodoulides, D. N. 2008, Phys. Rev. Lett., 100, 030402 [NASA ADS] [CrossRef] [Google Scholar]
- Onuki, Y. 2020, J. Fluid Mech., 883, A56 [Google Scholar]
- Özdemir, Ş. K., Rotter, S., Nori, F., & Yang, L. 2019, Nat. Materials, 18, 783 [CrossRef] [Google Scholar]
- Peng, B., Özdemir, Ş. K., Lei, F., et al. 2014, Nat. Phys., 10, 394 [CrossRef] [Google Scholar]
- Perez, N. 2022, Ph.D. Thesis, Ecole normale supérieure de lyon-ENS LYON [Google Scholar]
- Perez, N., Delplace, P., & Venaille, A. 2021, Proc. R. Soc. A, 477, 20200844 [CrossRef] [Google Scholar]
- Perez, N., Delplace, P., & Venaille, A. 2022, Phys. Rev. Lett., 128, 184501 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & King, A. 2007, Astrophysical Flows (Cambridge University Press) [Google Scholar]
- Qin, H., Fu, Y., Glasser, A. S., & Yahalom, A. 2021, Phys. Rev. E, 104, 015215 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, H., Zhang, R., Glasser, A. S., & Xiao, J. 2019, Phys. Plasmas, 26, 032102 [CrossRef] [Google Scholar]
- Rayleigh, L. 1916, Lond. Edinburgh Dublin Philos Mag. J. Sci., 32, 529 [Google Scholar]
- Regensburger, A., Bersch, C., Miri, M.-A., et al. 2012, Nature, 488, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Rüter, C. E., Makris, K. G., El-Ganainy, R., et al. 2010, Nat. Phys., 6, 192 [CrossRef] [Google Scholar]
- Saffman, P. 1962, J. Fluid Mech., 13, 120 [CrossRef] [MathSciNet] [Google Scholar]
- Schwarzschild, K. 1906, Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen Math.-phys. Klasse, 195, 41 [Google Scholar]
- Squire, J., & Hopkins, P. F. 2018, ApJ, 856, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Wolfram Research Inc. 2021, Mathematica, Version 13.0.0, champaign, IL. [Google Scholar]
- Zhang, F., Feng, Y., Chen, X., Ge, L., & Wan, W. 2020a, Phys. Rev. Lett., 124, 053901 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, H., Huang, R., Zhang, S.-D., et al. 2020b, Nano Lett., 20, 7594 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, R., Qin, H., & Xiao, J. 2020c, J. Math. Phys., 61, 012101 [Google Scholar]
- Zhuravlev, V. 2019, MNRAS, 489, 3850 [NASA ADS] [Google Scholar]
Appendix A: Rayleigh-Bénard: Linear perturbations
Here, we consider a two-dimensional fluid parametrised by the coordinates (x,z). The fluid is at rest in a constant gravity field g = −guz, and has constant density ρ0. The temperature profile has a constant gradient T(z) = Th − βz with β = (Th − Tc)/L. The coefficient of thermal expansion of the fluid is 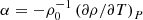 . The dynamical viscosity and thermal diffusivity of the fluid are denoted by ν and κ, respectively. The linear system describing the evolution of small perturbations in the Boussinesq approximation around this background state is
. The dynamical viscosity and thermal diffusivity of the fluid are denoted by ν and κ, respectively. The linear system describing the evolution of small perturbations in the Boussinesq approximation around this background state is
Applying double curl, and enforcing the incompressibility equation ∇ ⋅ v = 0, the equation for ux decouples from the other two equations, leaving
For plane wave solutions of the form exp( − iωt + ikzz + ikxx), Eqs. A.5 – A.6 become
Rescaling the time by L2/ν, the lengths by L and the temperature with βL leads to the introduction of the Rayleigh and Prandtl numbers, Ra = gαβL4/νκ and Pr = ν/κ. The following rescaling of the equations 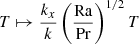 with
with  provides a system of eigenvalues that has the symmetric form
provides a system of eigenvalues that has the symmetric form
which corresponds to Eq.32. Consequently, iHRB is Hermitian if and only if Ra ≥ 0.
Appendix B: DUSTYWAVE: linear perturbations
Here, we consider a dusty mixture where gas and dust are treated as two fluids interacting with each other via a drag force. For pressureless dust in 1D, the equations for mass and momentum conservation are
where ρg, ρd denote the gas and the dust densities, vg, vd denote the gas and the dust velocities, and K is the drag coefficient. The mixture is initially homogeneous and at rest. We can write each quantity as a background and perturbation component f = f0 + f′. The system of equations can be put in a symmetric form using the rescaled quantities  . For isothermal pertubations
. For isothermal pertubations 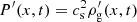 , the evolution of the perturbations are given by the system
, the evolution of the perturbations are given by the system
where 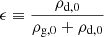 is the dust fraction, and
is the dust fraction, and  is the gas fraction. The barycentric stopping time
is the gas fraction. The barycentric stopping time 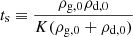 corresponds to the time needed for drag to damp the differential velocity between gas and dust. The stopping length csts is the typical spatial separation between the fluids. Using ts and csts as units of time and length, we obtain the dimensionless system
corresponds to the time needed for drag to damp the differential velocity between gas and dust. The stopping length csts is the typical spatial separation between the fluids. Using ts and csts as units of time and length, we obtain the dimensionless system
Appendix C: EPs from resultants
Here, we consider two polynomials Q1(X) and Q2(X) defined by
where αi and βj are their roots. The resultant ℛ(Q1, Q2) of these two polynomials is defined as
where S(Q1, Q2) is the Sylvester matrix of Q1 and Q2. It satisfies
which cancels if and only if Q1 and Q2 share a common root. The quantity (C.3) is determined by the coefficients ai, bj and does not require that we find the roots αi, βj. We can define P′, the derivative of P(X). The cancellation of the resultant R1 of P and P′ characterise the fact that P has a root with double multiplicity. In the context of this study, an EP of order at least 2 is the space formed by parameters for which
Appendix D: DUSTYWAVE: topological charges
In addition to EPs of order 2, the DUSTYWAVE is also found to have EPs of order 3. The structure of an EP3 is a fold of dimension 0, which is a point in the (k, ϵ) space. These points can be located using a procedure that generalises the determination of EP2s. Noting R1 = ℛ(P, P′) and R2 = ℛ(P, P″), the resultants of the characteristic polynomial and its derivatives, and EP3s correspond to points in the parameter space for which P, P, ′ and P″ have a common root. These points are those where both R1 and R2 cancel simultaneously. For the DUSTYWAVE problem, R1 is given by Eq. 38, and R2 by
Fig.D.1 shows the curves R1 = 0 (red) and R2 = 0 (blue). These curves cross four times, and two of these points are EP3s. They are located at
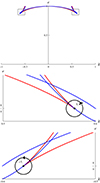 |
Fig. D.1. Exceptional points of the DUSTYWAVE in the parameter space (k, ϵ). Intersections between the red (R1 = 0) and blue (R2 = 0) curves indicate the positions of EP3s. The two bottom panels show zoomed-in images of two regions. The EP3s are marked by black points, with associated topological charge of ±1. |
For the other two points, P and P″ share a root different from the one shared by P and P′. As such, they are EP2s only. At the EP3s, H has two eigenvalues, 0 and  . It cannot be diagonalised, as it only has two eigenvectors,
. It cannot be diagonalised, as it only has two eigenvectors,
The EP3s have a non-zero topological charge, as defined in (Delplace et al. 2021). These topological invariants are defined as the winding numbers
for 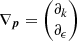 and
and 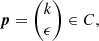 where C is any closed loop around one of the EP3s. We compute
where C is any closed loop around one of the EP3s. We compute
where EP31 is the point at 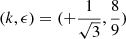 and EP32 is the point at
and EP32 is the point at  .
.
Appendix E: DUSTYWAVE: Anti-𝒫𝒯 operator
We define Θ as the operator of complex conjugation and 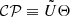 as the operator for anti-𝒫𝒯 symmetry. Equation (9) can be rewritten in the form
as the operator for anti-𝒫𝒯 symmetry. Equation (9) can be rewritten in the form
Equation E.1 constrains the phase between the components of the eigenvectors of Hdw, which are also called relations of polarisation. Here, we consider X0 an eigenvector of Hdw with pure imaginary eigenvalue. Formally,
where η0 is real. Applying the operator 𝒞𝒫 on Eq. E.2 and the commutation rule Eq.(E.1) gives the relation
If the eigenvalue is not degenerated (i.e. the parameters are chosen for the system not to be at an EP), 𝒞𝒫X0 is colinear to X0, i.e.
for some complex number α. Hence, Hdw and 𝒞𝒫 share the same eigenvectors and the anti-𝒫𝒯 symmetry is said to be unbroken. We note that the same reasoning applied to the operator iHdw shows that iHdw is 𝒫𝒯 symmetric. 𝒞𝒫 can be straightforwardly diagonalised. Its eigenvectors are
The condition given by Eq. E.4 therefore imposes the particular polarisation relations on non-propagating waves:
and other linear combinations of Eqs. E.6 – E.8. Therefore, the analysis of the discrete symmetries of the problem shows with a very small number of calculations that gas and dust densities are in phase, as are their velocities, while densities and velocities are in phase quadrature. Similar relations exist between fields in the unbroken 𝒫𝒯 symmetry phase of the Kelvin-Helmholtz problem discussed by Fu & Qin (2020).
This result can be reformulated with real fields. In the unbroken anti-𝒫𝒯 symmetry phase, the perturbations are damped without oscillating, and are of the form
which imposes that quantities be zero when they are spatially averaged. Formally, with
one obtains for example
for all times. On the contrary, in the phase where anti-𝒫𝒯 symmetry is broken, the frequency of the perturbations has a real part. Waves are propagating, and the polarisation relations are different from those in Eqs.(E.6)-(E.8), and the time-averages of quantities defined in Eqs. E.14 – E.15 are non-zero for this phase. Only propagating waves have non-zero macroscopic mass flux.
All Figures
 |
Fig. 1. 𝒫𝒯-symmetric properties of the Toomre instability. Top panel: Curve of EPs corresponding to marginal stability. A maximum is reached for Q = 1 as expected. Bottom panel: Krein collision of the stability of the Toomre problem when varying the parameters along the black line of the top panel. Depending on the value of Q, exactly one of the two Krein quantities identified is zero, depending on which symmetry is broken by the perturbation. The curve in green is X ⋅ VX, orange is |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but for the Schwarzschild instability. Non-hermiticity is broken in this case by buoyancy instead of self-gravity. |
| In the text | |
 |
Fig. 3. Different regions of the Rayleigh-Bénard problem in the parameter space. In the upper part Ra > 0, anti-𝒫𝒯 symmetry is protected, frequencies are purely imaginary, and the system exhibits an instability (black dashed) and no EPs. In the lower part Ra < 0, anti-𝒫𝒯 is no longer protected by anti-Hermiticity, and the system exhibits a curve of EP2s (red) delimiting a region where perturbations propagate. It is a region where anti-𝒫𝒯 symmetry is spontaneously broken. |
| In the text | |
 |
Fig. 4. Same as Fig. 1 but for the DUSTYWAVE problem. For k = 0.4, the Krein quantity |
| In the text | |
 |
Fig. 5. Exceptional Points of the dusty self-gravitating disk are a consequence of the spontaneous breaking of 𝒫𝒯 symmetry. The equation R(P,P′) = 0 is obtained analytically with a resultant method, reproducing the results of Longarini et al. (2022). |
| In the text | |
 |
Fig. D.1. Exceptional points of the DUSTYWAVE in the parameter space (k, ϵ). Intersections between the red (R1 = 0) and blue (R2 = 0) curves indicate the positions of EP3s. The two bottom panels show zoomed-in images of two regions. The EP3s are marked by black points, with associated topological charge of ±1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



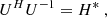
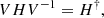
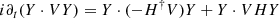
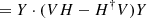
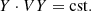
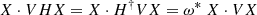
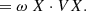
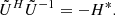
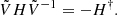
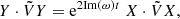
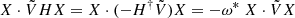
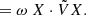
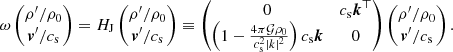
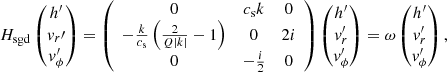
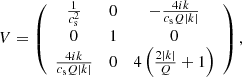
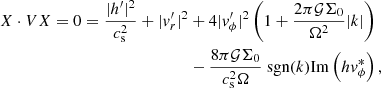
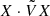

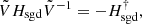
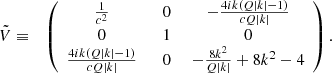
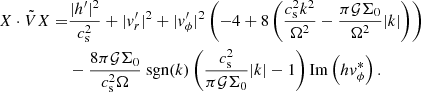
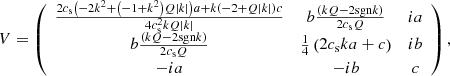
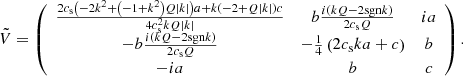
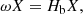
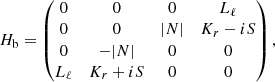
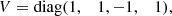
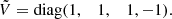
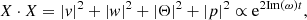
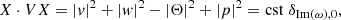
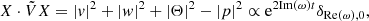
![$$ \begin{aligned}&\omega \begin{pmatrix} \tilde{{ v}_z}\\ [0.2cm] \tilde{T} \end{pmatrix} = H_{\rm RB} \begin{pmatrix} \tilde{{ v}_z}\\ [0.2cm] \tilde{T} \end{pmatrix},\end{aligned} $$](/articles/aa/full_html/2024/09/aa48710-23/aa48710-23-eq71.gif)