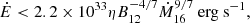| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202349033 | |
| Published online | 17 May 2024 | |
Probing the emission mechanism and nature of the pulsating compact object in the X-ray binary SAX J1324.4−6200
1
Institut für Astronomie und Astrophysik, Kepler Center for Astro and Particle Physics, University of Tuebingen, Sand 1, 72076 Tübingen, Germany
e-mail: ducci@astro.uni-tuebingen.de
2
ISDC Data Center for Astrophysics, Université de Genève, 16 chemin d’Écogia, 1290 Versoix, Switzerland
3
INAF – Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate (LC), Italy
4
INAF – OAR, Via Frascati, 33, 00078 Monte Porzio Catone, Rome, Italy
5
INAF – Osservatorio Astronomico di Cagliari, Via della Scienza 5, 09047 Selargius (CA), Italy
6
International Space Science Institute, Hallerstrasse 6, 3012 Bern, Switzerland
7
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received:
20
December
2023
Accepted:
1
March
2024
Recently, there has been renewed interest in the Be X-ray binary (Be/XRB) SAX J1324.4−6200 because of its spatial coincidence with a variable γ-ray source detected by Fermi/LAT. To explore more thoroughly its properties, new X-ray observations were carried out in 2023 by NuSTAR, XMM-Newton, and Swift satellites, jointly covering the energy range from 0.2 − 79 keV. SAX J1324.4−6200 was caught at an X-ray flux of ∼10−11 erg cm−2 s−1. The X-ray spectrum fits well with an absorbed power law with a high energy cutoff. Other acceptable fits require an additional blackbody component (kTbb ≈ 1.1 keV) or a Gaussian in absorption (Egabs ≈ 6.9 keV). We measured a NuSTAR spin period of 175.8127 ± 0.0036 s and an XMM-Newton spin period of 175.862 ± 0.025 s. We show that all the available spin period measurements of SAX J1324.4−6200, spanning 29 yr, are highly correlated with time, resulting in a remarkably stable spin-down of Ṗ = 6.09 ± 0.06 × 10−9 s s−1. We find that if SAX J1324.4−6200 hosts an accretion-powered pulsar, accretion torque models indicate a surface magnetic field of ∼1012 − 13 G. The X-ray properties emerging from our analysis strenghten the hypothesis that SAX J1324.4−6200 belongs to the small group of persistent Be/XRBs. We also performed radio observations with the Parkes Murriyang telescope, to search for radio pulsations. However, no radio pulsations compatible with the rotational ephemeris of SAX J1324.4−6200 were detected. We rule out the hypothesis that SAX J1324.4−6200 is a γ-ray binary where the emission is produced by interactions between the pulsar and the companion winds. Other models commonly used to account for the production of γ-rays in accreting pulsars cannot reproduce the bright emission from SAX J1324.4−6200. We examined other possible mechanisms behind the γ-ray emission and note that there is a ∼0.5% chance probability that an unknown extragalactic active galactic nucleus (AGN) observed through the Galactic plane may coincidentally fall within the Fermi/LAT error circle of the source and be responsible for the γ-ray emission.
Key words: accretion, accretion disks / stars: magnetars / stars: neutron / gamma rays: stars / X-rays: binaries / X-rays: individuals
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
SAX J1324.4−6200 was discovered in 1997 with BeppoSAX (Angelini et al. 1998). Then, it was observed by ASCA (Angelini et al. 1998; Lin et al. 2002), Swift (Mereghetti et al. 2008), Chandra, and XMM-Newton (Kaur et al. 2009). It was never observed in X-rays at energies above 10 keV until 2023. SAX J1324.4−6200 was classified as a likely Be/X-ray binary (Be/XRBs, a subclass of high mass X-ray binaries; for a review, see Reig 2011) at a distance in the range of 1.5–15 kpc, based on two photometric analyzes (Mereghetti et al. 2008; Kaur et al. 2009). No Gaia DR3 counterpart is catalogued within the Chandra 3σ error region (Gaia Collaboration 2023). SAX J1324.4−6200 hosts a pulsar with a spin period of Pspin ≈ 173 s (Angelini et al. 1998). Since its discovery, it has shown a constant spin-down with rate of Ṗ ≈ 6 × 10−9 s s−1 (Kaur et al. 2009). A tentative detection of an orbital period at ≈27 h was reported by Lin et al. (2002) in an ASCA observation. However, some doubts about this periodicity were raised by the same authors, who pointed out that the detection was based on only two cycles of the period, and the folded light curve had a suspicious non-smoothed shape (see, also, the discussion in Mereghetti et al. 2008). The 1 − 10 keV flux has not so far shown large variability, always being ≈0.5 − 1 × 10−11 erg cm−2 s−1. The X-ray spectrum has been described by an absorbed power law, with NH ≈ 5 × 1022 cm−2 and a photon index ∼1.25 (Angelini et al. 1998; Lin et al. 2002; Mereghetti et al. 2008; Kaur et al. 2009).
The steady and relatively low X-ray luminosity of SAX J1324.4−6200 (≈1033 − 35 erg s−1, assuming 1.5 ≲ d ≲ 15 kpc) is compatible with those displayed by the small subgroup of persistent Be/XRB pulsars (Pfahl et al. 2002), the best-known member of which is X Persei. The relatively faint and stable X-ray emission of these sources is thought to be due to the wide and circular neutron star (NS) orbit (Porb ≫ 30 d, e < 0.2) and accretion of the NS from the low-density polar wind of the companion star (see, e.g., Mereghetti et al. 2008; Reig & Roche 1999; La Palombara & Mereghetti 2007; La Palombara et al. 2021, and references therein).
The nature of SAX J1324.4−6200 as an accreting NS was thought to be settled until Harvey et al. (2022) reported the discovery of a persistent γ-ray emission over 12.5 yr of Fermi/LAT data from a region consistent with the position of SAX J1324.4−6200. In addition, they find evidence of variability in the γ-ray source, with relatively higher γ-ray emission over an 18-month period in 2018 and 2019. They rule out this emission being caused by other already catalogued γ-ray sources in the vicinity of SAX J1324.4−6200. There are no γ-ray pulsars in the third Fermi/LAT catalog associated with SAX J1324.4−6200 (Smith et al. 2023), nor other X-ray binaries (Avakyan et al. 2023; Neumann et al. 2023; Fortin et al. 2023, 2024), nor other bright X-ray sources (search performed in Vizier1). The source has no associated persistent radio emission (Harvey et al. 2022). Taking into account only the photons detected during the 2018–2019 bright event, Harvey et al. (2022) find that the γ-ray source has an offset from SAX J1324.4−6200 of ∼0.07°, well within the 95% containment radius (∼0.19°). They conclude that the 18-month excess is spatially coincident with SAX J1324.4−6200. The γ-ray source was bright enough to allow spectral analysis. Harvey et al. (2022) find that the best-fitting model is a power law with spectral index −2.43, and that the 100 MeV−500 GeV flux is ∼2.98 × 10−6 MeV cm−2 s−1. Harvey et al. (2022) point out that if the γ-ray emission is associated with SAX J1324.4−6200, it could be produced by the collision between the winds from the pulsar and the companion star, similar to what has been proposed for some γ-ray binaries (see, e.g., Dubus 2013; Paredes & Bordas 2019; Dubus et al. 2017; Chernyakova & Malyshev 2020, and references therein). This hypothesis was supported by the γ-ray luminosity and spectral index measured by Harvey et al. (2022), which are consistent with those of other γ-ray binaries with pulsars (see, e.g., Dubus 2013). This scenario casts serious doubts on accretion being the mechanism that explains the X-ray emission from SAX J1324.4−6200, as was previously accepted.
In light of these recent findings, we gathered more information about SAX J1324.4−6200, to understand its nature. Here, we report on the analysis of X-ray observations of SAX J1324.4−6200 spanning the 0.2–79 keV band and carried out in 2023 with NuSTAR, XMM-Newton, and Swift. To gain further insights, an observation was also performed with the Parkes Murriyang telescope in search of radio pulsations. Then, we discuss the nature of SAX J1324.4−6200 using the results of our X-ray and radio data analysis together with the other information available for this source.
2. Data analysis
2.1. NuSTAR
The Nuclear Spectroscopic Telescope Array (NuSTAR) satellite is equipped with two identical co-aligned telescopes with focal plane modules FPMA and FPMB. Both operate in the 3−79 keV energy band (Harrison et al. 2013). NuSTAR observed SAX J1324.4−6200 from 1 to 3 July, 2023, for a net exposure time of about 62 ks (see Table 1). Data were reduced using NUSTARDAS v2.1.2, which is part of HEASOFT v6.32.1, and the calibration files distributed with CALDB v20230802 (Madsen et al. 2022). We extracted the source events from a circular region centered on it and with a radius of 87″ and 75″ for FPMA and FPMB, respectively. These radii were calculated to have the maximum signal-to-noise ratio, with the constraint to keep the extraction area within the same detector (Det-0). For the background, we extracted the events from circular regions located on the same detector of the source (Det-0) but in a zone of the focal plane free from the emission of SAX J1324.4−6200. Event times were corrected from satellite frame to the Solar System barycenter using the ephemeris JPLEPH.200 and the barycorr task. The spectra were rebinned using the optimal binning method of Kaastra & Bleeker (2016) and made to have at least 25 counts per bin to enable the use of the χ2 as the fit statistic. This variation of the Kaastra & Bleeker (2016) technique was implemented in the HEASOFT tool ftgrouppha.
Summary of the X-ray observations.
2.2. XMM-Newton
The X-ray Multi-Mirror Mission (XMM-Newton) hosts the European Photon Imaging Camera (EPIC). It comprises the pn and two metal-oxide semiconductor (MOS) charge-coupled devices (CCDs), MOS1 and MOS2, operating in the 0.2−12 keV energy band (Jansen et al. 2001; Strüder et al. 2001; Turner et al. 2001). XMM-Newton observed SAX J1324.4−6200 on July 12, 2023 (see Table 1). We reduced the data using the XMM-Newton Science Analysis System (SAS, v21.0.0), with the latest calibration files available in the XMM-Newton calibration database (CCF). Calibrated event lists for the pn, MOS1, and MOS2 were obtained from the raw data with the SAS tasks epproc and emproc. For the pn, we used single- and double-pixel events, while for the MOS data we used single- to quadruple-pixel events. We excluded time intervals where the background was too high for a meaningful spectral analysis using the standard procedures2. The net exposure times obtained for the XMM-Newton observation are reported in Table 1. Source events were extracted using circular regions centered on the best-known position of SAX J1324.4−6200. The radii of these extraction regions were rpn = 36.45″, rMOS1 = 50″, and rMOS2 = 51″. These radii were calculated with the SAS task eregionanalyse to have the maximum signal-to-noise ratio. Background events were accumulated for each of the three cameras using extraction regions in the same CCD in which SAX J1324.4−6200 is located and not contaminated by its emission. The effective area of the pn, MOS1, and MOS2 were corrected in accordance with the CCF Release Note XMM-CCF-REL-3883 to improve the alignment with the NuSTAR spectra. Event times were corrected from the satellite frame to the Solar System barycenter using the ephemeris DE200 and the SAS task barycen. The spectra were rebinned with the tool ftgrouppha using the optimal binning method and made to have at least 25 counts per bin in order to enable the use of the χ2 as the fit statistic.
2.3. Swift X-ray Telescope
SAX J1324.4−6200 was observed by the X-ray Telescope (XRT, 0.3–10 keV) on board the Neil Gehrels Swift Observatory on July 1, 2023 for about 5.4 ks (see Table 1). The data were processed using the standard software (HEASOFT v6.31) and calibration (CALDB v20230725). Swift/XRT data were filtered with the task xrtpipeline (v0.13.7). No pileup correction was necessary. We extracted the source and background events for the spectral analysis with xselect. For the source, we used a circular extraction region centered on the source with a radius of 18 pixels, while the background was extracted from an annular region centered on the same position, with inner and outer radii of 60 and 100 pixels. The instrumental channels were combined to include at least 20 photons per bin using the grppha task.
2.4. Murriyang
SAX J1324.4−6200 was observed with the Ultra Wideband Low (UWL, Hobbs et al. 2020) receiver of the Murriyang radio telescope (Parkes, NSW, Australia) on March 30, 2023 for three hours. The data were recorded over the entire 3384 MHz bandwidth of the UWL receiver centered on a frequency of 2368 MHz. The bandwidth was split into 1-MHz wide channels, which were 8-bit sampled every 1.024 ms, and only total intensity information was recorded.
The data were folded with the dspsr4 (van Straten & Bailes 2011) pulsar package using the rotational ephemeris derived in this paper from the X-ray observations (see Sect. 3.1) and with a dispersion measure (DM) of 370 pc cm−3. This initial DM was derived as the median between the minimum and maximum values obtained using the 1.5–15 kpc distance range mentioned above and the NE2001 and YMW16 models for the distribution of the electrons in the interstellar medium (Cordes & Lazio 2002; Yao et al. 2017). Given the extremely long period of the pulsar, the dispersive delay is negligible even in the worst case of a true DM being double the maximum predicted by the electron density models (1600 pc cm−3, in which case the dispersive delay across the band would be about 14 s; that is, less than 1/10 of the pulsar period). Notwithstanding this, we searched the data over a DM range from 0 to 1600 pc cm−3 to maximise the signal-to-noise ratio of a possible pulsed emission. This DM search was done jointly with a spin period search spanning ±350 ms around the nominal period predicted at the epoch of the radio observations using the X-ray ephemeris. This was carried out with pdmp from the software package psrchive5 (Hotan et al. 2004; van Straten et al. 2012).
3. Results
3.1. Timing and variability analysis
The NuSTAR data (modules A and B) and the XMM-Newtonpn data were used for the timing analysis. The source and background events were extracted from the same regions adopted for the spectral extraction. We searched for the spin period in the 0.2 − 12 keV events of pn and in the 3 − 60 keV combined events of modules A and B of NuSTAR, using a Rayleigh test, Z2, with three harmonics (see, e.g., Buccheri et al. 1983). We refined the measurement of the detected signal using the phase-fitting method (see, e.g., Dall’Osso et al. 2003). Using this technique, we measured a NuSTAR spin period of Pspin, NuSTAR = 175.8127 ± 0.0036 s and an XMM-Newton spin period of Pspin, XMM = 175.862 ± 0.025 s (see Table 2). The XMM-Newton period is consistent with the NuSTAR measurement at a confidence level of ∼1.97σ. We fit all the previous and our new measured values of the spin period (Angelini et al. 1998; Lin et al. 2002; Mereghetti et al. 2008; Kaur et al. 2009) with the linear relation P(t) = P0 + Ṗt. The data are highly correlated: the Pearson’s linear coefficient is r = 0.9998, and the null hypothesis probability is 1.7 × 10−9 (see Fig. 3). We obtained a spin period derivative of Ṗ = 6.09 ± 0.06 × 10−9 s s−1. The ASCA (Lin et al. 2002) and our recent NuSTAR spin period measurement are outliers from the general trend shown in Fig. 3. They could indicate the sporadic occurrence of small fluctuations in the accretion torque rate, or they might be caused by systematic effects in the spin determination. To produce the light curves, the events were rebinned with a time resolution of 0.2 s for pn and 0.5 s for NuSTAR. The final light curves were then created by subtracting the background. We folded the NuSTAR and pn light curves using their respective spin periods. The pulse profiles, for different energy bands, are shown in Figs. 1 and 2. We selected these energy bands to have a similar number of average counts. For each pulse profile, we calculated the pulsed fraction using the formula
Measurement of the spin period in the NuSTAR and XMM-Newton observations analyzed in this work.
 |
Fig. 1. XMM-Newton pulse profiles of SAX J1324.4−6200 for three energy bands (ϕ = 0 at T0 = 60125.999592912 MJD). |
 |
Fig. 2. NuSTAR pulse profiles of SAX J1324.4−6200 for three energy bands (ϕ = 0 at T0 = 601265.0 MJD). |
 |
Fig. 3. Long-term evolution of the spin period of SAX J1324.4−6200 including the 1994 and 2000 ASCA observations, the 1997 BeppoSAX observation, the 2008 and 2023 XMM-Newton observations, the 2008 Swift observation, and the 2023 NuSTAR observation. The best-fitting linear model is shown (blue line). The bottom panel shows the residuals. |
where Rmax and Rmax are the maximum and minimum values of the rates (c/s) of the folded light curves. The measured values of pf are in Table 3.
We investigated the short-term spectral variability using the hardness ratios (HRs). The HRs were defined as counts in the hard band divided by counts in the soft band, H/S, where the energy bands are: S = 0.2 − 5.2 keV and H = 5.2 − 12 keV for XMM-Newton, and S = 3 − 9 keV and H = 9 − 60 keV for NuSTAR. The bin times were defined as three times the spin period. Figure 4 does not show any significant variability in hardness within each observation.
 |
Fig. 4. Left panel: XMM-Newton light curves (S = 0.2 − 5.2 keV and H = 5.2 − 12 keV) and HRs as a function of time (bintime = 527.586 s). Right panel: NuSTAR light curves (S = 3 − 9 keV and H = 9 − 60 keV) and HRs as a function of time (bintime = 527.4381 s). |
3.2. Spectral analysis
Swift/XRT and NuSTAR data were collected during overlapping periods, while the XMM-Newton observation was made after 11 days. To investigate possibly significant spectral variability between the two different data collection periods, and to verify that all the spectra could be fit simultaneously, we proceeded as follows. First, we fit simultaneously Swift/XRT and NuSTAR data and afterwards XMM-Newton data (pn, MOS1, and MOS2). In the first case (XRT+NuSTAR), we obtained an acceptable fit with an absorbed power law with a high energy cutoff (po*highecut in XSPEC6). To model the photoelectric absorption, we used the tbabs model in XSPEC and we set the abundances to those of the interstellar medium (wilm in XSPEC; Wilms et al. 2000). Constant renormalization factors were included in the spectral fitting to account for intercalibration uncertainties between instruments. Due to the limited energy coverage of the XMM-Newton spectra, they were insensitive to the high-energy-cutoff parameters. To investigate possible spectral variability in the soft part of the XMM-Newton spectrum with respect to XRT+NuSTAR data, we froze Ec and Ef to the values found from the XRT+NuSTAR best fit. The results are shown in Table 4 and Fig. 5. A close look at the best fit parameters in Table 4 shows that NH and Γ from the XRT+NuSTAR fit are slightly different compared to those from XMM-Newton. However, a comparison of the contour plots of Γ versus NH (Fig. 8) shows that these parameters are consistent between the two fits within ≲2σ. The reduced χ2 of the XRT+NuSTAR and XMM-Newton cases are suspiciously high (XRT+NuSTAR: 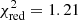 ; XMM-Newton:
; XMM-Newton: 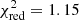 ). Therefore, we rebinned the spectrum for the purpose of visual inspection only, to improve the clarity of the residuals panel. This rebinning, obtained using setplot rebin in XSPEC, does not affect the results of the spectral fitting, which were obtained using the original binned spectrum. Using this approach, the new residual panels (see Fig. 6) show a wave-like structure between ∼3 keV and ∼20 keV, with a minimum at ∼7 keV. Given the general agreement between the best fit parameters obtained from these two fits, we decided to fit all datasets simultaneously to further improve the statistics. To explore possibly better descriptions of the observed spectrum, we tried to fit it with physical models typically used for accreting NSs in Be/XRBs: a power law with a Fermi–Dirac cutoff (fdcut, Tanaka 1986), the negative-positive exponential model (npex, Mihara 1995), Comptonization of soft photons in a hot plasma (comptt, Titarchuk 1994), and double comptt (see, e.g., Doroshenko et al. 2012). All these models give similar or worse χ2/d.o.f. than po*highecut, and no substantial improvement in the residuals.
). Therefore, we rebinned the spectrum for the purpose of visual inspection only, to improve the clarity of the residuals panel. This rebinning, obtained using setplot rebin in XSPEC, does not affect the results of the spectral fitting, which were obtained using the original binned spectrum. Using this approach, the new residual panels (see Fig. 6) show a wave-like structure between ∼3 keV and ∼20 keV, with a minimum at ∼7 keV. Given the general agreement between the best fit parameters obtained from these two fits, we decided to fit all datasets simultaneously to further improve the statistics. To explore possibly better descriptions of the observed spectrum, we tried to fit it with physical models typically used for accreting NSs in Be/XRBs: a power law with a Fermi–Dirac cutoff (fdcut, Tanaka 1986), the negative-positive exponential model (npex, Mihara 1995), Comptonization of soft photons in a hot plasma (comptt, Titarchuk 1994), and double comptt (see, e.g., Doroshenko et al. 2012). All these models give similar or worse χ2/d.o.f. than po*highecut, and no substantial improvement in the residuals.
Best-fit spectral parameters from the simultaneous fit of the Swift/XRT and NuSTAR (XRT+NuSTAR) and XMM-Newton data sets with an absorbed power law with a high energy cutoff, and constant renormalization factors.
 |
Fig. 5. Left panel: NuSTAR (black: module A; red: module B) and Swift/XRT (green) spectra of SAX J1324.4−6200, fit simultaneously with an absorbed power law with a high energy cutoff. Right panel: XMM-Newton (black: pn; red: MOS1; green: MOS2) spectra of SAX J1324.4−6200, fit simultaneously with an absorbed power law with a high energy cutoff (Ec and Ef frozen to the best fit values obtained from the XRT+NuSTAR fit). The lower panels show the residuals of the fit. |
 |
Fig. 6. Same spectra as in Fig. 5, rebinned using setplot rebin in XSPEC, and thus for plotting purposes only, to better visualize the wave-like shape of the residuals. |
Therefore, we tried to get a better fit by adding new components to the base model po*highecut. We obtained better fits, both for χ2/d.o.f. and for the residuals, by adding a blackbody component or a Gaussian in absorption. The results of these fits are shown in Table 5 and Fig. 7. In Table 5, the cross-normalization constants of the XMM-Newton instruments with respect to NuSTAR reflect the slightly lower X-ray flux of SAX J1324.4−6200 during the XMM-Newton observation (see Table 4). To evaluate the probability of improving the fit by adding the blackbody or a Gaussian in absorption component, we simulated, for each case, 5 × 104 datasets without the extra components using the XSPEC routine simftest (see, e.g., Ducci & Malacaria 2022, and references therein). We found that the probability that the observed data are consistent with the model without the extra component is < 0.002% in both the cases of a Gaussian in absorption and the blackbody as extra components. The radius of the blackbody component ranges between ∼0.07 km and ∼0.7 km, depending on the distance of the source (d = 1.5 − 15 kpc). The blackbody emission could be interpreted as the thermal radiation from a hot X-ray spot on the NS surface. In the other case, the Gaussian in absorption could be interpreted as a cyclotron resonance scattering feature (CRSF). In this case, using the law Ecyc ≈ 11.6B12 (keV) (e.g., Staubert et al. 2019), which links the centroid energy of the fundamental CRSF with the magnetic field strength of the pulsar (B12 is the magnetic field strength in units of 1012 G), we infer a NS surface magnetic field strength of B ≈ 6 × 1011 G.
Best-fit spectral parameters for the simultaneous fit of the Swift/XRT, NuSTAR, and XMM-Newton spectra with three different models.
 |
Fig. 7. XMM-Newton (black: pn; red: MOS1; green: MOS2), NuSTAR (blue: module A; cyan: module B), and Swift/XRT (orange) spectra of SAX J1324.4−6200 (rebinned using setplot rebin in XSPEC). Top panel: Spectra were fit simultaneously with an absorbed power law with a high energy cutoff and a Gaussian in absorption at ∼6.9 keV. Second panel: Residuals relative to the top panel. Third panel: Residuals of the fit of the spectra with an absorbed power law with a high energy cutoff and a blackbody. Bottom panel: Residuals of the fit of the spectra with an absorbed power law with a high energy cutoff. Table 5 lists the best fit parameters. |
3.3. Radio pulsation search
No radio pulsations compatible with the rotational ephemeris of SAX J1324.4−6200 were found in the Murriyang data. The non-detection can be used to calculate an upper limit of the pulsed flux density of the pulsar. We did so using the radiometer equation adapted for pulsars (see, e.g., Lorimer & Kramer 2004), adopting a system temperature of 21 K, an antenna gain of 0.735 K Jy−1, using a pulse duty cycle of 10%, and a signal-to-noise ratio of eight. With such parameters, we find that SAX J1324.4−6200 must have a radio pulsed mean flux density lower than 9 μJy.
4. Discussion
4.1. γ-ray binary scenario
We begin by considering the scenario proposed by Harvey et al. (2022): SAX J1324.4−6200 is a γ-ray binary, where the accretion is turned off and the observed emission is produced by the collision of the pulsar wind with the stellar wind of the companion star. In γ-ray binaries, most of the rotational energy of the pulsar is thought to be carried away by the pulsar wind, and a fraction of this energy is released as radiation when this wind interacts with the outflow from the companion star. The loss of rotational energy from the pulsar is therefore the energy reservoir that is used to produce the observed radiation (see, e.g., Dubus 2013). This can be estimated as 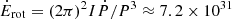 erg s−1, where I is the NS moment of inertia calculated assuming MNS = 1.4 M⊙ and RNS = 12 km, and where we adopted the spin period, P, detected with NuSTAR and the spin period derivative, Ṗ, obtained using all the X-ray observations of SAX J1324.4−6200 (Sect. 3.1). The distance of SAX J1324.4−6200 is in the range of 1.5–8 kpc or 5–15 kpc, according to Kaur et al. (2009) and Mereghetti et al. (2008), respectively. Therefore, given an observed 0.2–60 keV unabsorbed flux of ∼1.8 × 10−11 erg cm−2 s−1, the observed X-ray luminosity (Lx, obs ≈ 4.8 − 480 × 1033 erg s−1) exceeds the spin-down energy loss by orders of magnitude, ruling out the colliding winds mechanism as the origin of the source emission.
erg s−1, where I is the NS moment of inertia calculated assuming MNS = 1.4 M⊙ and RNS = 12 km, and where we adopted the spin period, P, detected with NuSTAR and the spin period derivative, Ṗ, obtained using all the X-ray observations of SAX J1324.4−6200 (Sect. 3.1). The distance of SAX J1324.4−6200 is in the range of 1.5–8 kpc or 5–15 kpc, according to Kaur et al. (2009) and Mereghetti et al. (2008), respectively. Therefore, given an observed 0.2–60 keV unabsorbed flux of ∼1.8 × 10−11 erg cm−2 s−1, the observed X-ray luminosity (Lx, obs ≈ 4.8 − 480 × 1033 erg s−1) exceeds the spin-down energy loss by orders of magnitude, ruling out the colliding winds mechanism as the origin of the source emission.
4.2. Non-accreting magnetar scenario
Retaining the non-accretion scenario considered in Sect. 4.1, the magneto dipole formula for pulsars (see, e.g., Manchester & Taylor 1977) provides an estimate of SAX J1324.4−6200’s magnetic field strength of B ≈ 3 × 1016 G. Such a magnetic field would be stronger than the typical values inferred and measured from magnetars (see, e.g, Kaspi & Beloborodov 2017), but still below the maximal virial value of a NS of Bmax ≈ 1018 G (Mushtukov & Tsygankov 2022; Chandrasekhar & Fermi 1953). In light of this, we decided to also explore the non-accreting magnetar scenario. Recently, it has been proposed that the γ-ray binary LS 5039 contains a non-accreting magnetar (Yoneda et al. 2020). It was hypothesized that this source can tap into its magnetic energy to produce the observed emission. In particular, Yoneda et al. (2020) outlined the hypothesis that the interaction between the stellar wind of the companion star and the magnetar magnetosphere leads to magnetic reconnections that can release magnetic energy as radiation. Following the same line of reasoning as Yoneda et al. (2020), we find that if the compact object in SAX J1324.4−6200 is also a magnetar, the available energy budget from the magnetic energy would be the dissipation of the magnetic energy, 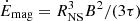 erg s−1 (see, e.g., Dall’Osso et al. 2012). Assuming a magnetic field strength of ∼1015 G (which is ten times smaller than the value obtained from the magneto dipole formula for pulsars but closer to the typical values encountered in magnetars) and a magnetic field decay timescale dominated by the so-called Hall term (τ ≈ 103 − 104 yr, see, e.g., Dall’Osso et al. 2012; Viganò et al. 2012, 2013; Turolla et al. 2015), the magnetic energy loss would be
erg s−1 (see, e.g., Dall’Osso et al. 2012). Assuming a magnetic field strength of ∼1015 G (which is ten times smaller than the value obtained from the magneto dipole formula for pulsars but closer to the typical values encountered in magnetars) and a magnetic field decay timescale dominated by the so-called Hall term (τ ≈ 103 − 104 yr, see, e.g., Dall’Osso et al. 2012; Viganò et al. 2012, 2013; Turolla et al. 2015), the magnetic energy loss would be 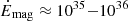 erg s−1. This
erg s−1. This 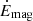 value is promisingly high in the case of SAX J1324.4−6200. However, the relatively low τ adopted here does not guarantee a magnetar-scale field and a magnetic energy actively dissipated in a magnetar with an age of ∼105 yr (see, e.g., Dubus 2013). This age corresponds to the most plausible evolutionary stage of a young binary system with a pulsar and a Be star. The presence of magnetars with these properties in γ-ray binaries and high-mass X-ray binaries is currently a matter of intense debate (see, e.g., Bozzo et al. 2008; Xu et al. 2022; Yoneda et al. 2020; Torres et al. 2012; Popov 2023, and references therein). In light of this, if we assume τ ∼ 105 yr, we obtain
value is promisingly high in the case of SAX J1324.4−6200. However, the relatively low τ adopted here does not guarantee a magnetar-scale field and a magnetic energy actively dissipated in a magnetar with an age of ∼105 yr (see, e.g., Dubus 2013). This age corresponds to the most plausible evolutionary stage of a young binary system with a pulsar and a Be star. The presence of magnetars with these properties in γ-ray binaries and high-mass X-ray binaries is currently a matter of intense debate (see, e.g., Bozzo et al. 2008; Xu et al. 2022; Yoneda et al. 2020; Torres et al. 2012; Popov 2023, and references therein). In light of this, if we assume τ ∼ 105 yr, we obtain 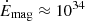 erg s−1, which is still large enough to power the radiation output of SAX J1324.4−6200.
erg s−1, which is still large enough to power the radiation output of SAX J1324.4−6200.
4.3. Accretion scenario
4.3.1. Accretion torque
We consider the case in which the X-ray luminosity is caused by the accretion of matter and the long-term spin-down is due to a torque generated by the exchange of angular momentum between the pulsar and the accreting matter. To assess quantitatively whether Lx, P, and Ṗ are compatible with this hypothesis, and which magnetic field strength is required, we compared our measurements with the predictions of three well-established models: Ghosh & Lamb (1979), Wang (1996), and Shakura et al. (2012). In the first two models, the accretion is mediated by a disc. In the Wang model, we assumed that the dissipation timescale of the toroidal component of the magnetic field is determined by the reconnection outside of the disc (see Wang 1995). For the inner disc radius, we adopted the prescription described in Bozzo et al. (2009). We set both η (a screening factor due to the currents induced on the surface of the accretion disc) and γmax (the maximum magnetic pitch angle), which appears in Eq. (19) in Bozzo et al. (2009), to equal 1. We note that these parameters are poorly known by the current theory, as is discussed in Bozzo et al. (2009). Moreover, both the Ghosh & Lamb (1979) and Wang (1995) prescriptions for the NS magnetospheric radius and accretion torques tend to display unphysical behaviors at low mass accretion rates, such that results in this regime should be taken with caution (Bozzo et al. 2009, 2018).
In the third accretion-torque model considered here, the long-term spin-down shown by SAX J1324.4−6200 could be the consequence of the quasi-spherical accretion of the stellar wind from the companion star onto the surface of the NS. Shakura et al. (2012, and references therein) pointed out that, if a pulsar in a binary system is wind-fed and the X-ray luminosity is moderate or low (Lx ≲ 1036 erg s−1), a hot quasi-static and convective shell forms around the magnetosphere of the NS. This shell can mediate the transfer of angular momentum, and the NS can spin up or down, depending on the difference between the angular velocity of the matter near the magnetospheric boundary and that of the magnetosphere itself. In contrast with the free-fall accretion regime, which produces a more erratic torque reversals (see, e.g., Bildsten et al. 1997; Malacaria et al. 2020, and references therein) the mechanism proposed by Shakura et al. (2012) can explain the predominance of a long-term spin-up or spin-down, although it can be interrupted by short episodic events of the opposite spin rate and other fluctuations (see, e.g., González-Galán et al. 2012). As is noted in Postnov et al. (2014), for pulsars that exhibit long-term spin-down (i.e., in non-equilibrium), it is possible, under some reasonable simplifications, to obtain a lower bound on their magnetic field strength from the spin-down rate, which can be expressed as
In the equation above, Πsd is a combination of dimensionless parameters of the theory: it varies from ∼4 to ∼10 (Postnov et al. 2015). Here, we assume that Πsd = 5 (due to the lack of information about the binary separation and properties of the stellar wind). Then, the magnetic dipole moment is expressed as μ30 = μ/(1030 G cm3), Ṁ16 = Ṁ/(1016 g s−1) is the mass accretion rate, and P100 is the spin period in units of 100 s.
The results are summarized in Fig. 9. The plot shows the X-ray luminosity on the x axis and the spin period derivative on the y axis. The black rectangle corresponds to the measurements of Ṗ and the X-ray luminosity, the latter depending on the distance of SAX J1324.4−6200. The curves intersecting the black rectangle were obtained using the Ghosh & Lamb (1979), Wang (1995), and Shakura et al. (2012) models, and represent the limiting solutions that can intersect the black rectangle. The magnetic fields of these solutions are B ≳ 1012 − 1013 G, which are typical of accreting pulsars in high-mass X-ray binaries. The Ṗ − Lx solutions obtained with the Ghosh & Lamb (1979) and Wang (1995) models for d = 15 kpc show steep slopes (see Fig. 9). This means that we would expect frequent torque reversals for small variations in the mass accretion rate. On the contrary, in Sect. 3.1 we have shown that Ṗ of SAX J1324.4−6200 is remarkably stable since its discovery; that is, for a time interval of ≥29 yr. Also, Lx (a proxy of the mass accretion rate) did not vary significantly: SAX J1324.4−6200 never showed an X-ray outburst or a flare (typical of most of Be/XRBs) in any observation. This observational evidence suggests that the mass accretion rate on the pulsar must be highly stable. We note the small flux variability between the NuSTAR+XRT and XMM-Newton observations (see Table 4). This could be due to a fluctuation in the mass accretion rate and, consequently, of the accretion torque rate, and might therefore also account for the NuSTAR spin period measurement that deviates from the long-term spin-down trend shown in Fig. 3. Another important point is that the overall properties of the X-ray spectrum of SAX J1324.4−6200 (a relatively hard X-ray spectrum, with a possible blackbody component with kTbb ≳ 1.1 keV, Sect. 3.2) are in agreement with the spectra observed in accreting high-mass X-ray binaries (see, e.g., Kretschmar et al. 2019).
 |
Fig. 8. Confidence contours at 68%, 90%, and 99% on the Γ − NH plane of the XRT+NuSTAR and XMM-Newton+NuSTAR fits (see Table 4). |
 |
Fig. 9. Ṗ − Lx functions from the (Ghosh & Lamb 1979, GL79, dashed lines) (Wang 1995, W95, dot-dash lines) and (Shakura et al. 2012, S12, dot lines) models corresponding to the minimum and maximum values of the magnetic dipole moment. These lines are the limits of the solutions obtained from these models that are in agreement with the observed spin period derivative of SAX J1324.4−6200 and its X-ray luminosity as a function of the distance (black rectangle). |
The pulsed fraction of SAX J1324.4−6200 reported in Table 3 is relatively high, in agreement with the typical pulsed fractions observed in other accreting X-ray pulsars with a high magnetic field, although it is remarkably stable with the energy, while in the other accreting systems it shows a general increase with the energy (see, e.g. Lutovinov & Tsygankov 2009; Ferrigno et al. 2023).
There exists another persistent Be/XRB that exhibits an uninterrupted long-term spin-down similar to SAX J1324.4−6200: CXOU J225355.1+624336. Its spin-down has a rate comparable to that of SAX J1324.4−6200 and it has been ongoing for at least 21 yr (La Palombara et al. 2021; Esposito et al. 2013). This similarity, together with the overall X-ray properties of SAX J1324.4−6200 emerging from our X-ray analysis, strengthens the hypothesis that SAX J1324.4−6200 belongs to the elusive class of persistent Be/XRBs.
4.3.2. γ-ray emission from an accreting pulsar
Only a few other accreting pulsars in Be/XRBs have a γ-ray counterpart candidate (for a list of XRBs with a γ-ray counterpart candidate, see e.g., Ducci et al. 2023). Different types of models have been proposed to explain the possible γ-ray emission from accreting pulsars. Here, we consider two of them. The first model, developed by Bednarek (2009a,b), introduced concepts that were further developed by Papitto et al. (2014; see also Torres et al. 2012; Papitto et al. 2012) to explain the γ-ray emission from the low-mass X-ray binary XSS J12270−4859. The model proposed by Bednarek (2009a,b) considers a binary system composed of an accreting and strongly magnetized NS and a companion massive star (OB type). Under certain conditions, the interaction between the NS magnetosphere and the dense wind from the donor star results in the creation of a magnetized and turbulent transition region around the pulsar. Within this region, electrons are accelerated to high energies, and subsequently produce γ-rays (up to few GeV) through synchrotron processes and inverse Compton scattering, in response to the X-ray radiation emitted from the NS surface. The maximum energy budget available to accelerate the electrons is limited by the energy that can be extracted by the matter interacting with the magnetosphere corotating with the NS. Bednarek (2009a) showed that the upper limit of the power available for the acceleration of electrons is
where B12 is the magnetic field strength at the polar cap of the NS, in units of 1012 G, Ṁ16 is the mass accretion rate, Ṁacc, in units of 1016 g s−1, and η is the fraction of the power that can be effectively converted to relativistic electrons and subsequently to γ-ray radiation. To calculate 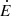 from Eq. (3), we derived the mass accretion rate from the formula Lx ≈ GMns Ṁacc/Rns, assuming Lx within the range ≈4.8 − 480 × 1033 erg s−1, Mns = 1.4 M⊙, and Rns = 12 km. Then, we adopted the corresponding limits for the magnetic field strength of the NS that we derived from the accretion torque models of Ghosh & Lamb (1979), Wang (1995), and Shakura et al. (2012): B ≈ 1012 − 9 × 1013 G. From Eq. (3), we obtain that the maximum power available for accelerating the electrons is
from Eq. (3), we derived the mass accretion rate from the formula Lx ≈ GMns Ṁacc/Rns, assuming Lx within the range ≈4.8 − 480 × 1033 erg s−1, Mns = 1.4 M⊙, and Rns = 12 km. Then, we adopted the corresponding limits for the magnetic field strength of the NS that we derived from the accretion torque models of Ghosh & Lamb (1979), Wang (1995), and Shakura et al. (2012): B ≈ 1012 − 9 × 1013 G. From Eq. (3), we obtain that the maximum power available for accelerating the electrons is 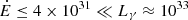 erg s−1.
erg s−1. 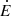 is further reduced if we consider the efficiency conversion factor, η ≈ 0.1 (Bednarek 2009a). Therefore, this mechanism cannot explain the observed γ-ray emission.
is further reduced if we consider the efficiency conversion factor, η ≈ 0.1 (Bednarek 2009a). Therefore, this mechanism cannot explain the observed γ-ray emission.
The second model we consider here was originally proposed by Cheng & Ruderman (1989; see also Bisnovatyi-Kogan et al. 1980) and subsequently improved by others (Cheng et al. 1991, 1992; Cheng & Ruderman 1991; Romero et al. 2001; Orellana et al. 2007; Ducci et al. 2023). The key concept of this model is that γ-ray photons are the result of cascades initiated by the decay of π0, which originate from protons accelerated in the magnetosphere of a pulsar fed by an accretion disc. Here, we consider the model version presented in Ducci et al. (2023) where the evolution of cascades inside and outside the accretion disc takes into account pair and photon production processes that involve interactions with nuclei, X-ray photons from the accretion disc, and the magnetic field. This model provides results above 10 GeV, so it cannot be directly compared with the Fermi/LAT detection reported by Harvey et al. (2022), which is in the 0.3 − 10 GeV energy range (see Fig. 10). Nevertheless, the model predictions can be compared with the Fermi/LAT upper limits at higher energies (10 − 300 GeV) reported in Harvey et al. (2022) and with the 5σ upper limit obtained from the High Energy Stereoscopic System (H.E.S.S) survey of the Galactic plane at energies > 1 TeV (H.E.S.S. Collaboration 2018). The H.E.S.S. upper limit can be obtained from the sensitivity map reported in H.E.S.S. Collaboration (2018) at the position corresponding to that of the γ-ray source detected by Harvey et al. (2022). Following the model in Ducci et al. (2023), we simulated a grid of γ-ray spectra expected for a source with the properties of SAX J1324.4−6200; in other words, with an X-ray luminosity in the range of Lx ≈ 5 − 500 × 1033 erg s−1, a magnetic field strength in the range of 1012 − 9 × 1013 G, and a spin period of 175 s. Among the possible solutions, we considered those for the “strong shielding” case. This is an approximation in which the X-ray photons produced by accretion at the stellar surface (including the accretion column) are strongly shielded by the accreting matter. In the case of “weak shielding,” the overall reduction of the potential drop over the region where the protons are accelerated would, in the case of SAX J1324.4−6200, lead to solutions with γ-ray emission much lower than in the case of strong shielding, and thus of much less interest, as we will see below. In general, all simulated spectra in the case of strong shielding give γ-ray fluxes well below the Fermi/LAT and H.E.S.S. upper limits (< 2 orders of magnitude). An extrapolation of the Harvey et al. (2022) detections to higher energies (i.e., above 10 GeV), or conversely an extrapolation of the simulated data to lower energies, shows that the observed emission is > 100 times brighter than that predicted by the model. To illustrate this result more clearly, we show in Fig. 10, as an example, a comparison between the observed data and the simulated spectrum obtained by assuming Lx = 5 × 1035 erg s−1 (and thus d = 15 kpc) and B = 4 × 1013 G. The simulated spectrum takes into account the apparent flux increase due to a beaming factor of bf = 0.03, which is also provided by the simulations. The other simulated spectra, not shown here, display an analogous low γ-ray emission. Therefore, although a direct comparison between observed and simulated data below 10 GeV is not possible, based on the constraints given by the upper limits above 10 GeV, and assuming that the observed (simulated) spectrum can be extrapolated smoothly at higher (lower) energies (i.e., without unphysical sharp jumps in fluxes greater than two orders of magnitude), it is reasonable to conclude that this mechanism cannot explain the intensity of the γ-ray emission reported in Harvey et al. (2022), either.
 |
Fig. 10. Comparison between observed and simulated spectra of SAX J1324.4−6200. Black circles: simulated spectral energy distribution expected from SAX J1324.4−6200, if it produces γ-ray emission with the mechanism presented in Ducci et al. (2023). The assumed X-ray luminosity, magnetic field strength, distance, and beaming factor, are reported in the legend of the figure. Blue squares: Fermi/LAT spectrum measured by Harvey et al. (2022, see their Fig. 3). Red diamond: upper limit obtained from the H.E.S.S. Galactic survey. |
4.4. Extragalactic active galactic nucleus scenario
In this section, we consider the hypothesis that the γ-ray source detected by Harvey et al. (2022) and positionally associated with SAX J1324.4−6200 could be an extragalactic AGN, observed through the Galactic plane. To test how likely this hypothesis is, we estimated the expected number of AGNs that Fermi/LAT could detect within a circle with a 95% radius of R95 = 0.1859°. We based our calculation on the number of AGNs reported in the Fourth LAT AGN Catalog (4LAC-DR3, Ajello et al. 2023)7 within ±5° of the Galactic plane. We call the density of the AGNs detected by Fermi/LAT within this area ρAGN. We considered only AGNs observed through the Galactic plane because we expect a lower density of these background sources than at higher Galactic latitudes, due to the effects of absorption. We assumed that AGNs are uniformly distributed and that the circle 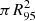 is small enough to neglect other effects (such as the curvature of the sky). Using the definition of the Poisson distribution, and given that the expected number of AGNs in the circle is
is small enough to neglect other effects (such as the curvature of the sky). Using the definition of the Poisson distribution, and given that the expected number of AGNs in the circle is 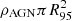 , the probability of having at least one AGN within
, the probability of having at least one AGN within 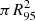 is
is 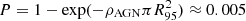 . Although this probability is very low, it shows that the possibility that the source detected by Harvey et al. (2022) is a background AGN cannot be discarded at a significance level of 0.5%. The 100 MeV−500 GeV flux of the γ-ray source detected by Harvey et al. (2022) is ≈2.98 × 10−6 MeV cm−2 s−1. This flux is well within the range of fluxes of AGNs reported in 4LAC-DR3 within ±5° of the Galactic plane, which is ≈6 × 10−7 − 8 × 10−5 MeV cm−2 s−1. If the γ-ray source detected by Harvey et al. (2022) were located at a distance corresponding to the average redshift of AGNs observed within ±5° of the Galactic plane (z ≈ 0.15), its luminosity would be approximately 3 × 1044 erg s−1 (100 MeV−100 GeV). This value is close to the average luminosity of the AGN sample selected for this calculation from the 4LAC-DR3 catalog, LAGN = 7 × 1044 erg s−1. The 100 MeV−100 GeV luminosities of our sample of AGNs spread over the range ∼1040 − 1049 erg s−1. The spectral index of the γ-ray source detected by Harvey et al. (2022) is also compatible with that expected from an AGN, as is indicated in the 4LAC-DR3 catalog. In conclusion, while the 0.5% probability of an extragalactic AGN observed through the Galactic plane coincidentally falling within the R95 radius of the γ-ray source detected by Harvey et al. (2022) is low, the extragalactic AGN scenario remains plausible.
. Although this probability is very low, it shows that the possibility that the source detected by Harvey et al. (2022) is a background AGN cannot be discarded at a significance level of 0.5%. The 100 MeV−500 GeV flux of the γ-ray source detected by Harvey et al. (2022) is ≈2.98 × 10−6 MeV cm−2 s−1. This flux is well within the range of fluxes of AGNs reported in 4LAC-DR3 within ±5° of the Galactic plane, which is ≈6 × 10−7 − 8 × 10−5 MeV cm−2 s−1. If the γ-ray source detected by Harvey et al. (2022) were located at a distance corresponding to the average redshift of AGNs observed within ±5° of the Galactic plane (z ≈ 0.15), its luminosity would be approximately 3 × 1044 erg s−1 (100 MeV−100 GeV). This value is close to the average luminosity of the AGN sample selected for this calculation from the 4LAC-DR3 catalog, LAGN = 7 × 1044 erg s−1. The 100 MeV−100 GeV luminosities of our sample of AGNs spread over the range ∼1040 − 1049 erg s−1. The spectral index of the γ-ray source detected by Harvey et al. (2022) is also compatible with that expected from an AGN, as is indicated in the 4LAC-DR3 catalog. In conclusion, while the 0.5% probability of an extragalactic AGN observed through the Galactic plane coincidentally falling within the R95 radius of the γ-ray source detected by Harvey et al. (2022) is low, the extragalactic AGN scenario remains plausible.
5. Conclusions
We have explored several scenarios to clarify the nature of the compact object in SAX J1324.4−6200 and the mechanism responsible for the γ-ray emission associated with this binary system. We have shown that the hypothesis that the emission of SAX J1324.4−6200 is due to colliding winds produced by the pulsar and the companion star (similar to what happens, for example, in the γ-ray binary PSR B1259-63; see, e.g., Tavani et al. 1994; Chernyakova et al. 2020) can be ruled out, as can the mechanisms of γ-ray emission production proposed by Bednarek (2009a,b) and Cheng & Ruderman (1989; in the updated form presented in Ducci et al. 2023). Our findings support the possibility that SAX J1324.4−6200 harbors a non-accreting magnetar and that its emission originates from magnetic energy loss, as is suggested for LS 5039 by Yoneda et al. (2020). However, we caution that the details of this mechanism are still too poorly understood to make any strong claims about it. Furthermore, we have shown that we cannot exclude the possibility, albeit small, that the observed γ-ray emission is produced by an extragalactic AGN, and that SAX J1324.4−6200 therefore hosts an accretion-powered pulsar in a persistent Be/XRB.
XSPEC version 12.13.1d (Arnaud 1996).
Acknowledgments
We thank the anonymous referee for constructive comments that helped improve the paper. L.D. acknowledges the kind hospitality of INAF – Osservatorio Astronomico di Cagliari, where part of this work was carried out, and the support by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG. We thank Norbert Schartel for approving the XMM-Newton DDT request and Lucia Ballo for scheduling the observation. We thank Brad Cenko for approving the Swift ToO request and the Swift team for scheduling the observation. Murriyang, the Parkes radio telescope, is part of the Australia Telescope National Facility (https://ror.org/05qajvd42) which is funded by the Australian Government for operation as a National Facility managed by CSIRO. We acknowledge the Wiradjuri people as the Traditional Owners of the Observatory site. This research has made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Space Science Data Center (SSDC, Italy) and the California Institute of Technology (Caltech, USA). This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. A.R. is supported by the Italian National Institute for Astrophysics (INAF) through an “IAF – Astrophysics Fellowship in Italy” fellowship (Codice Unico di Progetto: C59J21034720001; Project “MINERS”). A.R. also acknowledges continuing valuable support from the Max-Planck Society.
References
- Ajello, M., Baldini, L., Ballet, J., et al. 2023, VizieR Online Data Catalog: J/ApJS/263/24 [Google Scholar]
- Angelini, L., Church, M. J., Parmar, A. N., Balucinska-Church, M., & Mineo, T. 1998, A&A, 339, L41 [NASA ADS] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Avakyan, A., Neumann, M., Zainab, A., et al. 2023, A&A, 675, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bednarek, W. 2009a, A&A, 495, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bednarek, W. 2009b, MNRAS, 397, 1420 [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., Khlopov, M. Y., Chechetkin, V. M., & Eramzhyan, R. A. 1980, Soviet Ast., 24, 716 [NASA ADS] [Google Scholar]
- Bozzo, E., Falanga, M., & Stella, L. 2008, ApJ, 683, 1031 [Google Scholar]
- Bozzo, E., Stella, L., Vietri, M., & Ghosh, P. 2009, A&A, 493, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bozzo, E., Ascenzi, S., Ducci, L., et al. 2018, A&A, 617, A126 [NASA ADS] [EDP Sciences] [Google Scholar]
- Buccheri, R., Bennett, K., Bignami, G. F., et al. 1983, A&A, 128, 245 [NASA ADS] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 116 [Google Scholar]
- Cheng, K. S., & Ruderman, M. 1989, ApJ, 337, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., & Ruderman, M. 1991, ApJ, 373, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Yu, K. N., Cheung, T., & Lau, M. M. 1991, ApJ, 379, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Lau, M. M., Cheung, T., Leung, P. P., & Ding, K. Y. 1992, ApJ, 390, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Chernyakova, M., & Malyshev, D. 2020, Multifrequency Behaviour of High Energy Cosmic Sources - XIII. 3-8 June 2019. Palermo, Italy, 45 [Google Scholar]
- Chernyakova, M., Malyshev, D., Mc Keague, S., et al. 2020, MNRAS, 497, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
- Dall’Osso, S., Israel, G. L., Stella, L., Possenti, A., & Perozzi, E. 2003, ApJ, 599, 485 [CrossRef] [Google Scholar]
- Dall’Osso, S., Granot, J., & Piran, T. 2012, MNRAS, 422, 2878 [CrossRef] [Google Scholar]
- Doroshenko, V., Santangelo, A., Kreykenbohm, I., & Doroshenko, R. 2012, A&A, 540, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G. 2013, A&ARv, 21, 64 [Google Scholar]
- Dubus, G., Guillard, N., Petrucci, P.-O., & Martin, P. 2017, A&A, 608, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ducci, L., & Malacaria, C. 2022, in Modeling and Simulating X-ray Spectra, eds. C. Bambi, & A. Santangelo (Singapore: Springer Nature Singapore), 1 [Google Scholar]
- Ducci, L., Romano, P., Vercellone, S., & Santangelo, A. 2023, MNRAS, 525, 3923 [CrossRef] [Google Scholar]
- Esposito, P., Israel, G. L., Sidoli, L., et al. 2013, MNRAS, 433, 2028 [Google Scholar]
- Ferrigno, C., D’Aì, A., & Ambrosi, E. 2023, A&A, 677, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortin, F., García, F., Simaz Bunzel, A., & Chaty, S. 2023, A&A, 671, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortin, F., Kalsi, A., García, F., & Chaty, S. 2024, A&A, 684, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [Google Scholar]
- González-Galán, A., Kuulkers, E., Kretschmar, P., et al. 2012, A&A, 537, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- H.E.S.S. Collaboration (Abdalla, H., et al.) 2018, A&A, 612, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- Harvey, M., Rulten, C. B., & Chadwick, P. M. 2022, MNRAS, 512, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Manchester, R. N., Dunning, A., et al. 2020, PASA, 37, e012 [NASA ADS] [CrossRef] [Google Scholar]
- Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. M. 2017, ARA&A, 55, 261 [Google Scholar]
- Kaur, R., Wijnands, R., Patruno, A., et al. 2009, MNRAS, 394, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Kretschmar, P., Fürst, F., Sidoli, L., et al. 2019, New Astron. Rev., 86, 101546 [Google Scholar]
- La Palombara, N., & Mereghetti, S. 2007, A&A, 474, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Palombara, N., Sidoli, L., Esposito, P., Israel, G. L., & Rodríguez Castillo, G. A. 2021, A&A, 649, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, X. B., Church, M. J., Nagase, F., & Bałucińska-Church, M. 2002, MNRAS, 337, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., & Kramer, M. 2004, in Handbook of Pulsar Astronomy, (Cambridge, UK: Cambridge University Press), Cambridge Observing Handbooks for Research Astronomers, 4 [Google Scholar]
- Lutovinov, A. A., & Tsygankov, S. S. 2009, Astron. Lett., 35, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Forster, K., Grefenstette, B., Harrison, F. A., & Miyasaka, H. 2022, J. Astron. Telesc. Instrum. Syst., 8, 034003 [NASA ADS] [CrossRef] [Google Scholar]
- Malacaria, C., Jenke, P., Roberts, O. J., et al. 2020, ApJ, 896, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., & Taylor, J. H. 1977, Pulsars (San Francisco: W. H. Freeman, c1977) [Google Scholar]
- Mereghetti, S., Romano, P., & Sidoli, L. 2008, A&A, 483, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihara, T. 1995, Ph.D. Thesis, University of Tokyo, Japan [Google Scholar]
- Mushtukov, A., & Tsygankov, S. 2022, in Accreting Strongly Magnetized Neutron Stars: X-ray Pulsars, eds. C. Bambi, & A. Santangelo (Singapore: Springer Nature Singapore), 1 [Google Scholar]
- Neumann, M., Avakyan, A., Doroshenko, V., & Santangelo, A. 2023, A&A, 677, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orellana, M., Romero, G. E., Pellizza, L. J., & Vidrih, S. 2007, A&A, 465, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., Torres, D. F., & Rea, N. 2012, ApJ, 756, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Papitto, A., Torres, D. F., & Li, J. 2014, MNRAS, 438, 2105 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M., & Bordas, P. 2019, Rend. Lincei Sci. Fis. Nat., 30, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Pfahl, E., Rappaport, S., Podsiadlowski, P., & Spruit, H. 2002, ApJ, 574, 364 [Google Scholar]
- Popov, S. B. 2023, in Neutron Star Astrophysics at the Crossroads: Magnetars and the Multimessenger Revolution, eds. E. Troja, & M. G. Baring, 363, 61 [NASA ADS] [Google Scholar]
- Postnov, K. A., Shakura, N. I., Kochetkova, A. Y., & Hjalmarsdotter, L. 2014, in Physics at the Magnetospheric Boundary, Geneva, Switzerland, eds. E. Bozzo, P. Kretschmar, M. Audard, M. Falanga, & C. Ferrigno, EPJ Web Conf., 64, 02002 [NASA ADS] [Google Scholar]
- Postnov, K. A., Mironov, A. I., Lutovinov, A. A., et al. 2015, MNRAS, 446, 1013 [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [Google Scholar]
- Reig, P., & Roche, P. 1999, MNRAS, 306, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Kaufman Bernadó, M. M., Combi, J. A., & Torres, D. F. 2001, A&A, 376, 599 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N., Postnov, K., Kochetkova, A., & Hjalmarsdotter, L. 2012, MNRAS, 420, 216 [Google Scholar]
- Smith, D. A., Abdollahi, S., Ajello, M., et al. 2023, ApJ, 958, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Staubert, R., Trümper, J., Kendziorra, E., et al. 2019, A&A, 622, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [Google Scholar]
- Tanaka, Y. 1986, in IAU Colloq. 89: Radiation Hydrodynamics in Stars and Compact Objects, eds. D. Mihalas, & K.-H. A. Winkler, Lect. Notes Phys., 255, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., Arons, J., & Kaspi, V. M. 1994, ApJ, 433, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, D. F., Rea, N., Esposito, P., et al. 2012, ApJ, 744, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [CrossRef] [EDP Sciences] [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rep. Progr. Phys., 78, 116901 [Google Scholar]
- van Straten, W., & Bailes, M. 2011, PASA, 28, 1 [Google Scholar]
- van Straten, W., Demorest, P., & Oslowski, S. 2012, Astron. Res. Technol., 9, 237 [NASA ADS] [Google Scholar]
- Viganò, D., Pons, J. A., & Miralles, J. A. 2012, Comp. Phys. Commun., 183, 2042 [CrossRef] [Google Scholar]
- Viganò, D., Rea, N., Pons, J. A., et al. 2013, MNRAS, 434, 123 [CrossRef] [Google Scholar]
- Wang, Y. M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
- Wang, Y. M. 1996, ApJ, 465, L111 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Xu, K., Li, X.-D., Cui, Z., et al. 2022, Res. Astron. Astrophys., 22, 015005 [CrossRef] [Google Scholar]
- Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yoneda, H., Makishima, K., Enoto, T., et al. 2020, Phys. Rev. Lett., 125, 111103 [Google Scholar]
All Tables
Measurement of the spin period in the NuSTAR and XMM-Newton observations analyzed in this work.
Best-fit spectral parameters from the simultaneous fit of the Swift/XRT and NuSTAR (XRT+NuSTAR) and XMM-Newton data sets with an absorbed power law with a high energy cutoff, and constant renormalization factors.
Best-fit spectral parameters for the simultaneous fit of the Swift/XRT, NuSTAR, and XMM-Newton spectra with three different models.
All Figures
 |
Fig. 1. XMM-Newton pulse profiles of SAX J1324.4−6200 for three energy bands (ϕ = 0 at T0 = 60125.999592912 MJD). |
| In the text | |
 |
Fig. 2. NuSTAR pulse profiles of SAX J1324.4−6200 for three energy bands (ϕ = 0 at T0 = 601265.0 MJD). |
| In the text | |
 |
Fig. 3. Long-term evolution of the spin period of SAX J1324.4−6200 including the 1994 and 2000 ASCA observations, the 1997 BeppoSAX observation, the 2008 and 2023 XMM-Newton observations, the 2008 Swift observation, and the 2023 NuSTAR observation. The best-fitting linear model is shown (blue line). The bottom panel shows the residuals. |
| In the text | |
 |
Fig. 4. Left panel: XMM-Newton light curves (S = 0.2 − 5.2 keV and H = 5.2 − 12 keV) and HRs as a function of time (bintime = 527.586 s). Right panel: NuSTAR light curves (S = 3 − 9 keV and H = 9 − 60 keV) and HRs as a function of time (bintime = 527.4381 s). |
| In the text | |
 |
Fig. 5. Left panel: NuSTAR (black: module A; red: module B) and Swift/XRT (green) spectra of SAX J1324.4−6200, fit simultaneously with an absorbed power law with a high energy cutoff. Right panel: XMM-Newton (black: pn; red: MOS1; green: MOS2) spectra of SAX J1324.4−6200, fit simultaneously with an absorbed power law with a high energy cutoff (Ec and Ef frozen to the best fit values obtained from the XRT+NuSTAR fit). The lower panels show the residuals of the fit. |
| In the text | |
 |
Fig. 6. Same spectra as in Fig. 5, rebinned using setplot rebin in XSPEC, and thus for plotting purposes only, to better visualize the wave-like shape of the residuals. |
| In the text | |
 |
Fig. 7. XMM-Newton (black: pn; red: MOS1; green: MOS2), NuSTAR (blue: module A; cyan: module B), and Swift/XRT (orange) spectra of SAX J1324.4−6200 (rebinned using setplot rebin in XSPEC). Top panel: Spectra were fit simultaneously with an absorbed power law with a high energy cutoff and a Gaussian in absorption at ∼6.9 keV. Second panel: Residuals relative to the top panel. Third panel: Residuals of the fit of the spectra with an absorbed power law with a high energy cutoff and a blackbody. Bottom panel: Residuals of the fit of the spectra with an absorbed power law with a high energy cutoff. Table 5 lists the best fit parameters. |
| In the text | |
 |
Fig. 8. Confidence contours at 68%, 90%, and 99% on the Γ − NH plane of the XRT+NuSTAR and XMM-Newton+NuSTAR fits (see Table 4). |
| In the text | |
 |
Fig. 9. Ṗ − Lx functions from the (Ghosh & Lamb 1979, GL79, dashed lines) (Wang 1995, W95, dot-dash lines) and (Shakura et al. 2012, S12, dot lines) models corresponding to the minimum and maximum values of the magnetic dipole moment. These lines are the limits of the solutions obtained from these models that are in agreement with the observed spin period derivative of SAX J1324.4−6200 and its X-ray luminosity as a function of the distance (black rectangle). |
| In the text | |
 |
Fig. 10. Comparison between observed and simulated spectra of SAX J1324.4−6200. Black circles: simulated spectral energy distribution expected from SAX J1324.4−6200, if it produces γ-ray emission with the mechanism presented in Ducci et al. (2023). The assumed X-ray luminosity, magnetic field strength, distance, and beaming factor, are reported in the legend of the figure. Blue squares: Fermi/LAT spectrum measured by Harvey et al. (2022, see their Fig. 3). Red diamond: upper limit obtained from the H.E.S.S. Galactic survey. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



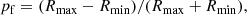
![$$ \begin{aligned} \dot{\omega }_{\rm sd} \approx -0.75 \times 10^{-12} \Pi _{\rm sd} \mu _{30}^{13/11} \dot{M}_{16}^{3/11} P_{100}^{-1} \ \ \mathrm{[rad\,s}^{-2}\mathrm{]}. \end{aligned} $$](/articles/aa/full_html/2024/05/aa49033-23/aa49033-23-eq59.gif)