| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202348899 | |
| Published online | 13 March 2024 | |
Which stars can form planets: Planetesimal formation at low metallicities
1
Department of Physics, Muni University,
PO Box 725,
Arua, Uganda
e-mail: g.andama@muni.ac.ug
2
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
3
Department of Physics, University College Cork,
Cork, Ireland
Received:
11
December
2023
Accepted:
26
January
2024
The diversity of exoplanets has been linked to the disc environment in which they form, where the host star metallicity and the formation pathways play a crucial role. In the context of the core accretion paradigm, the initial stages of planet formation require the growth of dust material from micrometre-sized to planetesimal-sized bodies before core accretion can kick in. Although numerous studies have been conducted on planetesimal formation, it is still poorly understood how this process takes place in low-metallicity stellar environments. In this work, we explore how planetesimals are formed in stellar environments with primarily low metallicities. We performed global 1D viscous disc evolution simulations, including the growth of dust particles and the evaporation and condensation of chemical species at ice lines. We followed the formation of planetesimals during disc evolution and tested different metallicities, disc sizes, and turbulent viscosity strengths. We find that at solar and sub-solar metallicities, there is a significant increase in the midplane dust-to-gas mass ratios at the ice lines, but this leads to planetesimal formation only at the water–ice line. In our simulations, [Fe/H] = −0.6 is the lower limit of metallicity for planetesimal formation where a few Earth masses of planetesimals can form. Our results further show that for such extreme disc environments, large discs are more conducive than small discs for forming large amounts of planetesimals at a fixed metallicity because the pebble flux can be maintained for a longer time, resulting in a longer and more efficient planetesimal formation phase. At lower metallicities, planetesimal formation is less supported in quiescent discs compared to turbulent discs, which produce larger amounts of planetesimals, because the pebble flux can be maintained for a longer time. The amount of planetesimals formed at sub-solar metallicities in our simulations places a limit on core sizes that could potentially result only in the formation of super-Earths.
Key words: planets and satellites: formation / protoplanetary disks
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
It is indisputable that the population of over 5500 confirmed exoplanets is diverse in terms of physical and chemical properties. Planets on close-in orbits have radii that range from that similar to the Earth to that similar to Jupiter, with a noticeable gap between the super-Earth and sub-Neptune populations (e.g. Fulton et al. 2017). In addition, recent observations have been making breakthroughs in characterising the atmospheric compositions of gas giants (e.g. Line et al. 2021; August et al. 2023; Bean et al. 2023; Pelletier et al. 2023). In order to understand the origin of the diversity, it is crucial to understand the environment in which the planets form and the building blocks that are available when the planets were growing. These factors are inherently associated with the host star and its accompanying protoplanetary disc.
Statistical analyses of carefully selected samples of planets and their host stars reveal that stellar metallicity (commonly parametrised as [Fe/H]), among other stellar properties, exerts a considerable influence on the occurrence rate of planets (e.g. Udry & Santos 2007; Petigura et al. 2018; Chen et al. 2022). Giant planets in particular tend to be found around stars with super-solar metallicities (e.g. Santos et al. 2004; Fischer & Valenti 2005; Johnson et al. 2010; Mortier et al. 2013; Petigura et al. 2018). This trend is also predicted by theoretical models of planet formation (e.g. Ida & Lin 2004; Mordasini et al. 2012; Bitsch et al. 2015b; Ndugu et al. 2018). Because stellar metallicity can be taken as a proxy for disc solid inventory (Hühn & Bitsch 2023), discs around stars with higher metallicities tend to have higher masses (Andrews et al. 2013) and metal contents. In the case of favourable disc properties such as large disc radii and high disc viscosities, solids in the disc can be sustained for long periods (Bitsch & Mah 2023), which can facilitate the formation of large planets (Lambrechts & Johansen 2014; Savvidou & Bitsch 2023).
The correlation with stellar metallicity, albeit weaker, is also present for sub-Neptunes and super-Earths (Wang & Fischer 2015; Petigura et al. 2018; see however Sousa et al. 2008; Buch-have et al. 2012). Interestingly, the ratio of super-Earths to sub-Neptunes increases with decreasing stellar metallicity (Chen et al. 2022), suggesting a correlation between stellar metallicity and the maximum size of the planetary cores that can form in the disc.
In general, stars with super-solar metallicities exhibit a greater diversity of planets than other stars. For example, stars with super-solar metallicities have a higher probability of hosting close-in planets (Mulders et al. 2016; Dong et al. 2018), high eccentricity planets (Buchhave et al. 2018; Mills et al. 2019), and multiple planets in the case of M-dwarf host stars (Rodríguez Martínez et al. 2023). This is perhaps unsurprising because the more solid material is available in the disc, the more possible formation pathways that a planetary core can follow there are, which will lead to a variety of outcomes (e.g. Lambrechts et al. 2019).
Planet occurrence rates around stars on the opposite end of the metallicity spectrum – the low-metallicity or iron-poor regime – have been relatively under-explored (Mortier et al. 2012; Boley et al. 2021). In models of planet formation, micrometre-sized dust first grows to pebbles via coagulation and condensation (Zsom et al. 2010; Ciesla 2010; Birnstiel et al. 2012; Ros & Johansen 2013) before overcoming a major growth barrier to become planetesimals. The formation of planetesimals is thought to proceed via the streaming instability (SI) mechanism (e.g. Youdin & Goodman 2005). Studies have shown that SI is effective in regions of the disc where the local dust-to-gas mass ratio and the pebble size are sufficiently large (e.g. Carrera et al. 2015; Yang et al. 2017; Li & Youdin 2021). Drążkowska & Alibert (2011) propose that the water-ice line is a prime location for the formation of the first generation planetesimals. This is due to the change in pebble size across the water-ice line; this alters the drift speed of the pebbles, creating a ‘traffic jam’ that eventually triggers the gravitational collapse of dust clumps that then form planetesimals. This location could also harbour a pressure perturbation driven by the difference in opacities caused by the difference in grain sizes interior and exterior to the water-ice line (Müller et al. 2021). The ring of planetesimals at the waterice line would then continue to grow and evolve via collisions or pebble accretion (Batygin & Morbidelli 2023; Woo et al. 2023).
Within the framework of this model, there should then be a lower limit to stellar metallicity, below which the pebble flux at the water-ice line is too low for planetesimal formation to kick in. Observations suggest that this limit is at −0.6 < [Fe/H] < −0.5 (Mortier et al. 2012), with the latest analysis suggesting it could be lower (between −0.7 and −0.6; Boley et al. 2021). Recent discoveries of planets around low-metallicity stars seem to be consistent with this metallicity limit (e.g. Hellier et al. 2014; Polanski et al. 2021; Brinkman et al. 2023; Dai et al. 2023).
Here we explore how planet formation works in a low-metallicity environment from a theoretical point of view. We do this by simulating the viscous evolution of the gas and the growth of dust particles in a protoplanetary disc with a 1D model that includes an additional effect, the evaporation and condensation of chemical species at ice lines (Schneider & Bitsch 2021). The evaporation and condensation effects generate a localised pileup of pebbles that can be converted into planetesimals under specific conditions (Drążkowska & Alibert 2017). We focus on understanding the minimum requirements that permit planetesimal formation in such extreme environments, how various disc properties influence the location where planetesimal formation takes place, the efficiency with which planetesimals are formed, and the total mass of the planetesimals produced.
We structure our paper as follows. In Sect. 2, we describe the disc and planetesimal formation models and the setup of the simulations. We present our results in Sect. 3 and then discuss and summarise our findings in Sect. 4.
2 Methods
2.1 Disc evolution and dust growth
Our work uses the chemcomp code presented in Schneider & Bitsch (2022). This 1D code computes the gas surface density by solving the viscous evolution equation (Lynden-Bell & Pringle 1974) and uses the alpha-viscosity Article number, page 2 of 15 prescription (Shakura & Sunyaev 1973). The disc model used in this work is one with a smooth surface density profile without any pressure perturbations. The disc’s kinematic viscosity is expressed as
where αt describes the strength of turbulence in the disc, cs is the isothermal sound speed and ΩK is the Keplerian orbital speed.
The temperature of the disc is contributed by two physical processes: viscous accretion (which operates in the inner disc) and stellar irradiation (which operates at larger orbital distances). The heat from viscous accretion depends on the disc's turbulent viscosity (αt) as well as the initial dust-to-gas ratio. The heat from stellar irradiation, on the other hand, depends only on the stellar luminosity, which is a fixed value in this work. Thus, a disc with a low dust-to-gas ratio will have a lower temperature in its inner region compared to a disc with high dust-to-gas ratio. For simplicity, the disc’s temperature profile in the code does not evolve in time.
Dust grains in the disc start out as sub-micrometre-sized grains that then grow via coagulation into larger size grains called pebbles. The size of the pebbles is limited by radial drift (grains above the drift limit drift quickly towards the central star and are lost) and fragmentation (grains that collide with a relative velocity greater than the fragmentation limit are broken up into smaller fragments; Birnstiel et al. 2012). Following results from laboratory experiments (Gundlach & Blum 2015), we assumed a fragmentation velocity of uf = 10 m s−1 for icy grains beyond the water-ice line and uf = 1 m s−1 for silicate grains closer in. The transition of fragmentation velocities results in different drift speeds of the grains at the water-ice line, leading to a ‘traffic jam’ (a region with a high local dust-to-gas ratio) just inside the water-ice line, which could promote the formation of planetesimals (Drążkowska & Alibert 2017).
The size and properties of dust grains in protoplanetary discs is a topic of intense research. Recent results from laboratory experiments (Musiolik & Wurm 2019) and simulations (Jiang et al. 2024) suggest that icy dust grains may actually be fragile and thus fragment at lower velocities. We show the outcome of the scenario when the dust grains have fragmentation velocity of 1 m s−1 in Appendix A.
A chemical model is also introduced to compute the composition of the dust grains. We show in Appendix B the elements and molecules we included in our simulations and their respective abundances in the disc. As the pebbles drift inwards to the central star, they cross the ice lines of the different molecules in the disc and release the vapour of the corresponding molecules to the gas (Schneider & Bitsch 2021). Some of the vapour can diffuse outwards and recondense to make new pebbles. This effect results in a locally enhanced pebble surface density (and dust-to-gas ratio) at the location of the ice lines.
2.2 Planetesimal formation
We incorporated the planetesimal formation prescription of Drążkowska & Alibert (2011), in which planetesimals form in regions of the disc where the pebble Stokes number and dust-togas ratio in the midplane exceed 10−2 and 1, respectively. Pebbles are then converted to planetesimals at a rate of
where ζ is the efficiency and ∑d is the dust surface density. We followed Drążkowska & Alibert (2011) and used ζ = 10−3.
We modified the condition for the Stokes number according to recent results on the SI (Li & Youdin 2021). In our model, planetesimals form when the following conditions are fulfilled: (i) the pebbles have Stokes number St > 10−3 and (ii) the midplane dust-to-gas ratio s = ρd/ρg ≥ 1.
The Stokes number of the pebbles is computed dynamically in the code using
where a is the pebble radius, ρ is the pebble density and ∑g is the gas surface density. As the code computes the vertically integrated dust-to-gas ratio, we recover the midplane value using
where Hd is the dust scale height, Hg is the gas scale height and αz describes the strength of vertical mixing. We note that Drążkowska & Alibert (2011) did not make the distinction between αt and αz. In our simulations, we find that planetesimals form when αz = 10−4, in agreement with the results of Drążkowska & Alibert (2011). However, we also tested the influence of vertical mixing in Appendix D.
2.3 Simulation setup
In the first set of simulations, we studied the conditions for planetesimal formation. We used a fixed mass for the central star, M* = 1 M⊙, and varied the disc mass, the disc characteristic radius, the strength of viscous turbulence, and the stellar metallicity. The initial dust-to-gas ratio, DTG, in the disc depends on the stellar abundance of all the elements included in the model. We computed this quantity using
where X/H is the initial abundance of element X in the disc (see Appendix B), µX is the atomic mass of element X, and [X/H] is the stellar abundance of element X as a function of [Fe/H] (Bitsch & Battistini 2020). For reference, we obtain DTG = 0.016 for [Fe/H] = 0.
In the second set of simulations, we explored the lower limit of DTG when planetesimal formation ceases. We fixed the disc mass and disc radius to Mdisc = 0.1 M⊙ and rc = 100 au, respectively, and varied αt and DTG. All simulations in both setups were run for 3 Myr with a time step of 10 yr. Tables 1 and 2 summarise the parameter spaces we explored. In the numerical setup, the inner and outer boundaries of the radial grid are set to 0.1 au and 1000 au, respectively, which allows all materials to leave our computational domain.
3 Results
3.1 Planetesimal formation at ice lines in quiescent discs
In Fig. 1, we show our results for planetesimal formation in quiescent disc with turbulent viscosity of αt = 10−4 at solar and sub-solar disc metallicities. In the top row, we show the evolution of the pebble and planetesimal surface densities at 0.1 Myr, 0.5 Myr, and 1 Myr. Here, the lines for the planetesimal surface density at different times fall on top of each other because our planetesimal formation takes place within a narrow annulus within the ice line. The total mass evolution of the planetesimals with time is provided in Sect. 3.4. In the bottom row, we show the connection between Stokes number and the midplane dust-to-gas ratio that set the conditions for planetesimal formation in our simulations.
As shown in the top panel of Fig. 1, planetesimal formation is prominent at the water-ice line compared to the ice lines of the other chemical species. This can be explained by the interplay between the pebble Stokes number and the local dust-to-gas ratio shown in the bottom panels of Fig. 1. Pebbles grow large in the less turbulent disc and possess drift limited sizes, which increase from outside to inside disc regions with a corresponding increase in the Stokes numbers. These large pebbles drift rapidly to the water-ice line region where they sublimate, releasing silicate grains. The released silicate grains undergo a transition in fragmentation velocities where they fragment at a lower velocity of 1 m s−1 in the disc regions interior to the water-ice line, producing smaller size pebbles with corresponding low Stokes number, as shown in the bottom panel of Fig. 1. Consequently, these dust grains are more coupled to the gas and drift at reduced velocities compared to the large pebbles in the disc regions exterior to the water-ice line. At the same time, the water vapour diffuses outwards from the disc region interior to the ice line and re-condenses to make new pebbles at the ice line. The repetition of this process eventually leads to a traffic jam within the water-ice line region (see also Pinilla et al. 2016; Drążkowska & Alibert 2017). The traffic jam effect causes a pileup of pebbles that leads to increased midplane dust-to-gas ratios, as shown in the bottom panel of Fig. 1. In addition, due to the high Stokes numbers, pebbles decouple from the gas, which allows them to settle and further boosts the midplane dust-to-gas ratio. However, in our simulations the condition to form planetesimals is fulfilled within the water-ice line region, where no planetesimals form in the other parts, as shown in the top panel of Fig. 1.
Here, planetesimals are formed at the water-ice line because it is a sweet spot where we can have new pebbles formed by recondensation of water vapour, but at the same time the Stokes numbers are still high enough to enable planetesimal formation.
At the carbon sublimation line, pebbles also pile up because of the re-condensation of carbon grains as carbon vapour diffuses outwards from the inside parts of the disc interior to the carbon sublimation line. Here, the dust pileup is stronger because the grains are small and do not drift so fast. This leads to high pebble surface densities and hence high dust-to-gas ratios at the carbon sublimation line, as shown in the bottom panel of Fig. 1. However, because of the low Stokes numbers in this region, the pebbles are more coupled to the gas and are less settled, which impedes planetesimal formation at the carbon sublimation line.
For the ice lines in the outer parts of the disc, the Stokes numbers are high but the dust-to-gas ratios are low, which makes it difficult for planetesimal formation to take place. This is because in these regions, the weak accumulation of pebbles at ice lines of the different chemical elements does not sufficiently enhance the dust-to-gas ratio to values suitable for planetesimal formation.
We attribute the weak accumulation of pebbles at these ice lines to the fact that, in our simulations, there is no fragmentation velocity difference at these ice lines that actually causes the traffic jam effect seen at the water-ice line. However, it needs to be tested if a fragmentation velocity transition could trigger planetesimal formation, especially at the CO2 and CO ice lines, at solar and sub-solar metallicities. While the change in fragmentation velocity at the water-ice line is motivated by experiments, it is difficult to perform the similar laboratory experiments for CO2 and CO ice. However, numerical simulations seem to suggest that enhanced grain growth might not take place just outside the CO ice line (Stammler et al. 2017).
Although planetesimal formation appears to be difficult at the evaporation fronts other than the water-ice line at solar metallicities, we show in Appendix C the possibility that planetesimal formation can take place at those ice lines in stellar environments with super-solar metallicities. This is because at the super-solar metallicities, significant quantities of frozen volatile species evaporate at the ice lines. Hence, larger amounts of vapour diffuse out compared to solar and sub-solar metallicities, which then re-condense to form new pebbles as explained before. In addition, at super-solar metallicities, there is an abundance of solid material. This results in significant dust-to-gas ratio enhancements, which in turn promotes planetesimal formation (e.g. Li & Youdin 2021).
In the less turbulent discs, reducing the disc metallicity to sub-solar values results in reduced planetesimal formation at the water-ice line, as shown in the middle and the right panels of Fig. 1. This is because, the lower the disc metallicity, the lower the amount of solid materials in the disc and the lower the dust-to-gas ratios. In addition, as already discussed above, dust grains drift faster in less turbulent discs (due to their larger size), which leads to faster depletion of solids; hence, small amounts of solids accumulate and transform into planetesimals at the water-ice line.
Parameter space explored in the first set of simulations.
Parameter space explored in the second set of simulations.
 |
Fig. 1 Planetesimal formation in a quiescent disc. Top: evolution of pebble and planetesimal surface densities for a nominal turbulent viscosity of αt = 10−4, a disc size of rc = 100 au, and different values of disc metallicity. Bottom: evolution of the Stokes numbers and the corresponding midplane dust-to-gas ratios. |
3.2 Planetesimal formation at ice lines in turbulent discs
Figure 2 shows how planetesimal formation takes place in a turbulent disc environment (using αt = 10−3). Again, here grain sizes play a key role for planetesimal formation. For example, in the bottom panel of Fig. 2, the grain sizes in the outer disc regions are in the drift limited regime. However, in the inner disc regions their sizes are limited by fragmentation levels. Hence, pebbles in the drift limited regime migrate faster than the pebbles in the fragmentation limit (indicated by the radial drop in Stokes number interior to 10–30 au), which drift more slowly due to their smaller size. Here, the transition between drift and fragmentation limits shifts with time from the outer to the inner disc regions, as shown in the bottom panel of Fig. 2. The more slowly drifting pebbles cause a traffic jam in the region interior to the point of transition between drift and fragmentation limits takes place. This results in accumulation of pebbles and hence a more enhanced dust-to-gas ratio at the CO2 line compared to the less turbulent disc as shown in the bottom panel of Fig. 2. However, both the Stokes number and the midplane dust-to-gas ratio at the CO2 line are below the thresholds that we set for planetesimal formation in our simulations.
In contrast to the weak turbulent viscosity, increasing the turbulence strength to αt = 10−3 promotes planetesimal formation for the case of the sub-solar metallicities as shown in Fig. 2. This is possibly because the high disc turbulence causes the fragmentation of pebbles to smaller sizes, which drift at reduced speeds and hence linger in the disc for longer periods of time compared to quiescent disc (see also Bitsch & Mah 2023). On the other hand, the onset of the dust pileup at the ice line could also reduce the radial drift velocities of the dust grains (Drążkowska et al. 2016). The longer radial drift times give a window of opportunity for dust grains to concentrate at the water-ice line, which can later form planetesimals once the planetesimal formation conditions are fulfilled. Here, we can maintain a high enough pebble flux for a longer time, which in turn allows the formation of planetesimals for a longer time, resulting in a larger fraction of formed planetesimals.
Furthermore, for the case of high turbulence strength of αt = 10−3, pebbles no longer accumulate at the carbon evaporation line, as shown in Fig. 2. This is because the high turbulence levels coupled with low fragmentation velocity in the inner disc regions converts pebbles to smaller dust materials, which have very small Stokes numbers as shown in the bottom panel of Fig. 2. These small size dust grain are more coupled to the gas and follow gas streamlines. These well-coupled dust grains drift more slowly but the high gas viscosity transports the carbon vapour away more efficiently onto the star. This impedes recondensation of the carbon vapour to make new pebbles at the carbon sublimation line, leading to lower midplane dust-to-gas ratios compared to the less turbulent disc.
 |
Fig. 2 Planetesimal formation in a turbulent disc. Top: evolution of pebble and planetesimal surface densities for a nominal turbulent viscosity of αt = 10−3, a disc size of rc = 100 au, and different values of disc metallicity. Bottom: evolution of the Stokes numbers and the corresponding midplane dust-to-gas ratios. |
3.3 The role of volatiles
The volatiles play an important role in regulating the dust-togas ratios and Stokes numbers as shown in the bottom panels of Figs. 1 and 2. For example, between the CO and water ice sublimation lines, the dust-to-gas ratios and the Stokes numbers gradually decrease and increase, respectively. At the sublimation fronts, there is a spike in both the dust-to-gas ratios and the Stokes number. In our simulations, particles grow to larger sizes as they migrate to the inner disc regions, where the Stokes numbers also increase. Particles grow even larger at the sublimation lines as a result of the drift limited approximation, where the particle sizes increase with dust surface density (Birnstiel et al. 2015). The large pebbles have correspondingly high Stokes numbers, which leads to a more efficient settling of pebbles. This in turn leads to an increase in the midplane dust-to-gas ratios. However, the increased Stokes number also allows pebbles to drift faster to the next ice line, which leads to a drop in the dust-to-gas ratios between the ice lines. Here, pebbles instead accumulate temporarily, especially at ice lines for the volatile pebble species.
The accumulation of pebbles is more pronounced within the water-ice line because there is a change in fragmentation velocities of the grains interior and exterior to the ice line region. As mentioned before, the larger ice rich pebbles drift fast, increasing the water vapour in the inner disc interior to the water-ice line. In the interior disc regions, the released dry silicates remain small in size because they fragment at a low velocity of 1 m s−1. The small dust grains have corresponding low Stokes numbers interior to the water-ice line. The small dust grains then become more coupled to the gas and the outward diffusion carries them outwards, where they can grow back to larger sizes, leading to an accumulation of pebbles within the ice line region. This back and forth grain transport process is enhanced by increasingly rapid inward drift of pebbles in between the ice lines. The rapid transition of the drift velocity at the waterice line leads to a traffic jam, a high accumulation of pebbles, and increased dust-to-gas ratios, which promotes planetesimal formation (Drążkowska & Alibert 2017).
A change in fragmentation velocity at different ice lines of the volatile pebble species could result in dust surface density enhancements (Pinilla et al. 2017), leading to the possibility of planetesimal formation at those ice lines. In addition, studies show that sintering of aggregates consisting of multiple species of volatile ices could result in dust pileup in multiple locations close to the ice lines (Okuzumi et al. 2016). Consequently, this could also support planetesimal formation at the different ice lines under favourable conditions. However, the effect of both sintering and changes in the fragmentation velocity at multiple ice line locations is beyond the scope of this paper and will be treated in a future work.
3.4 Time evolution of planetesimal mass at the water-ice line
To put planetesimal formation at the water-ice line in perspective in terms of the total mass of pebbles converted into planetesimals, we explored four parameters that might constrain planetesimal formation in our disc model. We then discuss what time planetesimal formation kick-starts during disc evolution.
3.4.1 Dependence on metallicity
We explored planetesimal formation for different values of disc metallicity ranging from solar to sub-solar values to infer the minimum requirement of disc metallicity for planetesimal formation. Our results are shown in Fig. 3, where the general trend is that the amount of planetesimals in Earth masses formed decreases as the disc metallicity decreases. This is expected because the disc metallicity, which is used as a proxy for calculating the DTG, determines the availability of solid materials in the disc. This means that the higher the metallicity, the higher the amount of solids available for potential formation of planetesimals.
The top panel of Fig. 3 shows how planetesimal formation takes place in a quiescent disc at different metallicity values. Here, planetesimals form within 0.05 Myr of disc evolution, where no more conversion of pebbles takes place shown by the flat curves. Here, a few Earth masses of up to 35 ME of planetesimals form for the case of [Fe/H] = 0. However, the amount of planetesimals formed drops to very low values when we reduce the metallicity to sub-solar values. For example, for the case of [Fe/H] = −0.4, very negligible amount of planetesimals is formed and only a fraction of Earth masses of planetesimal form for the case of [Fe/H] = −0.2. This suggests that a quiescent disc is not a favourable environment for formation of planetesimals at low disc metallicities. Probably, this is because, at low viscosity, the grains interior to the ice line are still large enough that they slightly decouple from the gas and drift inwards fast enough to prevent the traffic jam effect. In contrast, at higher viscosity, the traffic jam effect persists, because the pebbles are smaller and thus drift inwards more slowly, as explained earlier (see also Bitsch & Mah 2023).
In the turbulent disc with αt = 10−3, as shown in the bottom panel of Fig. 3, considerable Earth masses of planetesimals are formed even at low disc metallicities, where at least 40 ME planetesimals form for the case of [Fe/H] = −0.4. This is several orders of magnitude larger compared to a quiescent disc with a metallicity of [Fe/H] = −0.4. This demonstrates that moderately turbulent disc environments are beneficial for planetesimal formation because of their grain retention capabilities as earlier explained. However, in highly turbulent discs, for example with αt = 10−2, grains might become too small in the fragmentation limit and drift too slowly that planetesimal formation becomes difficult (e.g. Drążkowska & Alibert 2017). Nevertheless, for planetesimal formation to take place at the water-ice line in stellar environments with sub-solar metallicities, the surrounding discs must be turbulent enough in order to produce relatively small size pebbles and scale down the loss of pebbles via radial drift on short dynamical timescales. However, at low viscosities, the presence of pressure bumps could also slow down grain migration (Pinilla et al. 2012; Andama et al. 2022), which could allow more planetesimals to form at the ice line (e.g. Stammler et al. 2019).
Our numerical code lacks scaling for metallicity values below [Fe/H] = −0.4 that self-consistently computes DTGs for dust evolution and the accurate chemical composition. This is because the stellar abundances from GALAH surveys (Buder et al. 2018) on which the dust-to-gas scaling in the code is based (Bitsch & Battistini 2020; Schneider & Bitsch 2021) span [Fe/H] values from −0.4 to +0.4. However, we extrapolated the DTGs to the lowest value of [Fe/H] = −0.7. Therefore, in order to infer the lowest limit placed on metallicity for planetesimal formation, we performed simulations directly with lower values of DTG below the value for [Fe/H] = −0.4, ranging from 0.005 to 0.008, corresponding to [Fe/H] = −0.7 and [Fe/H] = −0.4, respectively. The results, shown in Fig. 4, suggest that a DTG of about 0.006 (corresponding to [Fe/H] = −0.6) is the lower limit required for planetesimal formation to take place. In our simulations, for this lower limit of DTG, only a Moon mass amount of planetesimals can form in a quiescent disc, but a few Earth masses of planetesimals can form for the case of a turbulent disc. Here, as shown in Fig. 4, planetesimal formation starts relatively late because the amount of disc material is small, which takes time to accumulate at the ice lines in contrast to discs with higher metallicities. Our results on the limits placed by the availability of dust materials for planetesimal formation to take place are in line with the results of the recent SI simulations (Li & Youdin 2021).
 |
Fig. 3 Metallicity dependence of planetesimal formation at the waterice line. |
 |
Fig. 4 Lower limit of the DTG for planetesimal formation at the water-ice line in a disc with rc = 100 au. |
3.4.2 Dependence on disc mass
In Fig. 5, we show how planetesimal formation at water-ice line scales with the initial disc mass and turbulent viscosity, where the top and bottom panels show quiescent and turbulent discs, respectively. To test the lower limit of disc mass that can support planetesimal formation at the water-ice line, we performed simulations with lower disc masses Mdisc = 0.05 M⊙ and Mdisc = 0.01 M⊙, with the corresponding initial dust masses of 250 ME and 50 ME, respectively.
As shown in Fig. 5, relatively significant amounts of planetesimals are formed even in the least massive disc in our simulations, where we obtained at least 25 ME in planetesimals for the case of Mdisc = 0.01 M⊙ and αt = 10−3. Here, nearly half of the pebbles are lost to the central star via radial drift. This raises the question of whether pebble accretion can support planet formation in stellar environments with such low disc masses, which is in fact difficult, as shown in Savvidou & Bitsch (2023). However, the above picture may not necessarily limit pebble accretion. For example, substantial amounts of planetesimals are formed before 0.1 Myr, where the formation process stops at around 0.2 Myr. These planetesimals could coalesce into a planetary embryo that could accrete any subsequent pebbles that accumulate at the ice line. Moreover, the planetary embryo at the water-ice line could accrete the accumulated pebbles very efficiently before they are converted into planetesimals (Morbidelli 2020; Izidoro et al. 2021; Andama et al. 2022) or accrete other planetesimals within this region (Chambers 2023; Batygin & Morbidelli 2023).
In summary, within the limits of disc masses explored in this study, the existence of a water-ice line within a disc with a transition in fragmentation velocity at the ice line is sufficient to promote planetesimal and hence planet formation. This means that even stellar environments with low disc masses are still conducive for planet formation, provided they are sufficiently turbulent with large radial extent to minimise rapid loss of pebbles.
 |
Fig. 5 Disc mass dependence of planetesimal formation at the waterice line in a disc environment with [Fe/H] = 0. The vertical dotted lines in the bottom panel show the points at which the curves start to level off, where planetesimals stop forming. |
3.4.3 Dependence on disc size
We ran another set of simulations to test the dependence of planetesimal formation on the disc size, and our results are shown in Fig. 6. In the quiescent discs, shown in the top panel of Fig. 6, the planetesimal formation times at the water-ice line are insensitive to the disc size, where roughly the same amount of planetesimals take about the same time to form. On the other hand, in the bottom panel of Fig. 6 for the turbulent disc, planetesimal formation takes longer time in a large disc compared to a small disc. These observed trends can best be explained by how the disc size affects pebble flux during the course of disc evolution. In large discs, we can maintain pebble flux for a longer time than in small discs, which is, however, smaller, explaining the initially lower planetesimal formation efficiency at the water-ice line compared to smaller discs, where the pebble flux is initially higher. However, for a low viscosity of αt = 10−4, we lose pebbles faster, almost on similar dynamical timescales, in both large and small discs with small difference in the amount of formed planetesimals.
In turbulent discs with αt = 10−3, the completion times of planetesimal formation at the water-ice line depend on the radial extent of the disc, which increases with increasing rc. For example, in our simulations, it takes about 0.2 Myr and 0.4 Myr for planetesimal formation at the water-ice line to complete in a small disc with rc = 60 au and a large disc with rc = 200 au, respectively. The reason for this is that, at high viscosity, pebbles take longer time to drift from the outer disc regions and accumulate at the water-ice line. Consequently, in larger discs, pebbles drift over longer distances compared to the smaller size discs, where the drift times are shorter. In addition, it takes longer for the pebble flux to decay in larger discs, because the pebbles still need to form in the outer regions before they drift inwards (Lambrechts & Johansen 2014; Bitsch et al. 2018; Bitsch & Mah 2023).
From the bottom panel of Fig. 6, we see that about 250 ME of planetesimals forms at the water-ice line in the large disc with rc = 200 au; in the small disc with rc = 60 au, in contrast, roughly 190 ME of planetesimals forms. This is because, as mentioned above, the large disc retains pebbles for longer periods as more pebbles are produced from the disc’s outskirts with the outward shift in the pebble production line (Lambrechts & Johansen 2014). In contrast, in small discs, pebbles drain faster, and hence planetesimal formation stops early on, resulting in small amounts of planetesimals. In our simulations, planetesimal formation stops before 1 Myr, inconsistent with the Solar System, where planetesimal formation is expected to take place at all stages, as inferred from the estimates of chondrite ages (Amelin et al. 2002; Kleine et al. 2009; Connelly et al. 2012; Kruijer et al. 2014, 2017; Onyett et al. 2023). However, this can be attributed to the disc structure used in our simulations that do not feature disc substructures due perturbations in the disc structure. As mentioned earlier, perturbations in the gas density could accumulate pebbles and aid planetesimal formation at later stages of disc evolution (e.g. Izidoro et al. 2021).
 |
Fig. 6 Disc size dependence of planetesimal formation at the water-ice line. The vertical dotted lines have the same meaning as in Fig. 5. |
 |
Fig. 7 Disc turbulence dependence of planetesimal formation at the water-ice line in a disc with rc = 100 au and [Fe/H] = 0. Top: time evolution of the total solid mass without planetesimal formation taking place in the disc. Bottom: time evolution of the dust and pebble mass, including planetesimal formation in the disc. |
3.4.4 Dependence on disc turbulence
The main role played by the turbulent viscosity has been discussed in the previous sections. Here, we further show how it impacts planetesimal formation in terms of the total dust mass lost via radial drift of pebbles for nominal disc size of rc = 100 au and disc metallicity of [Fe/H] = 0. As shown in the bottom panel of Fig. 7, about 35 ME of the initial dust mass of about 400 ME is converted into planetesimals at the water-ice line in a quiescent disc with αt = 10−4. In contrast, for the case of a turbulent disc with αt = 10−3, about 200 ME of planetesimals are formed, representing 50% conversion rate of the initial total solid mass. As shown in the top panel of Fig. 7, after 3 Myr of disc evolution about 200 ME of dust is still present in the disc with αt = 10−3. However, for the disc with αt = 10−4, about 30 ME of dust material remains. As discussed before, dust grains are depleted more rapidly in quiescent discs compared to the turbulent discs, which have better dust retention, which explains the disc mass evolution trends in Fig. 7.
In addition, disc turbulence may impact planetesimal formation at the ice lines by influencing the diffusive processes within the ice line regions. For example, high turbulence levels could transport material outwards to the ice line regions faster (compared to low turbulence levels) where dust grains can grow to centimetre size pebbles (Ros & Johansen 2013; Ros et al. 2019). However, in our simulations, we did not test to what extent this process would affect planetesimal formation at the ice lines.
3.5 Comparison with other studies
In our simulation, we record accumulation of pebbles within a very narrow annulus around the ice line, in contrast to Drążkowska & Alibert (2011). This is because we did not include backreaction of the solids on the gas that would cause traffic jam effect in broader disc regions. In addition, in the Drążkowska & Alibert (2011) model, both the changes in fragmentation velocity at the ice line and the dust backreaction on the gas work in tandem, further amplifying the traffic jam effect. However, in our simulations, the traffic jam is solely driven by the changes in fragmentation levels of the pebbles at the ice line. Without backreaction, we were able to form planetesimals in a broader disc region after increasing the DTG to at least 3% (see Appendix C).
Drążkowska & Alibert (2011) included a temperature evolution and perturbations around the ice line, using the Bitsch et al. (2015a) disc model, which makes planetesimal formation more efficient than in our model. Firstly, the perturbations around the ice line region delay pebble flux, and hence more planetesimals are formed. Secondly, the region where planetesimals are formed is larger due the disc temperature evolution, which shifts the ice line region. However, we did not include this in our simulations.
Drążkowska & Alibert (2011) focused on planetesimal formation at the water-ice line in contrast to our model, which features several evaporation fronts. Hence, our model sheds more light on dust pileup and hence the possibility of planetesimal formation at other ice lines other than the water-ice line.
Another key difference between our results and that of Drążkowska & Alibert (2011) is the metallicity effect, where the authors reported a difficulty in forming planetesimals at waterice line at solar metallicities unless the disc in non-irradiated. In the other disc models the authors tested, rather high DTG are needed to form planetesimals at the water-ice line. In contrast, our simulations reveal the minimum DTGs far below the solar values that support planetesimal formation at the water-ice line. This could be because we included particles with Stokes number larger than 0.001, while (Drążkowska & Alibert 2017) only included particles with St >0.01, which could also enhance our planetesimal formation efficiency at low metallicities. Despite the inherent differences discussed above, both our model and the Drążkowska & Alibert (2011) model highlight the sensitivity of planetesimal formation, especially at the ice line, to the disc parameters.
Other previous studies with results similar to ours include Schoonenberg et al. (2011) and Kalyaan et al. (2023), who find that planetesimal formation takes place at the water-ice line as a result of the traffic jam effect experienced by pebbles. However, in Schoonenberg et al. (2011), planetesimals were found to form in broad areas interior to the water-ice line, in contrast to our results, where planetesimals formed only at the water-ice line. This could be due to the fact that in Schoonenberg et al. (2011) the authors used a fragmentation velocity of 3 ms−1 for the dry silicates, which results in larger dust grains compared to the small grains interior to the waterice line in our simulations. The relatively large dust grains have higher Stokes numbers, which means they can easily reach the threshold for planetesimal formation. The major difference between our work and that of Kalyaan et al. (2023) is that, in their study, planetesimals were able to form at multiple locations in the outer disc regions primarily because the author included pressure bumps in their model, which allows an accumulation of particles and thus enhanced planetesimal formation (e.g. Johansen et al. 2007).
4 Discussion and summary
In this study, we explored a range of disc parameters to study how planetesimal formation might take place at ice lines, driven by drifting and evaporating pebbles, by simulating a full viscous disc evolution. Our key results have unveiled the minimum requirements of disc properties suitable for the formation of planetesimals, especially at solar and sub-solar metallicities.
In our simulations, we could not form planetesimals interior to the water-ice line despite the substantial accumulation of pebbles at the evaporation lines in the inner disc regions. Nevertheless, although the accumulated pebbles might not form planetesimals, the enhanced dust-to-gas ratios at the evaporation fronts could be beneficial for pebble accretion when a growing core accretes at those locations. This could be a possible formation pathway for hot and dense Jupiters around M dwarfs and could also be useful for understanding the origin of the heavy element content of certain exoplanets, including Jupiter.
In addition to the water-ice line, planetesimal formation can take place at the ice lines of volatile species in the outer disc regions. However, super-solar metallicities are required for planetesimals to form at those ice lines (see Appendix C). Hence, in addition to supporting planet formation, the planetesimals that formed at the ice lines in the outer regions could be the sources of planetesimal discs, such as those in the Kuiper belt in the Solar System (e.g. Eistrup et al. 2019). Additionally, Jupiter's core could have formed as a result of the presence of the water-ice line (Walsh et al. 2011; Savvidou & Bitsch 2021), although other formation pathways could also play a major role.
As shown in this study, the formation of planetesimals at the ice line is a spontaneous process once the Stokes number and the dust-to-gas ratio thresholds necessary for planetesimal formation are reached. This process can take place in the very early stages of disc evolution, which sets the stage for the early formation of planetary bodies (e.g. Manara et al. 2018; Savvidou & Bitsch 2023). In quiescent discs, planetesimal formation at the ice line is ephemeral because dust grains grow large and are lost more quickly via radial drift. In contrast, turbulent discs have better dust retention capabilities, and as such the planetesimal formation process continues until the pebble flux drops below the required thresholds for enhancing the dust-to-gas ratio at the water-ice line.
Furthermore, we have shown that planetesimal formation is a ubiquitous process, driven purely by the presence of the ice lines, that could take place in diverse disc environments, including stellar environments with sub-solar metallicities and an initial dust composition of at least 0.6%, corresponding to [Fe/H] = −0.6. However, only a few Earth masses of planetesimals form in such metal-poor stellar environments, which could also explain why the occurrence rate of super-Earths drops around [Fe/H] = −0.5 (Bashi & Zucker 2022).
Although the drift barrier is thought to initially lead to a rapid loss of solid material to the central star, this formidable process appears to be a holy grail for planetesimal formation at the water-ice line. Hence, the centimetre-sized pebbles might not be completely lost via rapid radial drift as previously thought since a substantial amount is instead transformed into planetesimals at the water-ice line. In our simulations, this process notably occurs in the early stages of disc evolution, which is beneficial for planet formation at the water-ice line because the formed planetesimals could subsequently accrete the incoming pebbles. However, because of the low fragmentation levels, it is very hard to make planetesimals in the inner disc (interior to the ice line). This is especially a problem for terrestrial planet formation and rocky super-Earth formation, unless their formation starts at or beyond the water-ice line, after which they could migrate inwards. However, this problem could be circumvented by a pressure perturbation that traps pebbles, leading to planetesimal formation and, later, pebble accretion in the interior disc regions.
The disc regions interior to the water-ice line exhibit high dust-to-gas ratios but very low Stokes numbers, which, again, is a problem for pebble accretion in this region. First of all, the very low Stokes numbers make pebble accretion inefficient. However, pebbles with very low Stokes numbers could be accreted along with the gas instead once the planets reach the gas accretion stage (Morbidelli et al. 2023; Bitsch & Mah 2023). Secondly, the dust grains in these region might just be the leftover pebbles that could not be converted into planetesimals at the ice line. This is especially possible if the ice line acts as an efficient site for planetesimal formation, where most of the pebbles are converted into planetesimals.
Our simulations lacked detailed grain dynamics that include the backreaction of the dust material on the gas and different fragmentation levels, which might not necessarily be as low as the 1 m s−1 assumed here interior to the water-ice line. Thus, this could significantly change the picture of planetesimal formation in the interior disc regions. Nevertheless, our results highlight the central role played by the evaporation fronts in planetesimal formation and consequences for the formation of terrestrial and rocky planets. Although we focused mainly on planetesimal formation at the different ice lines, planetesimal formation can take place elsewhere in the disc, for example in zonal flows (Johansen et al. 2011; Dittrich et al. 2013), in vortices (Raettig et al. 2015; Surville et al. 2016), and at the edges of the dead zone (Lyra et al. 2009). However, in the likelihood that the conditions for these mechanisms do not exist, the ice lines could be an ideal location for planetesimal formation and, hence, pebble accretion.
Acknowledgements
We thank the anonymous referee for the valuable comments, which helped us improve the quality of our paper. G.A. acknowledges the support from the Max Planck Society’s ARTEMIS – “African Research Talents Experiencing Mentorship In Science” program. J.M. and B.B. acknowledge the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (BI 1880/3-1). B.B. thanks the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support.
Appendix A Influence of grain size on planetesimal formation
 |
Fig. A.1 Planetesimal formation in a disc with a fixed grain fragmentation velocity of uftag = 1 m s−1, solar metallicity ([Fe/H] = 0), Mdisc = 0.1 M⊙, and a disc size rc = 100 au. Left: Quiescent disc with α = 10−4. Right: Turbulent disc with α = 10−3. |
In view of recent results that hint at lower fragmentation velocities, we performed additional simulations where the fragmentation velocity of dust grains is fixed at 1 ms−1 throughout the whole disc. The outcome is shown in Figure A.1.
We find that planetesimals can form at the water-ice line only in the case of a quiescent disc (αt = 10−4) due to the larger Stokes number of the pebbles. Since the Stokes number 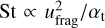 in the fragmentation limited regime (Birnstiel et al. 2009), dust grains of the same size will have a larger Stokes number in a quiescent disc than in a turbulent disc. This effect coupled with the low level of turbulence in the disc promotes the pileup of pebbles at the water-ice line and leads to the formation of planetesimals.
in the fragmentation limited regime (Birnstiel et al. 2009), dust grains of the same size will have a larger Stokes number in a quiescent disc than in a turbulent disc. This effect coupled with the low level of turbulence in the disc promotes the pileup of pebbles at the water-ice line and leads to the formation of planetesimals.
In contrast, small dust grains in a turbulent disc (e.g. αt = 10−3) are transported away quickly by the gas, thus preventing pebbles from piling up at ice lines and consequently hindering the formation of planetesimals.
Appendix B Disc composition
Abundances of elements included in our model (Asplund et al. 2009).
Molecules included in our model.
Appendix C Planetesimal formation at ice lines in discs with super-solar metallicities
We tested the possibility of planetesimal formation at super-solar metallicities at the ice lines of volatile species exterior to the water–ice line. The results are shown in Figure C.1, where we used DTGs of 0.02, 0.03, and 0.04, corresponding to the scaled [Fe/H] values 0.2, 0.3, and 0.4, respectively.
The top panel of Figure C.1 shows the simulations in a quiescent disc with αt = 10−4. Here, for the ice lines exterior to the water-ice line, planetesimal formation only takes place at the CO2 ice line, but this requires a DTG of at least 0.02. For the case of DTGs of 0.03 and 0.04, planetesimal formation takes place in broader disc regions exterior to the water-ice line because the increased DTGs lead to an increased traffic jam effect in the disc, in agreement with Drążkowska & Alibert (2011).
For the case of a turbulent disc with αt = 10−3 shown in the bottom panel of Figure C.1, planetesimal formation takes place at the CO2 ice line, which requires a lower DTG, 0.03, compared to the case of a quiescent disc with αt = 10−4. However, planetesimal formation in broader disc regions is still difficult for the case of αt = 10−3 despite the large amounts of solid material in the disc. As explained before, because of high viscosity, dust grains drift more slowly, which reduces the traffic jam effect, which hardly cascades beyond the ice lines compared to the quiescent disc. At the CH4 and CO ice lines, traces of planetesimals form when the dust-to-gas is increased to 0.04. Consequently it seems that discs with higher viscosity only allow planetesimal formation at discrete locations, while discs with lower viscosities allow planetesimal formation in broader ranges of the disc.
 |
Fig. C.1 Planetesimal formation at ice lines in discs at super-solar metallicities. The top and bottom panels show simulations with αt = 10−4 and αt = 10−3, respectively, in a disc with rc = 100 au. |
Appendix D How vertical settling affects planetesimal formation
The midplane dust-to-gas is influenced by the extent to which dust grains settle to the midplane through the vertical settling parameter αz, which in turn affects the planetesimal formation efficiency. Using vertical settling parameter αz = 10−3, we tested how weak grain settling affects planetesimal formation at solar and super-solar metallicities, as shown in Figures D.1 and D.2, respectively.
From Figure D.1, planetesimal formation can still take place in a less turbulent disc with αt = 10−4 compared to the turbulent disc with αt = 10−3. This is because, in the less turbulent disc, the large grains settle closer to the midplane compared to the more turbulent disc, which produces smaller size grains that hang farther above the midplane. This reduces the midplane dust-to-gas ratios, which makes planetesimal formation more difficult. However, increasing the disc metallicity to a supersolar value of [Fe/H] = 0.2 results in planetesimal formation in the more turbulent disc with αt = 10−3, as shown in Figure D.2, when the vertical settling parameter is set to αz = 10−3. At super-solar metallicity, there is enough solid material to increase the midplane dust-to-gas ratios, which supports planetesimal formation.
 |
Fig. D.1 Planetesimal formation in a disc with vertical settling parameter αz = 10−3, solar metallicity ([Fe/H] = 0), and a disc size rc = 100 au. |
 |
Fig. D.2 Planetesimal formation in a disc with vertical settling parameter αz = 10−3, super-solar metallicity ([Fe/H] = 0.2), and a disc size rc = 100 au. |
References
- Amelin, Y., Krot, A. N., Hutcheon, I. D., & Ulyanov, A. A. 2002, Science, 297, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Andama, G., Ndugu, N., Anguma, S. K., & Jurua, E. 2022, MNRAS, 512, 5278 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- August, P. C., Bean, J. L., Zhang, M., et al. 2023, ApJ, 953, L24 [CrossRef] [Google Scholar]
- Bashi, D., & Zucker, S. 2022, MNRAS, 510, 3449 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Morbidelli, A. 2023, Nat. Astron., 7, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Xue, Q., August, P. C., et al. 2023, Nature, 618, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2009, A&A, 503, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Andrews, S. M., Pinilla, P., & Kama, M. 2015, ApJ, 813, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Battistini, C. 2020, A&A, 633, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Mah, J. 2023, A&A, 679, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015a, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015b, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boley, K. M., Wang, J., Zinn, J. C., et al. 2021, AJ, 162, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkman, C. L., Weiss, L. M., Dai, F., et al. 2023, AJ, 165, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bitsch, B., Johansen, A., et al. 2018, ApJ, 856, 37 [Google Scholar]
- Buder, S., Asplund, M., Duong, L., et al. 2018, MNRAS, 478, 4513 [Google Scholar]
- Carrera, D., Johansen, A., & Davies, M. B. 2015, A&A, 579, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chambers, J. 2023, ApJ, 944, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, D.-C., Xie, J.-W., Zhou, J.-L., et al. 2022, AJ, 163, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J. 2010, ApJ, 723, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Connelly, J. N., Bizzarro, M., Krot, A. N., et al. 2012, Science, 338, 651 [Google Scholar]
- Dai, F., Schlaufman, K. C., Reggiani, H., et al. 2023, AJ, 166, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Dittrich, K., Klahr, H., & Johansen, A. 2013, ApJ, 763, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., Xie, J.-W., Zhou, J.-L., Zheng, Z., & Luo, A. 2018, PNAS, 115, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Drążkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [Google Scholar]
- Drążkowska, J., Alibert, Y., & Moore, B. 2016, A&A, 594, A105 [Google Scholar]
- Eistrup, C., Walsh, C., & van Dishoeck, E. F. 2019, A&A, 629, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
- Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [Google Scholar]
- Hellier, C., Anderson, D. R., Collier Cameron, A., et al. 2014, MNRAS, 440, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Hühn, L. A., & Bitsch, B. 2023, A&A, 676, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 616, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Bitsch, B., & Dasgupta, R. 2021, ApJ, 915, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, H., Macías, E., Guerra-Alvarado, O. M., & Carrasco-González, C. 2024, A&A, 682, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Johansen, A., Klahr, H., & Henning, T. 2011, A&A, 529, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [Google Scholar]
- Kalyaan, A., Pinilla, P., Krijt, S., et al. 2023, ApJ, 954, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kleine, T., Touboul, M., Bourdon, B., et al. 2009, Geochim. Cosmochim. Acta, 73, 5150 [Google Scholar]
- Kruijer, T. S., Kleine, T., Fischer-Gödde, M., Burkhardt, C., & Wieler, R. 2014, Earth Planet. Sci. Lett., 403, 317 [CrossRef] [Google Scholar]
- Kruijer, T. S., Burkhardt, C., Budde, G., & Kleine, T. 2017, PNAS, 114, 6712 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, R., & Youdin, A. N. 2021, ApJ, 919, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Line, M. R., Brogi, M., Bean, J. L., et al. 2021, Nature, 598, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [Google Scholar]
- Lyra, W., Johansen, A., Zsom, A., Klahr, H., & Piskunov, N. 2009, A&A, 497, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manara, C. F., Morbidelli, A., & Guillot, T. 2018, A&A, 618, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mills, S. M., Howard, A. W., Petigura, E. A., et al. 2019, AJ, 157, 198 [Google Scholar]
- Morbidelli, A. 2020, A&A, 638, A1 [Google Scholar]
- Morbidelli, A., Batygin, K., & Lega, E. 2023, A&A, 675, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sozzetti, A., et al. 2012, A&A, 543, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 557, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., Pascucci, I., Apai, D., Frasca, A., & Molenda-Żakowicz, J. 2016, AJ, 152, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, J., Savvidou, S., & Bitsch, B. 2021, A&A, 650, A185 [Google Scholar]
- Musiolik, G., & Wurm, G. 2019, ApJ, 873, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Ndugu, N., Bitsch, B., & Jurua, E. 2018, MNRAS, 474, 886 [Google Scholar]
- Okuzumi, S., Momose, M., Sirono, S.-I., Kobayashi, H., & Tanaka, H. 2016, ApJ, 821, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Onyett, I. J., Schiller, M., Makhatadze, G. V., et al. 2023, Nature, 619, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, S., Benneke, B., Ali-Dib, M., et al. 2023, Nature, 619, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Petigura, E. A., Marcy, G. W., Winn, J. N., et al. 2018, AJ, 155, 89 [Google Scholar]
- Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Klarmann, L., Birnstiel, T., et al. 2016, A&A, 585, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Pohl, A., Stammler, S. M., & Birnstiel, T. 2017, ApJ, 845, 68 [Google Scholar]
- Polanski, A. S., Crossfield, I. J. M., Burt, J. A., et al. 2021, AJ, 162, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Raettig, N., Klahr, H., & Lyra, W. 2015, ApJ, 804, 35 [Google Scholar]
- Rodríguez Martínez, R., Martin, D. V., Gaudi, B. S., et al. 2023, AJ, 166, 137 [CrossRef] [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ros, K., Johansen, A., Riipinen, I., & Schlesinger, D. 2019, A&A, 629, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savvidou, S., & Bitsch, B. 2021, A&A, 650, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savvidou, S., & Bitsch, B. 2023, A&A, 679, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, A. D., & Bitsch, B. 2021, A&A, 654, A71 [Google Scholar]
- Schoonenberg, D., Ormel, C. W., & Krijt, S. 2018, A&A, 620, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stammler, S. M., Birnstiel, T., Panić, O., Dullemond, C. P., & Dominik, C. 2017, A&A, 600, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stammler, S. M., Drążkowska, J., Birnstiel, T., et al. 2019, ApJ, 884, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Surville, C., Mayer, L., & Lin, D. N. C. 2016, ApJ, 831, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [Google Scholar]
- Wang, J., & Fischer, D. A. 2015, AJ, 149, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. M. Y., Morbidelli, A., Grimm, S. L., Stadel, J., & Brasser, R. 2023, Icarus, 396, 115497 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C.-C., Johansen, A., & Carrera, D. 2017, A&A, 606, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [Google Scholar]
- Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Planetesimal formation in a quiescent disc. Top: evolution of pebble and planetesimal surface densities for a nominal turbulent viscosity of αt = 10−4, a disc size of rc = 100 au, and different values of disc metallicity. Bottom: evolution of the Stokes numbers and the corresponding midplane dust-to-gas ratios. |
| In the text | |
 |
Fig. 2 Planetesimal formation in a turbulent disc. Top: evolution of pebble and planetesimal surface densities for a nominal turbulent viscosity of αt = 10−3, a disc size of rc = 100 au, and different values of disc metallicity. Bottom: evolution of the Stokes numbers and the corresponding midplane dust-to-gas ratios. |
| In the text | |
 |
Fig. 3 Metallicity dependence of planetesimal formation at the waterice line. |
| In the text | |
 |
Fig. 4 Lower limit of the DTG for planetesimal formation at the water-ice line in a disc with rc = 100 au. |
| In the text | |
 |
Fig. 5 Disc mass dependence of planetesimal formation at the waterice line in a disc environment with [Fe/H] = 0. The vertical dotted lines in the bottom panel show the points at which the curves start to level off, where planetesimals stop forming. |
| In the text | |
 |
Fig. 6 Disc size dependence of planetesimal formation at the water-ice line. The vertical dotted lines have the same meaning as in Fig. 5. |
| In the text | |
 |
Fig. 7 Disc turbulence dependence of planetesimal formation at the water-ice line in a disc with rc = 100 au and [Fe/H] = 0. Top: time evolution of the total solid mass without planetesimal formation taking place in the disc. Bottom: time evolution of the dust and pebble mass, including planetesimal formation in the disc. |
| In the text | |
 |
Fig. A.1 Planetesimal formation in a disc with a fixed grain fragmentation velocity of uftag = 1 m s−1, solar metallicity ([Fe/H] = 0), Mdisc = 0.1 M⊙, and a disc size rc = 100 au. Left: Quiescent disc with α = 10−4. Right: Turbulent disc with α = 10−3. |
| In the text | |
 |
Fig. C.1 Planetesimal formation at ice lines in discs at super-solar metallicities. The top and bottom panels show simulations with αt = 10−4 and αt = 10−3, respectively, in a disc with rc = 100 au. |
| In the text | |
 |
Fig. D.1 Planetesimal formation in a disc with vertical settling parameter αz = 10−3, solar metallicity ([Fe/H] = 0), and a disc size rc = 100 au. |
| In the text | |
 |
Fig. D.2 Planetesimal formation in a disc with vertical settling parameter αz = 10−3, super-solar metallicity ([Fe/H] = 0.2), and a disc size rc = 100 au. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



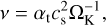
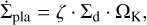
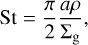
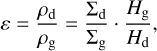
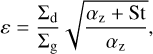
![${\rm{DTG}} = \sum {{{\rm{X}} \mathord{\left/ {\vphantom {{\rm{X}} {\rm{H}}}} \right. \kern-\nulldelimiterspace} {\rm{H}}} \cdot {\mu _{\rm{X}}} \times {{10}^{\left[ {{{\rm{X}} \mathord{\left/ {\vphantom {{\rm{X}} {\rm{H}}}} \right. \kern-\nulldelimiterspace} {\rm{H}}}} \right]}}} ,$](/articles/aa/full_html/2024/03/aa48899-23/aa48899-23-eq6.png)