| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 12 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202347910 | |
| Published online | 19 February 2024 | |
Search for duplicates of showers in the IAU MDC database
Methods and general results
1
Astronomical Observatory Institute, Faculty of Physics, A.M. University,
60-286
Poznań,
Poland
2
Astronomical Institute, Slovak Academy of Sciences, Tatranska Lomnica,
059 60
Vysoké Tatry,
Slovakia
3
RHEA Group,
2201 DZ
Noordwijk,
The Netherlands
4
ESA ESTEC,
2200 AG
Noordwijk,
The Netherlands
5
Astronomical Institute, Slovak Academy of Sciences,
845 04
Bratislava,
Slovakia
e-mail: maria.hajdukova@savba.sk
Received:
8
September
2023
Accepted:
16
November
2023
Context. The meteor shower database of the IAU Meteor Data Center (MDC) is used by the whole community of meteor astronomers. Observers submit both new and known meteor shower parameters to the MDC. Two types of problems may arise during the submission process: If a new observation of an already-known meteor shower is submitted as the discovery of a new shower, a duplicate shower will appear in the MDC. If the submission of a new set of parameters for an existing shower is incorrect, a false duplicate of a known meteor shower will appear in the MDC. The MDC database contains such duplicates and false duplicates, so it is desirable to detect them among the streams already in the database and those delivered to the database as new streams.
Aims. We aim to develop a method for objective detection of duplicates among meteor showers and to apply it to the MDC. The method will also enable us to verify whether various sets of parameters of the same shower are compatible and thus reveal the false duplicates.
Methods. We suggest two methods based on cluster analyses and two similarity functions among geocentric and heliocentric shower parameters collected in the MDC.
Results. We obtained a number of results of varying significance. Seven new showers represented by two or more parameter sets were discovered, revealing the duplicates we searched for. We found full agreement between our results and those reported in the MDC database for 30 showers. The multiple sets of parameters defining these showers are correct since they were identified as duplicates. For 20 showers, the same duplicates as given in the MDC were found only by one method. We found 27 showers for which the number of parameter sets found by both methods is close to the corresponding number in the MDC database. However, we found 56 showers listed in the MDC by more than one set of parameters for which no duplicates were found by either of the applied methods. These showers have false duplicates among their sets of parameters.
Conclusions. The obtained results confirm the effectiveness of the proposed approach of identifying duplicates. We have shown that in order to detect and verify duplicate meteor showers, it is possible to apply the objective proposal instead of the subjective approach used so far. We consider the identification of 83 problematic cases in the MDC database, among which at least some duplicates were misclassified, to be a particularly important result. The correction of these cases will significantly improve the content of the MDC database.
Key words: methods: data analysis / catalogs / meteorites, meteors, meteoroids
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In the case of asteroids (comets), it sometimes happens that observations of a new object, after some time, are linked to observations made in the past. Thus, the “new” object turns out to be an object already known. In meteor astronomy, such cases are not possible. In fact, meteoroids entering the Earth’s atmosphere are crushed and fall onto the Earth’s surface in the form of dust or sometimes larger fragments1. But in the case of the meteoroid streams, there exists an analogy to the rediscovery of asteroids known as duplicates.
In this work in particular, we address duplicate showers in the IAU Meteor Data Center (MDC) database. This database also includes showers whose average parameters were determined by two or more author teams. Hereafter, we refer to each set of the mean parameters published by one author team as a “solution”. Hence, in the remainder of this article, if there is more than one solution for a given shower in the MDC database, we use the term “multi-solution shower” (MSS), and we refer to each of these solutions as a “duplicate”. Otherwise, we use the term “single-solution shower” (SSS).
When the MDC list was created, no general criteria were adopted to distinguish whether a newly found solution is another solution of an already existing shower or if it is the first solution of a new shower. The individual author teams that contributed to the database proceeded according to their own approaches and evidently used different criteria.
However, an MSS solution might have been incorrectly assigned in the MDC and may actually be a stand-alone shower, that is, not a duplicate of the shower in question. Such a solution is called a “false duplicate”.
The duplicate showers we are searching for (i.e., the redundant showers in the MDC) are showers that were submitted as new autonomous showers to the MDC but are actually different solutions of previously submitted showers. We also refer to each such solution as a “duplicate”. Hence, a duplicate can be a solution of a given shower that is redundant and old (already existing in the database) or new (just supplied to the database). A correct list of showers in the MDC should not contain duplicate solutions across two different showers, nor should it include MSSs that consist of false duplicates.
If an autonomous shower is found to be a duplicate of another shower, its solution will be appended to that shower, and the autonomous shower will be moved to the list of removed showers. Of course, it is possible that some MSS solutions will be found to be duplicates of other showers and the rest of the MSS solutions will remain as duplicates of the original showers. In that case, the original shower will be retained, but with fewer solutions.
Within the MDC shower database, one can now find solutions that have been both correctly and incorrectly classified. To provide a clearer understanding of the terms used, we present a summary. The correctly classified solutions are (i) an autonomous solution of an SSS or (ii) a duplicate solution within an MSS (or simply a duplicate). The solutions that were classified incorrectly and need to be reclassified are (iii) false duplicate solutions, that is, a solution incorrectly classified as a duplicate solution of an MSS (after correction, these will be reclassified as a new SSS or as another solution of a different MSS) or (iv) false autonomous solutions (after correction, these will be reclassified as a duplicate solution of a different MSS).
The methods developed to identify comets and asteroids observed in successive apparitions have proven ineffective in determining whether one is dealing with duplicate meteor showers. The main obstacle is the single-apparition nature of the meteor phenomenon and the markedly lower precision of its observation.
Moreover, the geocentric and heliocentric parameters of a repeatedly observed meteoroid stream can differ significantly, as different observational techniques and weather conditions can cause independent observers to detect the shower meteors with different size distributions and/or in different periods of the shower’s activity. As a result, the new and old mean characteristics of a given shower can be quite different.
Hence, the question of whether one is dealing with a duplicate of a shower is not trivial. One can find several publications mentioning the occurrence of similar showers (“duplicates of showers” in our terminology) in the MDC database, for example, Holman & Jenniskens (2012), Andreić et al. (2014), Koukal (2017), Koseki (2020, 2023). Usually, authors provide a list of pairs that they consider to be similar showers and recommend removing the shower in question from the database and introducing it as another solution to an already known shower (e.g., Holman & Jenniskens 2012).
To date, however, the identification of a duplicate meteor shower and the associated recommendation have been based on more or less subjective considerations. Therefore, our work is focused on developing an objective method for detecting duplicates among meteor showers in the MDC database. Two approaches were used: a method based on orbital similarity and a method we developed called “maximum-sigmas” criterion based on direct comparison of selected geocentric and heliocentric shower parameters.
2 Meteor shower data used
As of December 2022, the MDC database contained data of 920 meteor showers, represented by 1385 solutions. For 252 showers, two or more solutions are available. The meteor data available from the MDC are not uniform, varying in the completeness of the averaged shower data. For all showers, the obligatory parameters are: the moment of activity, expressed by the ecliptic longitude of the Sun at the time of the shower observation; the geocentric equatorial coordinates of its radiant; and the corresponding geocentric velocity. For many showers, the corresponding averaged values of the orbital elements are also given, and for a relatively small number of showers, individual shower member data are available alongside the averaged data.
Hence, in order to make a full comparison of the results obtained in this study, we were limited to a subset of the MDC data that allows for the application of each method used. We utilized only the data from the list of established showers and the working list. Of the solutions on these lists, we rejected 195 either due to incomplete orbital data or because the orbital eccentricities corresponded to open orbits. We assumed that interstellar meteoroid stream solutions are not real and are the result of measurement uncertainties (Hajduková & Kornoš 2020). An additional eight solutions were removed due to the incorrect values of some parameters (e.g., orbital inclinations exceeding 180 degrees or because of a clear inconsistency between geocentric and heliocentric parameters). This inconsistency is due to the fact that although orbits with eccentricities e ≥ 1 were removed from our MDC sample, the values of the Öpik U and θ variables for some meteoroids (see Öpik 1976; Valsecchi et al. 1999), calculated on the basis of the geocentric parameters, clearly fall in the region corresponding to open orbits (see Fig. 1). The Öpik variables, U (in the units of the Earth’s velocity) and θ are defined in an instantaneous geocentric reference frame, and they respectively correspond to the geocentric velocity of the mete-oroid when encountering the Earth and to the angular elongation of the meteoroid geocentric radiant from the Earth’ apex. The values of the θ and U variables shown in Fig. 1 were calculated using the geocentric coordinates of the radiant and the speed of the meteoroids using the formulas given in Jopek et al. (1999b).
In the selected MDC dataset, 835 showers are represented by 1182 meteor shower solutions since the parameters of many showers were determined by more than one author team. More than one solution represents 185 showers. There are 532 solutions (45.0% of the total sample examined) that belong to these 185 MSSs. However, it has to be taken into account that we have no assurance that the grouping of the solutions in the MDC is, in all the listed showers, correct, since no objective method was available to detect the duplicates. Table 1 provides more details on the MSSs that occur in the surveyed sample of 1182 meteor shower solutions.
As is the case with the individual meteoroid orbits, the densities of meteor showers in near-ecliptical orbits are clearly higher, so we decided (following the idea given by Galligan 2001) to split the sample of 1182 shower solutions into two partitions. As can be seen in Fig. 2, the area containing orbits with small inclinations significantly dominates the study sample. It also contains many orbits with perihelion distances greater than 0.9 au. Partition one (P1) contained 498 shower solutions with orbits with inclinations in the range 0–40 deg. The second partition (P2) contained the other 684 shower solutions. In the remainder of this paper, we refer to these subsets of showers as P1 and P2 components.
Tables 2 and 3 give a full list of P1 and P2 MSSs (86 and 99, respectively) that were provided in the MDC database. The minimum number of solutions (duplicates) is, of course, two, with a maximum of 11 solutions for the Southern Taurids shower (02/STA)2. The SSS showers are not listed in Tables 2 or 3.
In the following sections, we describe our methodology and the results of the study. We reiterate that our aim was to find new MSSs and to assess whether the MSSs listed in Table 2 and Table 3 contain correctly classified duplicates.
In Tables 2 and 3, we introduce DHMin and 〈DH〉 columns. The DHMin column contains the smallest threshold values of orbital similarity corresponding to the DH function (Jopek 1993a) by which all members (all duplicates) of the MSSs given in Tables 2 and 3 can be identified using the cluster analysis and the single-linkage method. The 〈DH〉 column gives the arithmetic mean of the DH orbital similarity values calculated for all pairs of the given MSS. These values are related to the compactness of the MSS in question.
From a cursory analysis of the contents of the DHMin column, it is easy to see that for many MSSs that consist of only two duplicates, we are most likely dealing with cases of false duplicates. Using formulas (21) and (22) given in Table 9 in the Jopek & Bronikowska (2017), the plausible threshold values of orbital similarity for pairs of orbits taken from a set of 600 orbits are 0.022–0.025. In contrast, in Tables 2 and 3, we observed that for many MSSs with only two duplicates, the DHMin values are much larger. This observation justifies the revision we have undertaken of the MDC database in terms of the MSSs contained therein. Verification and searching for duplicates is an important topic, as abandoning such research would leave artifacts in the MDC database.
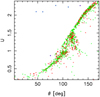 |
Fig. 1 Diagram of Öpik’s variables U (in units of the Earth’s velocity) and θ for meteor data from the MDC database. The red color indicates points for which ecliptic latitude |β| < 10 deg. The blue color indicates points for which the geocentric data are not consistent with the heliocentric data. These points lie in the area corresponding to open orbits. |
Single- and multi-solution showers in the used subset of 1182 meteor shower data.
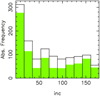 |
Fig. 2 Histogram of the inclination “inc” of 1182 orbits of the meteor showers used in our study. The green color depicts the orbits for which q > 0.9 au. Orbits with small inclination and high perihelion distances dominate the sample of 1182 meteor showers listed in the MDC as of December 16, 2022. |
3 Methodology for finding duplicates in the Meteor Data Center
A disadvantage of the approaches applied in this study is that we most often have to use individually averaged values of shower parameters. This means that the multidimensional averaging problem was substituted by a series of one-dimensional problems. It is well known (see Jopek 1986; Voloshchuk 1999; Voloshchuk & Kashcheev 1999; Williams 2001; Jopek et al. 2006, 2010b) that individual averaging can introduce some level of inconsistency between the geocentric and heliocentric parameters, and even between the heliocentric parameters themselves. For example, the individually averaged orbital elements q, a, and e may not necessarily satisfy the known formula q = a(l − e). The same problem occurs when the medians of the meteoroid stream parameters are used.
In our reduced sample of 1182 meteor shower data, each shower’s averaged geocentric and corresponding heliocentric parameters are given. Assuming that the impact of individual averaging of meteoroid parameters is not a significant obstacle to our idea, using these parameters, a search for duplicates among the MDC shower data can be done in a manner analogous to the search for streams among orbits of individual meteoroids. For this purpose, it is sufficient to use the cluster analysis methods, which have been used for years to search for meteoroid streams, with the difference being that, this time, the identification of groups in the MDC is made among the mean radiants or orbital elements or their combinations. As a result, the groups (MSS) thus identified will consist of the duplicates (solutions of MSSs) we are looking for.
We performed several cluster analyses among the 494 solutions in the P1 partition and among the 688 solutions collected in the P2 partition. We decided to search the two partitions separately so that the cluster analysis would be performed with threshold values of orbital similarity determined for each partition separately. This solution reduced the unfavorable influence coming from the domination of orbits with relatively small inclinations to the ecliptic in the studied sample of 1182 showers. We used a single-linkage method (a variant of the general hierarchical cluster analysis method) successfully used by a number of authors for the meteoroid stream identification or when searching for grouping among the asteroids: Southworth & Hawkins (1963), Lindblad (1971, 1992), Zappala et al. (1990, 1994), Zappalá et al. (1995), Jopek (1993b, 2020), Jopek et al. (1999a, 2003, 2010a).
List of 86 showers from partition P1 represented in the MDC by multiple solutions.
3.1 Method I: Cluster analysis among the orbital data
Our first approach (method I) takes advantage of the orbital similarity of meteoroids calculated by the D function. In the cluster analysis, a single-linkage method was used (see Southworth & Hawkins 1963; Jopek & Froeschle 1997). The orbital D distances were calculated by using the orbital similarity function DH described in Jopek (1993a), Williams et al. (2019). The orbital similarity thresholds were found separately for groups of M = 2,3,4,5, … members. The threshold for M = 10 was applied for all groups for which M > 10. All thresholds corresponded to a low probability (less than 1%) of chance grouping. Threshold values were calculated using the method presented in Jopek (2020). For P1 and P2 partitions, these values are listed in Table 4.
In the cluster analysis, we restricted the individual thresholds to the maximum value corresponding to M = 10. Such a decision is justified by the fact that only one of the MSSs in Table 1 contains more than ten duplicates, and our preliminary calculations showed that the threshold values of orbital similarity for the DH function determined for M > 10 were too large and led to results that were difficult to interpret. This may have to do with the limitations of the statistical approach for estimating threshold values, as mentioned in Jopek et al. (2003). As a reminder, the orbital similarity thresholds used in method I are only applicable in the cluster analysis performed with the single-linkage method. Of course, this does not apply to groups with only two members. The threshold values given in Table 4 corresponding to M = 2 do not depend on the choice of cluster analysis algorithm.
We note that any method to identify the duplicates will probably have to include a cluster analysis (e.g., single or other linkage procedures) since a linking of more than two solutions may be nontrivial. For example, if we consider three solutions A, B, and C and with the help of a method we find that B is the duplicate of A, solution B should therefore be one of the solutions of the shower that solution A belongs to. Further, if we find that C is the duplicate of B, solution C should therefore be a solution of the same shower as B, that is, the shower containing A. But, when applying the method to pair A and C we find that C is not a duplicate of A, a controversy occurs, as C should therefore not be the solution of the shower containing A. The single-linkage method can solve this problem.
List of 99 showers represented in the MDC partition P2 by multiple solutions.
Orbital DH similarity thresholds and their uncertainties applied in the search for duplicates among MDC shower data.
 |
Fig. 3 Cumulative distributions of the standard deviations of eight mean parameters of the showers in the IAU MDC with the Lookup Tables available. |
3.2 Method II: Maximum-sigma approach
In the second method (method II), we used the idea of similarity between two showers proposed by Koseki (2020). Koseki compared three shower parameters: the Sun-centered longitude and latitude of the ecliptic coordinates of the shower radiant and the ecliptic longitude of the Sun at the time of shower activity. To assess the similarity of two showers, Koseki calculated the differences between the relevant parameters and compared them with selected critical values. However, the author did not explain why he chose the critical values and not others, nor did he apply a cluster analysis to the whole dataset, thus limiting his research to comparing only two showers each time. In our view, this is a very limited approach. Therefore, in this study, we decided to extend Koseki’s approach by comparing both geocentric and heliocentric shower parameters as well as by performing cluster analysis. Moreover, in our approach, we have justified our choice of critical values of differences of the compared quantities.
When we want to determine whether a shower solution is an autonomous or a duplicate solution, we should be able to justify the difference between the parameters of that shower and the others in the database. So we examined a set of mean parameters, and in case of an autonomous shower, we demanded that the compared solutions significantly differ in at least one of these parameters.
To evaluate whether the difference among two values of the meteor shower parameter is significant, we adopted a similar approach to one that was recently applied in cosmology to reason that the Hubble constant determined by two methods is actually different (see e.g., Jones et al. 2020; Di Valentino et al. 2021; Perivolaropoulos & Skara 2021). Namely, the approach is the so-called three-sigma rule of thumb (or 3-σ rule). In empirical science, this rule expresses a conventional heuristic that nearly all values lie within three standard deviations of the mean (Kazmier 2003). With respect to meteor showers, it can therefore be argued that if the critical difference of two determinations of some shower’s parameter lies outside the ±3-σ interval, then the two meteor shower solutions being compared are not duplicates.
Unfortunately, the method based on the 3-σ difference of a parameter can only be used for a small fraction of the meteor showers since for the majority of solutions in the MDC database, the determination errors of the parameters are unknown. This circumstance forced us to propose and use a less exact but generally applicable method that we hereafter refer to as the “maximum-σ method”. We outline this method in the following paragraphs.
In December 2022, in addition to the shower average parameters, the MDC contained so-called lookup tables (see Hajduková et al. 2023) available for 127 showers. The contents of the Lookup Tables made it possible to calculate the standard deviations of the shower parameters of interest and, in a further step, to construct the cumulative distribution of these 1-σ values. In Fig. 3, these distributions are shown for the σ values of eight parameters. Specifically, panels a, b, c, and f–h of the figure show the distributions of the σ of the Sun-centered ecliptic coordinates of the mean radiant (λsc,β), the geocentric velocity (Vg), the argument of the perihelion (ω), the longitude of the ascending node (Ω), and the inclination (i), respectively. In these distributions, the steep increase is followed by a quasi-constant behavior (a plateau). This means that an essential part of the considered showers has the 1-σ value of a given mean parameter within the interval delimited by the beginning of the plateau.
In more detail, we found σ(λsc) = 5°, σ(β) = 3°, σ(Vg) = 2.5 km s−1, σ(ω) = 9°, σ(Ω) = 7.5°, and σ(i) = 5°. These values can be regarded as “maximum σs”. In Fig. 3, each maximum σ is indicated with an arrow. In the proposed method to find the duplicate solutions, the maximum σ, instead of 3σ, is regarded as a critical difference of mean values of a given parameter. If this difference is larger than the maximum σ of at least one parameter, then the examined solutions are either autonomous or false positives. Otherwise, the solutions are duplicates.
In the cumulative distributions of the 1-σs of the mean perihelion distance and eccentricity (Figs. 3d, e), there is no clear constant behavior (maybe, we could consider σ(q) = 0.08 au as the maximum deviation of q, but this is a relatively large value). These two parameters are therefore useless for our purpose and are therefore not taken into account.
Finally, we took into account the 1-σs of the Sun-centered ecliptic longitude, ecliptic latitude, geocentric velocity, argument of the perihelion, longitude of the ascending node, and inclination. Hence, we propose that two showers, A and B, are considered duplicates if the following conditions apply:
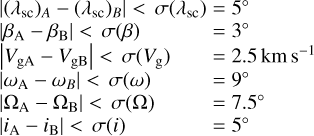 (1)
(1)
The maximum-σ criterion (1) allowed us to determine whether we were dealing with a duplicate or a false duplicate for a pair of solutions only. Therefore, in order to determine whether we were dealing with a group of duplicates of a given shower, it was necessary to apply criterion (1) in the cluster analysis. Analogous to method I, we used a cluster analysis algorithm based on a single-linkage procedure. In this approach, the inequalities (1) play an identical role to the D function in cluster analysis among orbital data. As in method I, cluster analyses were performed separately in P1 (494 orbits) and P2 (688 orbits).
3.3 Important differences between method I and method II
The duplicate search methods used in this study are not equivalent to each other. In our opinion, this is an advantageous property, as it strengthens the reliability of convergent results obtained by these methods. Both methods use the same cluster analysis algorithm, but the way of evaluating the similarity of the parameters of two meteor showers is fundamentally different.
In method I, the heliocentric Keplerian elements of the orbits are compared. With the DH function, differences in eccentricities, perihelion distances, and inclinations of the orbits are measured. However, the difference in the orientation of the apsidal lines is calculated as the difference in the angular positions of the perihelion points measured from the common point of the intersection of the two orbits. Figure 4 illustrates this issue. However, this means that an automatic search by method I will not always be able to identify the twin meteoroid streams or the northern and southern branches of showers as separate groups. The separation will have to be done “manually”. For example, such situations may be encountered in the case of the Orionids and eta-Aquariids showers or in the case of the Northern and Southern Taurids.
For method II, this kind of situation will not occur. The similarity of the showers is evaluated separately for each parameter, geocentric and heliocentric. We return to this issue in later sections of this paper.
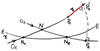 |
Fig. 4 Illustration of the difference in the orientation of the apsid lines in DH-function. The “E” stands for ecliptic; O1 denotes the orbit of the northern branch of the meteoroid stream; O2 is the orbit of the southern branch of the meteoroid stream; N1 and N2 are the ascending and descending nodes of the orbits where meteors have been observed, respectively; P1 and P2 denote perihelion points of both orbits; N is the common node of both orbits; π in red denotes the difference in the orientation of the apsid lines of the two orbits as measured from the common node N. |
Total number of multi-solution showers (NM) and number and percentage of duplicates (ND) among all MSSs identified in the 1182 showers of the MDC database by method I and method II.
4 General results
We have collected the general results in Table 5. Regarding method I, using the DH function, among 1182 orbits, 85 MSSs were found, comprising 456 duplicates. Some MSSs consist of only two solutions, but the largest consists of 62 solutions. The percentage of all duplicates was 38.7% of the shower solutions taken from our 1182 subset of the MDC.
As for method II, applying the maximum-sigma approach among 1182 showers, a total of 142 MSSs were identified, comprising 433 duplicates. They accounted for 36.6% of the MDC showers.
For the purpose of comparison, the last row of Table 5 shows the corresponding values calculated based on the data provided to the MDC by their authors. As suggested by these authors, it was found that in our subset of the MDC, 532 (45.0%) duplicates represent 185 multi-solution meteor showers.
This outcome allowed us to conclude that method I and method II do not produce results fully consistent with what is stated in the MDC. Compared to the MDC, our methods produce smaller numbers of MSS groups (85 and 142 in comparison to 185 stated in the MDC) that contain approximately 100 fewer duplicates (456 and 433 in comparison to 532 according to the MDC). These are significant differences in the number of MSSs as well as in the overall number of duplicates, suggesting that authors providing meteor data to the MDC quite often misclas-sify their showers. We found that dozens of the showers supplied to the MDC are unlikely to be duplicates (solutions of MSSs).
In Table 5, one can clearly see that method I and method II are not equivalent. This does not mean, however, that the methods we used produce completely inadequate results. As far as the total number of duplicates is concerned, both methods I and II gave convergent results: 456 and 433 duplicates, respectively. The results obtained differ in the number of MSSs identified, which means that the duplicates were classified into groups with different numbers of members (see Table 6). Before presenting and discussing the results we obtained, we emphasize that for method I, it was possible to estimate the probability of identifying MSS groups on a chance basis (it was less than 1%; see Sect. 3.1). For method II, we do not have such an estimate. Similarly, we have no idea what the reliability of the MSS findings made by the authors providing data to the MDC database is.
Number of NMSS of multi-solution showers consisting of NDU duplicates as identified by method I and method II.
5 Results and discussion: Less complex cases
More detailed results are given in Table 6. In the table, one can see how many of the MSSs were identified by method I and method II and how many were reported in the MDC database. One can also see that in the case of a small number of duplicates (NDU ≤ 4), the number of MSSs reported in the MDC and obtained by method II are far greater than the number of MSSs identified by method I. Nevertheless, the most numerous MSS group, containing 62 duplicates, was identified only by method I. At this stage, it is clear to us that the methods used in this study (and probably any other methods) cannot identify MSS groups as they are given in the MDC. Among other things, this is because the authors providing data to the MDC followed unknown, different criteria than we did when classifying the shower into a particular group. However, we are confident that the proposed approach of verifying the content of duplicates in the MDC database allows for the elimination of all obvious problematic cases, thus improving the MDC database.
In the following Sects. 5.1–5.2, we present results obtained directly (automatically) using our software. In Sects. 5.3–6.1, we present results that due to the nature of method I and the limitations of statistical determination of orbital similarity thresholds, required additional action on our part.
List of seven new MSSs found among the 1182 meteor data identified by both of the applied methods.
5.1 New multi-solution showers
Among the 1182 shower solutions taken from the MDC, we identified seven new MSSs, listed in Table 7. Two duplicates were identified in each new MSS. The reliability of this result is confirmed by the low threshold values of orbital similarity, corresponding to a less than 1 % probability of identifying each pair by chance by method I, and by the fact that they were also identified by method II.
5.2 Multi-solution showers fully confirmed in the present search
Table 8 lists the codes of 30 MSSs identified identically by the two methods we used. For each MSS, the same duplicates and the same number of duplicates were identified by each method exactly as they are listed in the MDC database.
As one can see in Table 8, the 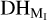 threshold values with which method I identified MSSs are always greater than the corresponding DHmin values. This supports the statement that among these MSSs, we are not dealing with false duplicates. The authors providing the data for these showers classified them in the right way. At the same time, this means that among the remaining 155 cases, some misclassification of duplicates is possible.
threshold values with which method I identified MSSs are always greater than the corresponding DHmin values. This supports the statement that among these MSSs, we are not dealing with false duplicates. The authors providing the data for these showers classified them in the right way. At the same time, this means that among the remaining 155 cases, some misclassification of duplicates is possible.
List of 30 MSSs for which exactly the same duplicates were found by both of the applied methods and as given in the MDC.
5.3 Multi-solution showers not identified in the present search
Among the 185 MSSs reported in the MDC database, 56 groups were not identified as MSSs by the two methods we used. Table 9 states the orbital DH similarity values of the showers associated with a given MSS. The DHmin is the smallest threshold that would have to be used in the cluster analysis for method I to identify all members of the given MSS as reported in the MDC database. The 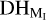 is the maximum threshold with which the given MSS should be identified by method I. We note that, as mentioned in Sect. 3.1, for the P1 and P2 partitions, the orbital similarity threshold values were determined separately.
is the maximum threshold with which the given MSS should be identified by method I. We note that, as mentioned in Sect. 3.1, for the P1 and P2 partitions, the orbital similarity threshold values were determined separately.
In Table 9, almost all the threshold values DHMin are too large (the values highlighted in italic) compared to the limiting 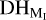 values, the maximum acceptable threshold value to reliably identify a group of the size in column NMDC when using method I. For example, DHmin = 0.315 for 128/00/MKA or DHmin = 0.798 for 0118/00/GNO are much to large because to identify an MSS with two duplicates only, the acceptable threshold value would be
values, the maximum acceptable threshold value to reliably identify a group of the size in column NMDC when using method I. For example, DHmin = 0.315 for 128/00/MKA or DHmin = 0.798 for 0118/00/GNO are much to large because to identify an MSS with two duplicates only, the acceptable threshold value would be 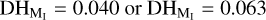 . Such small thresholds were used in method I in the cluster analysis, and they ensured that the probability of identifying a group of two duplicates by chance was less than 1%.
. Such small thresholds were used in method I in the cluster analysis, and they ensured that the probability of identifying a group of two duplicates by chance was less than 1%.
For 40 MSSs, all duplicates were rejected, and the rejected showers did not enter another MSS group. For 13 MSSs, after rejecting false duplicates, only single solutions remained, and they often entered another MSS group. As a result, we can claim that except for 3/00/SIA, 127/00/MCA, and 321/00/TCB, the remaining 53 MSSs listed in Table 9 should be considered as the false MSSs, and duplicates assigned with them should receive a stand-alone shower status in the MDC database.
We also recognize the possibility that in the MDC database, there are erroneous values among the shower parameters, the codes for which are given in Table 9. For this reason, it would be appropriate to ask (if possible) the authors providing the data to the MDC to check the correctness of the shower parameter values or the MSS classifications accordingly.
As an example of the problematic case, we present the details of the shower 152/NOC (Table 9, line 23) with very high DHmin = 0.644 value. In the MDC database the 152/NOC shower, named the Northern Daytime omega-Cetids, is represented by four solutions (listed in Table 10).
As can be seen in Table 10, compared to the others, the second solution clearly has different values of orbital angular elements. In particular, it has a much smaller orbit inclination value. Hence, in our opinion, the second solution was wrongly classified for this MSS shower. This solution was published by Nilsson (1964), and the shower was identified among radio-observed meteors. Nilsson did not propose a name for this shower, and in his paper in Table 4, he identified it as “Gr. 61.5.3”. This shower consists of ten members. Nilsson’s identification turned out to be correct, as it was confirmed by a completely different cluster analysis method by Jopek et al. (1999a). In Table 2 of this work, the stream was named mu-Arietids, and it is unclear to us why this shower was classified in Jenniskens (2006) as another solution of the 152/NOC shower. Additional cluster analysis performed without this solution showed that the three remaining solutions of the 152/NOC were identified exactly as given in the MDC database.
The example discussed above leads us to believe that we have a similar situation for many of the other showers listed in Table 10 as well. These will be presented and discussed in detail in our next publication.
List of 56 MSSs in the MDC for which no duplicates were found by any of the applied methods.
List of four solutions of averaged Keplerian orbital elements of the 152/NOC shower, the Northern Daytime omega-Cetids.
5.4 Multi-solution showers identified only by method II
The results presented in the previous sections were for MSSs identically identified or not identified by both method I and method II. In this section, we present results obtained only with method II. In Table 11, we report 20 MSS showers present in the MDC database and fully confirmed by method II only. At the same time, according to method I, none of the duplicates in question are members of any MSS.
The reason of it is that according to the MDC, the duplicates belonging to these showers are too dissimilar. Indeed, the acceptable DHMI thresholds given in Table 11 are always less than those that would have to be used in a cluster analysis to consider duplicates belonging to a given MSS as properly classified. However, unlike the contents of Table 9, the differences between the DHmin and DHMI values are noticeably smaller.
There are two possible reasons for this: either the thresholds used in method I are too stringent (which is possible), or method II is too tolerant. Method II does not take into account differences in the orbital elements e and q, which determine the shape and size of the orbit. It is almost certain that introducing these elements into the conditions (1) would at least reduce the number of MSSs listed in Table 11. However, other reasons are also possible, such as errors in the parameters of the showers supplied to the MDC base and a failure to meet the assumptions we mentioned in Sect. 3, namely, the impact of individual averaging of meteoroid parameters causing additional differences between the parameters to increase. Due to the small differences between the DHmin and DHMI values, at this stage of our research, we considered the MSS showers confirmed by either method to be fully confirmed.
List of 20 MSSs for which exactly the same duplicates as given in the MDC were found only by method II.
6 Results and discussion: more difficult cases
The inconsistencies in the results discussed in the previous section do not include all the inconsistencies we encountered in our study. We present the remaining inconsistencies in the following subsections.
List of seven MSSs for which the number of the same duplicates found by method I and method II is close to the corresponding number in the MDC database.
6.1 Sufficiently confirmed multi-solution showers
The results given in the previous sections were selected “automatically” using our software. In this section, we present results confirming the existence of a given MSS in the MDC database. However, some of them were not confirmed automatically by both methods. Sometimes the members of the given MSS were picked out of the more complex identified groups in a manual manner.
Table 12 lists seven MSSs identified automatically and for which the numbers of duplicates identified by both methods are more or less close to the number reported in the MDC database. Compared to what is given in the MDC database, the differences are quantitative, consisting of deleting (or adding) new members from (to) the group. Hence, in our opinion, all MSSs listed in Table 12 can be considered sufficiently confirmed.
6.2 Multi-solution showers confirmed after manual action
In a dozen cases, MSS identification required manual action in the results obtained automatically. That is, we are referring to MSSs identified with a distinctly larger number of duplicates, which includes other groups treated as separate MSSs in the MDC database. An extreme case was 2/00/STA (Southern Taurids), for which method I identified 62 duplicates.
The actual meteoroid streams may have a different structure in the parameter space used in method I and method II. These parameters may occupy volumes that resemble hyper-spheres in five-dimensional space (Geminids), but equally they may well occupy more extended volumes (Taurids). The reason for the complexity of the results discussed in this section is related to, among other things, the property of the single-linkage algorithm used in the cluster analysis in both methods. With this algorithm, the so-called chain effect is possible. As a result, successively connected group members form a chain-like structure, and if too high a threshold value is applied, it leads to the identification of an unrealistic group of orbits. For these reasons, determining the correct threshold values of orbital similarity by statistical methods but taking into account only the abundance of the meteoroid stream may lead to unrealistic results.
This chain effect is clearly stronger in the case of method I for the shower 2/00/STA (Southern Taurids). An ecliptic group of 62 duplicates was identified by method I, including all the duplicates of the Northern and Southern Taurids showers and the 41 duplicates belonging to a dozen other MSSs. The variation in the results is also attributable to the properties of the similarity metrics used by both methods, as we mentioned in Sect. 3.3.
Table 13 contains a list of 27 MSSs obtained manually from results identified automatically. All the MSSs in this table can be considered confirmed, but we believe it would be best to examine each of them in a separate detailed study.
List of 27 MSSs for which, after manual action, the number of the same duplicates found by method I and method II is close to the corresponding number in the MDC database.
7 Conclusion and discussion of future action
We used two methods to search for MSSs among 1182 meteor shower solutions selected from the MDC database. The obtained results confirmed the effectiveness of the proposed approach of identifying duplicates. We show that in order to detect and verify duplicate meteor showers, it is possible to apply the objective proposal instead of the subjective approach that has been used up to now.
However, it appears revealing the duplicate showers is not a simple task. One must confront a wide variety of properties of various meteor showers. Not only are there known compact showers with parameters ranging in a relatively narrow interval, but there are also showers with relatively largely dispersed parameters. Sometimes a shower possesses some structural features, and it is only a matter of convention to regard these features as the substructures of a given shower or as autonomous showers.
In our study, a number of results of varying significance were obtained: (i) Seven new MSSs represented by two or more parameter sets were discovered. (ii) For 30 MSSs, there was full agreement between our results and those reported in the MDC database. (iii) For 20 MSSs the same duplicates as given in the MDC were found only by one method. (iv) We found 27 MSSs for which the number of the same duplicates found by our two methods is close to the corresponding number in the MDC database. (v) For 56 MSSs listed in the MDC, no duplicates were found by either of the applied methods.
We consider the identification of 27 plus 56 problematic cases in the MDC database, among which at least some duplicates were misclassified, to be a particularly important result. The correction of these cases will significantly improve the content of the MDC database. As shown in Sect. 5.3, such an adjustment is possible, but it always requires a meticulous approach, so we will pursue the adjustment in a subsequent study.
Determining the correct duplicates of the MSS is important when it comes to giving a shower its established status and, consequently, its official shower name. In Hajduková et al. (2023), one of the criteria that must be met for this purpose is that the shower must be represented by at least two sets of parameters (duplicates) determined by independent authors. Nevertheless, we are convinced that our work helps identify the problems related to the duplicity problem, and a wide discussion in the meteor-research community will follow.
Acknowledgements
This work was supported, in part, by the VEGA – Slovak Grant Agency for Science, grant no. 2/0009/22. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
References
- Andreić, Ž., Šegon, D., & Vida, D. 2014, in Proceedings of the International Meteor Conference, Giron, France, 18–21 September 2014, eds. J. L. Rault, & P. Roggemans, 126 [Google Scholar]
- Di Valentino, E., Mena, O., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Galligan, D. P. 2001, MNRAS, 327, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Hajduková, M., & Kornos, L. 2020, Planet. Space Sci., 190, 104965 [CrossRef] [Google Scholar]
- Hajduková, M., Rudawska, R., Jopek, T. J., et al. 2023, A&A, 671, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, D., & Jenniskens, P. 2012, WGN, J. Int. Meteor Organ., 40, 166 [NASA ADS] [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge University Press) [CrossRef] [Google Scholar]
- Jones, D., Casertano, S., Filippenko, A. V., et al. 2020, Tension at the Breaking Point: Uncovering New Physics Through a Two-Rung Distance Ladder Measurement of the Hubble Constant, HST Proposal, Cycle 28, 16269 [Google Scholar]
- Jopek, T. J. 1986, PhD thesis, A.M. University, Poznan, Poland [Google Scholar]
- Jopek, T. J. 1993a, Icarus, 106, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J. 1993b, in Meteoroids and their Parent Bodies, Proceedings of the International Astronomical Symposium held at Smolenice, Slovakia, July 6–12, 1992, eds. J. Stohl, & I. P. Williams (Astronomical Institute of the Slovak Academy of Sciences, 1993), 269 [Google Scholar]
- Jopek, T. J. 2020, MNRAS, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., & Bronikowska, M. 2017, Planet. Space Sci., 143, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., & Froeschle, C. 1997, A&A, 320, 631 [NASA ADS] [Google Scholar]
- Jopek, T. J., & Kanuchová, Z. 2017, Planet. Space Sci., 143, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., Valsecchi, G. B., & Froeschle, C. 1999a, in Meteoroids 1998, Proceedings of the International Conference held at Tatranska Lomnica, Slovakia, August 17–21, 1998, eds. W. J. Baggaley, & V. Porubcan (Astronomical Institute of the Slovak Academy of Sciences) [Google Scholar]
- Jopek, T. J., Valsecchi, G. B., & Froeschle, C. 1999b, MNRAS, 304, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., Valsecchi, G. B., & Froeschlé, C. 2003, MNRAS, 344, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., Rudawska, R., & Pretka-Ziomek, H. 2006, MNRAS, 371, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., Koten, P., & Pecina, P. 2010a, MNRAS, 404, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. T., Rudawska, R., & Ziomek-Pretka, H. 2010b, in Proc. of the International Meteor Conference, 27th IMC, Sachticka, Slovakia, 2008, 91 [Google Scholar]
- Jopek, T. J., Hajduková, M., Rudawska, R., et al. 2023, New Astron., Rev., 96, 101671 [NASA ADS] [CrossRef] [Google Scholar]
- Kazmier, L. 2003, Business statistics: based on Schaum’s outline of theory and problems of business statistics (McGraw-Hill) [Google Scholar]
- Koseki, M. 2020, eMeteorNews, 5, 93 [NASA ADS] [Google Scholar]
- Koseki, M. 2023, eMeteorNews, 8, 337 [NASA ADS] [Google Scholar]
- Koukal, J. 2017, eMeteorNews, 2, 27 [NASA ADS] [Google Scholar]
- Lindblad, B. A. 1971, Smithsonian Contrib. Astrophys., 12, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, B. A. 1992, in Asteroids, Comets, Meteors 1991, eds. A. W. Harris, & E. Bowell, 363 [Google Scholar]
- Nilsson, C. S. 1964, Austr. J. Phys., 17, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Öpik, E. J. 1976, Interplanetary Encounters - Close-Range Gravitational Interactions. Developments in Solar System and Space Science (Amsterdam: Elsevier Scientific Publishing Co.), 2, 160 [Google Scholar]
- Perivolaropoulos, L., & Skara, F. 2021, Phys. Rev. D, 104, 123511 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, R. B., & Hawkins, G. S. 1963, Smithsonian Contrib. Astrophys., 7, 261 [Google Scholar]
- Spurný, P., Ceplecha, Z., & Borovicka, J. 1991, WGN, J. Int. Meteor Organ., 19, 13 [Google Scholar]
- Valsecchi, G. B., Jopek, T. J., & Froeschle, C. 1999, MNRAS, 304, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Voloshchuk, Y. 1999, in Meteoroids 1998, Proceedings of the International Conference held at Tatranska Lomnica, Slovakia, August 17–21, 1998, eds. W. J. Baggaley, & V. Porubcan (Astronomical Institute of the Slovak Academy of Sciences), 199 [Google Scholar]
- Voloshchuk, Y. I., & Kashcheev, B. L. 1999, Solar Syst. Res., 33, 302 [NASA ADS] [Google Scholar]
- Williams, I. P. 2001, in Meteoroids 2001 Conference, ed. B. Warmbein, ESA Special Publication, 495, 33 [NASA ADS] [Google Scholar]
- Williams, I. P., Jopek, T. J., Rudawska, R., Tóth, J., & Kornos, L. 2019, in Meteoroids: Sources of Meteors on Earth and Beyond, eds. G. O. Ryabova, D. J. Asher, & M. J. Campbell-Brown (Cambridge UK: Cambridge University Press), 210 [Google Scholar]
- Zappala, V., Cellino, A., Farinella, P., & Knezevic, Z. 1990, AJ, 100, 2030 [CrossRef] [Google Scholar]
- Zappala, V., Cellino, A., Farinella, P., & Milani, A. 1994, AJ, 107, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Zappalá, V., Bendjoya, P., Cellino, A., Farinella, P., & Froeschle, C. 1995, Icarus, 116, 291 [CrossRef] [Google Scholar]
However, there are exceptions – the occurrence of an Earth-grazing fireball, a very bright meteoroid that enters Earth’s atmosphere and leaves again, see e.g. Spurný et al. (1991).
All the showers we used were named using the old rules of naming and coding meteoroid streams valid until August 2022 (see Jopek et al. 2023).
All Tables
Single- and multi-solution showers in the used subset of 1182 meteor shower data.
List of 86 showers from partition P1 represented in the MDC by multiple solutions.
Orbital DH similarity thresholds and their uncertainties applied in the search for duplicates among MDC shower data.
Total number of multi-solution showers (NM) and number and percentage of duplicates (ND) among all MSSs identified in the 1182 showers of the MDC database by method I and method II.
Number of NMSS of multi-solution showers consisting of NDU duplicates as identified by method I and method II.
List of seven new MSSs found among the 1182 meteor data identified by both of the applied methods.
List of 30 MSSs for which exactly the same duplicates were found by both of the applied methods and as given in the MDC.
List of 56 MSSs in the MDC for which no duplicates were found by any of the applied methods.
List of four solutions of averaged Keplerian orbital elements of the 152/NOC shower, the Northern Daytime omega-Cetids.
List of 20 MSSs for which exactly the same duplicates as given in the MDC were found only by method II.
List of seven MSSs for which the number of the same duplicates found by method I and method II is close to the corresponding number in the MDC database.
List of 27 MSSs for which, after manual action, the number of the same duplicates found by method I and method II is close to the corresponding number in the MDC database.
All Figures
 |
Fig. 1 Diagram of Öpik’s variables U (in units of the Earth’s velocity) and θ for meteor data from the MDC database. The red color indicates points for which ecliptic latitude |β| < 10 deg. The blue color indicates points for which the geocentric data are not consistent with the heliocentric data. These points lie in the area corresponding to open orbits. |
| In the text | |
 |
Fig. 2 Histogram of the inclination “inc” of 1182 orbits of the meteor showers used in our study. The green color depicts the orbits for which q > 0.9 au. Orbits with small inclination and high perihelion distances dominate the sample of 1182 meteor showers listed in the MDC as of December 16, 2022. |
| In the text | |
 |
Fig. 3 Cumulative distributions of the standard deviations of eight mean parameters of the showers in the IAU MDC with the Lookup Tables available. |
| In the text | |
 |
Fig. 4 Illustration of the difference in the orientation of the apsid lines in DH-function. The “E” stands for ecliptic; O1 denotes the orbit of the northern branch of the meteoroid stream; O2 is the orbit of the southern branch of the meteoroid stream; N1 and N2 are the ascending and descending nodes of the orbits where meteors have been observed, respectively; P1 and P2 denote perihelion points of both orbits; N is the common node of both orbits; π in red denotes the difference in the orientation of the apsid lines of the two orbits as measured from the common node N. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


