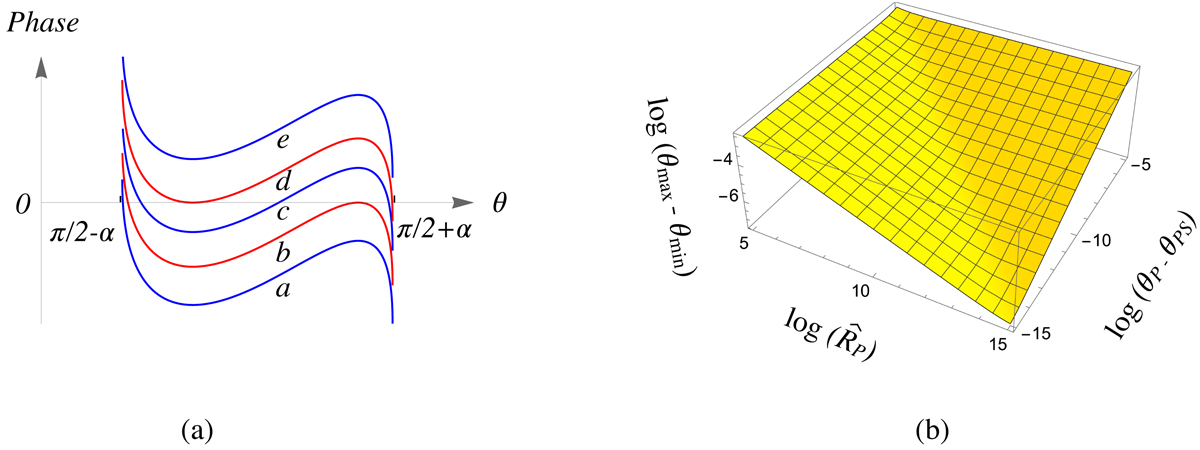
Phase of the kernel of the integral over θ and its critical points. (a) Dependence on the colatitude, θ, of the phase of the type of oscillating exponential that is encountered after we superpose the contributions of the constituent rotating rings of the source distribution that have the same colatitude but differing radii (see Sect. 2.2). The curves a–e correspond to successively increasing values of the azimuthal coordinate of the observation point, φ_P. Note that for curves b and d (shown in red), this phase vanishes at one of its turning points. (b) Dependence of the separation between the locations of the maximum and minimum of a phase, θ_max − θ_min, with nearby turning points on the distance of the observer from the source, , and on the departure, θ_P − θ_PS, of the colatitude of the observer, θ_P, from the critical colatitude, θ_PS, at which the maximum and minimum of such a phase coalesce. This figure shows that θ_max − θ_min decreases as with increasing distance when .