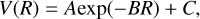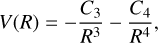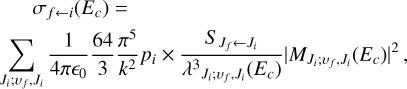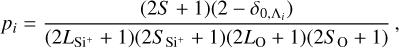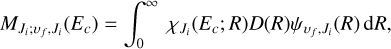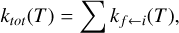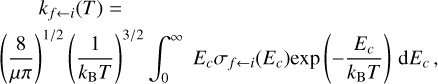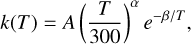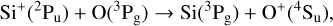EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A25 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A25
Number of page(s) 7
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202245326
Published online 28 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Silicon (Si) is one of the most abundant elements in cosmic dust. A significant amount of Si is injected into the atmosphere above 80 km by meteoric ablation (Plane et al. 2016). Tentative spectroscopic evidence was obtained using the Solar Occultation For Ice Experiment (SOFIE) instrument on board the Aeronomy of Ice in the Mesosphere (AIM) satellite showing that meteoric smoke particles (MSPs) below 85 km are composed of Fe-Mg-silicates (Hervig et al. 2012). Extraterrestrial neutral silicon compounds have not yet been detected in the mesosphere or lower thermosphere (MLT) region between 70 and 120 km (Kopp et al. 1995; Grebowsky & Aikin 2002), but the Si+ ions have been measured by the rocket-borne mass spectrometry and have consistently been shown to be the major meteoric ion around 110 km.

Interstellar Si chemistry was first discussed in detail by Turner & Dalgarno (1977), who estimated the abundances of Si-containing species, including SiH, SiH+, SiN and so on, in diffuse interstellar clouds. Si chemistry has aroused great attention in planet-host stars (Brugamyer et al. 2011), variable star IRC+10216 (Takano et al. 1992), the orion nebula (Rubin et al. 1993), the upper stellar atmosphere (Glassgold et al. 1986), and photodissociation regions (Walmsley et al. 1999). In widely distributed interstellar molecular clouds, the elemental abundance of Si is twice that of S and only one order of magnitude less than C, N, or O. In dense clouds, the Si+ ions are easily generated from dissociative shocks under suitable conditions (Neufeld & Dalgarno 1989). In the diffuse interstellar medium, silicon with an ionisation potential of 8.15 eV exists primarily as ions (Stancil et al. 2000), and the oxygen atoms are also prevalently in existence, which may provide conditions for the process of the SiO+ radiative association. SiO+ has been photographed by spectrograph (Singh et al. 1973) and plays a significant role in the chemistry of diffuse interstellar clouds (Turner & Dalgarno 1977; Langer & Glassgold 1990) and hot circumstellar regions (Scalo & Slavsky 1980; Clegg et al. 1983). To attain a better understanding of the Si chemistry in the interstellar medium, possible pathways to the formation of SiO+ are worth considering, one example being radiative association.

Radiative association is a reaction where two species collide with each other to form an intermediate that is stabilised via the emission of a photon. It is the only association process that occurs in low-density interstellar space (Gerlich & Horning 1992). Radiative association is difficult to induce under experimental conditions, and so rate coefficients have only been successfully measured for a few cases. At present, there have been no successful attempts to bring about the formation of neutral diatomic molecules through radiative association (Nyman et al. 2015), which mainly results from the fact that this process can only be accomplished using ion traps or the ion cyclotron resonance apparatus, requiring that at least one of the colliding species be charged. However, a great number of traditional theories and methods, including the classical method (Gustafsson 2013; Nyman et al. 2015; Kathir et al. 2017), semiclassical (SC) method (Bates 1951; Gustafsson & Forrey 2019; Andreazza et al. 2012; Andreazza & de Almeida 2014; Zámečníková et al. 2020), quantum mechanical (QM) method (Golubev et al. 2013; Antipov et al. 2009; Barinovs & van Hemert 2006; Franz et al. 2011; Gustafsson et al. 2014; Nyman et al. 2015; Andreazza et al. 2016; Babb & McLaughlin 2017; Kathir et al. 2017; Szabó & Gustafsson 2019; Zámečníková et al. 2020; Babb et al. 2019), Breit–Wigner theory (Breit & Wigner 1936; Bain & Bardsley 1972; Zámečníková et al. 2020; Szabo et al. 2021), and optical potential method (Liu et al. 2010; Mies 1969; Nyman et al. 2015; Liu et al. 2009), have been developed to compute the radiative association cross sections and rate coefficients. These methods have been extensively used to study small molecules in astrophysical environments, especially for diatomic molecules such as MgO (Bai et al. 2021), 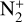N2+${\rm{N}}_2^ + $ (Qin et al. 2021), CS (Forrey et al. 2018), AlO (Bai et al. 2022), CN (Zhang et al. 2022), CO (Meng et al. 2022), CF+ (Öström et al. 2016), NaCl (Šimsová-Zámecníková et al. 2022), BeH+ and BeD+ (Szabo et al. 2021) and so on. Furthermore, recent developments of the theories and methods, including the Sturmian quantum kinetic theory (Forrey 2015), the surface-hopping model of spontaneous electronic transitions (Szabó & Gustafsson 2017), the extension of radiative association to local thermal nonequilibrium (Gustafsson & Forrey 2019), and the treatment of non-adiabatic couplings (Gustafsson 2020), have led to new insights into radiative association.

As early as 1995, Andreazza et al. (1995) calculated the rate coefficient for the radiative association of SiO+, considering the A 2Π → X 2Σ+ transition based on ab initio potential energy curves (PECs) of the X 2Σ+ and A 2Π states and the transition dipole moment (TDM) for the A 2Π → X 2Σ+ system (Werner et al. 1982). The rate coefficient for the A 2Π → X 2Σ+ transition was corrected in 1997 (Andreazza et al. 1997). This rate coefficient was later used to model the chemical evolution of SiO+ in the ejecta of Population III supernovae (SNe; Cherchneff & Dwek 2009) and to investigate the molecular chemistry of Type Ibc SNe (Liljegren et al. 2022). However, the PECs and TDM used by Andreazza et al. (1995) were obtained using the multi-configuration self-consistent-field (MCSCF) method whose accuracy is insufficient relative to the state-of-the-art ab initio methods, such as the multi-reference configuration interaction (MRCI) method, which is widely used nowadays. Furthermore, other radiative association processes of SiO+ in addition to the A 2Π → X 2Σ+ transition may also be important. We therefore revisit the radiative association of SiO+ by considering all possible radiative association processes correlating to the collision of Si+ (3s23p 2Pu) and O(2s22p4 3Pg) using the state-of-the-art ab initio PECs and TDMs.

In recent years, PECs and TDMs of SiO+ have been studied by many researchers. Earlier, PECs of the SiO+ cation for the low-lying electronic states and dipole-allowed TDMs between doublet states of SiO+ were comprehensively computed by Cai & François (1999) with the internally contracted multi-reference configuration interaction (icMRCI) method. Subsequently, the multi-reference singles and doubles configuration interaction (MRDCI) method was used by Chattopadhyaya et al. (2003) to calculate PECs, spectroscopic parameters, and TDMs for several low-lying electronic states of SiO+. Moreover, Shi et al. (2012) presented a high-level study for eight electronic states of SiO+ using the MRCI method. More recently, Qin et al. (2020) used the icMRCI method to investigate the PECs and TDMs for 17 low-lying electronic states of SiO+ with the consideration of the Davidson correction, the basis set extrapolation, core-valence correction, and scalar relativistic correction. The PECs and TDMs obtained by Qin et al. (2020) are adopted in the present work to explore the cross sections and rate coefficients for the formation of SiO+ by radiative association.

This paper is organised as follows. Ab initio data for PECs, dipole-allowed TDMs, and permanent dipole moments (PDMs) are presented in Sect. 2, as well as the theory and methods for the radiative association. The cross sections and rate coefficients of SiO+ are given and discussed in Sect. 3. Finally, a conclusion is drawn in Sect. 4.

Table 1

Local maximums at the PECs of the 2 2Π, 2 2Σ−, and 1 4Π states.

Table 2

Radiative association processes studied in this work for SiO+.

2 Theory and methods

2.1 Potential energy and transition moment curves

For SiO+, there are 12 electronic states correlating to the Si+ (3s23p 2Pu) + O(2s22p4 3Pg) dissociation limit; here, we consider 10 of these, including the A 2Π, X 2Σ+, 1 4Σ+, 1 4Π, 1 4Σ−, 1 4∆, 2 2Π, 2 2Σ−, 1 2∆ and 1 2Σ− states. The 2 4Π state is repulsive and the 2 4Σ− state has a shallow potential energy well above its dissociation limit. The transitions from these two states are expected to contribute little to the radiative association of SiO+ and are not taken into account here. Some local maximums on the PECs of the 2 2Π, 2 2Σ− and 1 4Π states are presented in Table 1 to allow a better understanding of the subsequent radiative association cross sections and rate coefficients. The PECs and TDMs are adopted from ab initio calculations by Qin et al. (2020) and presented in Fig. 1. In addition, we also consider the permanent dipole transitions of SiO+, which also contribute to the radiative association of SiO+. The PDMs for the A 2Π → A 2Π, X 2Σ+ → X 2Σ+, 1 4Σ+ → 1 4Σ+, 1 4Π → 1 4Π, 1 4Σ− → 1 4Σ− and 1 4∆ → 1 4∆ transitions are calculated at the icMRCI + Q/aug-cc-pV6Z level of theory, as displayed in Fig. 2, which is the same level at which TDMs were computed by Qin et al. (2020). Overall, we concentrate on 18 radiative association processes, as listed in Table 2.

For the calculation of cross sections and rate coefficients, PECs and TDMs must be extrapolated over the short and long range of internuclear distance R. In this work, the PECs for R < 1.1 Å are extrapolated using the following function:

V(R)=Aexp(−BR)+C,$V\left( R \right) = A\exp \left( { - BR} \right) + C,$(1)

where A, B, and C are fitting parameters. The cubic spline was used to interpolate the ab initio points. To ensure a continuous and smooth potential energy curve, the PECs can be extrapolated using the following function for the long-range region:

V(R)=−C3R3−C4R4,$V\left( R \right) = - {{{C_3}} \over {{R^3}}} - {{{C_4}} \over {{R^4}}},$(2)

where Cз and C4 are state-dependent coefficients, which were estimated by fitting ab initio points in this work. TDMs and PDMs are also extrapolated using Eqs. (1) and (2).

thumbnail Fig. 1

Potential energy curves (a) and transition dipole moments (b) for SiO+ which are taken from Qin et al. (2020).
thumbnail Fig. 2

Permanent dipole moments for the electronic states of SiO+ computed in this work.

2.2 Radiative association cross sections

The quantum mechanical expression of the radiative association cross sections is shown as follows:

σf←i(Ec)=∑Ji,υf,Ji14πϵ0643π5k2pi×SJf←Jiλ3Ji;υf,Ji(Ec)| MJi;υf,Ji(Ec) |2,$\matrix{ {{\sigma _{f \leftarrow i}}\left( {{E_c}} \right) = } \hfill \cr {\sum\limits_{{J_i},{\upsilon _f},{J_i}} {{1 \over {4\pi {_0}}}{{64} \over 3}{{{\pi ^5}} \over {{k^2}}}{p_i} \times {{{S_{{J_f} \leftarrow {J_i}}}} \over {{\lambda ^3}_{{J_i};{\upsilon _f},{J_i}}\left( {{E_c}} \right)}}{{\left| {{M_{{J_i};{\upsilon _f},{J_i}}}\left( {{E_c}} \right)} \right|}^2},} } \hfill \cr } $(3)

where the symbol i donates the physical quantity of the initial electronic state, while ƒ represents the physical quantity of the final electronic state. ϵ0 is the vacuum permittivity, k2 = 2Ecµ/ħ2, Ec is the collision energy, µ is the reduced mass of SiO+, and ħ is the reduced Planck constant. Furthermore, 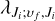λJi;υf,Ji${\lambda _{{J_i};{\upsilon _f},{J_i}}}$ is the wavelength of the emitted photon, and 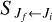SJf←Ji${S_{{J_f} \leftarrow {J_i}}}$ is the Hönl-London factor (Watson 2008; Hansson & Watson 2005). Here, pi is the probability of collision for the initial electronic state i, given by

pi=(2S+1)(2−δ0,Λi)(2LSi++1)(2SSi++1)(2So+1),${p_i} = {{\left( {2S + 1} \right)\left( {2 - {\delta _{0,{\Lambda _i}}}} \right)} \over {\left( {2{L_{{\rm{S}}{{\rm{i}}^{\rm{ + }}}}} + 1} \right)\left( {2{S_{{\rm{S}}{{\rm{i}}^{\rm{ + }}}}} + 1} \right)\left( {2{S_{\rm{o}}} + 1} \right)}},$(4)

where δ is the Kronecker delta, S is the spin quantum number of the electronic state i, Λ is the absolute value of the projection of the electronic orbital angular momentum on the internuclear axis, and L and S are the electronic orbital angular momentum number and spin quantum number, respectively. The subscripts Si+ and О represent the ionic Si+ and atomic O, respectively. The probability pi provides a statistical explanation for the collision of Si+ (3s23p 2Pu) + O(2s22p4 3Pg). Specifically, Si+(3s23p 2Pu) + O(2s22p4 3Pg) have six and nine microstates, respectively, labeled by the spin and orbital angular momentum quantum numbers, which can generate a total of 6 × 9 = 54 molecule states for SiO+. In the radiative association of Si+ (3s23p 2Pu) + O(2s22p4 3Pg), these two atoms can approach each other along any of the 54 molecular states, that is, ∑+, Σ−, ∏, and ∆ states, each of them with total electronic spin multiplicities of doublet and quartet. 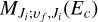MJi;υf,Ji(Ec)${M_{{J_i};{\upsilon _f},{J_i}}}\left( {{E_c}} \right)$ is the radical matrix elements, given by

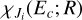MJi;υf,Ji(Ec)=∫0∞χJi(Ec;R)D(R)ψυf,Ji(R)dR,${M_{{J_i};{\upsilon _f},{J_i}}}\left( {{E_c}} \right) = \int_0^\infty {\chi {J_i}\left( {{E_c};R} \right)D\left( R \right){\psi _{\upsilon f,}}{J_i}\left( R \right){\rm{d}}R,} $(5)

where χJi(Ec;R)${\chi _{{J_i}}}\left( {{E_c};R} \right)$ is the radial wavefunction of an initial continuum state, the symbol 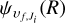ψυf,Ji(R)${\psi _{{\upsilon _f},{J_i}}}\left( R \right)$ is the radial wavefunction of a final rovibrational bound state, and D(R) is the electric TDM or PDM. The continuum and bound wavefunctions are obtained using the renormalised Numerov method (Johnson 1978, 1977).

2.3 Rate coefficients

The total rate coefficient ktot(T) of forming a bound molecule can be expressed as

ktot(T)=∑ kf←i(T),${k_{tot}}\left( T \right) = \sum {{k_{f \leftarrow i}}\left( T \right),} $(6)

where kf←i(T) represents the thermal rate coefficients for an electronic transition process ƒ ← i, and kf←i can be calculated as a function of temperature T,

         kf←i(T)=(8μπ)1/2(1kBT)3/2∫0∞Ecσf←i(Ec)exp(−EckBT)dEc,$\matrix{ {\,\,\,\,\,\,\,\,\,{k_{f \leftarrow i}}\left( T \right) = } \hfill \cr {{{\left( {{8 \over {^{\mu \pi }}}} \right)}^{1/2}}{{\left( {{1 \over {{k_{\rm{B}}}T}}} \right)}^{3/2}}\int_0^\infty {{E_c}{\sigma _{f \leftarrow i}}\left( {{E_c}} \right)\exp \left( { - {{{E_c}} \over {{k_{\rm{B}}}T}}} \right){\rm{d}}{E_c},} } \hfill \cr } $(7)

where kB is the Boltzmann constant.

thumbnail Fig. 3

Radiative association cross sections for doublet transitions (a) and quartet transitions (b) of SiO+ as a function of the collision energy.

3 Results and discussion

3.1 Radiative association cross sections

Radiative association cross sections for 18 electronic transition processes of SiO+ are obtained using the QM method, which considers the contribution of the resonance. The results for the doublet transitions and quartet transitions are shown in Fig. 3. The 2 2Π → A 2Π transition is significant over the entire range of collision energy from 0.00001 to 10 eV. For the collision energy above 1.09 eV, the 2 2Π → X 2Σ+ transition becomes as important as the 2 2Π → A 2Π transition. For the collision energy above 1.66 eV, the 2 2Σ− → A 2Π transition is also important for the SiO+ radiative association and its cross section is of the same order of magnitude as that of the 2 2Π → X 2Σ+ transition. As clearly seen in Panel a of Fig. 3, the cross sections for some transitions, such as 2 2Σ− → A 2Π, 2 2Π → X 2Σ+ and 2 2Π → 1 2∆, exhibit sharp variations, which are caused by the potential barriers on the PECs of the upper states. Other transitions including A 2Π → X 2Σ+ X 2Σ+ → A 2Π, 2 2Π → 1 2∆, 2 2Π → 1 2Σ−, 1 2Δ → A 2Π, 1 2Σ− → A 2Π and 2 2Σ− → A 2Π are relatively insignificant.

The cross sections of the quartet transitions are presented in Panel b of Fig. 3. Overall, the cross sections for the quartet transitions are smaller than that of the 2 2Π → A 2Π transition and their contribution to the total rate coefficient is expected to be insignificant. We note that the cross section for the 1 4Π → 1 4Σ+ transition decreases first with increasing energy at energies below 0.2 eV, and then increases at energies above 0.2 eV until energy of the barrier height on the 1 4Π PEC (about 2.26 eV). The variation of the cross section for the 1 4Π → 1 4Σ+ transition versus the collision energy should be reasonable. On one hand, the inner potential well for the 1 4Π state is too narrow relative to the outer one. On the other hand, the outer potential well for the 1 4Π state works at energies below the barrier height and its potential well is not significantly smaller than the potential well of the 1 4Σ+ state. The cross sections for the permanent dipole transitions of SiO+ are shown in Fig. 4. Their contributions are also small relative to the 2 2Π → A 2Π transition and are expected to contribute little to the total rate coefficient.

thumbnail Fig. 4

Radiation association cross sections as functions of the collisional energy for the permanent dipole transitions of SiO+.
thumbnail Fig. 5

Rate coefficients for doublet transitions (a), quartet transitions (b), and their total rate coefficients for the formation of SiO+.

3.2 Rate coefficients

Rate coefficients are calculated using Eq. (7) by averaging the cross sections over a Maxwellian velocity distribution over the temperature range of 10–10 000 K. Rate coefficients for doublet transitions and quartet transitions are shown in Fig. 5. The total rate coefficient for quartet transitions is smaller than that for doublet transitions over the entire temperature range. As shown in Panel a of Fig. 5, rate coefficients of the 2 2Π → X 2Σ+, 1 2Δ → A 2Σ, 1 2Σ− → A 2Π and 2 2Σ− → A 2Π transitions rise rapidly with the increase in temperature at a certain high-temperature range, corresponding to the similar trend of their cross sections.

Figure 6 presents the total rate coefficient of all the radiative association transitions, along with the rate coefficients of some important transition processes. As shown in Fig. 6, the transition process of 2 2Π → A 2Π plays a vital role in the radiative association of Si+(3s23p 2Pu) and O(2s22p4 3Pg) over the entire temperature range. Some transitions including 2 2Π → X 2Σ+, 2 2Σ− → A 2Π and 1 4Π → 1 4Σ+ are also important at high temperatures. Figure 6 also shows a comparison of the rate coefficient for the A 2Π → X 2Σ+ transition with that obtained by Andreazza et al. (1995). Differences are visible between these two sets of results and mainly result from different sources of ab initio PECs and TDM. Andreazza et al. (1995) used the PECs and TDM from Werner et al. (1982), which were calculated using the MCSCF method. We used the PECs and TDM obtained by the MRCI method from Qin et al. (2020). A comparison of these two sets of PECs and TDMs is shown in Fig. 7. PECs of the A 2Π and X 2Σ+ states show small differences, but there is a notable difference between these two sets of TDMs for the A 2Π → X 2Σ+ transition. As we all know, the MRCI method can produce more accurate TDM than the MCSCF method. Therefore, our adopted TDM of the A 2Π → X 2Σ+ transition is more reliable.

The total rate coefficient for the radiative association of SiO+ can be approximated using the three-parameter Arrhenius-Kooij function (Laidler 1996), which is expressed as

k(T)=A(T300)αe−β/T,$k\left( T \right) = A{\left( {{T \over {300}}} \right)^\alpha }{e^{ - \beta /T}},$(8)

where A, α, and ß are fitting parameters. The rate coefficient curves are divided into five temperature ranges, and the fitting parameters are summarised in Table 3. The fitted rate coefficient deviates from our calculated ones by less than 1%.

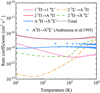thumbnail Fig. 6

Total rate coefficient and rate coefficients for some important transitions of SiO+, along with the rate coefficient for the A 2Π → X 2Σ+ transition computed by Andreazza et al. (1995). ‘Total’ denotes the total rate coefficient obtained by summing those for all transitions.

4 Conclusion

In this work, we carried out a comprehensive theoretical investigation of the radiative association for the formation of SiO+ in the collision of Si+ (3s23p 2Pu) and O(2s22p4 3Pg). We obtained the cross sections of 18 radiative association processes for SiO+ using the QM method. Our analysis of the cross sections shows that the 2 2Π → A 2Π transition is significant over the entire range of collision energy from 0.00001 to 10 eV. Other transitions including 2 2Π → X 2Σ+ and 2 2Σ− → A 2Π are also important for the SiO+ radiative association for the collision energy above 1.09 eV and 1.66 eV, respectively. The results also indicate that only considering the channels for low-lying electronic states is insufficient for accurately computing the cross sections. The calculation of A 2Π → X 2Σ+ underestimates the total cross section by more than one order of magnitude.

The rate coefficients of 18 electronic transition channels for the formation of SiO+ are then computed for temperatures from 10 to 10 000 K and compared with those computed by Andreazza et al. (1995), who only considered the A 2Π → X 2Σ+ transition channel. The magnitude of the rate coefficients for the A 2Π → X 2Σ+ transition computed by Andreazza et al. (1995) is about 10−19 cm3 s−1, which is about an order of magnitude larger than ours. However, the PECs and TDM adopted by Andreazza et al. (1995) are obtained using the MCSCF method, which is not as precise as the MRCI method used here. Moreover, we also considered other possible radiative association channels for the formation of SiO+. The obtained total rate coefficient decreases at first and then increases with the increase of temperatures from 10 to 10 000 K, and its minimum value is about 7.72 × 10−18 cm3 s−1 at 458 K, which is higher than most other radiative association reactions with atoms or atomic ions in the ground state, such as CN (Zhang et al. 2022), BeH+, and BeD+ (Szabo et al. 2021). In addition, we computed the rate coefficients for temperatures from 10 to 300 K, which were not considered by Andreazza et al. (1995).

As a formation mechanism of SiO+, the rate coefficient for the radiative association of Si+(3s23p 2Pu) and O(2s22p4 3Pg) from Andreazza et al. (1995) was included the UMIST Database for Astrochemistry (UDfA; McElroy et al. 2013). Moreover, this rate coefficient from Andreazza et al. (1995) was used in two practical examples in astrochemistry modelling. One is the study of the formation and destruction of molecules in the ejecta of Population III SNe from Cherchneff & Dwek (2009), who used a chemical kinetic approach to follow the evolution of molecular abundances from day 100 to day 1000 after explosion and pointed out that radiative association reactions could carry off the excess energy released in the formation of the adduct. In the other example, Liljegren et al. (2022) modelled the molecular chemistry of Type Ibc SNe, coupling a chemical kinetic network including carbon, oxygen, silicon, and sulfur-bearing molecules into the non-local thermodynamic equilibrium (NLTE) spectral synthesis code small ubiquitin-related modifier (SUMO), in which radiative association of Si+ and O was included. Hence, the rate coefficient for the title reaction is important in astro-chemistry modelling. Our work provides an improvement of this rate coefficient.

In future work, it would be worth considering the cross sections for the formation of SiO+ at energies lying above the Si(3Pg) and O+(4Su) dissociation limit, which is about 5.47 eV relative to the Si+(2Pu) and O(3Pg) dissociation limit. At that energy, the channel for the charge transfer,

Si+(2Pu)+O(3Pg)→Si(3Pg)+O+(4Su),${\rm{S}}{{\rm{i}}^ + }\left( {^2{{\rm{P}}_{\rm{u}}}} \right) + {\rm{O}}\left( {^3{{\rm{P}}_{\rm{g}}}} \right) \to {\rm{Si}}\left( {^3{{\rm{P}}_{\rm{g}}}} \right) + {{\rm{O}}^ + }\left( {^4{{\rm{S}}_{\rm{u}}}} \right),$(9)

would probably open and compete with the radiative association. There have been no reports on the cross section and rate of the reaction (9). When computing the cross section of the channel (9), Eq. (5) in Sect. 2.2 is also needed, but its wavefunction for the bound state ψ in Eq. (5) should be replaced by the wavefunction for the corresponding continuum state χ. Such calculations would be interesting and useful for a complete understanding of the collision between Si+ and O in their ground states.

thumbnail Fig. 7

Comparison of the potential energy curves for the A 2Π and X 2Σ+ states (a) and transition dipole moment for the A 2Π → X 2Σ+ transition (b) calculated by Qin et al. (2020) using the icMRCI method with those computed by Werner et al. (1982) using the MCSCF method.
Table 3

Fitting parameters according to Kooij function [equation (8)] for the total rate coefficient.

Acknowledgements

This work is sponsored by National Natural Science Foundation of China (52106098), Natural Science Foundation of Shandong Province (ZR2021QE021), China Postdoctoral Science Foundation (2021M701977), Postdoctoral Innovation Project of Shandong Province and Postdoctoral Applied Research Project of Qingdao City. The scientific calculations in this paper have been done on the HPC Cloud Platform of Shandong University.

References

  1. Andreazza, C., & de Almeida, A. 2014, MNRAS, 437, 2932 [NASA ADS] [CrossRef] [Google Scholar]
  2. Andreazza, C., Singh, P.D., & Sanzovo, G. 1995, ApJ, 451, 889 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andreazza, C., Singh, P., & Sanzovo, G. 1997, ApJ, 475, 853 [NASA ADS] [CrossRef] [Google Scholar]
  4. Andreazza, C., de Almeida, A., Vichietti, R., & Ceccatto, D. 2012, MNRAS, 427, 833 [NASA ADS] [CrossRef] [Google Scholar]
  5. Andreazza, C., de Almeida, A., & Borin, A.C. 2016, MNRAS, 457, 3096 [NASA ADS] [CrossRef] [Google Scholar]
  6. Antipov, S.V., Sjölander, T., Nyman, G., & Gustafsson, M. 2009, J. Chem. Phys., 131, 074302 [NASA ADS] [CrossRef] [Google Scholar]
  7. Babb, J.F., & McLaughlin, B.M. 2017, MNRAS, 468, 2052 [CrossRef] [Google Scholar]
  8. Babb, J.F., Smyth, R.T., & McLaughlin, B. 2019, ApJ, 876, 38 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bai, T., Qin, Z., & Liu, L. 2021, MNRAS, 500, 2496 [Google Scholar]
  10. Bai, T., Qin, Z., & Liu, L. 2022, MNRAS, 510, 1649 [Google Scholar]
  11. Bain, R., & Bardsley, J. 1972, J. Phys. B Atom. Mol. Phys., 5, 277 [CrossRef] [Google Scholar]
  12. Barinovs, Ğ., & van Hemert, M.C. 2006, ApJ, 636, 923 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bates, D. 1951, Proc. Phys. Soc. B, 64, 805 [NASA ADS] [CrossRef] [Google Scholar]
  14. Breit, G., & Wigner, E. 1936, Phys. Rev., 49, 519 [CrossRef] [Google Scholar]
  15. Brugamyer, E., Dodson-Robinson, S.E., Cochran, W.D., & Sneden, C. 2011, ApJ, 738, 97 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cai, Z.-L., & François, J. 1999, J. Mol. Spectrosc., 197, 12 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chattopadhyaya, S., Chattopadhyay, A., & Das, K.K. 2003, J. Mol. Struct. Theochem, 639, 177 [CrossRef] [Google Scholar]
  18. Cherchneff, I., & Dwek, E. 2009, ApJ, 703, 642 [NASA ADS] [CrossRef] [Google Scholar]
  19. Clegg, R., Van Ijzendoorn, L., & Allamandola, L. 1983, MNRAS, 203, 125 [NASA ADS] [CrossRef] [Google Scholar]
  20. Forrey, R.C. 2015, J. Chem. Phys., 143, 024101 [NASA ADS] [CrossRef] [Google Scholar]
  21. Forrey, R., Babb, J., Stancil, P., & McLaughlin, B. 2018, MNRAS, 479, 4727 [NASA ADS] [CrossRef] [Google Scholar]
  22. Franz, J., Gustafsson, M., & Nyman, G. 2011, MNRAS, 414, 3547 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gerlich, D., & Horning, S. 1992, Chem. Rev., 92, 1509 [CrossRef] [Google Scholar]
  24. Glassgold, A., Lucas, R., & Omont, A. 1986, A&A, 157, 35 [NASA ADS] [Google Scholar]
  25. Golubev, N.V., Bezrukov, D.S., Gustafsson, M., Nyman, G., & Antipov, S.V. 2013, J. Phys. Chem. A, 117, 8184 [NASA ADS] [CrossRef] [Google Scholar]
  26. Grebowsky, J.M., & Aikin, A.C. 2002, In Situ Measurements of Meteoric Ions, Meteors in the Earth’s Atmosphere (Cambridge: Cambridge University Press), 189 [Google Scholar]
  27. Gustafsson, M. 2013, J. Chem. Phys., 138, 074308 [NASA ADS] [CrossRef] [Google Scholar]
  28. Gustafsson, M. 2020, J. Chem. Phys., 153, 114305 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gustafsson, M., & Forrey, R.C. 2019, J. Chem. Phys., 150, 224301 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gustafsson, M., Monge-Palacios, M., & Nyman, G. 2014, J. Chem. Phys., 140, 184301 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hansson, A., & Watson, J.K. 2005, J. Mol. Spectrosc., 233, 169 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hervig, M.E., Deaver, L.E., Bardeen, C.G., et al. 2012, J. Atmos. Sol. Terr. Phys., 84, 1 [CrossRef] [Google Scholar]
  33. Johnson, B.R. 1977, J. Chem. Phys., 67, 4086 [Google Scholar]
  34. Johnson, B.R. 1978, J. Chem. Phys., 69, 4678 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kathir, R., Nyman, G., & Gustafsson, M. 2017, MNRAS, 470, 3068 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kopp, E., Balsiger, F., & Murad, E. 1995, Geophys. Res. Lett., 22, 3473 [NASA ADS] [CrossRef] [Google Scholar]
  37. Laidler, K.J. 1996, Pure Appl. Chem., 68, 149 [Google Scholar]
  38. Langer, W.D., & Glassgold, A. 1990, ApJ, 352, 123 [NASA ADS] [CrossRef] [Google Scholar]
  39. Liljegren, S., Jerkstrand, A., Barklem, P., et al. 2022, A&A, submitted, [arXiv:2203.07021] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Liu, C., Qu, Y., Wang, J., Li, Y., & Buenker, R. 2009, Phys. Lett. A., 373, 3761 [NASA ADS] [CrossRef] [Google Scholar]
  41. Liu, X., Qu, Y., Xiao, B., et al. 2010, Phys. Rev. A., 81, 022717 [Google Scholar]
  42. McElroy, D., Walsh, C., Markwick, A., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Meng, H., Qin, Z., & Liu, L. 2022, ApJ, 935, 148 [NASA ADS] [CrossRef] [Google Scholar]
  44. Mies, F.H. 1969, J. Chem. Phys., 51, 787 [NASA ADS] [CrossRef] [Google Scholar]
  45. Neufeld, D.A., & Dalgarno, A. 1989, ApJ, 344, 251 [NASA ADS] [CrossRef] [Google Scholar]
  46. Nyman, G., Gustafsson, M., & Antipov, S.V. 2015, Int. Rev. Phys. Chem., 34, 385 [CrossRef] [Google Scholar]
  47. Öström, J., Bezrukov, D.S., Nyman, G., & Gustafsson, M. 2016, J. Chem. Phys., 144, 044302 [CrossRef] [Google Scholar]
  48. Plane, J.M., Gómez-Martín, J.C., Feng, W., & Janches, D. 2016, J. Geophys. Res. Atmos., 121, 3718 [NASA ADS] [CrossRef] [Google Scholar]
  49. Qin, Z., Bai, T., Zhao, J., & Liu, L. 2020, J. Mol. Spectrosc., 370, 111298 [NASA ADS] [CrossRef] [Google Scholar]
  50. Qin, Z., Bai, T., & Liu, L. 2021, MNRAS, 507, 2930 [NASA ADS] [CrossRef] [Google Scholar]
  51. Rubin, R.H., Dufour, R.J., & Walter, D.K. 1993, ApJ, 413, 242 [NASA ADS] [CrossRef] [Google Scholar]
  52. Scalo, J., & Slavsky, D. 1980, ApJ, 239, L73 [NASA ADS] [CrossRef] [Google Scholar]
  53. Shi, D., Li, W., Xing, W., et al. 2012, Comput. Theor. Chem., 980, 73 [CrossRef] [Google Scholar]
  54. Šimsová-Zámecníková, M., Soldán, P., & Gustafsson, M. 2022, A&A, 664, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Singh, M., Bredohl, H., Remy, F., & Dubois, I. 1973, J. Phys. B Atom. Mol. Phys., 6, 2656 [CrossRef] [Google Scholar]
  56. Stancil, P., Kirby, K., Gu, J.-P., et al. 2000, A&AS, 142, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Szabó, P., & Gustafsson, M. 2017, J. Chem. Phys., 147, 094308 [CrossRef] [Google Scholar]
  58. Szabó, P., & Gustafsson, M. 2019, MNRAS, 483, 3574 [Google Scholar]
  59. Szabo, P., Goger, S., & Gustafsson, M. 2021, Front. Astron. Space Sci., 8, 704953 [CrossRef] [Google Scholar]
  60. Takano, S., Saito, S., & Tsuji, T. 1992, PASJ, 44, 469 [NASA ADS] [Google Scholar]
  61. Turner, J., & Dalgarno, A. 1977, ApJ, 213, 386 [NASA ADS] [CrossRef] [Google Scholar]
  62. Walmsley, C., Pineau des Forêts, G., & Flower, D. 1999, A&A, 342, 542 [NASA ADS] [Google Scholar]
  63. Watson, J.K. 2008, J. Mol. Spectrosc., 252, 5 [NASA ADS] [CrossRef] [Google Scholar]
  64. Werner, H.-J., Rosmus, P., & Grimm, M. 1982, Chem. Phys., 73, 169 [NASA ADS] [CrossRef] [Google Scholar]
  65. Zámecníková, M., Gustafsson, M., Nyman, G., & Soldán, P. 2020, MNRAS, 492, 3794 [CrossRef] [Google Scholar]
  66. Zhang, S., Qin, Z., & Liu, L. 2022, MNRAS, 515, 6066 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Local maximums at the PECs of the 2 2Π, 2 2Σ−, and 1 4Π states.

In the text
Table 2

Radiative association processes studied in this work for SiO+.

In the text
Table 3

Fitting parameters according to Kooij function [equation (8)] for the total rate coefficient.

In the text

All Figures

thumbnail Fig. 1

Potential energy curves (a) and transition dipole moments (b) for SiO+ which are taken from Qin et al. (2020).
In the text
thumbnail Fig. 2

Permanent dipole moments for the electronic states of SiO+ computed in this work.
In the text
thumbnail Fig. 3

Radiative association cross sections for doublet transitions (a) and quartet transitions (b) of SiO+ as a function of the collision energy.
In the text
thumbnail Fig. 4

Radiation association cross sections as functions of the collisional energy for the permanent dipole transitions of SiO+.
In the text
thumbnail Fig. 5

Rate coefficients for doublet transitions (a), quartet transitions (b), and their total rate coefficients for the formation of SiO+.
In the text
thumbnail Fig. 6

Total rate coefficient and rate coefficients for some important transitions of SiO+, along with the rate coefficient for the A 2Π → X 2Σ+ transition computed by Andreazza et al. (1995). ‘Total’ denotes the total rate coefficient obtained by summing those for all transitions.
In the text
thumbnail Fig. 7

Comparison of the potential energy curves for the A 2Π and X 2Σ+ states (a) and transition dipole moment for the A 2Π → X 2Σ+ transition (b) calculated by Qin et al. (2020) using the icMRCI method with those computed by Werner et al. (1982) using the MCSCF method.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.