| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 3 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202244496 | |
| Published online | 04 November 2022 | |
Satellite shadows through stellar occultations
1
Department of Astrophysics/IMAPP, Radboud University,
PO Box 9010,
6500 GL
Nijmegen, The Netherlands
e-mail: p.groot@astro.ru.nl
3
South African Astronomical Observatory,
PO Box 9,
Observatory,
7935
Cape Town, South Africa
3
Department of Astronomy, University of Cape Town,
Private Bag X3,
Rondebosch
7701, South Africa
Received:
14
July
2022
Accepted:
7
September
2022
Aims. The impact of mega-constellations of satellites in low-Earth orbit during nighttime optical observations is assessed.
Methods. Orbital geometry is used to calculate the impact of stellar occultations by satellites on the photometry of individual stars as well as the effect on the photometric calibration of wide-field observations.
Results. Starlink-type satellites will have occultation disks several arcseconds across. Together with occultation crossing times of 0.1−100 ms, this will lead to photometric ‘jitter’ on the flux determination of stars. The level of impact for a given star depends on the ratio of the integration time of the frame over the occultation crossing time. In current-day CCD-based synoptic surveys, this impact is negligible (≪1%), but with future CMOS-based wide-field surveys obtaining data at frequencies >1 Hz, the impact will grow towards complete dropouts. At integration times similar to the occultation crossing time, the orbit of a satellite can be traced using the occultation method. At even shorter integration times, the shape of the occulting satellite can be deduced.
Conclusions. Stellar occultations by passing satellites, enabled by high-speed CMOS technology, will be a new method for studying orbiting satellites. Large-scale monitoring programs will be needed to independently determine and update the orbits of satellites.
Key words: methods: observational / space vehicles / surveys / occultations
© P. J. Groot 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
As mega-constellations of man-made satellites are being launched, their impact on astronomy needs to be assessed. The aspect of pollution in the optical and radio bands has been greatly emphasised (e.g. Witze 2019; Gallozzi et al. 2020). In the optical, this pollution is mostly restricted to the twilight hours of the night when the satellites still catch sunlight while night has already descended on the ground-based telescopes (see e.g. Bassa et al. 2022; Mróz et al. 2022; Tregloan-Reed et al. 2021; Mallama 2021; Tyson et al. 2020; Hainaut & Williams 2020; McDowell 2020). However, the effect of satellite constellations on optical ground-based observations is not limited to the twilight hours. During the night, satellites will cause occultations of stars located along their path. As both the occulter (the satellite) and the occulted object (the star) are above the Earth’s atmosphere, the occultation will be complete as the angular diameter of the satellite (θs) will be much larger than that of the background star (θ⋆).
In Sect. 2, we revisit the basic geometries involved. In Sect. 3, we overview various current and upcoming satellite constellations. In Sect. 4, we apply the analysis to a number of satellite types, and in Sect. 5 we revisit the question on how feasible it is to discover and characterise satellites through optical observations of stellar occultations.
2 Geometry
Throughout this exercise we make two simplifying assumptions. First, we assume a satellite has a circular shape as seen from any observatory on Earth, characterised by a satellite radius, Rs, over which area the satellite is completely opaque. Secondly, we assume the path of the satellite to be on a great circle passing through the zenith.
The assumed geometry is that of a satellite circling the Earth (with radius, R⊕, taken as 6378 km) at an orbital altitude h. With an Earth mass, M⊕, taken as 5.976 × 1024 kg, the orbital period, P, follows from Kepler’s laws as
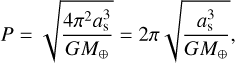 (1)
(1)
with as = R⊕ + h, the radius of the satellite’s orbit from the centre of the Earth, and G Newton’s gravitational constant.
The tangential velocity of a satellite passing overhead, ignoring the Earth’s rotation, is given by
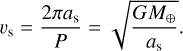 (2)
(2)
The satellite will produce an occultation disk (θs) with an angular diameter of
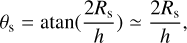 (3)
(3)
where the approximation is justified for the small angles involved. The angular diameter of a satellite is, in all practical cases, much larger than the angular diameter (θ⋆) of a background star (θ⋆ << 10 mas). The occultation will therefore be complete, and the duration is set by the rate of motion of the satellite. To first order, the crossing time, τs, is the time it takes the satellite to move its own size as it passes through the zenith, that is,
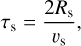 (4)
(4)
where vs is the orbital velocity of the satellite. It is the crossing time, τs, that needs to be compared to the typical integration time in synoptic surveys to assess the impact of a stellar occultation by a satellite.
The size of the satellite’s shadow on Earth is equal to the size of the satellite, as stars can be taken to be infinitely far away. Hence, if the aperture, D, of the telescope is larger than the size of the satellite (D > 2 Rs), the occultation will not be total and the ingress and egress duration of the occultation will be flattened. This sets an upper limit to the size of the telescope used if one aims to detect a total occultation.
3 Shadows by satellite constellations
Most satellites can be grouped into a small number of orbits: low-Earth orbit (LEO), at altitudes h = 350–500 km; the global positioning system (GPS) medium-Earth orbit (MEO) belt at h ~ 20 000 km; and geostationary (GEO) satellites at h = 36 000 km. The sizes of satellites vary strongly, from CubeSats with Rs ~ 0.5 m, to Starlink-type satellites with Rs ~ 5 m, to larger, but rarer, satellites such as the KeyHole Hubble-type satellites with Rs ~ 15 m and the Orion/Mentor radio dishes (Rs ~ 100 m) in GEO orbits.
In Table 1, we list the relevant occultation disks and crossing times for the categories listed above. Figure 1 shows the crossing times as a function of orbital altitude and size of the satellite. Figure 1 shows that, for feasible satellite sizes, the crossing times are generally ≲ 100 ms. Although this appears low, we highlight the impact of this in Sect. 4.
4 Impact on ground-based astronomy
Mega-constellations of satellites are of major concern to ground-based astronomy. With more than 40 000 satellites planned to be launched over the next few years, ground-based astronomy will face the situation that there will be one to several satellites at any moment per square degree of sky (see e.g. Bassa et al. 2022). Major synoptic surveys with instantaneous fields-of-view, Ω > 1 square degree, will have multiple to tens of satellites crossing each image (Mróz et al. 2022). The effect on nighttime ground-based photometry will be that occulted stars will be completely blocked out for a crossing time, τs. The effect on the resulting photometry depends on the ratio of the crossing time over the integration time, tnt, of an exposure: f = tint/τs. The impact depends on whether this ratio, f, is larger or smaller than unity.
4.1 Long integration times: f > 1
Most current ground-based synoptic surveys use integration times tint > 1 s. The effect of a satellite shadow passing through the field-of-view is therefore that of an occulting trail that blocks part of the integrated light of stars located along its path with a width θs. The fractional decrease in the light of any given star is equal to 1/f, assuming the occultation to be complete for the crossing time, τs, which also depends on the ratio 2 Rs/D.
For a Starlink-type satellite, the ratio f is ~12 000 for a Vera Rubin Observatory exposure time of 15 s (LSST Science Collaboration et al. 2017), ~23 000 for Zwicky Transient Facility integration times of 30s (Bellm et al. 2019), and ~46 000 for BlackGEM exposure times of 60 s (Bloemen et al. 2016). As the absolute photometric precision in ground-based astronomy rarely exceeds the 1% level, such drops in the light curve may not be noticeable as of yet.
The area affected, fΩ, by a worst-case crossing (corner to corner) is about 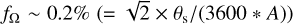 for a wide-field imager with an A × A square degrees field-of-view. In some parts of the Galactic plane and bulge, the ground-based, discernible stellar densities reach >500 000 per square degree down to g ~ 20 mag (Drew et al. 2014; Groot et al. 2009), and therefore hundreds of stars will lie in the path of occultation.
for a wide-field imager with an A × A square degrees field-of-view. In some parts of the Galactic plane and bulge, the ground-based, discernible stellar densities reach >500 000 per square degree down to g ~ 20 mag (Drew et al. 2014; Groot et al. 2009), and therefore hundreds of stars will lie in the path of occultation.
A secondary effect is introduced by the absolute photometric calibration of a single frame. Generally, this is achieved by measuring the flux of a number of calibrator stars across the field-of-view and taking the ratio of the measured flux with the tabulated brightness of these stars. This is currently done using Gaia Data Release 2 or 3 (DR2 or DR3) photometry for the calibrator stars. As a satellite shadow crosses the field-of-view during an integration, the measured brightness of the calibrator stars that lie on the path of the satellite will be lower than expected, and therefore the photometric calibration of the whole frame will be affected, artificially ‘brightening’ the whole frame: as the calibrators are fainter than expected, this will result in an artificial increase in the apparent brightness of all other stars in the frame. In current-day surveys, this will not be a major problem as the calibrator dimming will be equal to the ratio of the number of affected (calibrator) stars over the total number of (calibrator) stars in the image. For a 1° × 1° field-of-view and a single Starlink-type satellite, the occulted area is, at worst, 0.2% of the total area (7.2 square arcminutes), and therefore, assuming a uniform stellar density, also only 0.2% of stars are affected, at a level of 1/f per star, so the total impact on the photometric calibration is negligible.
We note that the total crossing time, tcross, of a Starlink-type satellite over a 1-degree field-of-view is equal to tcross = A/θsrs = 0.9 s. To demonstrate these satellite shadows, the best current-day option would be to observe GEO satellites that will cause a trail of 1 arcmin for a 60 s exposure.
Overview of orbital altitudes (h), sizes (Rs), angular diameters (θs), speeds (ωs), and crossing times (τs) of satellite categories.
 |
Fig. 1 Shadow crossing time as a function of orbital altitude of a satellite around Earth, for various satellite sizes. Indicated are representative classes of satellites in LEO, MEO, and GEO orbits. |
4.2 Short integration times: f ≲ 1
CMOS-camera technology is rapidly advancing. CMOS cameras with frame sizes exceeding 6000 × 6000 pixels and quantum efficiencies >90% are available. The expectation is therefore that within a few years CMOS technology will completely replace current-day CCD technology in ground-based astronomy (e.g. Niino et al. 2022; Zhang et al. 2020). With this comes the possibility to take much shorter exposures thanks to the parallel read-out technology in CMOS cameras. Integration times shorter than 1s become feasible. As can be seen in Table 1 and Fig. 1, the 1% influence on any given star in absolute photometry becomes relevant for integration times shorter than 0.1s for Starlink-type satellites, and shorter than 6 s for an Orion-type satellite.
Full-frame read-out speeds on large-format CMOS cameras are currently in the 24 Hz range. Therefore, ‘SuperHertz’ wide-field cameras will appear, coupled to large-aperture telescopes (e.g. Sako et al. 2018; Niino et al. 2022).
At 24 Hz, the integration times come in the range of the crossing times given in Table 1. With 2 × 2 binning, speeds up to 100 Hz can be achieved, and a 10% dimming effect can be expected for Starlink-type satellites. With further binning or windowing, crossing times can be resolved in time, and the path of a satellite can be followed by a series of ‘dropouts’ of stars along the orbit. This will allow for orbit determinations of satellites larger than a few metres, depending on their orbital altitudes.
Additionally, the assumption of a circular, fully opaque occultation patch can be relaxed. Set against a sufficiently dense stellar field, the shape of each satellite can be deduced from the complex light curve that will be produced as the satellite path is followed across the sky. With Gaia (Early) DR3 astrometric precision (σ) on the location of each star at a level of 1 mas (Lindegren et al. 2021), the ratio σ/θs ≪ f, and therefore it will be the integration time, tint, that is the limiting factor on the level of detail that will be retrievable. Conceptually, the level of detail will be of the order of f Rs.
For satellites in known orbits CMOS cameras can be sub-arrayed to allow for read-out speeds of ~1000 Hz, leading to smaller f. A detailed modelling is outside the scope of this study, but can easily be conceptualised. This method will allow for the determination of the position and shape of a satellite at accuracies <1 m when f reaches 0.1 or less.
The effect noted in Sect. 4.1 on the photometric calibration of the full frame will disappear when f < 1. Although the effect on each individual star will become stronger as fapproaches unity, the length of a trail through each exposure will become shorter and shorter, and fΩ will approach zero.
5 Outlook and discussion
Mega-constellations in LEO will have a significant impact on ground-based astronomy, in particular for wide-field synoptic surveys. During twilight hours the reflected sunlight will cause bright streaks in the images. We have shown that during hours of darkness, satellites will cause a shadow path by blocking out the light of background stars through occultations.
For current-day longer-duration exposures (tint > 1 s), the effect is modest and restricted to downwards photometric jitter on individual stars. However, with CMOS technology advancing quickly, integration times similar to the satellite’s crossing time over any given star come within reach. This will lead to strong dropouts on an individual star’s light curve. It also opens up the possibility to use the occultation trail to detect and track the satellite in its orbit across the sky. This effect is completely independent from the albedo or ‘stealth’ capabilities of the satellite, and also extends beyond just the optical wavelength regime.
With integration times shorter than the occultation crossing time, and set against sufficiently crowded stellar fields (e.g. the Galactic plane and bulge, or the Magellanic Clouds), the shape of satellites will be deducible, opening up a completely new way to characterise satellites in orbit.
Acknowledgements
P.J.G. is partially supported by NRF SARChI grant 111692. The author thanks Frank Verbunt for an insightful discussion, and David Palmer for pointing out a conceptual mistake in a previous version and making useful suggestions for simplifications.
References
- Bassa, C. G., Hainaut, O. R., & Galadí-Enríquez, D. 2022, A&A, 657, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellm, E. C., Kulkarni, S. R., Barlow, T., et al. 2019, PASP, 131, 068003 [Google Scholar]
- Bloemen, S., Groot, P., Woudt, P., et al. 2016, SPIE Conf. Ser., 9906, 990664 [NASA ADS] [Google Scholar]
- Drew, J. E., Gonzalez-Solares, E., Greimel, R., et al. 2014, MNRAS, 440, 2036 [Google Scholar]
- Gallozzi, S., Paris, D., Scardia, M., & Dubois, D. 2020, ArXiv e-prints, [arXiv:2003.05472] [Google Scholar]
- Groot, P. J., Verbeek, K., Greimel, R., et al. 2009, MNRAS, 399, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hainaut, O. R., & Williams, A. P. 2020, A&A, 636, A121 [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- LSST Science Collaboration (Marshall, P., et al.) 2017, ArXiv e-prints, [arXiv:1708.04058] [Google Scholar]
- Mallama, A. 2021, ArXiv e-prints, [arXiv:2101.00374] [Google Scholar]
- McDowell, J. C. 2020, ApJ, 892, L36 [Google Scholar]
- Mróz, P., Otarola, A., Prince, T. A., et al. 2022, ApJ, 924, L30 [CrossRef] [Google Scholar]
- Niino, Y., Doi, M., Sako, S., et al. 2022, ApJ, 931, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, S., Ohsawa, R., Takahashi, H., et al. 2018, SPIE Conf. Ser., 10702, 107020J [NASA ADS] [Google Scholar]
- Tregloan-Reed, J., Otarola, A., Unda-Sanzana, E., et al. 2021, A&A, 647, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tyson, J. A., Ivezić, Ž., Bradshaw, A., et al. 2020, AJ, 160, 226 [Google Scholar]
- Witze, A. 2019, Nature, 575, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-H., Zhang, H.-F., Qu, W.-Q., et al. 2020, SPIE Conf. Ser., 11454, 1145407 [NASA ADS] [Google Scholar]
All Tables
Overview of orbital altitudes (h), sizes (Rs), angular diameters (θs), speeds (ωs), and crossing times (τs) of satellite categories.
All Figures
 |
Fig. 1 Shadow crossing time as a function of orbital altitude of a satellite around Earth, for various satellite sizes. Indicated are representative classes of satellites in LEO, MEO, and GEO orbits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


