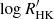EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 664 (August 2022) A&A, 664 (2022) L9 Full HTML
Open Access
Issue
A&A
Volume 664, August 2022
Article Number L9
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202244385
Published online 17 August 2022

© A. Mohan et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

In recent years, there has been a growing interest in the atmospheric activity of cool main-sequence stars (cool stars; effective temperature, Teff ∼ 3000–7000 K) especially due to the links between activity, exo-space weather, and exo-planet habitability (e.g., Grießmeier et al. 2005; Vidotto et al. 2013; Moschou et al. 2019; Odert et al. 2020). Cool stars of spectral types F – M together host the largest number of Earth-like exoplanets in habitable zones (Bashi et al. 2020). However, owing to their outer convection layer, these stars have active atmospheres that drive flares, eruptions, and other high-energy phenomena, which can potentially affect the atmospheres of nearby planets in habitable zones (Lammer et al. 2007; Zendejas et al. 2010). Ground- and space-based instruments provide plenty of data on stellar atmospheric emission primarily in X-ray to optical wavebands, owing to large dedicated surveys (e.g., Perryman et al. 1997; De Pascale et al. 2014; Gaia Collaboration 2021). Based on the X-ray to optical observables, which are sensitive to different stellar atmospheric phenomena and layers, different activity indicators have been constructed. Commonly used indicators include the ratio of the Ca II H-K flux to bolometric flux (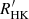, Noyes et al. (1984)) and the X-ray to bolometric flux ratio (RX). These activity indicators show trends with several physical parameters such as Teff, the rotation period, magnetic field strength, metallicity, among others, sometimes with complex multi-dimensional dependencies (e.g., Noyes et al. 1984; Stepien 1994; Marsden et al. 2014; Vidotto et al. 2014). Though these trends provide a qualitative physical picture of the physical dependencies of activity, the large value ranges of these indicators make it hard to derive robust quantitative relations. For instance, Pace (2013) showed an age-dependent bimodality of 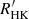values for cool stars of same Teff. Even the values for a single star varied by factors of 2 − 4, making it hard to distinguish the cool stars (Teff ∼ 4000–7000 K) along the 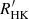axis. Similar studies on RX values have revealed variations as large as an order of magnitude in Sun-like stars (e.g., Micela & Marino 2003). These studies show that the common indicators cannot provide robust quantitative scales which are essential to better constrain the atmospheric physical models and gain physical insights on the emergence of different levels of activity in stars of different types.

Observations and related models suggest that the atmospheric structure of cool stars undergoes significant changes as function of spectral type or equivalently in the Teff range 3000–7000 K (e.g., Donati & Landstreet 2009; Linsky 2017). Being the middle layer of the stellar atmosphere, chromosphere plays a crucial role in the generation and propagation of active phenomena across the stellar atmosphere (for a review, see Linsky 2017). It is hence highly desirable to construct a new and more reliable observational indicator of the chromospheric structure of cool stars, which is closely linked to the observed activity. Continuum emission in the millimetre (mm) range (∼30–1000 GHz) originates at different heights in the stellar chromosphere primarily due to thermal bremsstrahlung, which is formed under local thermal equilibrium (LTE) conditions (Wedemeyer et al. 2016). Owing to its high sensitivity, ALMA enables the detection of chromospheric mm emission for a larger number of potential stellar targets than possible before. Several recent solar and stellar mm observations have demonstrated the unique tomographic potential of the mm-brightness temperature spectrum (mm-TB(ν)) to facilitate the deduction of the chromospheric thermal structure and dynamics at various atmospheric layers in cool stars (e.g., White et al. 2017, 2020; Trigilio et al. 2018). In the previous paper in this series (Paper I; Mohan et al. 2021), the mm-TB(ν) spectrum was derived for main-sequence stars using archival ALMA data. The sample was made by systematically avoiding stars with potential flux contamination from known debris disks or unresolved companion stars. Assuming that the observed stellar mm flux can be approximated with a LTE Rayleigh-Jeans spectrum, TB(ν) is expected to reflect the atmospheric thermal stratification. The mm-TB(ν) of every cool star in the sample significantly deviated from a corresponding purely photospheric model (PHOENIX; Hauschildt & Baron 1999) spectrum, with the deviation from the photospheric model increasing as ν decreased (Fig. 1). The rise of TB with decreasing ν is consistent with probing hotter chromospheric layers at higher heights, indicating the existence of a chromosphere and, with that, the presence of chromospheric heating and potentially higher activity (Paper I). In this paper, we fit the compiled mm-TB(ν) for every star and explore the relationships between spectral structure and stellar physical properties, particularly focussing on the cool stars in the sample.

thumbnail Fig. 1.

mm-TB(ν) in the 30–1000 GHz range. Titles show the names and spectral types. Family of power-law functions consistent with the αmm estimation errors (shaded regions) and photospheric models (dotted line) are shown. For the Sun, chromospheric FAL models are shown. Multi-epoch data at ν are coloured differently.

In Sect. 2, the data and analysis methodology are described. The results are presented in Sect. 3, and a discussion in Sect. 4 is followed by our conclusions and outlook in Sect. 5.

2. Data and methodology

The mm-TB(ν) data used for this work are part of the sample of main-sequence stars presented in Paper I. Here, we selected only those stars in the sample with more than one data point in the mm/sub-mm range (30–1000 GHz). The resultant sub-sample of nine stars covers a Teff range of ∼ 5000–100 000 K (A – K type). Though the original sample compiled data in the 10–1000 GHz range, we chose to stick to the mm/sub-mm range for two reasons. Firstly, for cool stars, the assumption of LTE emission is believed to be generally valid beyond 30 GHz. For the Sun, this assumption is confirmed by detailed 3D atmospheric model calculations (see Wedemeyer et al. 2016, and references therein). For the other cool stars in our sample, the LTE nature of the mm emission has been demonstrated via data-driven modelling studies using scaled 1D solar models (Vernazza et al. 1981) or solar-like models (Tapia-Vázquez & De la Luz 2020). Trigilio et al. (2018) carried out this exercise for the α Cen system (G and K dwarf) and White et al. (2020) did so for the F dwarfs. However, below 30 GHz, non-thermal emission from the corona can be relevant as shown for ϵ Eri by Suresh et al. (2020). Secondly, the data below 30 GHz are either very sparse or non-existent for the stars in our sample.

For the α Cen binary, there exist multiple ALMA observations at certain frequencies gathered years apart and hence revealing the inherent time variability in the emission. Similarly ϵ Eri observations at different frequencies were made years apart (Suresh et al. 2020). The solar data at 34 GHz come from periods of minimum and maximum activity during solar cycle 23 (White 2004). So, the mm-TB(ν) of these stars represent emission averaged over the respective activity cycle timescales.

3. Results

Figure 1 shows a collage of TB(ν) for the cool stars in our sub-sample along with an A-type star for comparison. The years during which data were collected are given in the legends along with the corresponding radio telescopes. Multi-epoch observations at the same frequency are shown in different colours. The dotted line shows the photospheric emission model. For the Sun, quiet chromospheric spectra based on FAL A and C models (Loukitcheva et al. 2004) are shown, revealing the chromospheric origin of the observed TB(ν). The observed TB(ν) of every star was fitted by a power law (TB(ν) ∝ ναmm). The shaded region in each subplot shows the family of curves consistent within the error range of the χ2 fit. The errors on αmm could not be estimated for γ Vir A and B since there are only two TB data points. While deriving αmm for the α Cen system and the Sun, we used mean TB values at frequencies for which multi-epoch data existed. A systematic error was added to the mean TB to account for emission variability. Despite the emission variability in the multi-epoch data, αmm values are quite robust with relatively low-error ranges, letting us explore its physical dependencies.

Figure 2 explores αmm vs. various physical parameters. The sample consists of both an old and young group of stars with ages either above or below 1 Gyr, respectively. The plot shows the old group in bigger markers, revealing the physical dependencies of αmm, modelled by power-law functions (red curves) with the index, β. There is only one cool star in the young group, ϵ Eri. The A-type stars αPsA and α CMa show a negative αmm, as they lack hotter upper atmospheres. The TB(ν) of A stars are consistent with the photospheric model, as seen in Fig. 1 for α CMa. We need more data for young stars to study their physical trends.

thumbnail Fig. 2.

αmm vs. physical parameters with respective power-law fits for the old group (> 1 Gyr). Smaller markers denote stars < 1 Gyr.

In addition, Fig. 3 compares αmm with common activity indicators. The error intervals on log RX and 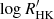were estimated based on the results on their systematic variability for cool stars by Micela & Marino (2003) and Pace (2013), respectively. The relatively low errors on αmm help distinguish the cool stars much better than other indicators and they provide robust quantitative maps to physical parameters.

thumbnail Fig. 3.

Comparison of αmm value ranges with those in and log RX for cool star sample. The markers used are the same as in Fig. 2.

4. Discussion

Stars are believed to evolve from a high- to low-activity phase with age, due to continuous loss of energy and angular momentum, which is reflected in the rise of the rotation period with age (e.g., Skumanich 1972; Stepien 1994; Davenport 2016; van Saders et al. 2016). Barnes (2003) classified this age-related activity evolution by analysing the shift in the distribution of stars in a rotation period vs. B − V plane for stars of different age ranges. The two groups of distributions that emerged were named ‘I’, the fast rotating high-activity group, and ‘C’, the slow rotating low-activity group. It was found that stars tend to evolve from ‘C’ to ‘I’ as they age, with hotter stars evolving faster. However, F–K dwarfs older than 1 Gyr were found to have migrated to the ‘I’ branch. In our cool star sub-sample, we find that the old group shows robust physical trends with physical parameters, to which the lone young star, ϵ Eri, does not agree. ϵ Eri also shows a significantly higher αmm. Since TB(ν) of cool stars is a proxy to their chromospheric thermal structure and since the spectral index, αmm, quantifies the thermal gradients, the relatively high αmm of ϵ Eri hints at higher atmospheric heating and activity.

4.1. Physical dependencies of αmm for old cool stars

Cooler stars (lower Teff) are expected to be more active due to their stronger magnetic fields. The αmm estimates are higher for cooler stars, probably hinting at more efficient heating mechanisms which can sustain stronger chromospheric thermal gradients, as well as higher levels of steady heating and activity. Similarly, stars with higher B − V have higher αmm. We find that αmm increases with period, as opposed to the well-known anti-correlation between activity and rotation period. Also, stars with higher surface gravity (g) show higher αmm. Since activity is related to the observed rotation rates (v sin i; i is the inclination angle with respect to the line of sight), g and Teff, analysing the individual parameter trends with αmm may not provide a coherent picture, especially in view of the small sample size.

In Fig. 4a, αmm is compared to (v sin i)2/(Rg), the ratio of surface rotational kinetic energy relative to the gravitational potential. Stars with higher αmm tend to show lower relative rotational kinetic energy. Figure 4b shows αmm vs. the scale height H = kTeff/(μmpg), where k is the Boltzmann constant, μ is the mean molecular weight (here μ = 0.5), and mp is the proton mass. We find that αmm increases with decreasing H.

thumbnail Fig. 4.

αmm vs. (v sini)2/(Rg) and H. Markers are the same as in Fig. 2

Meanwhile, since i values are unknown for the F dwarfs in the sample, the trends in the period and (v sin i)2/(Rg), will be affected by the projection effect (sin i). Also we need multi-frequency data for the F dwarfs in the sample to make a robust αmm estimate. A large multi-frequency sample of A- to M-type stars, with known i, spread across wide ranges in age, Teff, period, and g is needed to draw statistically significant conclusions. The A stars in such a sample will help explore the physics of emergence of hot chromospheres (Simon et al. 2002) traced by αmm becoming positive.

4.2. Towards a robust mm-band activity indicator

A robust activity indicator should not only provide a reliable quantitative scale, but also map the activity levels to physical parameters robustly, in a way that it facilitates clear segregation of stars in the planes of activity vs. different physical parameters. We considered two pairs of stars with quite similar Teff and spectral types, and a good estimation of αmm errors: α Cen B and ϵ Eri (Pair 1: K type, Teff ∼ 5000 K), and α Cen A and the Sun (Pair 2: G type, Teff ∼ 5800 K). The stars in each pair differ among each other in physical parameters other than Teff. Each pair of stars is well separated along the αmm axis, despite estimation errors. In the case of Pair 1, ϵ Eri belonging to the more active ‘C’ branch has relatively high TB values for similar frequencies and higher αmm than α Cen B. Meanwhile, for Pair 2 comprised of old stars, in planes formed by their differentiating physical parameters (g, rotation period, B − V) with αmm (Figs. 2b–d), the stars align well along the best-fit power-law trends. This property of alignment along best-fit trends is even seen for the binary pair γ Vir A and B which have similar physical properties, except for g. γ Vir A with a slightly higher g has a slightly higher αmm than its companion. A physical characterisation of cool stars to this accuracy is difficult with common indicators due to the large value intervals (Fig. 3), and especially for stars within the narrow Teff range of 5000–7000 K explored here.

As mentioned earlier, the error intervals on αmm capture the effect of stellar variability within activity cycle periods for the Sun, ϵ Eri, and the α Cen binary. It is found that the error interval is the highest for the most active young star, ϵ Eri, possibly hinting at a higher variability in its activity level during the stellar activity cycle. This agrees well with the current consensus that young ‘C’ branch stars usually show higher variability in activity indicators than the older ‘I’ branch during their activity cycles (e.g., Pace 2013). So, while the αmm estimates provide a quantitative physical characterisation of the mean stellar activity, the error intervals reflect the variability across activity cycles. We need more multi-epoch data for stars in different activity branches to explore mm-TB(ν) and αmm variability.

5. Conclusions and outlook

It is difficult to derive robust quantitative correlations between stellar activity and physical parameters using the common activity indicators. This study explores the possibility of defining a robust activity indicator based on continuum radiation at mm wavelengths using its unique tomographic potential to trace the thermal emission from the various stellar chromospheric layers as a function of observing frequency.

The mm stellar sample compiled by Mohan et al. (2021) was used for the study. The compiled TB(ν) data come from observations done over years, providing chromospheric thermal profiles averaged over activity cycle timescales. The cool stars showed a spectral steepening towards lower frequencies, as expected from an atmosphere that gets progressively hotter towards higher heights (explored by lower frequencies). We derived the mm-TB(ν) spectral index, αmm, for the cool stars, which is expected to characterise the chromospheric thermal gradients and in turn the efficiency of atmospheric heating and activity. Robust power-law functions could be derived for αmm with different activity influencing physical parameters, namely Teff, g, and the rotation period. In addition, αmm shows an inverse correlation with the scale height and the ratio of surface rotational kinetic to potential energy; however, this finding should be interpreted with caution in view of the small sample size. Due to insufficient data, this analysis could only be done for the cool stars older than 1 Gyr. However, the young cool star, ϵ Eri, is well apart from the trends of the old group.

The estimation errors on αmm are quite small in comparison to those in common activity indicators, which facilitated the robust activity quantification and mapping to physical parameters. Even the stars with similar values for some physical parameters, such as the rotation period and Teff, among others, could be well separated in the αmm axes. Also, with more data for A-type stars, the emergence of chromospheres can be explored by tracking the change of sign in αmm as a function of physical parameters.

To conclude, αmm could be developed into a robust activity indicator giving us vital insights into the links between stellar activity, atmospheric structure, and physical properties, especially for cool stars. To assert this, we need more observations and preferably a campaign to monitor nearby cool stars in the mm band at multiple epochs sufficient to sample their variability within respective activity cycles.

Acknowledgments

This work is supported by the Research Council of Norway through the EMISSA project (project number 286853) and the Centres of Excellence scheme, project number 262622 (“Rosseland Centre for Solar Physics”). We acknowledge helpful discussions among the ISSI international team 387 “A New View of the Solar-stellar Connection with ALMA”, which was funded by the International Space Science Institute (ISSI, Bern, Switzerland). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.00170.S, #2016.1.00441.S, #2013.1.00645.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC(Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in co-operation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We thank the referee, Jeffrey L. Linsky, for his valuable comments and suggestions.

References

  1. Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]
  2. Bashi, D., Zucker, S., Adibekyan, V., et al. 2020, A&A, 643, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Davenport, J. R. A. 2016, ApJ, 829, 23 [Google Scholar]
  4. De Pascale, M., Worley, C. C., de Laverny, P., et al. 2014, A&A, 570, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Donati, J. F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [Google Scholar]
  6. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Grießmeier, J. M., Stadelmann, A., Motschmann, U., et al. 2005, Astrobiology, 5, 587 [CrossRef] [Google Scholar]
  8. Hauschildt, P. H., & Baron, E. 1999, J. Comput. Appl. Math., 109, 41 [NASA ADS] [CrossRef] [Google Scholar]
  9. Lammer, H., Lichtenegger, H. I. M., Kulikov, Y. N., et al. 2007, Astrobiology, 7, 185 [NASA ADS] [CrossRef] [Google Scholar]
  10. Linsky, J. L. 2017, ARA&A, 55, 159 [Google Scholar]
  11. Loukitcheva, M., Solanki, S. K., Carlsson, M., & Stein, R. F. 2004, A&A, 419, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Marsden, S. C., Petit, P., Jeffers, S. V., et al. 2014, MNRAS, 444, 3517 [Google Scholar]
  13. Micela, G., & Marino, A. 2003, A&A, 404, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Mohan, A., Wedemeyer, S., Pandit, S., Saberi, M., & Hauschildt, P. H. 2021, A&A, 655, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Moschou, S.-P., Drake, J. J., Cohen, O., et al. 2019, ApJ, 877, 105 [NASA ADS] [CrossRef] [Google Scholar]
  16. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [Google Scholar]
  17. Odert, P., Leitzinger, M., Guenther, E. W., & Heinzel, P. 2020, MNRAS, 494, 3766 [NASA ADS] [CrossRef] [Google Scholar]
  18. Pace, G. 2013, A&A, 551, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [Google Scholar]
  20. Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2002, ApJ, 579, 800 [NASA ADS] [CrossRef] [Google Scholar]
  21. Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
  22. Stepien, K. 1994, A&A, 292, 191 [NASA ADS] [Google Scholar]
  23. Suresh, A., Chatterjee, S., Cordes, J. M., Bastian, T. S., & Hallinan, G. 2020, ApJ, 904, 138 [Google Scholar]
  24. Tapia-Vázquez, F., & De la Luz, V. 2020, ApJS, 246, 5 [CrossRef] [Google Scholar]
  25. Trigilio, C., Umana, G., Cavallaro, F., et al. 2018, MNRAS, 481, 217 [NASA ADS] [CrossRef] [Google Scholar]
  26. van Saders, J. L., Ceillier, T., Metcalfe, T. S., et al. 2016, Nature, 529, 181 [Google Scholar]
  27. Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [Google Scholar]
  28. Vidotto, A. A., Jardine, M., Morin, J., et al. 2013, A&A, 557, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Vidotto, A. A., Gregory, S. G., Jardine, M., et al. 2014, MNRAS, 441, 2361 [Google Scholar]
  30. Wedemeyer, S., Bastian, T., Brajša, R., et al. 2016, Space Sci. Rev., 200, 1 [Google Scholar]
  31. White, S. M. 2004, New Astron. Rev., 48, 1319 [CrossRef] [Google Scholar]
  32. White, S. M., Iwai, K., Phillips, N. M., et al. 2017, Sol. Phys., 292, 88 [Google Scholar]
  33. White, J. A., Tapia-Vázquez, F., Hughes, A. G., et al. 2020, ApJ, 894, 76 [NASA ADS] [CrossRef] [Google Scholar]
  34. Zendejas, J., Segura, A., & Raga, A. C. 2010, Icarus, 210, 539 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

mm-TB(ν) in the 30–1000 GHz range. Titles show the names and spectral types. Family of power-law functions consistent with the αmm estimation errors (shaded regions) and photospheric models (dotted line) are shown. For the Sun, chromospheric FAL models are shown. Multi-epoch data at ν are coloured differently.
In the text
thumbnail Fig. 2.

αmm vs. physical parameters with respective power-law fits for the old group (> 1 Gyr). Smaller markers denote stars < 1 Gyr.
In the text
thumbnail Fig. 3.

Comparison of αmm value ranges with those in and log RX for cool star sample. The markers used are the same as in Fig. 2.
In the text
thumbnail Fig. 4.

αmm vs. (v sini)2/(Rg) and H. Markers are the same as in Fig. 2
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.