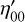| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A143 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202243972 | |
| Published online | 23 August 2022 | |
Differential astrometry with Gaia
Investigating relativistic light deflection close to Jupiter
1
INAF - Osservatorio Astrofisico di Torino,
Via Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: ummi.abbas@inaf.it
2
ALTEC S.p.a,
Corso Marche, 79,
10146
Torino, Italy
Received:
6
May
2022
Accepted:
14
June
2022
Aims. In this paper, we develop a differential astrometric framework that is appropriate for a scanning space satellite such as Gaia. We apply it to the first of the GAREQ fields – the Gaia Relativistic Experiment on Jupiter’s quadrupole – which is the fruit of dedicated efforts within the Gala project focused on measuring the relativistic deflection of light close to Jupiter’s limb. This provides a preliminary assessment of the following: a) the observability of the relativistic deflection of light close to Jupiter and b) Gaia’s astrometric capabilities under extremely difficult conditions such as those around a bright extended object.
Methods. Inputs to our differential astrometric model are the charge-coupled device (CCD) transit times as measured by the intermediate data update (IDU) system, transformed to field angles via astrometric global iterative solution (AGIS) geometric calibrations, and the commanded or nominal spacecraft attitude. Actual attitude rates, including medium and high-frequency effects, were estimated from successive CCD pair observations and used to transfer the field angles onto intermediate tangent planes, finally anchored to a common reference frame by fitting a six-parameter model to a set of suitable reference stars. The best-fit parameters provide the target star’s deflection as a time-varying systematic effect. To illustrate the model, we analyzed Gaia astrometric measurements after their calibration through the latest cyclic early data release EDR3/DR3 processing of the GAREQ event in February 2017. We used observations of the closest bright target star successfully observed several times by Gaia in close proximity to Jupiter and surrounding reference stars brighter than G < 13 mag in transits leading up to the time of closest approach and on subsequent transits.
Results. The relativistic deflection signal is detected with a signal-to-noise ratio (S/N) of 50 at closest approach by the target star. This signal is the combined effect due to Jupiter and the Sun, mainly dominated by Jupiter’s monopole, demonstrating Gala’s scientific performance under extreme observational conditions. It is an unprecedented detection for the following reasons: a) it is the closest ever to Jupiter’s limb (~7″) in the optical and b) the highest S/N at any wavelength. Finally, this work sets the stage for investigations into disentangling the relativistic quadrupole deflection due to Jupiter with future Gaia astrometric measurements.
Key words: astrometry / methods: data analysis / reference systems
© U. Abbas et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The Gaia space satellite is currently taking measurements of 1.8 billion sources brighter than G < 21 mag (Gaia Collaboration 2021) and is set to provide their five-parameter global astrometric solutions to unprecedented precision, continuously improving with each data release (DR). The global measurement principle of Gaia for such a large number of stars has led to the need for a sophisticated machinery that entails the astrometric global iterative solution (AGIS) and involving a block-iterative least-squares solution of the astrometric, attitude, calibration, and global parameters in a cyclic manner until convergence (Lindegren et al. 2012). If one is only interested in a small field of sources, then differential astrometry can be used to model transient astrometric events and/or unmodeled systematic effects.
In the context of differential astrometry, a small field inertial reference frame prior to studying such physical effects must be established, for example in cluster membership studies, detecting the reflex motion of the host star due to its planets, obtaining trigonometric parallaxes, measuring the relativistic deflection of light due to giant planets to name a few (see Abbas et al. 2017 and references therein). For space-based observations and in the absence of Earth s atmosphere, many problems are avoided; nonetheless, there are effects due to the following: a) light aberration on the order of ~20 arcseconds to first order and few mas to second order (Lattanzi et al. 1993); b) gravitational deflections due to various moments of giant planets and the Sun (Crosta & Mignard 2006); c) parallaxes and proper motions of stars (Lattanzi et al. 1993; van Altena et al. 2013); and d) changes in the geometric instrument model due to imperfections in the optics, charge-coupled device (CCD) structure, or positioning, as well as thermal variations in the instrument (Lindegren et al. 2012).
According to Crosta & Mignard (2006), the motion of a giant planet such as Jupiter along its orbit causes favorable scenarios where Jupiter, as seen by Gaia, lies in close proximity (i.e., within 10arcsec from its limb) to relatively bright stars. Under such conditions, the Gaia Relativistic Experiment on Quadrupole (GAREQ) light deflection (at that epoch known as GAREX - Gaia Relativistic Experiment) was designed in order to study the deflection of “grazing” starlight due to Jupiter’s monopole and quadrupole moment. Firstly, a galactic model was used and, secondly, a restricted field of stars was chosen from a real catalog (GSC2; Lasker et al. 2008) in order to simulate the detection of the effect due to a bright star passing close to Jupiter’s limb (Crosta et al. 2008). Such situations generally arise as Gaia scans the sky close to the galactic plane and depend on the initial scanning law parameters (de Bruijne et al. 2010). The follow-up optimization campaign carried out by the dedicated RElativistic Modeling And Testing (REMAT) working group within the Data Processing Analysis Consortium (DPAC) of Gaia with a further fine-tuning of the spin phase led to the predicted favorable configuration of three stars with G < 15.75 mag close to Jupiter’s limb for February 2017 (Klioner & Mignard 2014a,b; Abbas et al. 2014). The high-cadence observations obtained by Gaia in February 2017 were highly successful with some barely a few arcseconds from Jupiter’s limb, despite the stray light from the extremely bright Jupiter disk that strongly affects observations within a couple of arcseconds from its limb even capable of washing out any given observation entirely.
The first detection of relativistic deflection by a body other than the Sun, that is to say Jupiter, was seen in the near-occultation event on 21 March 1988 with the Very Long Baseline Interferometry (VLBI) measurements, when the ray path of the radio source P0201 + 113 came within 200 arcsec of Jupiter (Treuhaft & Lowe 1991). In that case, the expected gravitational bend of the ray path according to general relativity, averaged over the experiment duration, was approximately 300 μarcsec with measurement accuracies on the order of 160 μarcsec. Other attempts in the optical with the Hubble Space Telescope were made (Whipple et al. 1996), but the results of which were never published.
In the spirit of Abbas et al. (2017) where the authors made a first attempt at using simulated Gaia measurements to look at the short-term stability of a differential astrometric reference frame, we decided to adopt a similar approach and study the stability of the small field reference frame and the relativistic deflection of light during the GAREQ event from February 2017. In our differential analysis, we focus on the closest, brightest star with G = 12.78 mag (hereafter referred to as the target star) that was seen a total of 26 times over a 2-month period starting at the beginning of 2017, out of which we used 25 transits over a short time interval of roughly 3 days surrounding the observation at closest approach.
The paper is divided as follows: Sect. 2 presents the alldifferential astrometric framework. Section 3 shows the details of the Gaia observations that are subsequently used in the model and their cleaning. Section 4 describes the physical and instrumental effects on the observations. Section 5 illustrates the relativistic deflection of light during the GAREQ event. Section 6 discusses the error budget due to the reference stars and, finally, the conclusions are provided in Sect. 7.
2 The all-differential astrometric model
The fundamental ingredients to the differential astrometric model are the Satellite Reference System (SRS) field angles, 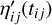 and
and 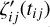 , of the jth star in the ith frame1, in the along (AL) and across (AC) scanning directions, respectively, with the best available geometric calibration at each on-board mission timeline (OBMT)2 observation time tij (a description of how these are obtained is given in the next section). The target star as measured in the ith frame is denoted by
, of the jth star in the ith frame1, in the along (AL) and across (AC) scanning directions, respectively, with the best available geometric calibration at each on-board mission timeline (OBMT)2 observation time tij (a description of how these are obtained is given in the next section). The target star as measured in the ith frame is denoted by 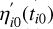 and
and 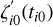 .
.
All the field angles at different times within a given frame need to be referred to the observing time unique to that frame (for convenience, we chose this to be the observing time ti0 of the target star for that frame). This is done by applying a correction to the field angles which depends on their rate of change, that is,
![$\matrix{ {{{\eta '}_{ij}}\left( {{t_{i0}}} \right) = {{\eta '}_{ij}}\left( {{t_{ij}}} \right) + \sum\limits_{{t_{i0}}}^{{t_{ij}}} {\dot \eta \,\left[ {\eta \left( t \right),\zeta \left( t \right),t} \right]} \,{\rm{\Delta }}t} \cr {{{\zeta '}_{ij}}\left( {{t_{i0}}} \right) = {{\zeta '}_{ij}}\left( {{t_{ij}}} \right) + \sum\limits_{{t_{i0}}}^{{t_{ij}}} {\dot \zeta \,\left[ {\eta \left( t \right),\zeta \left( t \right),t} \right]} \,{\rm{\Delta }}t,} \cr } $](/articles/aa/full_html/2022/08/aa43972-22/aa43972-22-eq5.png) (1)
(1)
with Δt chosen to be 1 s.
The field-angle rates are expressed by the following analytical formulae (see Lindegren et al. 2018, Eq. (4)):
![$\matrix{ {\dot \eta \left[ {\eta \left( t \right),\zeta \left( t \right),t} \right] = - {\omega _z}\,{\rm{ + }}\,\left[ {{\omega _x}\cos \varphi \,{\rm{ + }}\,{\omega _y}\,{\rm{sin}}\varphi } \right]\,\tan \zeta \left( t \right)} \hfill \cr {\dot \zeta \left[ {\eta \left( t \right),\zeta \left( t \right),t} \right] = - {\omega _x}\sin \varphi \,{\rm{ + }}\,{\omega _y}\cos \varphi ,} \hfill \cr } $](/articles/aa/full_html/2022/08/aa43972-22/aa43972-22-eq6.png) (2)
(2)
where ωx, ωy, and ωz are the components of the instantaneous inertial angular velocity of Gaia and φ = η ± γ/2, where the plus or minus sign is used for the preceding (P) and following (F) field of view (FOV), respectively, and with γ being the basic angle3.
Estimates of the inertial angular rate along the SRS axes x, y, and z are obtained from pairs of successive CCD observations in the astrometric field (AF) of the same source with corresponding successive observation times (further detailed in Sect. 3.2 of Lindegren et al. 2018). In short, this involves a two-step procedure whereby the measured rates are first reduced to the center of the field (where η = ζ = 0), and then transformed to the inertial angular velocity components in a second step. At the field center, 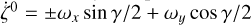 , which when subtracted from ζ gives
, which when subtracted from ζ gives
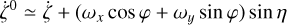 (3)
(3)
after neglecting second order terms in η2. Furthermore, ζ are essentially the raw rates that are calculated using all suitable AC pair observations, and they are simply the differences in the AC field angle between pairs of successive CCD observations divided by their corresponding time differences. Using Eq. (3), these are then corrected for the field rotation by means of the commanded inertial angular rates ωx and ωy. For each FOV, the values 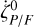 are sorted by time and the running n-point medians are computed to obtain arrays of
are sorted by time and the running n-point medians are computed to obtain arrays of 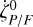 from which the required value can be interpolated.
from which the required value can be interpolated.
Subsequently, ωx, ωy can then be calculated as follows:
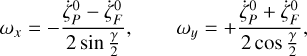 (4)
(4)
where the required value of 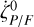 is interpolated to the time of the rate estimate.
is interpolated to the time of the rate estimate.
The same procedure is adopted for ωz, using
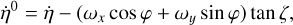 (5)
(5)
where 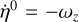 has been replaced in Eq. (2) and is calculated using the AL raw rates
has been replaced in Eq. (2) and is calculated using the AL raw rates 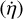 and the improved rates ωx, ωy from Eq. (4) above. The rate measurements,
and the improved rates ωx, ωy from Eq. (4) above. The rate measurements, 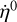 , are binned by time, using a bin size of 0.5 s, and the median values are calculated in each bin providing an accurate time series representation of ωz(t). This bin size is for the maximum time resolution and just large enough to allow for a reliable (robust) estimate per bin, requiring a minimum of ten to 20 values per bin.
, are binned by time, using a bin size of 0.5 s, and the median values are calculated in each bin providing an accurate time series representation of ωz(t). This bin size is for the maximum time resolution and just large enough to allow for a reliable (robust) estimate per bin, requiring a minimum of ten to 20 values per bin.
An example of the effectiveness of this procedure is shown as the orange line in Fig. 1 for the first transit of the target star during the GAREQ event in February 2017 (for more examples, see Appendix A of Abbas et al. 2021). This can be compared to the third on-ground attitude determination (OGA3.2) AL rate and the good agreement demonstrates the accuracy in obtaining the AL rates in this manner.
Once the field angles of each star have been transformed to their proper frame time, we estimate and remove a priori the effects due to Gaia EDR3 proper motions (PMs) and parallaxes (Sect. 2.1). These field angles are then transformed by a rotation and then a gnomonic transformation (Sect. 2.2). The least-squares fitting procedure then involves the Taylor series expansion of the transformed field coordinates (Sect. 2.3) and finally a linear plate transformation onto the reference frame (Sect. 2.4).
 |
Fig. 1 CCD pair scan AL rates for transit number 1. The green and magenta points show the pair scan rates for FOV1 and FOV2, respectively, while the rate medians obtained in bins of 0.5 s for these measurements is shown by the orange line that connects each point separated by 1 s. The black dashed line shows the AL rate, as obtained with OGA3.2 (including the corrective attitude), at the same times as for the orange line. |
2.1 A priori removal of parallaxes and proper motions
Here, we show the procedure of removing, a priori, the parallaxes and PMs from Gaia EDR3. This step is necessary as unmodeled astrometric parameters add systematic effects with unmodeled PMs which have a stronger effect than unmodeled parallaxes, ~23 μas (AL) and 69 μas (AC), due to unmodeled PMs versus the ~5 μas (AL) and 17 μas (AC) due to unmodeled parallaxes (Abbas et al. 2019). These quantities are given in equatorial coordinates which then need to be converted to the SRS giving the projected along and across scan values. This transformation for PMs is completely determined by the position angle of the scan (computed from the nominal attitude) and is given by the following:
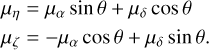 (6)
(6)
When treating the parallaxes, μα and μδ can be replaced with the parallax factors fα and fδ, respectively, calculated using star catalog values and Gaia ephemerides, to obtain the transformed parallax factors along and across the scanning direction. The “corrected” field angles are then given as follows:
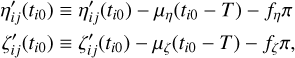 (7)
(7)
where 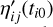 and
and 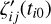 at time ti0 on the RHS are calculated as given at the very beginning of this section, and T = t10 is the observing time of the target star on the first frame (arbitrarily chosen).
at time ti0 on the RHS are calculated as given at the very beginning of this section, and T = t10 is the observing time of the target star on the first frame (arbitrarily chosen).
2.2 Prerotation and gnomonic transformation
Before trying a global adjustment of all the frames using the principles of tangent-plane astrometry, field angle measurements must be rectified via a gnomonic transformation. In order to minimize the differential effect of the so-called tilt terms, which are second-order quantities arising from a misalignment of the nominal versus true position of the telescope s optical axis, all the reference stars, including the target, are rotated in such a way that the position of the target star becomes aligned with the (1, 0, 0) vector defining the origin of the η, ζ coordinates.
Then these field angles are converted to standard coordinates in the tangent plane with tangent point (0, 0) using the gnomonic transformations
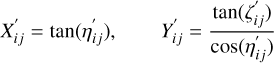 (8)
(8)
for the ith frame and the jth star at the time ti0 of the target star for that frame (the time index is not taken into account from now on as all the times hereafter refer to this time).
List of Observed transits for the target star close to Jupiter.
2.3 Taylor series expansion
We linearize the expressions from Eq. (8) and perform a Taylor series expansion of the reference star coordinates in the tangent plane from above around the calibrated position of the star. The expansion to first order can be written as follows:
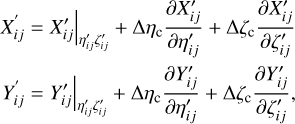 (9)
(9)
where the terms Δηc and Δζc; are treated as unknowns that are simply small corrections to the calibrated field angles, whereas the partial derivatives are evaluated at the calibrated position. Upon closer investigation, we found that the estimated values of the calibration unknowns are rather insignificant (at the sub-µas level) and hence these were eliminated, thereby leaving us with only the first term.
2.4 The differential astrometric model
The positions of the stars in each frame, at time ti0, are therefore adjusted to its reference frame value through a simple plate transformation given as
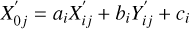
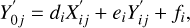 (10)
(10)
where 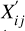 . and
. and 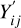 . are the star coordinates in the tangent plane, with
. are the star coordinates in the tangent plane, with 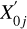 . and
. and 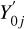 . being the coordinates of the jth star on the reference frame, and the linear plate constants are given by ai, bi, ci, di, ei, and fi. The “transformed” field coordinates,
. being the coordinates of the jth star on the reference frame, and the linear plate constants are given by ai, bi, ci, di, ei, and fi. The “transformed” field coordinates, 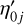 and
and 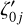 , at times ti0, are then obtained through the inverse gnomonic transformation (from Eq. (8)).
, at times ti0, are then obtained through the inverse gnomonic transformation (from Eq. (8)).
The traditional all-differential approach that has been published in Abbas et al. (2019) typically defines a “plate” as all stars clocked by a single fiducial CCD line, that is to say each FOV transit consists of nine plates from AF1-9. This is the reason why a linear plate adjustment accounts for rotations and translations between the various plates. If one uses the AL-AC rate to account for the rotation over one transit, that is for AF1-9, then the transit itself can be treated as a plate.
There are 90 unknown linear plate parameters (by treating each transit as a plate) that need to be estimated and a total of 3364 AF1-9 observations (after removing flagged observations) from the 15 transits in Table 1 (further described in the following section). The software package GAUSSFit (Jefferys et al. 1988) is used to solve this set of equations through a generalized least-squares procedure weighted according to the input errors (obtained from the standard errors in the calculation of the AL-AC centroid in AF1-9, as estimated by the centroiding algorithm of the Gaia processing pipeline). GAUSSfit uses an iterative process whose convergence is controlled by the input tolerance. Moreover, we performed an external iteration loop to reject outliers until a low-skewness (<0.1) Gaussian distribution of the residuals was achieved. On average, anywhere from 0.04% to 1.5% (depending on the field of interest) of the observations are deemed problematic and not used in the final fit. The estimated plate or frame parameters (ai through fi) allow one to transport the calibrated observations (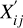 ,
, 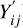 ) to a common reference frame. If all other effects are properly modeled, the distribution of residuals should show the unmodeled Sun and Jupiter monopole (plus Jupiter quadrupole) deflection terms of the reference stars that have not been subtracted out. As can
) to a common reference frame. If all other effects are properly modeled, the distribution of residuals should show the unmodeled Sun and Jupiter monopole (plus Jupiter quadrupole) deflection terms of the reference stars that have not been subtracted out. As can
be expected, it is found that ai and ei are almost unity, whereas bi = −di and together they give the rotation and orientation. The offsets ci and fi· give the offset of the common system. One can try to further reduce the number of unknown plate or frame parameters by imposing a pure rotation and scale; we found that this gives similar results.
 |
Fig. 2 Scene around the target star successfully detected onboard during the transit on 2017-02-22T19:08:12.954 (UTC) at a predicted angular distance of 67.65j from Jupiter’s limb. We note the gap between the detectors in CCD rows 6 and 7. Whilst Jupiter was observed in row 6, the target star happened to be scanned in row 7. Image credit: ESA/Gaia/DPAC/C. Crowley. |
3 Handling the observations
To illustrate the differential model developed, we use the astro-metric measurements taken by the AF CCD detectors in the Gaia focal plane (see Fig. 3 in Lindegren et al. 2021). These observations are taken in time-delayed integration (TDI) mode, so as to allow for the accumulation of charge as the images move across the CCDs due to the spinning motion of Gaia (Gaia Collaboration 2016a). The fundamental astrometric observational quantity is given by the OBMT time corresponding to the passage of a stellar image centroid through the fiducial line of a CCD (typically halfway between the first and last TDI line used in the integration for the CCD), encapsulated in the elementary astrometric observations processed by the intermediate data update (IDU) system. For each transit, nine observations were obtained from Cols. (1)–(9) from AF. The input AF observations are given in the window reference system (WRS) that contains information on each detection, more specifically the CCD, pixel, gate, and FOV of Gaia (see Fabricius et al. 2016 for full details). This information is used, along with the instrumental calibrations from the cyclic processing by AGIS, to convert the star’s observing time into its position in the SRS system, in other words the calibrated field angles in the AL and AC scanning directions (Lindegren et al. 2021) that are ultimately useful for this analysis.
The η(AL) and ζ(AC) field angles mentioned above are essentially the spherical coordinates on the sky relative to a reference direction in each FOV (Lindegren et al. 2012). They represent the fundamental input to the model along with an ulterior adjustment using the commanded or nominal attitude (the reason for this operation is further described in Sect. 2).
We remind the reader that Gaia s astrometric instrument is optimized for measurements in the AL scanning direction, with rectangular pixels that are three times larger in the AC direction (Gaia Collaboration 2016b). This translates into larger uncertainties in the AC observations versus those in the AL direction. Furthermore, only stars brighter than G < 13 mag have two-dimensional windows resulting in accurate AC positional information (accurate AL measurements are always available). Fainter stars are typically acquired as one-dimensional in the AF due to the onboard removal of AC position information by on-chip binning. At the faint end, some “calibration” stars sporadically have two-dimensional information, otherwise one-dimensional windows always come with the Sky Mapper AC observations, providing an approximate position in the AC direction at the pixel level.
We selected stars surrounding the target star during the GAREQ event from February 2017 based on their observation times of lying within a chosen interval for any given time of observation of the target star shown in Table 1. This table also gives the estimated distance from Jupiter s center for the 15 transits that were used in this study. There are two transits that were predicted and not observed by Gaia due to different reasons; in one case, the observation was contaminated by a Jovian Moon lying almost on top of the star and, in the other case, it fell in the gap between CCD rows (Crowley et al. 2017). Figure 2 is an example of the scene around the target star successfully
detected onboard during the first transit in Table 1 and shows the various effects of heavy saturation in the detection record overlay.
Figure 3 shows the stars with magnitudes 10 < G < 13 surrounding the target star based on such a selection, in this case 40 s. Superposed on the same field are the estimated Jupiter positions (Gaia-centric) from the INPOP10 ephemeris file at the observed OBMTs of the target star as seen in January and February 2017, including the 15 transits from Table 1. The single large red point in the left half of the figure corresponds to a single transit by Jupiter in January; the line of 25 consecutive large red points (several pairs of which are overlapping) on the right side instead correspond to the February transits. The last 10 transits are used in the error-budget analysis, as they allow one to study the different systematics produced by Jupiter still in the field, but further away (>300arcsec); this is further discussed in Sect. 6. All AF observations were used after properly cleaning them as mentioned in the next paragraph. The differential analysis was carried out using the stars shown in Fig. 3, that is to say bright stars that have 2D windows and therefore the AL (η) and AC (ζ) coordinates.
The observations have various flags based on the onboard acquisition and processing results at the transit and CCD level. In general, we found that it was necessary to clean the observations that had cosmetic issues in the processing and with saturated samples removed. At times there were also some observations due to an abnormal charge injection preceding the window in the acquisition. Furthermore, only observations with goodness-of-fit values of the image fit to the point and line spread function (PSF and LSF) model of less than 100 were retained in order to eliminate the few extreme outliers. The target star of interest had a few similar flags, as well as some due to a non-nominal gate4 in the window and multiple gates, especially when it was observed closest to the limb of Jupiter, that is to say TransitId 3 of Table 1.
 |
Fig. 3 Star field surrounding the brightest star closest to Jupiter’s limb in the magnitude range of 10 < G < 13 mag within o.8 × 1.3 deg on the sky along with Jupiter using the INPOP10 ephemeris. The small green star symbols show the stars, the big red dots denote Jupiter’s position as seen on each transit by Gaia when the target star was observed (the single large red dot on the left is the January transit, and the set of 25 dots in the center are the February transits), and the target star is shown as the large blue star at α = 201.41, δ = −7.38 deg. |
4 Physical and instrumental effects
The measurements are generally affected by astrometric effects, such as velocity aberration and gravitational light deflection, and by the proper motions and parallaxes of the sources which can all be classified as physical effects. They are also subject to instrumental errors that require accurate modeling. We briefly summarize both of these effects, but for more details please refer to Sect. 3 of Abbas et al. (2017).
4.1 Physical effects
Aberration is by far the dominant effect and is caused by the motion of the observer with respect to the barycenter of the Solar System (Klioner & Kopeikin 1992; see also Appendix in Lattanzi et al. 1993). It is roughly on the order of v/c to first order. For the speed of Gaia (≃29.6 km s−1), the maximum values (projected values along the AL direction) are roughly 20″. 3 to first order and −2.7 mas to second order, and third order terms are at the 1 μas level.
The gravitational deflection of light due to Solar System objects is another major effect that needs to be taken into account and depends on the angular separation between the Solar System body and the given source. In the GAREQ field, mainly Jupiter and the Sun give contributions, where the dominant deflection effect is Jupiter reaching 16.2 mas at its limb and falling off as the inverse of the impact parameter (principally due to Jupiter s monopole; the quadrupole deflection effect is barely 240 μas at the limb which instead decreases as the inverse cube of the impact parameter). The deflection due to the Sun amounts to ~1.8 mas (with a 0.3−0.6 mas effect in AL) as seen by Gaia for this GAREQ field. Over timescales of 24 h, differential aberration is a largely linear effect that amounts to a several mas AL scan for this field (see Fig. 4 in Abbas et al. 2017), whereas the differential gravitational deflection is nonlinear contributing several mas (mainly due to Jupiter’s monopole) with sub-μas being due to Sun s monopole.
The stars PMs can vary up to several hundreds of mas yr−1. For this particular field, the set of reference stars has Gaia EDR3 PMs varying up to 116 mas yr−1 and with parallaxes up to 9 mas. The effect due to PMs is mostly linear and can be on the order of tens of μas over 24 h.
4.2 Instrumental effects
The observation lines, given by the fiducial lines mapped onto the tangent plane, are affected by the geometric instrument model describing the layout of the CCDs. This includes the physical geometry of each individual CCD and its configuration in the focal plane assembly; the distortions and aberrations in the optical system; and the nominal values of the focal length and basic angle, γ (see Lindegren et al. 2012, 2016 for extensive details). These effects are time-dependent and one of three types: large-scale AL calibrations occurring on short timescales; small-scale AL calibrations, which are expected to be stable possibly over the whole mission duration; and large-scale AC calibrations, which are assumed to be constant on long timescales.
As we are considering observations over a few days, we are only concerned with the large-scale AL and AC calibrations that can be considered to be constant to first approximation. The AL (and AC) large-scale calibration is modeled as a low order polynomial in the across-scan pixel coordinate, which varies from 13.5 to 1979.5 across the CCD columns (Lindegren et al. 2012)
The effect due to calibrations is highly nonlinear at the mas level. The handling of the calibrations and unmodeled errors during the cyclic processing by AGIS improves with each cycle (see Fig. 9 in Lindegren et al. 2018 versus Fig. A.1 in Lindegren et al. 2021), and it is significantly better than the calibrations from the daily processing pipelines.
5 The February 2017 GAREQ deflection event
The set of 31 reference stars shown in Fig. 3 are not always seen by Gaia whenever the target star is seen. This is due to a variety of reasons: the way Gaia scans the sky, stars at the edge of the FOV, observations that fall in the gap between two CCD columns, among others. Furthermore, stars seen on any given single transit do not necessarily have all the sequence of nine AF observations for the chosen time interval around the target star. This results in an inhomogeneous set of observations per frame, with some having barely a dozen reference stars in total. We chose ±40 s as the time interval (obtained with the same CCD column) for reference stars surrounding the target star as a good
compromise between maximizing the number of reference stars and minimizing the higher order effects that come into play from larger fields.
Figure 4 depicts the transformed5 AL field angle, 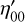 , for the target star at the various observing times for the 15 transits in Table 1, using the best-fit linear plate parameters obtained with the surrounding reference stars. For comparison, we show the overlapping prediction (red curve) obtained with the Gaia relativity model (GREM; Klioner 2003, 2004), which refers to the classical relativistic light deflection effect due to Jupiter and the Sun, with a dominant contribution from Jupiter s monopole. Also shown is the total light deflection (gray curve) due to Jupiter demonstrating the 16.2 mas deflection that would be seen by a grazing light ray at the limb of Jupiter. There is good agreement between the observed and predicted AL deflections for all the transits within the AF1-9 spreaded observations per transit. We find that the signal at closest approach is a factor of 50 times that of the 0.2 mas standard deviation of the observed values over AF2-9 at highest deflection (AF1 has been removed as it is a clear outlier). This is an unprecedented measurement at optical wavelengths in the literature of the relativistic deflection of light due to Jupiter, and the first time at any wavelength for a star ~7″ from its limb.
, for the target star at the various observing times for the 15 transits in Table 1, using the best-fit linear plate parameters obtained with the surrounding reference stars. For comparison, we show the overlapping prediction (red curve) obtained with the Gaia relativity model (GREM; Klioner 2003, 2004), which refers to the classical relativistic light deflection effect due to Jupiter and the Sun, with a dominant contribution from Jupiter s monopole. Also shown is the total light deflection (gray curve) due to Jupiter demonstrating the 16.2 mas deflection that would be seen by a grazing light ray at the limb of Jupiter. There is good agreement between the observed and predicted AL deflections for all the transits within the AF1-9 spreaded observations per transit. We find that the signal at closest approach is a factor of 50 times that of the 0.2 mas standard deviation of the observed values over AF2-9 at highest deflection (AF1 has been removed as it is a clear outlier). This is an unprecedented measurement at optical wavelengths in the literature of the relativistic deflection of light due to Jupiter, and the first time at any wavelength for a star ~7″ from its limb.
A zoomed-in view on the highest set of deflection observations seen on the third transit is shown in Fig. 5, clearly demonstrating that the AF1 measurement is an outlier at the 3-σ level. Once that point was removed, the standard deviation of the points at highest deflection (0.2 mas) then was only slightly lower than that from the points in the remaining 14 transits (~0.25 mas) and from the points in the last 12 transits (~0.22 mas) that are minimally affected by Jupiter.
 |
Fig. 4 AL coordinate for the target star, |
 |
Fig. 5 Zoom-in on the highest deflection observed at the third transit shown in Fig. 4, with the observations being depicted as blue circles and the predicted AL-light deflection by Jupiter as the red line. The numbers accompanying each blue circle denote the corresponding AF column associated with the observation, e.g., 1 means that the measurement is associated with AF1. It can be seen that the AF1 measurement is an outlier at more than 3-σ. |
 |
Fig. 6 Joint AL-AC post-fit residual distribution of the reference stars in the first 15 transits of the GAREQ field (further described in the main text) surrounding the target star and showing σAL = 180 μas and σAC = 1.822 mas. The red shaded ellipse shows the 1σ joint uncertainty. The histogram distributions are shown in the margins: AL is at the top and AC is on the right. |
6 The reference stars’ residual distribution and error budget analysis
The deflection signal seen in the target star mainly depends on the reference stars and their residual distribution; the smaller the uncertainties, the more tight the estimated plate parameters are which lead to a cleaner deflection signal. The target star was seen on a total of 25 (mostly consecutive) transits from February 22 to February 26, 2017 thanks to the optimized scanning law (the
first 15 of which are detailed in Table 1 and shown in Fig. 4). We looked at the residual distribution of the reference stars surrounding the target star under two different circumstances: in the first 15 transits, which includes the highest deflection signal, shown in Fig. 6, and in the following ten consecutive transits shown in Fig. 7.
In the first 15 transits, we find σAL = 180 μas and σAC = 1.822 mas in the post-fit residual distribution with a Pearson’s correlation between the AL and AC residual distributions of 0.275. In the following ten transits, the values decrease to σAL = 162 μas and σAC = 1.469 mas with a Pearson’s correlation of 0.15 between the two residual distributions. Indeed, the bright disk of Jupiter causes extra systematic effects which show up as a very mild correlation in the AL and AC residual distributions of the surrounding reference stars, besides increasing the standard deviation of such a distribution. This extra systematic effect is expected to be accounted for or at least significantly reduced during regular cyclic developments in future data processing. It can be seen that the scale of the AC axis is roughly five times larger than that of the AL axis. We have deliberately maintained this scale difference in the figures in order to better demonstrate the distribution and correlation of the residuals.
 |
Fig. 7 Joint AL-AC post-fit residual distribution of the reference stars in the last 10 transits of the GAREQ field (further described in the main text) surrounding the target star and showing σAL = 162 μas and σAC = 1.469 mas, which is depicted as the red shaded ellipse in the form of the 1-σ joint uncertainty. The corresponding AL and AC histogram residual distributions are shown in the margins. |
6.1 Residual distributions as a function of magnitude
The post-fit residuals in the AL and the AC scanning directions are shown as a function of the reference star s magnitude in Fig. 8. It can be seen that, in general, the outliers in the AL residual distribution have a darker shade of red or blue, indicating that they are also outliers in their AC residuals. The same is not necessarily true in the case of the AC residuals, that is to say the outliers do not always have high values of Δη.
 |
Fig. 8 Post-fit AL (panel a) and AC (panel b) residuals of the reference stars in the 15 transits versus the magnitude of the star. The color coding is as a function of the AL-AC residual value. |
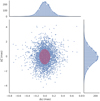 |
Fig. 9 Joint AL-AC post-fit residual distribution of stars in a “quiet” field showing σAL = 150 μas and σAC = 1.213 mas, depicted as the red shaded ellipse in the form of the 1-σ joint uncertainty. The corresponding histogram distributions are shown in the margins. |
6.2 Reference stars in a “quiet” and normal field
We looked at a set of stars in the same magnitude range (10 < G mag < 13), with a similar mean magnitude (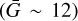 ), in a different and “quiet” field that was also seen on four consecutive transits. This is a field surrounding a star at RA: 92.95 Dec: 22.83 deg and it is quite similar to the GAREQ field as it satisfies the following three main requirements: similar mean magnitude, high-cadence observations, and a large number of (in this field about 200) bright reference stars. A large number is particularly important as not all reference stars are always seen on successive transits. For example, the last two transits have almost 180 reference stars in common, whereas the first two transits have roughly 60 in common. The joint residual distribution (considering goodness-of-fit values of the image fit to the PSF and LSF model of less than 100) is shown in Fig. 9. Indeed, for such a clean field of stars with no extra disturbances, the Pearson’s correlation between the AL and AC residual distribution is 0.03, demonstrating that the presence of Jupiter within ~500 arcsec of the reference stars is enough to introduce extra systematic effects on the order of several tens of μas.
), in a different and “quiet” field that was also seen on four consecutive transits. This is a field surrounding a star at RA: 92.95 Dec: 22.83 deg and it is quite similar to the GAREQ field as it satisfies the following three main requirements: similar mean magnitude, high-cadence observations, and a large number of (in this field about 200) bright reference stars. A large number is particularly important as not all reference stars are always seen on successive transits. For example, the last two transits have almost 180 reference stars in common, whereas the first two transits have roughly 60 in common. The joint residual distribution (considering goodness-of-fit values of the image fit to the PSF and LSF model of less than 100) is shown in Fig. 9. Indeed, for such a clean field of stars with no extra disturbances, the Pearson’s correlation between the AL and AC residual distribution is 0.03, demonstrating that the presence of Jupiter within ~500 arcsec of the reference stars is enough to introduce extra systematic effects on the order of several tens of μas.
We performed a test by using a random subsample of 30 stars for this field, matching the number of reference stars in the GAREQ field. This led to similar residuals (i.e., σAL ~ 142 μas), demonstrating that unmodeled systematics, probably induced by imperfect instrumental calibrations, are the dominant effect which is in line with the robust estimates of the actual standard deviations of the post-fit residuals in EDR3 (see Fig. A.1 in Lindegren et al. 2021).
7 Conclusions
In this paper, we have developed a sophisticated differential astrometric model that is appropriate for a scanning space satellite such as Gaia. In general, the differential setup allows one to study single events in a small field, with a sufficient number of bright reference stars, such as the ones presented here.
This method relies upon a transformation of the astrometric observations of stars (in the form of calibrated field angles) onto tangent planes at various times finally anchored to a common reference frame. Only the commanded or nominal attitude of the spacecraft is used along with generalized least-squares in order to obtain the best-fit plate parameters and the floor of the reference stars. This establishes a small-field reference frame where any additional “systematic effect” can be further studied. We have used this framework to provide a preliminary assessment of the GAREQ event observed in February 2017 by investigating: a) the observability of the relativistic deflection of light close to Jupiter and b) Gaia s astrometric capabilities under critical conditions such as those around an extremely bright extended object.
We use astrometric measurements provided by Gaia of 31 bright reference stars (10 < G mag < 13) over -3 days all lying within a field of 0.8 × 1.3 deg, surrounding a target star (G = 12.78 mag) of particular interest. The bright magnitude limit for the reference stars was imposed mainly by the availability of 2d CCD cutouts (windows in Gaia jargon) providing precise 2D observations and, secondarily, by the overall random astrometric standard errors. We use observations of the bright target star and surrounding reference stars in transits leading up to the time of closest approach to Jupiter s limb and on subsequent transits during the GAREQ event. The best-fit plate parameters obtained using the model ultimately provide the target star’s deflection as a systematic effect.
The target star was successfully observed several times within 5 Jupiter radii from Jupiter s estimated center, 0.35 Jupiter radii (roughly 6.7j) from Jupiter’s limb at closest approach, and it is especially favorable for studying the effects on the relativistic deflection of light from the star as it passes near a giant oblate planet. These special events are being studied within the context of GAREQ with the ultimate goal of disentangling a -100 μas AL signal at closest approach to Jupiter’s limb due to the planet’s quadrupole moment from the much larger ~10 mas monopole deflection.
Here we present the first results of the relativistic light deflection at the ~10 mas level with a reference star residuals’ distribution of σAL ~180 μas. With the present differential astrometric model we find that Jupiter’s monopole deflection dominates the signal obtained using current DPAC processed data from cycle 3 (i.e., EDR3/DR3 astrometry). The event from February 2017 presented here is the first of three predicted events expected to take place over 3 yr of the Gaia nominal mission (the other two were slated for September 2018 and April 2019 and are expected to be covered by future cyclic processed data, cycle 3 processed data were only covered until May 2017). Moreover, by using data from the cyclic reprocessing in future cycles, which will better handle the extra systematic effects arising from Jupiter’s glare in the field, we hope to better study Jupiter’s quadrupole deflection.
Our results show that the scene chosen for the GAREQ event allows for a clean detection of the relativistic deflection of light from a star by Jupiter with a S/N of −50 and in good agreement with the predicted total deflection. This detection is unprecedented as it is: a) the closest ever to Jupiter’s limb (−7″) in the optical and b) with the highest S/N at any wavelength. These results strongly encourage further investigations to search for and disentangle the quadrupole deflection from the total signal using Gaia astrometric observations from future processing cycles.
Acknowledgements
We thank the referee for useful suggestions that helped to improve the paper. We further thank M. Biermann and U. Bastian for valuable suggestions and discussions that helped us refine the differential methodology and the AGIS and IDU teams for the processing and calibration of the data used in this paper. We also thank F. Mignard and S. Klioner for their essential role in the GAREQ experiment and for the optimization of the Gala scanning law that led to the deflection event of February 2017, and C. Crow-ley and his team for demonstrating the exceptional performance of Gaia under the extreme observing circumstances of the scene around Jupiter that led to the successful repeated observations of the target star, including the measurement at 0.35 RJupiter away from the planet’s limb. We acknowledge the support of A. Brown, T. Prusti and G. Gracia throughout the development of this work. UA thanks Alessandro Sozzetti for helpful discussions and brainstorming sessions that helped with an effective implementation of crucial stages of data treatment. This work was financially supported by the European Space Agency (ESA) in the framework of the Gaia project; the Italian Space Agency (ASI) through Gaia mission contracts: the Italian participation to the Gaia Data Processing and Analysis Consortium (DPAC), ASI 2014-025-R.1.2015 and ASI 2018-24-HH.0 in collaboration with the Italian National Institute of Astrophysics. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/Gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Python libraries used: Matplotlib (Hunter 2007), NumPy (Harris et al. 2020), Pandas (Reback et al. 2021) and Seaborn (Waskom 2021).
References
- Abbas, U., Lattanzi, M., & Crosta, M. 2014, QFIND: Optimized scanning law parameters for GAREQ and the influence of non-single stars, Tech. rep., GAIA-C3-TN-INAF-UA-004-01 [Google Scholar]
- Abbas, U., Bucciarelli, B., Lattanzi, M. G., et al. 2017, PASP, 129, 054503 [NASA ADS] [CrossRef] [Google Scholar]
- Abbas, U., Bucciarelli, B., & Lattanzi, M. G. 2019, MNRAS, 485, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Abbas, U., Bucciarelli, B., & Lattanzi, M. 2021, QDIFF-GAREQ: Results on the Protocol Adopted at CU3 Meeting #13, Tech. rep., GAIA-C3-TN-INAF-UA-007-01 [Google Scholar]
- Crosta, M., & Mignard, F. 2006, Classical Quant. Grav., 23, 4853 [CrossRef] [Google Scholar]
- Crosta, M. T., Gardiol, D., Lattanzi, M. G., & Morbidelli, R. 2008, in The Eleventh Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, eds. H. Kleinert, R. T. Jantzen, & R. Ruffini, 2597 [CrossRef] [Google Scholar]
- Crowley, C., Martin-Fleitas, J., & Mora, A. 2017, Onboard detections during the GAREQ event of February 2017, Tech. rep., GAIA-CH-TN-ESA-CMC-019-I [Google Scholar]
- de Bruijne, J., Siddiqui, H., Lammers, U., et al. 2010, in IAU Symposium, 261, Relativity in Fundamental Astronomy: Dynamics, Reference Frames, and Data Analysis, eds. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 331 [Google Scholar]
- Fabricius, C., Bastian, U., Portell, J., et al. 2016, A&A, 595, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jefferys, W. H., Fitzpatrick, M. J., & McArthur, B. E. 1988, Celest. Mech., 41, 39 [Google Scholar]
- Klioner, S. A. 2003, AJ, 125, 1580 [Google Scholar]
- Klioner, S. A. 2004, Phys. Rev. D, 69, 124001 [Google Scholar]
- Klioner, S. A., & Kopeikin, S. M. 1992, AJ, 104, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Klioner, S. A., & Mignard, F. M. 2014a, Recommended initial precession phase for Gaia Scanning Law, Tech. rep., GAIA-C3-TN-TUD-SK-018-1 [Google Scholar]
- Klioner, S. A. & Mignard, F. M. 2014b, Recommended initial spin phase for Gaia Scanning Law for the period until 31.12.2015, Tech. rep., GAIA-C3-TN-LOSK-022-1 [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [Google Scholar]
- Lattanzi, M. G., Bucciarelli, B., Holfeltz, S. T., & Taff, L. G. 1993, in Developments in Astrometry and their Impact on Astrophysics and Geodynamics, eds. I. I. Mueller & B. Kolaczek, 156, 47 [NASA ADS] [Google Scholar]
- Lindegren, L., Lammers, U., Hobbs, D., et al. 2012, A&A, 538, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Reback, J., Jbrockmendel, McKinney, W., et al. 2021, https://doi.org/10.5281/zenodo.5060318 [Google Scholar]
- Treuhaft, R. N., & Lowe, S. T. 1991, AJ, 102, 1879 [CrossRef] [Google Scholar]
- van Altena, W., Anderson, J., Benedict, G. F., et al. 2013, Astrometry for Astrophysics (Cambridge University Press) [Google Scholar]
- Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]
- Whipple, A. L., Jefferys, W. H., Benedict, G. F., et al. 1996, in Bulletin of the American Astronomical Society, AAS/Division of Dynamical Astronomy Meeting #27, 28, 1187 [Google Scholar]
A frame is given by the observations of stars over one transit where these observations are obtained with the AF1-9 CCD column fiducial lines; tij, which can be obtained with any given CCD column, lies within Δt =40 s from the target star observing time for the same column. Then the AL-AC rate is used to transform tij for that transit to the target stars’ observing time at AF5.
Sources brighter than G ~ 12 lead to saturated images mainly due to the sensitivity of the astrometric instrument. TDI gates mitigate this effect; they are special structures on the CCDs that can be activated in order to inhibit charge transfer and hence to effectively reduce the integration time for bright sources.
All Tables
All Figures
 |
Fig. 1 CCD pair scan AL rates for transit number 1. The green and magenta points show the pair scan rates for FOV1 and FOV2, respectively, while the rate medians obtained in bins of 0.5 s for these measurements is shown by the orange line that connects each point separated by 1 s. The black dashed line shows the AL rate, as obtained with OGA3.2 (including the corrective attitude), at the same times as for the orange line. |
| In the text | |
 |
Fig. 2 Scene around the target star successfully detected onboard during the transit on 2017-02-22T19:08:12.954 (UTC) at a predicted angular distance of 67.65j from Jupiter’s limb. We note the gap between the detectors in CCD rows 6 and 7. Whilst Jupiter was observed in row 6, the target star happened to be scanned in row 7. Image credit: ESA/Gaia/DPAC/C. Crowley. |
| In the text | |
 |
Fig. 3 Star field surrounding the brightest star closest to Jupiter’s limb in the magnitude range of 10 < G < 13 mag within o.8 × 1.3 deg on the sky along with Jupiter using the INPOP10 ephemeris. The small green star symbols show the stars, the big red dots denote Jupiter’s position as seen on each transit by Gaia when the target star was observed (the single large red dot on the left is the January transit, and the set of 25 dots in the center are the February transits), and the target star is shown as the large blue star at α = 201.41, δ = −7.38 deg. |
| In the text | |
 |
Fig. 4 AL coordinate for the target star, |
| In the text | |
 |
Fig. 5 Zoom-in on the highest deflection observed at the third transit shown in Fig. 4, with the observations being depicted as blue circles and the predicted AL-light deflection by Jupiter as the red line. The numbers accompanying each blue circle denote the corresponding AF column associated with the observation, e.g., 1 means that the measurement is associated with AF1. It can be seen that the AF1 measurement is an outlier at more than 3-σ. |
| In the text | |
 |
Fig. 6 Joint AL-AC post-fit residual distribution of the reference stars in the first 15 transits of the GAREQ field (further described in the main text) surrounding the target star and showing σAL = 180 μas and σAC = 1.822 mas. The red shaded ellipse shows the 1σ joint uncertainty. The histogram distributions are shown in the margins: AL is at the top and AC is on the right. |
| In the text | |
 |
Fig. 7 Joint AL-AC post-fit residual distribution of the reference stars in the last 10 transits of the GAREQ field (further described in the main text) surrounding the target star and showing σAL = 162 μas and σAC = 1.469 mas, which is depicted as the red shaded ellipse in the form of the 1-σ joint uncertainty. The corresponding AL and AC histogram residual distributions are shown in the margins. |
| In the text | |
 |
Fig. 8 Post-fit AL (panel a) and AC (panel b) residuals of the reference stars in the 15 transits versus the magnitude of the star. The color coding is as a function of the AL-AC residual value. |
| In the text | |
 |
Fig. 9 Joint AL-AC post-fit residual distribution of stars in a “quiet” field showing σAL = 150 μas and σAC = 1.213 mas, depicted as the red shaded ellipse in the form of the 1-σ joint uncertainty. The corresponding histogram distributions are shown in the margins. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.