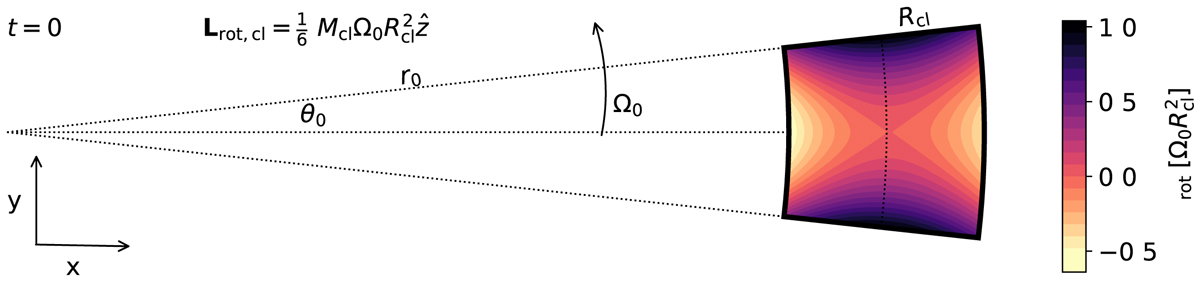
Schematic setup of our analytical calculation (Sect. 2). We consider a two-dimensional cloud of mass M_cl in a stationary frame, whose origin lies on the central mass M_C ≫ M_cl (where the dotted lines cross). The initial shape of the cloud is that of a partial annulus, bounded by inner and outer circles with radii r₀ ± R_cl and radial lines at angles ±θ₀. We follow the position and velocity of the cloud’s center-of-mass over time and calculate the specific rotational angular momentum of cloud particles relative to this point as , shown in the color plot at t = 0. The initial velocities of the cloud particles correspond to circular, Keplerian motion. Particles that start on the x-axis initially contribute retrograde rotation due to shear, whereas particles on the y-axis contribute prograde rotation due to curvature. The integrated result is a net initial prograde rotational angular momentum that increases over time if the cloud orbits freely (see Eq. (14b)).