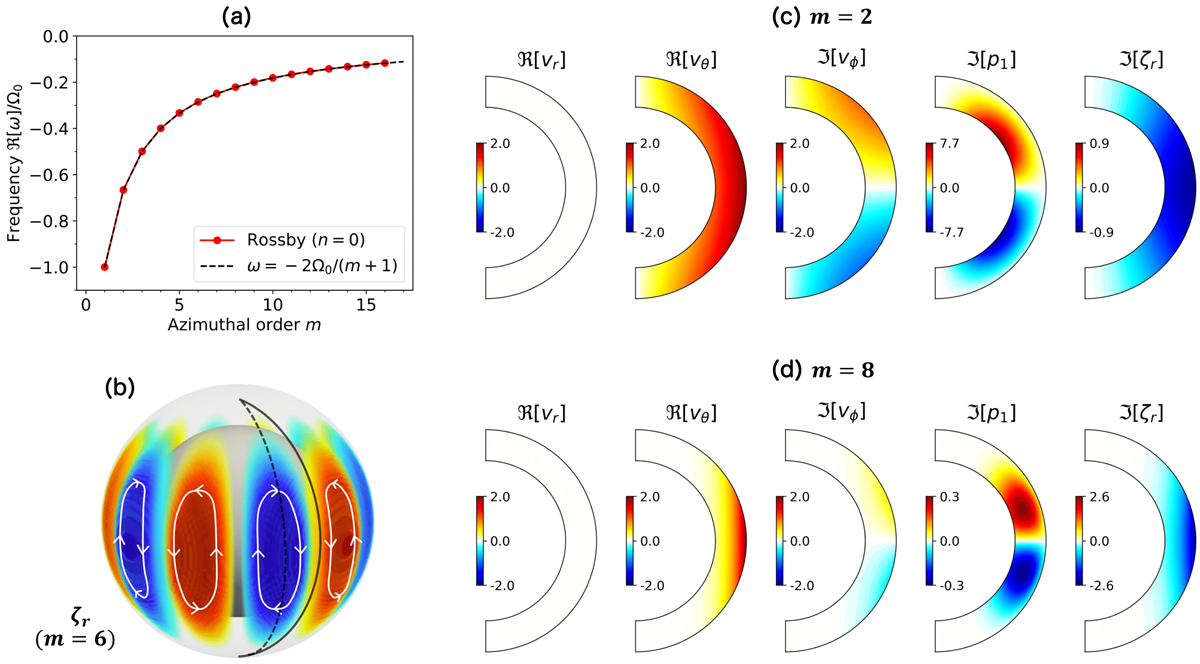
Dispersion relation and eigenfunctions of the equatorial Rossby modes without radial nodes in the case of uniform rotation, no viscosity, and adiabatic stratification. (a) Dispersion relation from the calculated modes (red). Overplotted black dashed line represents the theoretical dispersion relation of the sectoral (l = m) Rossby modes ω = 2Ω₀/(m + 1). (b) Schematic illustration of flow structure of the mode with m = 6. The red and blue volume rendering shows the structure of ℜ[ζ_r(r, θ)exp(imϕ − iωt)]. The black solid curve shows the meridional plane at ϕ = 0 and at t = 0 where v_r and v_θ are purely real and v_ϕ, p₁, and ζ_r are purely imaginary. The black dashed line denotes the meridional plane at ϕ = −π/2m where v_ϕ, p₁ and ζ_r are real. (c) Meridional cuts of the m = 2 eigenfunctions for the velocity v(r, θ)exp[i(mϕ − ωt)], the pressure p₁(r, θ)exp[i(mϕ − ωt)], and the radial vorticity ζ_r(r, θ)exp[i(mϕ − ωt)]. The solutions are shown in the meridional plane at ϕ = 0 and t = 0. The units of the color bars are m s⁻¹ for the three velocity components, 10⁵ dyn cm⁻² for the pressure, and 10⁻⁸ s⁻¹ for the vorticity. The eigenfunctions are normalized such that the maximum of |v_θ| is 2 m s⁻¹. (d) The same as panel c but for m = 8.